ソーティングアルゴリズムの性能
「本当に実用的なたったひとつのソートアルゴリズム」
という記事に感化され、思わずソートアルゴリズムの復習。
1から50000までの乱数を1万個の配列に格納し、
「挿入ソート」「クイックソート」「マージソート」「基数ソート」「鳩ノ巣ソート」
のうち、どのソートの処理速度が速いのかを調べてみました。
ちなみにプログラムはDelphi2007で作成。
(ネットにはC++のコードサンプルが多く、これらをDelphiで焼き直しました。)
測定タイマーは1/1000秒単位まで計測できるように調整しています。
今回作成したソートプログラムのプログラムソースは以下の通り。
(※半角スペースを全角スペースに置換しています。)
const
c_num = 10000;
c_max = 50000;
//*********************************************************************
// 挿入ソート
//---------------------------------------------------------------------
// IntArray : ソートする配列
// Count : 要素数
//*********************************************************************
Procedure TForm7.InsSort(var iArray: array of integer; const Count: integer);
var i, j: integer;
temp: integer;
begin
for i := 1 to Count-1 do
begin
j := i;
temp := iArray[j];
while (j > 0) and (temp < iArray[j-1]) do
begin
iArray[j] := iArray[j-1];
dec(j);
end;
iArray[j] := temp;
end;
end;
//*********************************************************************
// クイックソート
//---------------------------------------------------------------------
// first, last : 先頭、最終
// iArray : ソートする配列
//*********************************************************************
procedure TForm7.quicksort(first, last: integer; var iArray: array of integer);
var
l, r, pivot: integer;
procedure swap(var larray: array of integer; first, last: integer);
var
temp: integer;
begin
temp := larray[first];
larray[first] := larray[last];
larray[last] := temp;
end;
begin
if (last > first) then
begin
l := first;
r := last;
pivot := iArray[(last + first) div 2];
while (l < r) do
begin
while iArray[l] < pivot do
l := l + 1;
while iArray[r] > pivot do
r := r - 1;
if (l <= r) then
begin
swap(iArray, l, r);
l := l + 1;
r := r - 1;
end;
end;
if (first < r) then
quicksort(first, r, iArray);
if (last > l) then
quicksort(l, last, iArray);
end;
end;
//*********************************************************************
// マージソート
//---------------------------------------------------------------------
// iArray : ソートする配列
// F, L : 先頭、最終
//*********************************************************************
procedure TForm7.Mergesort(var iArray : array of integer; F,L : integer);
Procedure Merge(var iArray : array of integer; F,Mid,L : integer);
var
Temparray : array[1..c_num] of integer;
First1,Last1,First2,last2,Index : integer;
begin
First1 := F;
Last1 := Mid;
First2 := Succ(Mid);
last2 := L;
Index := First1;
while ((First1 <= Last1) and (First2 <= Last2)) do
begin
if iArray[First1] < iArray[First2] then
begin
Temparray[Index] := iArray[First1];
First1 := succ(First1);
Index := succ(Index);
end else
begin
Temparray[Index] := iArray[First2];
First2 := succ(First2);
Index := succ(Index);
end;
end;
while (First1 <= Last1) do
begin
Temparray[Index] := iArray[First1];
First1 := succ(First1);
Index := succ(Index);
end;
while (First2 <= Last2) do
begin
Temparray[Index] := iArray[First2];
First2 := succ(First2);
Index := succ(Index);
end;
for Index := F to L do
iArray[Index] := Temparray[Index];
end;
var
Mid : integer;
begin
if F < L then
begin
Mid := (F + L) div 2;
Mergesort(iArray,F,Mid);
Mergesort(iArray,Mid+1,L);
Merge(iArray,F,Mid,L);
end;
end;
//*********************************************************************
// 基数ソート
//---------------------------------------------------------------------
// iArray : ソートする配列
// n : データの数
// r : 基数を取り出す最大値
//*********************************************************************
procedure TForm7.RadixSort(var iArray : array of integer; n,r : integer);
var
i, j, k, m : Integer;
Buffarray : array[1..c_num] of integer;
Temparray : array[1..c_num] of integer;
begin
m := 1;
while (m <= r) do
begin
for i := 0 to (n-1) do
begin
Buffarray[i] := (iArray[i] div m) mod 10;
end;
k := 0;
for i := 0 to 9 do
begin
for j := 0 to (n-1) do
begin
if (Buffarray[j] = i) then
begin
Inc(k);
Temparray[k] := iArray[j];
end;
end;
end;
for i := 0 to (n-1) do
begin
iArray[i] := Temparray[i];
end;
m := m * 10;
end;
end;
//*********************************************************************
// 鳩ノ巣ソート
//---------------------------------------------------------------------
// iArray : ソートする配列
// num : データの数
// min : 最小値
// max : 最大値
//*********************************************************************
procedure TForm7.PigeonholeSort(var iArray : array of integer; num,min,max : integer);
var
size,i,j,k,count : Integer;
holes: array [0..c_max] of Integer;
hc : Integer;
v : Integer;
begin
size := max - min + 1;
for i := 0 to size-1 do
begin
holes[i] := 0;
end;
for j := 0 to num-1 do
begin
v := iArray[j] - min;
holes[v] := holes[v] + 1;
end;
k := 0;
for count := 0 to size-1 do
begin
hc := holes[count];
while hc>0 do
begin
hc := holes[count];
hc := hc - 1;
holes[count] := hc;
iArray[k] := count + min;
Inc(k);
end;
end;
end;
ソート比較のまとめ
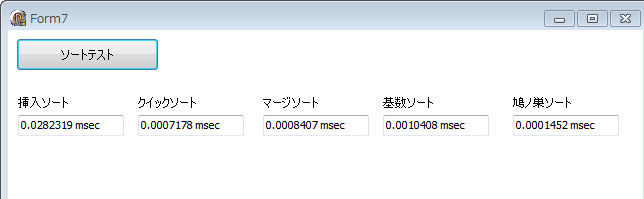 <
<やはりというか、1万個の配列で試したこともあり、
鳩ノ巣ソートが圧倒的に速いようです。
意外にもマージソートも速かったのには驚きです。
ということで、今回の調査では、
1位:鳩ノ巣ソート
2位:クイックソート
3位:マージソート
4位:基数ソート
5位:挿入ソート
の順位となりました。
「本当に実用的なたったひとつのソートアルゴリズム」
にあった、現実世界(トランプを使った)でのソート結果とは異なることがわかります。
「挿入ソート」「クイックソート」「マージソート」「基数ソート」「鳩ノ巣ソート」
は日本語での呼び方ですが、
英語表記では、
Insert Sort、Quick Sort、Merge Sort、Radix Sort、Pigeonhole Sortとなります。
今回は掲載しませんが、
C++やPython、Javaなどのコードサンプルが必要な場合は、
上記の英語表記で検索すると良いかと思います。
あくまで、手作業によるソートと、コンピュータによるソートを比較した場合、
結果が異なるということの証明にもなった気がします。
ソート繋がりでいうと、
常識を覆すソートアルゴリズム!その名も"sleep sort"!
ってのが話題になった時期もありました。
また、今回はソートのアルゴリズムの解説はしませんでしたので、
知りたい方は、
定番アルゴリズムを徹底理解!
なんかがお勧めです。
【このカテゴリーの最新記事】
- no image
- no image








