Important: the methods presented here
are suitable for assessing monotonic trends
(i.e. data without seasonality)
in discrete data
(i.e. not floating point). Additionally, if you apply the
methods in this tutorial to new data (i.e. region, time frame, source) you may
need to adjust the min
and max
visualization parameters to suit the
particular results.
Time series data
We will use a time series of MODIS Enhanced Vegetation Index (EVI) from the MOD13A1 dataset. Each pixel of this image collection contains a time series and we will compute the stats in each pixel. Assume that filtering the collection to one season is sufficient to obtain time series with monotonic trends. To check the validity of that assumption for your area of interest, add the collection to the map and using the inspector, click some points and view the series chart presented in the console. Adjust the filter as necessary.
var
mod13
=
ee
.
ImageCollection
(
'MODIS/006/MOD13A1'
);
var
coll
=
mod13
.
select
(
'EVI'
)
.
filter
(
ee
.
Filter
.
calendarRange
(
8
,
9
,
'month'
));
Map
.
setCenter
(
-
121.6
,
37.3
,
10
);
Map
.
addLayer
(
coll
,
{
min
:
-
500
,
max
:
5000
,
palette
:
[
'white'
,
'green'
]},
'coll'
);
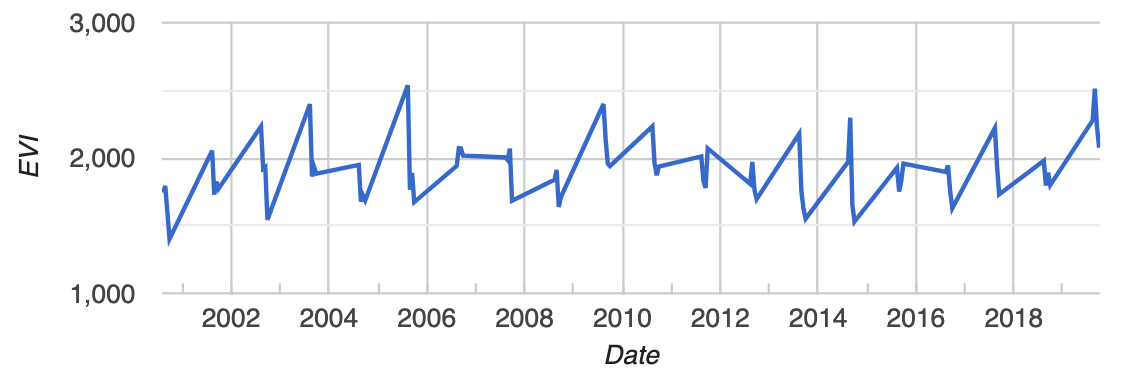
An example EVI time series (one pixel) from this collection is shown below. Is there a trend in this pixel? More importantly, is a there a statistically significant trend in this pixel? Read on to find out!
Join the time series to itself
The non-parametric stats of interest are computed by examining every possible
ordered pair of unique values in the time series. If there are n
time points
in the series, we need to examine the n(n-1)/2
pairs (i, j)
, i<j
, where i
and j
are arbitrary time indices. (Here we use (i, j)
to signify the
pair of EVI images indexed by i
and j
). To do that, join the collection to
itself with a temporal filter. The temporal filter will pass all the
chronologically later images. In the joined collection, each image will
store all the images that come after it in an after
property.
var
afterFilter
=
ee
.
Filter
.
lessThan
({
leftField
:
'system:time_start'
,
rightField
:
'system:time_start'
});
var
joined
=
ee
.
ImageCollection
(
ee
.
Join
.
saveAll
(
'after'
).
apply
({
primary
:
coll
,
secondary
:
coll
,
condition
:
afterFilter
}));
Mann-Kendall trend test
The Mann-Kendall trend is defined as the sum of the signs of all the pairs.
The sign
is 1 if EVI at time j
is more than EVI at time i
, -1 if the
opposite is true and zero otherwise (if they're equal). Compute this by
iterating over the collection and computing sign(i, j)
for each image i
in the collection and each image j
in the after
images.
var
sign
=
function
(
i
,
j
)
{
// i and j are images
return
ee
.
Image
(
j
).
neq
(
i
)
// Zero case
.
multiply
(
ee
.
Image
(
j
).
subtract
(
i
).
clamp
(
-
1
,
1
)).
int
();
};
var
kendall
=
ee
.
ImageCollection
(
joined
.
map
(
function
(
current
)
{
var
afterCollection
=
ee
.
ImageCollection
.
fromImages
(
current
.
get
(
'after'
));
return
afterCollection
.
map
(
function
(
image
)
{
// The unmask is to prevent accumulation of masked pixels that
// result from the undefined case of when either current or image
// is masked. It won't affect the sum, since it's unmasked to zero.
return
ee
.
Image
(
sign
(
current
,
image
)).
unmask
(
0
);
});
// Set parallelScale to avoid User memory limit exceeded.
}).
flatten
()).
reduce
(
'sum'
,
2
);
var
palette
=
[
'red'
,
'white'
,
'green'
];
// Set min and max stretch visualization parameters as necessary.
Map
.
addLayer
(
kendall
,
{
palette
:
palette
,
min
:
-
2800
,
max
:
2800
},
'kendall'
);
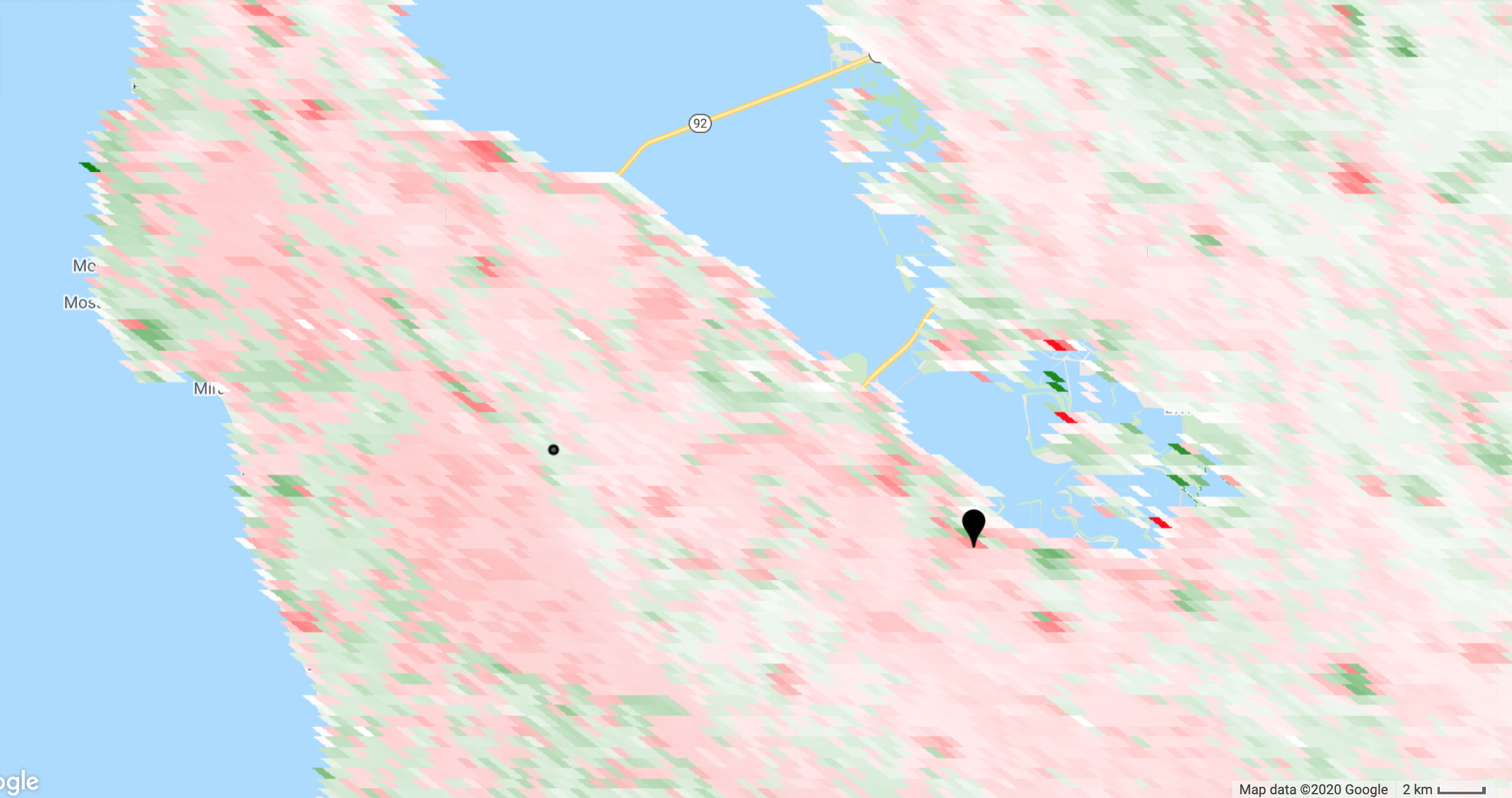
Zoom to your area of interest and define a roughly symmetric color stretch
using the map layers styling dialog (i.e. the mean of min
and max
should
be approximately zero). The red pixels are decreasing trend and the green
pixels are increasing trend. This is illustrated in the following image of
the Mann-Kendall statistic for an area of California, USA. The map pin is
at the approximate location of the Googleplex. The dot is the location of
the point from which the time series shown above was extracted. We'd like
to identify which pixels in this map have significant trend.
You may also be interested in knowing the magnitude of the trend, or the slope of the trend over time in the present context. A non-parametric way of assessing that is with Sen's slope.
Sen's slope
Sen's slope is computed in a similar way to the Mann-Kendall statistic. However, instead of adding all the signs of the pairs, the slope is computed for all the pairs. Sen's slope is the median slope from all those pairs. In the following, slope is computed over days to avoid numerically tiny slopes (which might result from using epoch time instead).
var
slope
=
function
(
i
,
j
)
{
// i and j are images
return
ee
.
Image
(
j
).
subtract
(
i
)
.
divide
(
ee
.
Image
(
j
).
date
().
difference
(
ee
.
Image
(
i
).
date
(),
'days'
))
.
rename
(
'slope'
)
.
float
();
};
var
slopes
=
ee
.
ImageCollection
(
joined
.
map
(
function
(
current
)
{
var
afterCollection
=
ee
.
ImageCollection
.
fromImages
(
current
.
get
(
'after'
));
return
afterCollection
.
map
(
function
(
image
)
{
return
ee
.
Image
(
slope
(
current
,
image
));
});
}).
flatten
());
var
sensSlope
=
slopes
.
reduce
(
ee
.
Reducer
.
median
(),
2
);
// Set parallelScale.
Map
.
addLayer
(
sensSlope
,
{
palette
:
palette
,
min
:
-
1
,
max
:
1
},
'sensSlope'
);
To get Sen's intercept (if you need it), compute all intercepts and take the median.
var
epochDate
=
ee
.
Date
(
'1970-01-01'
);
var
sensIntercept
=
coll
.
map
(
function
(
image
)
{
var
epochDays
=
image
.
date
().
difference
(
epochDate
,
'days'
).
float
();
return
image
.
subtract
(
sensSlope
.
multiply
(
epochDays
)).
float
();
}).
reduce
(
ee
.
Reducer
.
median
(),
2
);
Map
.
addLayer
(
sensIntercept
,
{
min
:
-
6600
,
max
:
20600
},
'sensIntercept'
);
A map of Sen's slope is shown below. Note that the pattern is similar to the Mann-Kendall statistic, but not identical. Also, there is still the question of which pixels have significant trend, a question that will be answered shortly.
The previous examples are only to demonstrate the computation. If you need Sen's slope and/or intercept, you can also use the Sen's slope reducer which is likely to be easier (less code) and more efficient, but computes the intercept as the y-value of the line that passes through the medians.
Variance of the Mann-Kendall statistic
Computing the variance of the Mann-Kendall statistic is complicated by the
possible presence of ties in the data (i.e. sign(i, j)
equals zero).
Counting those ties can get a little dicey, requiring an array-based
forward differencing. Note that you can comment .subtract(groupFactorSum)
in the computation of kendallVariance
if you don't care about ties and
want to disregard that correction.
// Values that are in a group (ties). Set all else to zero.
var
groups
=
coll
.
map
(
function
(
i
)
{
var
matches
=
coll
.
map
(
function
(
j
)
{
return
i
.
eq
(
j
);
// i and j are images.
}).
sum
();
return
i
.
multiply
(
matches
.
gt
(
1
));
});
// Compute tie group sizes in a sequence. The first group is discarded.
var
group
=
function
(
array
)
{
var
length
=
array
.
arrayLength
(
0
);
// Array of indices. These are 1-indexed.
var
indices
=
ee
.
Image
([
1
])
.
arrayRepeat
(
0
,
length
)
.
arrayAccum
(
0
,
ee
.
Reducer
.
sum
())
.
toArray
(
1
);
var
sorted
=
array
.
arraySort
();
var
left
=
sorted
.
arraySlice
(
0
,
1
);
var
right
=
sorted
.
arraySlice
(
0
,
0
,
-
1
);
// Indices of the end of runs.
var
mask
=
left
.
neq
(
right
)
// Always keep the last index, the end of the sequence.
.
arrayCat
(
ee
.
Image
(
ee
.
Array
([[
1
]])),
0
);
var
runIndices
=
indices
.
arrayMask
(
mask
);
// Subtract the indices to get run lengths.
var
groupSizes
=
runIndices
.
arraySlice
(
0
,
1
)
.
subtract
(
runIndices
.
arraySlice
(
0
,
0
,
-
1
));
return
groupSizes
;
};
// See equation 2.6 in Sen (1968).
var
factors
=
function
(
image
)
{
return
image
.
expression
(
'b() * (b() - 1) * (b() * 2 + 5)'
);
};
var
groupSizes
=
group
(
groups
.
toArray
());
var
groupFactors
=
factors
(
groupSizes
);
var
groupFactorSum
=
groupFactors
.
arrayReduce
(
'sum'
,
[
0
])
.
arrayGet
([
0
,
0
]);
var
count
=
joined
.
count
();
var
kendallVariance
=
factors
(
count
)
.
subtract
(
groupFactorSum
)
.
divide
(
18
)
.
float
();
Map
.
addLayer
(
kendallVariance
,
{
min
:
1700
,
max
:
85000
},
'kendallVariance'
);
Significance testing
The Mann-Kendall statistic is asymptotically normal for suitably large
samples. Assume our samples are suitably large and uncorrelated. Under these
assumptions, the true mean of the Mann-Kendall statistic is zero and the
variance is as computed above. To compute a standard normal statistic ( z
),
divide the statistic by its standard deviation. The P-value of the z-statistic
(probability of observing such an extreme value) is 1 - P(|z| < Z)
. For
a two-sided test of whether any trend exists (positive or negative) at the
95% confidence level, compare the P-value to 0.975. (Alternatively, compare
the z-statistic to Z*
, where Z*
is the inverse distribution function
of 0.975).
The standard normal distribution function can be computed in Earth Engine from
the error function, erf()
. Both the distribution function and its inverse
are shown below for reference. Here we use the distribution function to get 1 - P(|z| < Z)
and compare it to 0.975.
// Compute Z-statistics.
var
zero
=
kendall
.
multiply
(
kendall
.
eq
(
0
));
var
pos
=
kendall
.
multiply
(
kendall
.
gt
(
0
)).
subtract
(
1
);
var
neg
=
kendall
.
multiply
(
kendall
.
lt
(
0
)).
add
(
1
);
var
z
=
zero
.
add
(
pos
.
divide
(
kendallVariance
.
sqrt
()))
.
add
(
neg
.
divide
(
kendallVariance
.
sqrt
()));
Map
.
addLayer
(
z
,
{
min
:
-
2
,
max
:
2
},
'z'
);
// https://en.wikipedia.org/wiki/Error_function#Cumulative_distribution_function
function
eeCdf
(
z
)
{
return
ee
.
Image
(
0.5
)
.
multiply
(
ee
.
Image
(
1
).
add
(
ee
.
Image
(
z
).
divide
(
ee
.
Image
(
2
).
sqrt
()).
erf
()));
}
function
invCdf
(
p
)
{
return
ee
.
Image
(
2
).
sqrt
()
.
multiply
(
ee
.
Image
(
p
).
multiply
(
2
).
subtract
(
1
).
erfInv
());
}
// Compute P-values.
var
p
=
ee
.
Image
(
1
).
subtract
(
eeCdf
(
z
.
abs
()));
Map
.
addLayer
(
p
,
{
min
:
0
,
max
:
1
},
'p'
);
// Pixels that can have the null hypothesis (there is no trend) rejected.
// Specifically, if the true trend is zero, there would be less than 5%
// chance of randomly obtaining the observed result (that there is a trend).
Map
.
addLayer
(
p
.
lte
(
0.025
),
{
min
:
0
,
max
:
1
},
'significant trends'
);
The following shows a map of the "significant" pixels (in white), or the
pixels that pass the p.lte(0.025)
test. If our assumptions are correct
and you are satisfied with the computation, you may wish to treat these
pixels differently, by using p.lte(0.025)
as a mask. Note that the pixel
with the time series shown above (red in the map below) does NOT have a
significant trend.
Some call this process significance testing. Pixels that are "significant"
satisfy the condition that p.lte(0.025)
and are assumed to have a real
trend. Other pixels are assumed to not have a trend and are removed from
further analysis. Some consider this process cultish
( Ziliak and McCloskey 2009
).
You decide!
References
- Thiel. 1950. A rank-invariant method of linear and polynomial regression analysis.
- Sen. 1968. Estimates of the Regression Coefficient Based on Kendall's Tau
- Morell and Fried 2009. On Nonparametric Tests for Trend Detection in Seasonal Time Series
- Pohlert 2020. Non-Parametric Trend Tests and Change-Point Detection
