This unit focuses on different types of conditionsused to build decision trees.
Axis-aligned vs. oblique conditions
An axis-aligned conditioninvolves only a single feature. An oblique conditioninvolves multiple features. For example, the following is an axis-aligned condition:
num_legs ≥ 2
While the following is an oblique condition:
num_legs ≥ num_fingers
Often, decision trees are trained with only axis-aligned conditions. However, oblique splits are more powerful because they can express more complex patterns. Oblique splits sometime produce better results at the expense of higher training and inference costs.
split_axis="SPARSE_OBLIQUE"
parameter.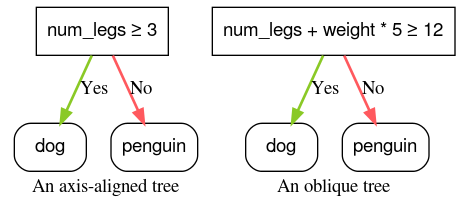 = 3". The oblique condition is
"num_legs + weight * 5 >= 12". " title="image_tooltip" class="p_maxWidth"/>
= 3". The oblique condition is
"num_legs + weight * 5 >= 12". " title="image_tooltip" class="p_maxWidth"/>
Figure 4. Examples of an axis-aligned condition and an oblique condition.
Graphing the preceding two conditions yields the following feature space separation:
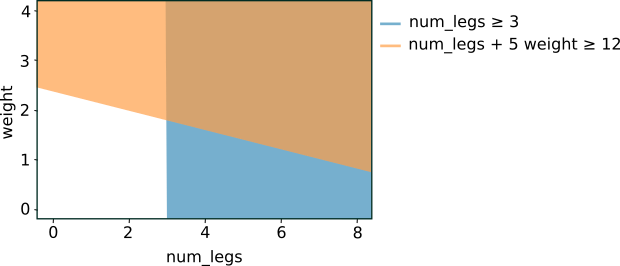
Figure 5. Feature space separation for the conditions in Figure 4.
Binary vs. non-binary conditions
Conditions with two possible outcomes (for example, true or false) are called binary conditions. Decision trees containing only binary conditions are called binary decision trees.
Non-binary conditionshave more than two possible outcomes. Therefore, non-binary conditions have more discriminative power than binary conditions. Decisions containing one or more non-binary conditions are called non-binary decision trees.
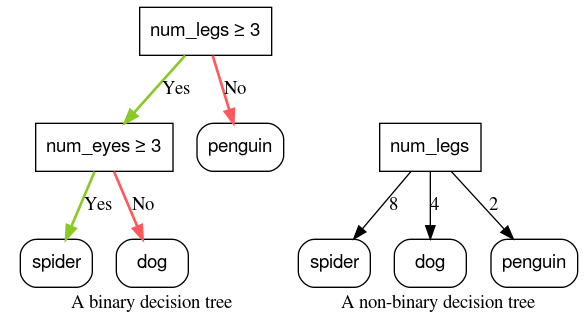
Figure 6: Binary versus non-binary decision trees.
Conditions with too much power are also more likely to overfit. For this reason, decision forests generally use binary decision trees, so this course will focus on them.
The most common type of condition is the threshold conditionexpressed as:
feature
≥ threshold
For example:
num_legs ≥ 2
Other types of conditions exist. Following are other commonly used types of binary conditions:
Table 2. Common types of binary conditions.
| Name | Condition | Example |
| threshold condition | $\mathrm{feature}_i \geq \mathrm{threshold}$ | $\mathrm{num\_legs} \geq 2$ |
| equality condition | $\mathrm{feature}_i = \mathrm{value}$ | $\mathrm{species} = ``cat"$ |
| in-set condition | $\mathrm{feature}_i \in \mathrm{collection}$ | $\mathrm{species} \in \{``cat", ``dog", ``bird"\}$ |
| oblique condition | $\sum_{i} \mathrm{weight}_i \mathrm{feature}_i \geq \mathrm{threshold}$ | $5 \ \mathrm{num\_legs} + 2 \ \mathrm{num\_eyes} \geq 10$ |
| feature is missing | $\mathrm{feature}_i \mathrm{is} \mathrm{Missing}$ | $\mathrm{num\_legs} \mathrm{is} \mathrm{Missing}$ |

