漸化式で解くコンデンサー回路
漸化式で解くコンデンサー回路@スイッチ連続操作<問題>
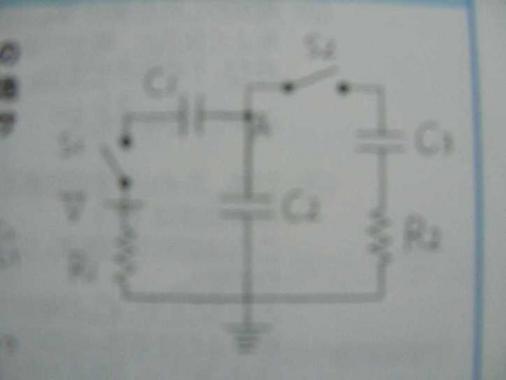
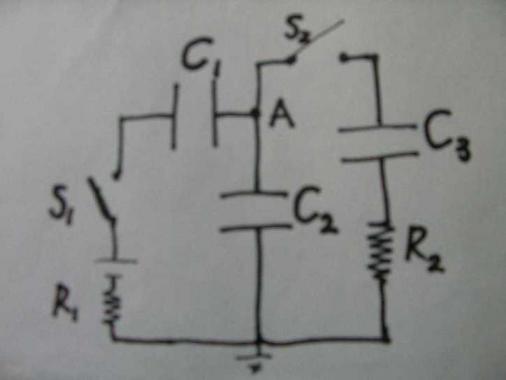
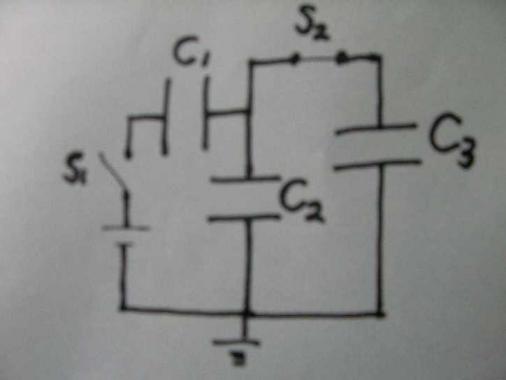
(下の図は問題の図を書き直したものです)
図中の記号はそれぞれ
S1、S2はスイッチ、
C1、C2、C3はそれぞれ電気容量が
C1=C[F]
C2=2C[F]
C3=4C[F]
のコンデンサー、
Rは抵抗、
Vは電池の電圧(起電力)。
を表している。
このような電気回路において
以下の手順で
スイッチ切り替え操作を行う。
まずS1、S2が開いている状態から出発して
a.スイッチ1(S1)を閉じる
↓(十分時間がたってから)
b.S1を開き、スイッチ2(S2)を閉じる
↓(十分時間がたってから)
c.S2を開き、S1を閉じる
↓(十分時間がたってから)
d.S1を開き、S2を閉じる
↓(以下、繰り返し)
このようなスイッチ切り替えを繰り返ていくと
いずれ
スイッチを切り替えても
電荷の移動が起こらなくなってしまう(定常状態になる)
そのときの、点Aにおける電位V∞はいくらになるか?
<問題文終>
(出典:わ●わく物理●検隊)← 高校物理の参考書です。
<準備>

まず、十分時間が経過してコンデンサーが充電されると
電流が流れていない状態(=抵抗の電圧ゼロ)になっているので
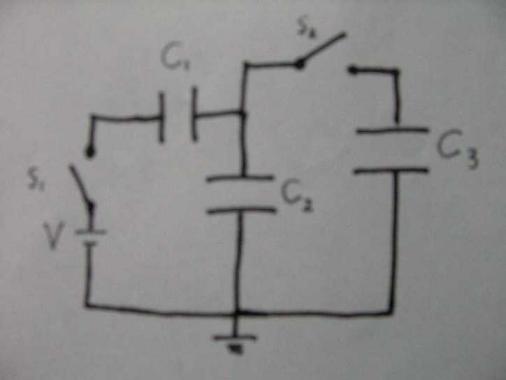
抵抗を省き
道線に直した回路に書き換える。(以下、この回路を元に考察しています。)
スイッチ切り替えのカウントは
スイッチ1、2
共に開いている状態からスタート
して

↓
(a)スイッチ1を閉じる。(スイッチ2は開いている)
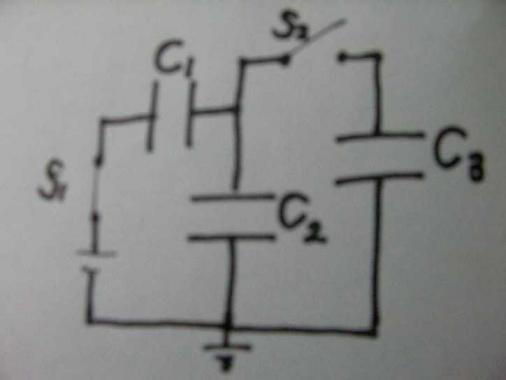
↓
十分に時間がたってから
(b)スイッチ1を開き、スイッチ2を閉じる
↓
十分に時間がたってから( ここで1回カウント
)
(c)スイッチ2を開き、スイッチ1を閉じる

↓
十分に時間がたってから
(d)スイッチ1を開き、スイッチ2を閉じる

↓
十分に時間がたってから( ここで1回カウント
)
・
・ (以下無限ループ)
・
以上のように計りました。
ここで
「n回目」から「n+1回目」の
電荷の流れを探るために
スイッチ2を閉じて十分に時間がたった状態

に至ってからを
1回の作業とカウント
さらに
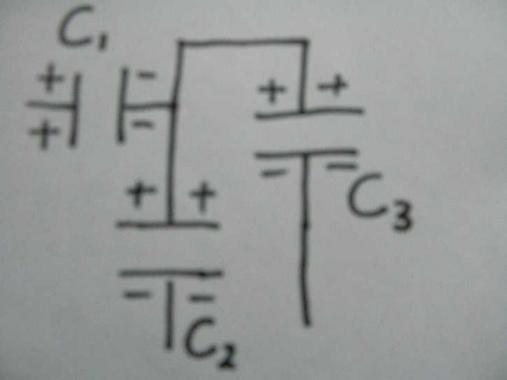
↑電荷が溜まっていく時の符号の様子
を上図のように仮定して考察を開始します。
<考察>
まず n回目
を終えた状態について。
一連の切り替えをn回終え十分に時間がたったあと
の
コンデンサーに囲まれた
孤立部分の点Aの電位を Vn
とすると
孤立部分点Aとアースとの電圧がVnになるということだから
コンデンサーの電気量の関係式Q=CV
C1=C[F]
C2=2C[F]
C3=4C[F]より
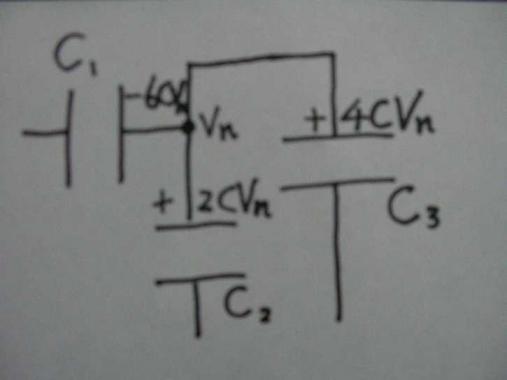
C3
には
Q3n=+C3Vn= +4CVn
C2
には
Q2n=+C2Vn= +2CVn
だけの電荷がそれぞれ蓄えられることになる。
残り、C1に蓄えられる電荷ついて。
このとき(n回目測定時)スイッチ1は開いていて
電池と接続されていない状態で
C1の電荷は身動きが取れない(移動できない)
が
孤立部分の電荷量は一定だから
電荷の保存より、はじめの状態との保存式を作る。
左辺:電気的に孤立した部分の電気量(電荷)の総和
=右辺:始め(0回目)孤立部分の電荷も0だった状態
として
Q1n+Q2n+Q3n=0
-Q1n=+Q2n+Q3n
よって
C1に蓄えられる電荷は
-Q1n=+Q2n+Q3n= -6CVn
となる。
このあと、S2を開いてS1を閉じると
(n回目→n+1回目の電荷の流れを探っているので)
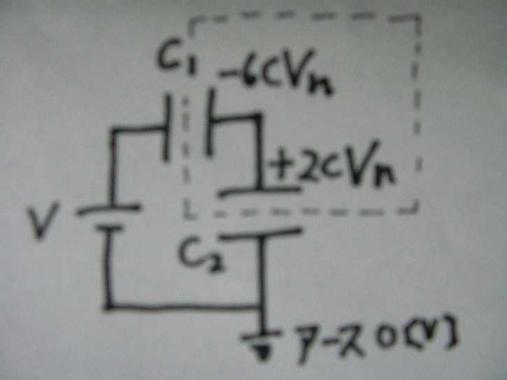
↑のようなC1、C2の閉回路となる。
はじめ、スイッチ1を閉じてスグの状態では
図のように
C1にQ1n=-6CVn
C2にQ2n=+2CVn
の電荷が溜まっているが
充電が完了する(十分に時間がたつ)頃には
C1、C2に溜まっている電荷も変わっている。
このときC1にX、C2にYだけの電荷が溜まるとすると
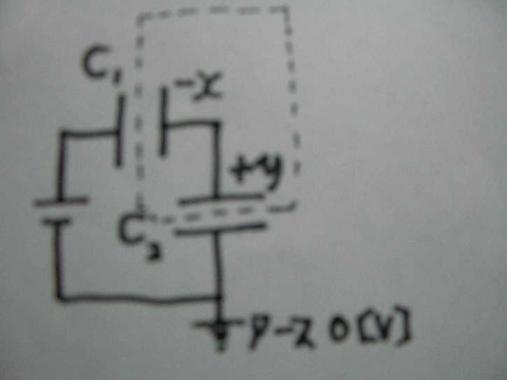
点線内の孤立部分では
C1にQ1n'=-X
C2にQ2n'=+Y
だけの電荷が蓄えられることになるから
はじめ(スイッチを切り替えた直後)

=
あと(切り替え後、十分に時間がたった後)

の点線部内の電荷保存の式が立てられる。
式を作ってみると
はじめ(スイッチを切り替えた直後)=あと(十分に時間がたった後) より
Q1n+Q2n=Q1n'+Q2n'
-6CVn+2CVn=-X+Y
…(1)
あと(切り替えして十分に時間がたった時)の状態では電圧(電位差)もまた、
V1+V2=V(電池の電圧・起電力)
と変化しているので
Q=CV⇔V=Q/Cを用いて
V1=|Q1'|/C1=X/C
V2=Q2n'/C2=Y/2C
まとめて
X/C+Y/2C=V
…(2)
ここで
(2)の左辺を整理してまとめると
(2)= 2X+Y=2CV
…(2)'
-6CVn+2CVn=-X+Y
…(1)
2X+Y=2CV
…(2)'
(1)と(2)'式を連立方程式で解くと…
・Xについて
(1)-(2)'より
-3X=-4CVn-2CV (↓両辺×-1)
3X=2CV+4CVn (↓両辺×1/3)
X=2CV/3+4CVn/3
(↓2C/3で括るとき、4C/3=2×2C/3)
X=2C/3(V+2Vn)
↑まぁ結局…使うことはありませんでしたが^^;
・Yについて
(1)×2+(2)'より
3Y=-8CVn+2CV (↓両辺×1/3)
Y=2CV/3-8CVn/3
(↓2C/3で括るとき、8C/3=4×2C/3)
Y=2C/3(V-4Vn)
…(3)
以上のように電荷X,Yが求まる。
n+1回目
の電荷の流れについても調べておく。
今一度S1を開き、その後S2を閉じて
十分に時間がたった後(つまり n+1回目
)の
点Aの電位を Vn+1
とおき、
↓S2を閉じた直後
の
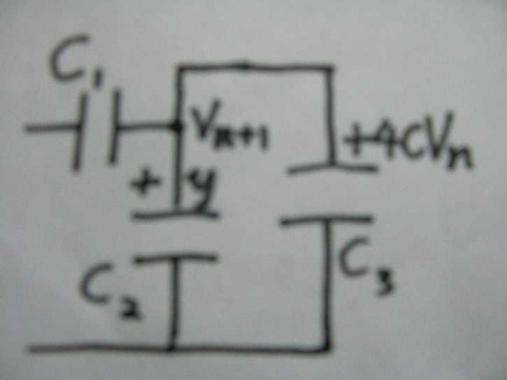
C2にQ2n'=+Y
C3にQn=CVn=+4CVn
の電荷が溜まっている状態と
(C1の電荷はS1を切っている事から例の如く移動できない)
↓S2を閉じて十分に時間がたったあと(n+1回目)
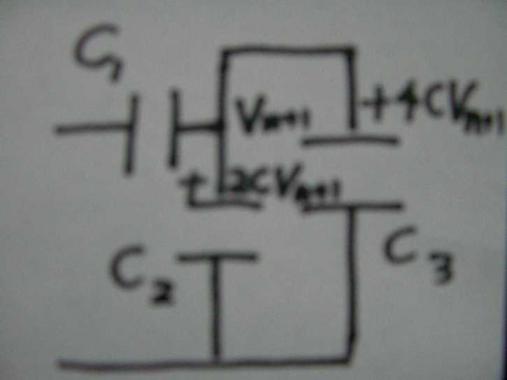
C2にQ2n+1=+2CVn+1
C3にQn+1=CVn+1=+4CVn+1
の電荷が溜まっている状態とを
電荷の保存式で結び付けてやれば
はじめの電荷量=あとの電荷量
Q2n'+Qn=Q2n+1+Qn
Y+4CVn=2CVn+1+4CVn+1
ここで(3)のYを代入して
2/3CV-8/3CVn+4CVn=2CVn+1+4CVn+1
6CVn+1=4CVn/3+2CV/3 (↓両辺×1/6C)
Vn+1=2Vn/9+1V/9
…(4)
という漸化式が完成!
この漸化式は
An+1=PAn+q型
An+1-K=P(An-K)の
特性方程式で処理するタイプだから
まず特性方程式
An+1-K=P(An-K)
を展開し整理して出てきた
An+1=PAn+(1-p)Kの係数(1-p)Kと
与式
An+1=PAn+qの定数qを比較して
(1-p)K=q
K=q/(1-p)
を調べ出す。
次に
Kを特性方程式に当てはめて
出てきた
An+1-q/(1-p)=P{An-q/(1-p)}
という式について
左辺An+1-q/(1-p)をBn+1とおけば
右辺An-q/(1-p)はBnとまとめることができる。
整理して
Bn+1=PBn
(An+1=rAn r=公比の等比数列型漸化式)
と表せば
Bn(An-q/(1-p)のこと)は
初項B1=A1-q/(1-p)
公比P
の 等比数列
であることが判明した。
あとはBnの等比数列を解いて
Bn=A1-q/(1-p)・(P)^n-1
Bn=An-q/(1-p)だったからまとめて
An-q/(1-p)=A1-q/(1-p)・(P)^n-1
An=A1-q/(1-p)・(P)^n-1+q/(1-p)
…といった具合に一般項を導くのだった。
Vn+1=2Vn/9+1V/9 …(4)も同様に
特性方程式と比較すると
Vn+1-K=2/9(Vn-K)
Vn+1=2Vn/9-2K/9+K
Vn+1=2Vn/9+7K/9
K=1V/7
Kを特性方程式に入れ整理すると
Vn+1-1V/7=2/9(Vn-V/7)
ここから
Vn-V/7=Bnと一塊にして考えると
Vn+1-1V/7=Bn+1とまとまるから
Bn+1=2Bn/9
Bn(Vn-V/7のこと)は
初項V1-V/7(整理して-2V/63 ※詳細は後述
)
公比2/9
の 等比数列
であることが分かる。
よって n回目における点Aの電位を表す式
は
Vn-V/7=-2V/63(2/9)^n-1
Vn=-2V/63(2/9)^n-1+V/7
-2V/63(2/9)^n-1について
-2V/63=-V/7*2/9と変形できるから
-2V/63(2/9)^n-1==-V/7*2/9*(2/9)^n-1
=-V/7(2/9)^n
Vn=-V/7(2/9)^n+V/7
…(5)
と求まった。
知りたいのは スイッチを切り替えても
電荷が移動しなくなるような点Aの電位
。
ある回数(例えばZ回目とする)で
電荷が流れなくなったとすると
以降は何度切り替えを繰り返しても電荷は移動しない。
電位もZ回目のまま以降は不変だから
n回目の電位の関係式(5)について極限を撮り
無限回繰り返したときの状態
を調べればいい。
よって
lim _[n→∞]Vn=-2V/63(2/9)^n-1+V/7
(lim _[n→∞]はnが無限大(∞)に近ずくということ)
ここで、公比=r=2/9は
分子より分母のほうが大きい分数
(-1<r<1)であるから
極限値lim _[n→∞]r^nにおいてnを増やしていくと
分母だけが巨大化していき、
どんどん0に近ずいていくので
∞付近では0に限りなく近くなる⇔0に収束すると扱う。
以上より、
無限大回切り替えを行ったときの点Aの電位
( 電荷が移動しなくなった回数以降の電位
)は
V∞=-V/7*0+V/7
V∞=V/7
であることが分かった!!!
※初項 (Vn-V/7)について
V1=1V/9を代入して
1V/9-V/7=-2V/63
※V1=1V/9の導出について。
はじめ(0回目)→1回目にかけての
電荷の流れを追う。
0回目からスタートしてS1を閉じ、S2が閉じてから
十分に時間がたった後の点Aの電位をVxとおいたとき
C1側には電池V、C2より下は
アースによって0Vになっているからそれぞれの電圧(電位差)は
V1=(Vx-V)
V2=(Vx-0)
これと孤立部分に溜まる電荷の符号に気をつけて
電荷保存の式を作ると
あと=まえ
-C(Vx-V)+2C(Vx-0)=0
3CVx=CV (↓両辺×1/3)
Vx=1V/3
求まった電位Vxを
電圧(電位差)を示す式
V1=(Vx-V)
V2=(Vx-0)
に代入してC1、C2の電荷を求めると
Q1=-C(V/3-V)=-2V/3
Q2=C2V=2C*V/3=2V/3
ここでS1を開き、S2を閉じ
十分に時間がたったときの点Aの電位をV1とおく。
例の如くS1をきっている事で
C1に蓄えられた電荷は移動しないこと。
C2については、
はじめQ2=2CV/3の電荷がたくわえられ
あとの状態ではQ2v1=2CV1の電荷が溜まること。
C3については
はじめ電荷ゼロで
後の状態(十分時間がたってから)では
Q3v1=4CV1の電荷が溜まること。
C2とC3より下は
アースによって0Vになっているからそれぞれの電圧(電位差)は
V2=(V1-0)
V3=(V1-0)
となっている事などを考えて
C2とC3とで前後の電荷保存の式を立てると
まえ=あと
2CV/3=2CV1+4CV1
6CV1=2CV/3 (↓ 両辺×C/6)
V1=1V/9
が求まる。
<考察終わり>
自身の復習の効率を優先するばかりに
細かくなりすぎて、
だらしのない答案となってしまいましたので
怪しくヤバイ箇所も多数あると思います…。
ここまで読んで下さった方で
計算や表記ミス、もしくは
根本的な考え方の間違いに気付かれました方、
もっと要領のいい
漸化式の立て方などをご存知であられる方は
ご指摘を下さるとありがたいですm(_ _)m
でも、プギャー(^Д^)9mやら誹謗中傷は勘弁してくださいw …m(_ _)m
< TOPへ >





