受験数学って暗記！？(仮)～高校受験・大学受験～

と話題になったことがあったが，これは嘘である．



元々はTVで

「新しい指導要領では円周率は3として教える」

と言ったのが始まり．



それは指導要領のほんのごく一部分だけを見て言ったことである．


------------ 指導要領(一部加筆) --------------------------
3 内容の取扱い
(4)内容の「B 量と測定」の(1)のイ(円の面積の求め方を考え，それを用いること)
及び「C 図形」の(1)のエ(円周率の意味について理解すること)については，
円周率としては3.14を用いる が，
目的に応じて3を用いて処理できるよう配慮する ものとする．


指導要領は こちら へ．





これは2002年4月1日から施行されている指導要領であるが，
2003年東大理系第6問に次の問題が出題された．



円周率が3.05より大きいことを証明せよ．



高校生にこの問題を解かせてみると，
どうやるのかさっぱり分からないという返事ばかり．


「じゃあ円周率って何？」


と聞くと，決まって答えるのが・・・


「π！」

「3.141592・・・」


といったもの．






僕が聞きたいのはそうじゃないんだよね・・・ってことで


「円周率って元々どうやって定められたの？」


とさらに質問をする．




生徒 「う～ん・・・全然分からん」


僕 「小学校のときにやってるはずだけど覚えてない？」


生徒 「覚えてない」



僕が小学生のときには，直径が10cmの円盤を作って，滑らないように転がして円周を測って円周率を計算させられたんだけど，今はそういうのをやらないの？


こういう話をするとやったという生徒もいればやってないという生徒もいる．







大抵話が進まなくなるので，核心部分に一気に進む．


僕 「じゃあ円周の長さってどうやって求める？」


生徒 「直径×円周率」


僕 「そうだよね．ってことは円周率とは

『円周が直径に対して何倍であるか』

を表したものだよね．」





円周率がどのようにして考えられたかという点に着目すると，
この問題は「近似」を使うということが分かると思う．


つまり円周をある多角形の周の長さとして近似して計算すればいい．



仮に半径1の円に内接する正六角形で近似すると，その周の長さは6となる．

このとき，円の直径が2に対して周の長さが6であることから，円周率は3となる．



これでは証明できないので，もう少し円に近い多角形で近似することを考える．





半径1の円に内接する正n角形を考える．

各頂点と円の中心を結ぶと下図のような二等辺三角形がn個できる．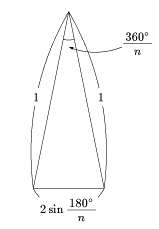





なるべく計算しやすい多角形を・・・と考えると，

正八角形はsin22.5°の計算で出てくる二重根号が面倒だし，正十角形はsin18°が面倒．

ということでsin15°なら簡単に求めることが出来るから，正十二角形でやってみようということになる．




正十二角形の周の長さは次のようになる．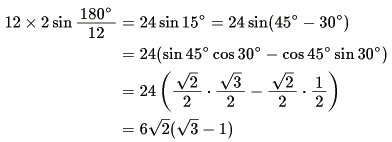






ここで，(円周の長さ)＞(正十二角形の周の長さ)であることを考えると





となる．さらに，





であることから近似値を計算すると次のようになり，円周率が3.05より大きいことが証明できる．






以上のように，その言葉(この場合では円周率)の意味を考えることによっても，ゴールへの道が開けることがある．