60ばーばの手習い帳

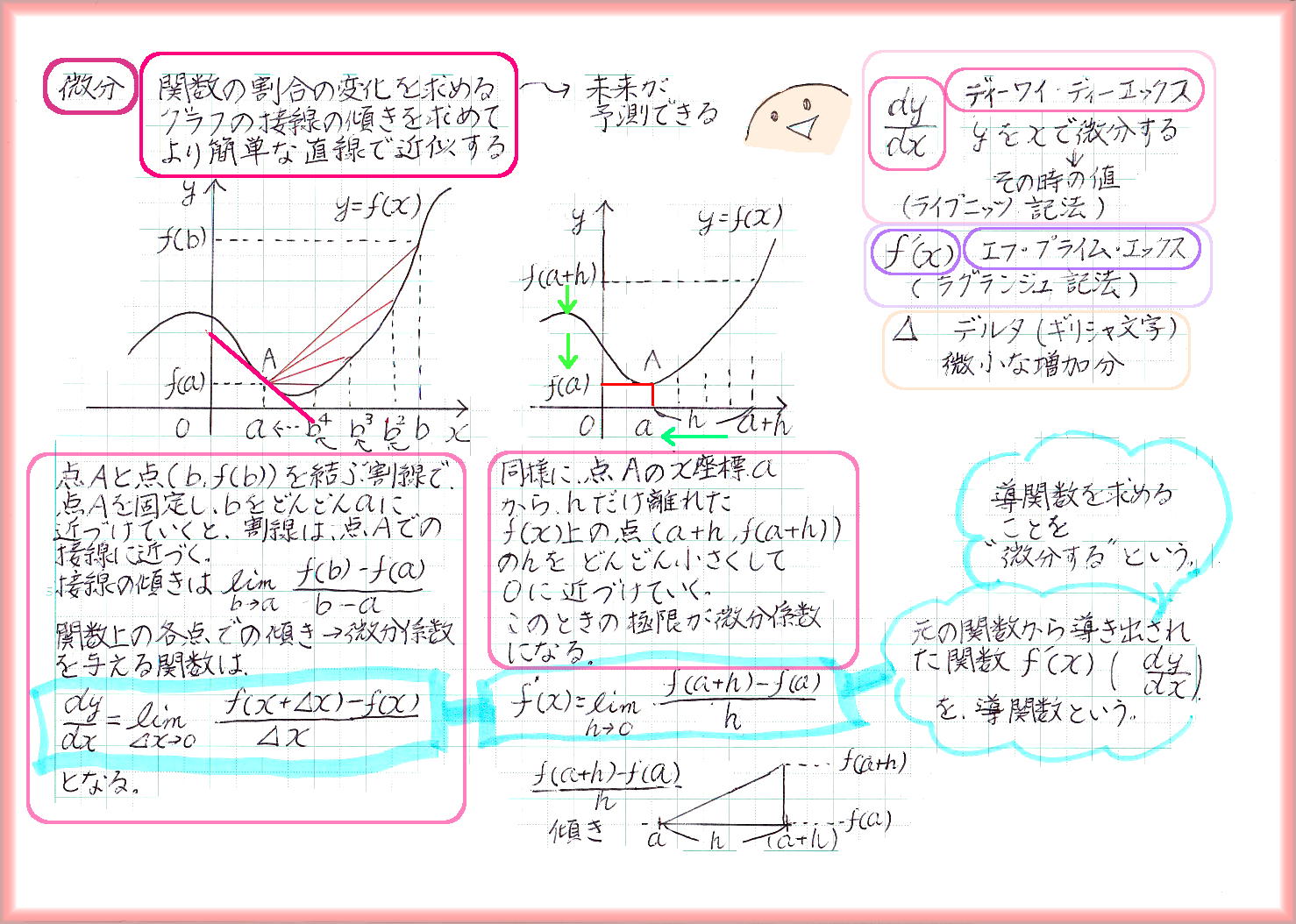
微分って見慣れない記号も出てきて難しいですね。上図が微分の概要なのですが、初心者には？？です。1つ1つ整理して頭の中に入れていく必要がありそうです。

　まずは極限、limという考えから。

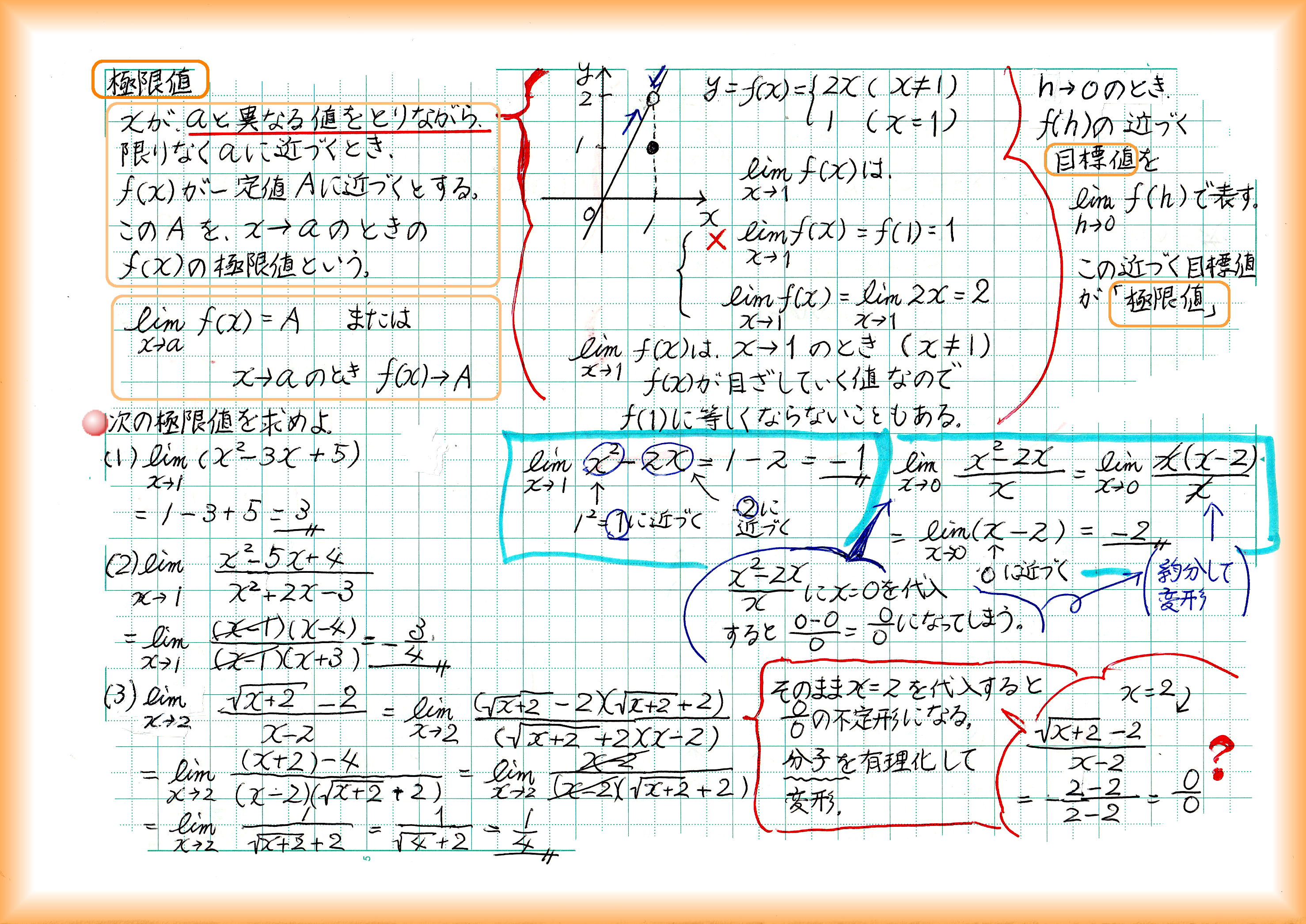
　「限界・境界」という意味で「タイムリミット」などと使われるlimit（リミット）は数学でも「限界・極限」の意味で使われます。
　「ａにはならないが、ａまでぎりぎり近づく、限りなくａに近づく」のがlimｘ→ａです。単純にｘにａを代入して計算できる場合もあれば、変形して計算する必要がある場合もあります。

　「平均変化率」の考え方は、小学校の算数から具体的な数で習ってきました。ａからｂまでの変化率は、2点を通る直線の傾きになります。

　2点間の距離をどんどん小さくしていくと、2点はほとんど1点で重なります。2点間の距離が「限りなく0に近づく」ときです。2点を通る直線は、その点での接線に近づくわけです。ある点での接線の傾きはその点での「微分係数」と呼ばれます。1つの関数の中でも、どの点を取るかで、微分係数は変化します。微分係数は具体的な値です。

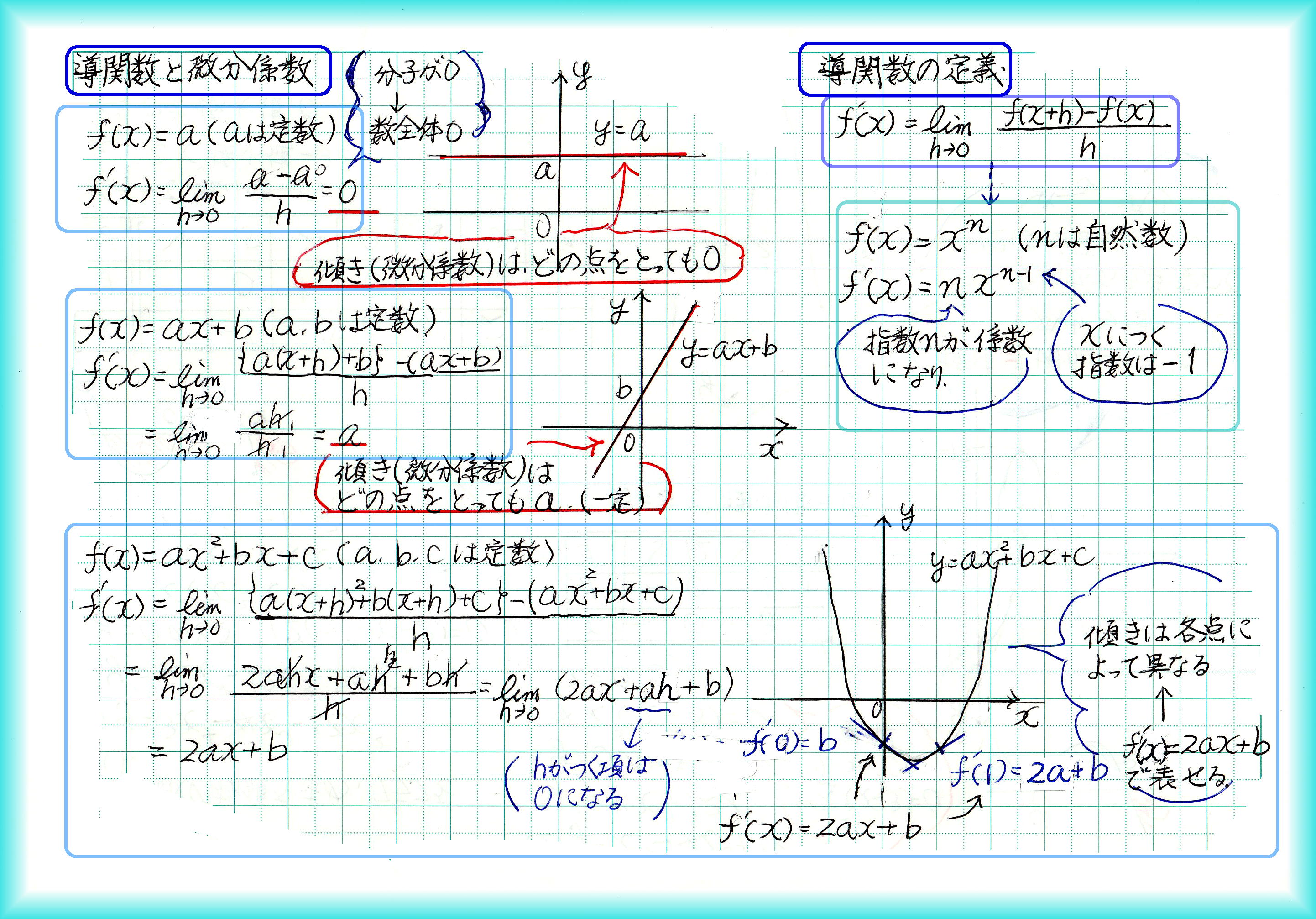
　具体的な数値である微分係数に対して、関数上のどんな点にもあてはまる接線の傾きを「関数」で表したのが「導関数」です。導関数は、具体的な値ではなく、Xを含む関数になります。ただ、f(ｘ)＝9のような定数関数は導関数が0になり、f(ｘ)＝9ｘの1次関数では導関数が9という定数になります。