2014年04月の記事
全23件 (23件中 1-23件目)
1
-

ブロー成形解析のための材料試験
共同研究をしている都内の大学に行ってきた。カナダの大学の試験機関で実施した樹脂の動的粘弾性試験、定常流試験、伸長粘土試験の再現実験を依頼していて、結果を見せてもらった。参照温度などのいくつかの違いはあったが、概ね再現できているようだった。この試験データを基にブロー成形解析ソフトの材料物性を入力して解析をし、カナダの試験結果を使ったときの解析結果と比較する予定。にほんブログ村
2014年04月30日
コメント(0)
-

仕事の構成要素
ふと、仕事の構成要素は以下の項目になると思った。1.顧客2.目的3.期限4.予算5.方法6.担当者7.価格=単価×数量つまり、顧客は誰で、何を欲しているのか?、いつまでなのか?、予算はいくらか?それに対して、どうやってやるか?、誰がやるか?、価格はいくらになるか?1~4が顧客側の要素、5~7が売り手側の要素。これらのどれが欠けても、仕事は成り立たない。したがって、これらを把握して仕事をしなくてはならないし、わからない場合は質問をして確認しなければならない。→自分への言い聞かせ。にほんブログ村
2014年04月29日
コメント(0)
-

物事へのとりかかり
何かを始めようとするとき、つい、ハードルを高く設定しすぎて始められなくなることがある。例えば仕事の場合、最初から顧客の要求を満たそうとして難しいことが多い。その場合、「とりあえず最低限ここまでならできる」(コミット)、という最低限のものを作り、これを修正して顧客の要求(ターゲット)に近づけることで進められることが多い。また、ぼくらの仕事の場合、顧客の要求が明確でないことも多く、その場合はこちらから提案する。こちらから提案する場合は、主導権がこちらにあるので、まずはこちらができること(コミット)を提案し、それを修正していくようにするとやりやすくなる。最初から「こうでなきゃダメ」とターゲットを狙うと難しいので、まずは、コミットで下限を抑えて、そこを出発点にしてターゲットを目指すと仕事が進めやすくなる。にほんブログ村
2014年04月28日
コメント(2)
-
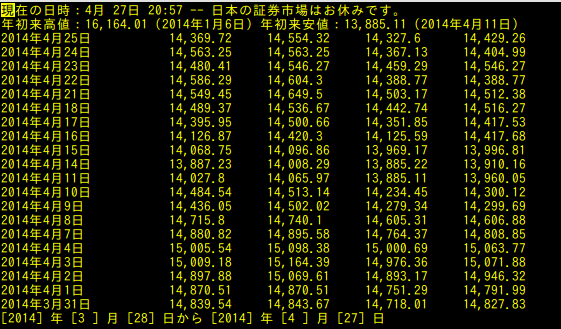
テキストブラウザw3m, lynx on lubuntu
前回の続き。w3mは表の形を保ったまま表示することができる。そこで、lubuntuの端末で、grepを使うと目的の情報に絞った状態をテキストにリダイレクトできる。w3m http://stocks.finance.yahoo.co.jp/stocks/history/?code=998407.O | grep "月" > aaa.txtとすると以下のように"月"と書かれている行だけがaaa.txtに抜き出される。にほんブログ村
2014年04月27日
コメント(0)
-

テキストブラウザw3m, lynx on lubuntu
通常、WEBブラウザといえば、Internet Explorer (以下IE)、FireFox, Chrome, Operaなどがメジャーなところだと思う。しかし、画像、動画はいっさい表示せず、テキストのみを表示するWEBブラウザがある。w3mとlynxだ。ほかにもあるようだけれど、有名なのはこの2つのようだ。なぜ、こんなブラウザに興味を持ったかというと、WEBスクレイピングに興味があるからだ。これまで、エクセルVBAでIEを自動操作して情報をエクセルに取り込むことをしていたけれど、IEを表示させると不要な画像や動画を含む広告のせいで遅くなる。そこで、画像、動画はいっさい表示しないテキストブラウザなら、もっと高速にWEBスクレイピングができると思った。それに、軽快なlubuntu環境でWEBスクレイピングをやってみたい。lubuntu環境で、これらのインストールはいたって簡単で、端末(LXTerminal)上でsudo apt-get install w3msudo apt-get install lynx-curと入力するだけでできてしまう。そして、例えば端末上でw3m http://w3m.sourceforge.net/index.ja.html > aaa.txtのように入力すると、w3mのホームページの内容をaaa.txtにリダイレクトすることができる。これがもっとも簡単なWEBスクレイピングかもしれない。にほんブログ村
2014年04月24日
コメント(0)
-

lubuntu14.04lts
古いデスクトップとノートパソコンでは13.10からのアップデートができなかったので、lubuntu14.04ltsをインストールし直した。↓ここから入手するのがわかりやすい。http://lubuntu-japan.jimdo.com/%E5%85%A5%E6%89%8B-%E5%B0%8E%E5%85%A5/今時のOSなのに、700MBのCD-Rに入ってしまう軽量さ。30分もかからずにインストールができてしまう。無事にインストールが終了した。軽快で使いやすい。にほんブログ村
2014年04月24日
コメント(0)
-

熱構造連成解析
アルミの構造物の表面温度が上昇した時の変形を解析している。以下の3つの方法がある。1.表面温度の上昇による熱膨張のみを考慮した線形静解析2.温度上昇を定常熱伝導解析で解き、定常状態となったときの温度分布で線形静解析3.温度上昇を非定常熱伝導解析で解き、最終状態の温度分布で線形静解析1.では温度分布は出力されないが、3.で時間を非常に短くしたときの結果と一致する。2.は3.で時間を非常に長くしたときの結果と一致する。要は、初期値として与えた表面温度の上昇が、構造物全体に行きわたらない状態が1.行きわたった状態が2.その過渡的な状態が3.となる。熱構造連成解析をするときは、時間の影響をどう取り扱うか考慮する必要がある。にほんブログ村
2014年04月23日
コメント(0)
-

lubuntu14.04にアップデート
新しいパソコンの仮想マシンVMware Playerに入っているlubuntuは何のトラブルもなく14.04にアップデートすることができた。古いマシンとは何が違うんだろう?大きな違いとしては、新しいマシンは64bitで古いマシンは32bitということがある。にほんブログ村
2014年04月21日
コメント(0)
-

lubuntuの不具合
古いパソコンでlubuntuを使っているのだけれど、2点不具合がある。1)音が出ない2)14.04にアップデートできない。1)については以下を参考にしてみたけれど、解決できていない。https://wiki.ubuntulinux.jp/UbuntuTips/Hardware/SoundTroubleshooting2)については以下のエラーが出て、アップデートができない。-----ここからW:gzip:/var/lib/apt/lists/partial/jp.archive.ubuntu.com_ubuntu_dists_trusty_universe_source_Sources の取得に失敗しました ハッシュサムが適合しません, W:gzip:/var/lib/apt/lists/partial/jp.archive.ubuntu.com_ubuntu_dists_trusty_universe_binary-i386_Packages の取得に失敗しました ハッシュサムが適合しません, E:いくつかのインデックスファイルのダウンロードに失敗しました。これらは無視されるか、古いものが代わりに使われます。-----ここまでなんでなんだろう?ぼちぼち調べてみよう。にほんブログ村
2014年04月21日
コメント(0)
-

total Lagrange法とupdated Lagrange法
非線形有限要素法では、時刻ゼロから時刻tまでの物体の状態は既知であり、時刻t'=t+Δtの状態を未知とする増分解析を想定する。時刻t'=t+Δtの状態を計算するために、時刻ゼロの状態を参照するのがtotal Lagrange法、時刻tの状態を参照するのがupdated Lagrange法である。total Lagrange法とupdated Lagrange法は本質的に違わない。算出される応力が現配置(UL)か初期配置(TL)かの違いであって、変形勾配テンソルFによって変換できる。大変形の弾塑性問題では、コーシー応力の客観速度で弾性変形を規定する亜弾性の構成モデルが採用される場合が多く、この場合の応力は応力速度の積分値として評価されるので、ULで直接内力を計算するほうがプログラム上は効率的。(いまさら聞けない計算力学の常識 第9話)【送料無料】いまさら聞けない計算力学の常識 [ 土木学会 ]Worked Examples in Nonlinear Continuum Mechanics for Finite Element Analysis-【電子書籍】【送料無料】非線形有限要素法の基礎と応用 [ 久田俊明 ]にほんブログ村
2014年04月17日
コメント(0)
-

温度応力解析
アルミ材料の構造物の特定の面に温度変化を与えた時の熱膨張による変形を解析している。出力は節点変位のみなので、ソルバーは線形性解析、荷重は温度荷重、材料特性に熱膨張率、参照温度、熱伝導率を入力し、熱膨張率×(荷重温度-参照温度)にしたがった変形を解析すればいい。温度分布も出力しようとすると、過渡熱伝導解析も設定する必要がある。過渡熱伝導解析は時間を導入し、時間ステップによる温度変化と最終ステップの温度による変形を線形性解析で計算する。変形が不要で、温度分布のみ必要であれば、定常熱伝導解析または過渡熱伝導解析を実施する。まわりの空気や接触部品との熱交換を考慮する場合には、熱伝達率と熱流束の設定が必要になる。最初、このあたりのことが整理しきれず、目的の解析をするまでにずいぶん悩んでしまった。解析ソフトによって設定方法が違うので、マニュアルをよく読む必要がある。にほんブログ村
2014年04月16日
コメント(0)
-

ブロー成形解析ソフトの押出し工程
開発元の押出し工程に関する論文から〇パリソン形状の定義直径スウェル、厚さスウェル、面積スウェル、パリソン長さ〇押出し工程でパリソン形状に影響する要素ダイ形状、ダイギャップ、流量、Weissenberg数、〇結果・ダイ出口の直径が小さいほうが直径スウェルが大きくなる。・ダイギャップが小さいほうが厚さスウェルが大きくなるが、直径スウェルは小さくなる。・流量は大きいほうが直径、厚さ、面積スウェルとも大きくなる。・Weissenberg数が大きいほうが直径、厚さ、面積スウェルとも大きくなる。↓参考文献http://onlinelibrary.wiley.com/doi/10.1002/pen.20662/abstractにほんブログ村
2014年04月15日
コメント(0)
-

ブログ開設2000日
いつもご訪問ありがとうございます。おかげさまでブログ開設2000日となりました。マイペースで、読んだ本、日々の出来事、考えたこと、株、CAEなど、思いつくままに書いてきました。「あれってなんだっけ?」というときに、自分のブログを検索して「そうだった」と確認できることもあります。これからもよろしくお願いします。にほんブログ村
2014年04月14日
コメント(1)
-

非線形有限要素法
〇応力の種類有限変形理論では、Cauchy応力テンソル、第1、第2Piora-Kirchhoff応力テンソルというのが出てくる。Cauchy応力は時刻tの現配置において定義され、真応力とも呼ばれる。第1Piora-Kirchhoff応力は、公称応力とも呼ばれ、基準配置の情報をもとに定義される。Cauchy応力をT、基準配置から現配置に至る体積変化をJ、変形勾配テンソルをF、第1Piora-Kirchhoff応力をΠとすると、T=(1/J)F・Πとなる。第1Piora-Kirchhoff応力は対称ではない。そこで、次のように対称な第2Piora-Kirchhoff応力Sを導入する。T=(1/J)F・S・FT非線形有限要素法で使う構成式と仮想仕事の原理式は第2Piora-Kirchhoff応力Sで記述される。にほんブログ村
2014年04月12日
コメント(0)
-

非線形有限要素法
2014年04月08日の続きGreen-LagrangeひずみテンソルE=(1/2)*(C-I)AlmansiひずみテンソルA=(1/2)*(I-Binv)BinvはBの逆テンソルE=FT・A・FC=U・RT・R・U=U^2Green-LagrangeひずみテンソルEは剛体回転の影響を受けない。AlmansiひずみテンソルAは剛体回転の影響を受ける。Fの左極分解式を使うとB=V・R・RT・V=V^2となる。変位uを用いてGreen-LagrangeひずみテンソルEとAlmansiひずみテンソルAを表すとE=(1/2)*(∂ui/∂Xj+∂uj/∂Xi+∂uk/∂Xi+∂uk/∂Xj)eiejeiejはディアディックA=(1/2)*(∂ui/∂Xj+∂uj/∂Xi-∂uk/∂Xi+∂uk/∂Xj)eiej微小変形、すなわち|∂ui/∂Xj|
2014年04月11日
コメント(0)
-

ブロー成形解析ソフトのベンチマーク解析報告
三重県の見込み客にブロー成形解析ソフトのベンチマーク解析報告をしてきました。ブロー成形で製造している自動車部品で、「肉折れ」という深いしわができる現象を再現できるかをベンチマーク解析として受けていました。やってみたところ、見事に再現していたので、いい報告ができました。ただ、すぐに導入というのは難しそうで、まずは受託解析として依頼したいようでした。PS.今日でWindows XP延長サポート終了。今日使ったパソコンはそのWindows XP。このパソコンを使うのも今日が最後になりそう。にほんブログ村
2014年04月09日
コメント(0)
-

非線形有限要素法
ブロー成形解析ソフトの計算モジュールには、非線形有限要素法が適用されている。カナダの開発元の論文と、非線形有限要素法に関する下の2冊の本を読んでいる。非線形有限要素法は有限変形理論を基礎としており、以下の項目を理解する必要がある。1.連続体力学の基礎テンソル、変形、ひずみ、ひずみ速度、応力、応力速度、構成式、境界値問題と仮想仕事の原理2.幾何学的非線形有限要素解析の枠組み仮想仕事式の増分分解と離散化最初のテンソルの演算を理解するのがしんどい。総和規約は面倒だけど、一度、すべての成分を書き下して眺めないとわからない。テンソルは0階がスカラー、1階がベクトル、2階がマトリクスまではわかるけど、3階は成分が箱型に立体的に並んでおり、4階はもはや、幾何学的な成分の並びとしては理解できない。どうにかテンソルとその演算を理解すると、さっそく変形を記述するための変形勾配テンソルFが出てくる。変形勾配テンソルFは基準配置Xの増分dXと現配置xの増分dxを関係付ける。dx=F・dXこの変形勾配テンソルFはRを直交テンソル、Uを正値対称テンソルとしたとき、F=R・Uの形に分解される。これを右極分解という。なぜこんな右極分解をするかというと、以下の右Cauchy-Green変形テンソルCを定義すると、C=FT・FFTはFの転置UがCの固有ベクトル方向に固有値倍の伸縮を表し、Rが伸縮なしの剛体回転を表すからである。右Cauchy-Green変形テンソルCはK-BKZモデルにも出てくる。同様にFの左極分解も定義される。F=V・RB=F・FTただし、B=R・C・RTふう、しんどい。今日はここまでにしとこう。Worked Examples in Nonlinear Continuum Mechanics for Finite Element Analysis-【電子書籍】【送料無料】非線形有限要素法の基礎と応用 [ 久田俊明 ]にほんブログ村
2014年04月08日
コメント(0)
-

マンション管理組合の書類
管理組合の理事長印を受け取ったので、主に名義変更書類に記入しました。明日、管理会社に返送します。現代社会では、とにかく物事に書類がついてまわるので、読み書きの作業を強いられますよね。面倒くさいですが、慣れるしかありません。マンション管理組合関連の議事録などの書類がどんどんたまっていくので、スキャンをして処分をしました。うちではscansnapを重宝しています。スマホやタブレットへのWi-Fi接続スキャンを実現したScanSnap ix500シリーズ。【ポイント5倍(4/...価格:37,800円(税込、送料込)にほんブログ村
2014年04月06日
コメント(0)
-
リトルアジアのカレー
目黒川の桜を見た後、グルーポンで購入したクーポンを使い、赤坂のリトルアジアというカレー屋で夕食を食べました。ナンが香ばしくてとてもおいしかったです。http://www.groupon.jp/cid/116476?recom=NO↓サラダとパパド(インドのおせんべいのような揚げもの)↓サフランライスとナンと豆カレーにほんブログ村
2014年04月05日
コメント(1)
-

目黒川の桜
目黒川の桜を見に行きました。約800本のソメイヨシノが植えられているそうです。今日は結構寒かったのですが、たくさんの見物人が川岸を歩いていました。にほんブログ村
2014年04月05日
コメント(0)
-

職場の花見
毎年恒例の職場の花見。サポートがなかなか終わらず、少し遅れて会社を出て、上野公園の会場に向かった。上野公園での開催場所を地図で探して1時間くらい上野公園をさまよってしまった。やっとの思いで開催場所にたどり着くと、そこには誰もいなかった。会社に電話したら、あいにくの雨なので途中で撤収して会社のデモルームに会場を移したということだった。。。ぼくはちょうど行き違いになってしまったようだ。会社に戻り、50分遅れで花見に参加した。やれやれ。↓不忍の池の桜にほんブログ村
2014年04月04日
コメント(0)
-

ブロー成形解析ソフトの定式化
カナダが開発元のブロー成形解析ソフトの定式化についてだいぶわかってきた。このソフトが扱うブロー成形は押出しブローと延伸ブローの2種類である。そのうち、押出しブローの文献を見つけて読んでみた。↓押出しブローの画像https://www.google.co.jp/search?q=%E6%8A%BC%E5%87%BA%E3%81%97%E3%83%96%E3%83%AD%E3%83%BC&rlz=1C1CHMO_jaJP564JP564&espv=210&es_sm=93&source=lnms&tbm=isch&sa=X&ei=Img9U8fNE8aVkgX2jYD4DQ&ved=0CAkQ_AUoAg&biw=1366&bih=643押出しブローは大体、以下の工程となっている。押出し→型締め→ブロー→冷却押出し工程では、ダイ内の樹脂流動とダイから吐出されるパリソンとが分けて定式化されている。ダイ内樹脂流動では樹脂をニュートン流体と仮定してCarreauモデル、WLFモデルを使用して定式化している。ダイから吐出されるパリソンは固形物として扱われ、有限変形理論で定式化している。樹脂にはCarreauモデル、WLFモデル、KBKZモデルが適用されている。型締め→ブロー工程では、ダイから吐出されるパリソン同様に固形物として扱われ、有限変形理論で定式化している。樹脂にはKBKZモデルが適用されている。計算には、パリソンを三角形平面応力要素で離散化した有限要素法が適用されている。温度変化は過渡熱伝導解析FEMで計算される。有限変形理論では応力に2ndパイオラキルヒホッフ応力、ひずみにGreen-Laglangeひずみが使われている。仮想仕事の原理から、力=剛性×変位の形のマトリクス方程式に帰着する。KBKZモデルでは、応力がコーシー応力となっている。2ndパイオラキルヒホッフ応力とコーシー応力が変形勾配テンソルで関係付けられている。↓参考文献http://papers.sae.org/2013-01-1397/http://nparc.cisti-icist.nrc-cnrc.gc.ca/npsi/ctrl?action=shwart&index=an&req=16891233⟨=enにほんブログ村
2014年04月03日
コメント(1)
-
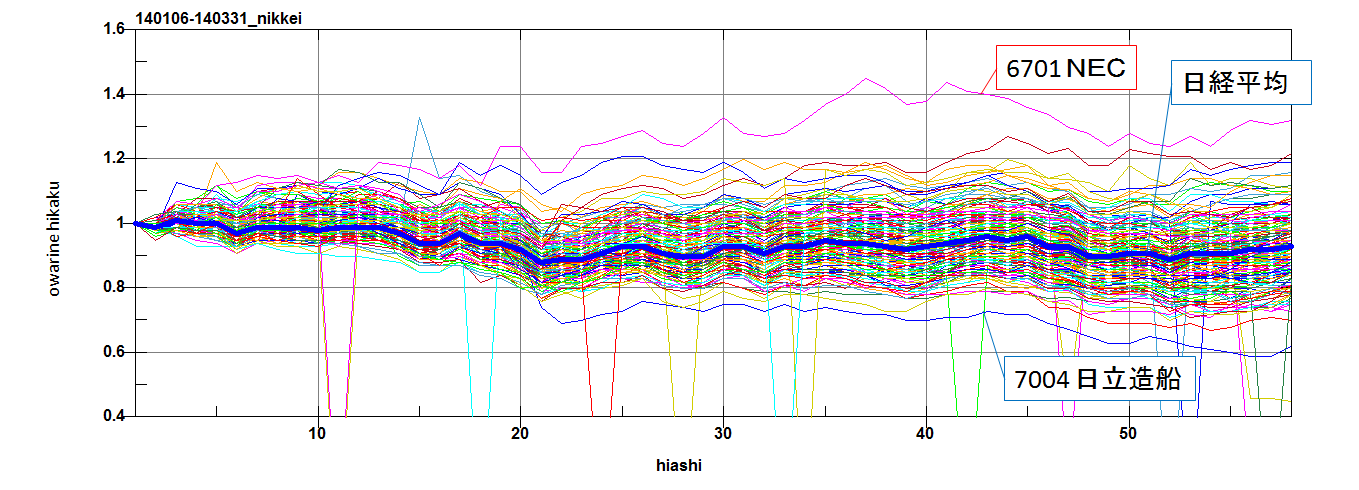
日経平均構成銘柄の3か月比較チャート
日経平均構成銘柄222銘柄の1/6から3/31までの比較チャートを作成してみた。1/6の終値が1となるように規格化している。真ん中の太い青線が日経平均225である。一番上がっていたのが、6701NEC、途中で下がっていたのが7004日立造船だった。ところどころ、急に下がっているところは、データが抜けたり、株式分割しているところである。1/6から3/31で、日経平均は0.93倍、1倍より大きいのは39銘柄、小さいのは179銘柄、ちょうど1倍だったのが3銘柄だった。にほんブログ村
2014年04月01日
コメント(0)
全23件 (23件中 1-23件目)
1
-
-

- お勧めの本
- ★「ひとりぼっちになることが大事」…
- (2025-11-29 08:14:12)
-
-
-

- ボーイズラブって好きですか?
- ヒロアカのBL同人誌!緑谷出久と爆豪…
- (2025-07-10 07:00:04)
-
-
-

- 読書
- キャベツ炒めに捧ぐ / 井上 荒野
- (2025-11-30 00:00:13)
-







