くぴんのブログ

プロフィール

くぴん７４

フォローする

フリーページ

家電

(1)

バックナンバー

2025年11月
2025年10月
2025年09月

2025年08月
2025年07月

お気に入りブログ

5.　バリュー投資対… New! みきまるファンドさん

DOW 47716.42 +289.3… New! どらりん0206さん

楽天ラッキーくじ更…

New! じゃっかすさん

まさかの Maryu21さん

自分を愛することは… まりあのじいじさん

ニューストピックス

キーワードサーチ

▼キーワード検索

< 新しい記事

新着記事一覧(全5115件)

過去の記事 >

2021年09月08日

高次要素の精度確認 #FEM, #有限要素法

テーマ： 3D-CAD＆CAE使いこなしてますか？？(183)

カテゴリ： CAE

メッシュ作成なしで、CADデータに直接、境界条件を設定して解析できるソフトを仕事で使っている。
その計算方法を勉強するために、高次の有限要素について調べてみた。計算中にメッシュを更新するアダプティブメッシュ法には、h法とp法がある。h法は要素を細分化して計算精度を高めるのに対し、p法は要素の形状関数の次数を上げて計算精度を高める。どちらも節点数が増えるために自由度数が増え、計算コストが上がる。アダプティブメッシュ法は必要なところに対して、メッシュを細分化したり、形状関数の次数を上げる。高次の要素は大きな領域を少ない要素で精度よく解析できる。
以下のスライドの片持ちはりの例題で四角形要素1要素で精度確認をしてみた。

↓いまさら聞けない計算力学の常識　講習会スライド
http://www.jsce.or.jp/committee/amc/compmech/pdftext121204/kurumatani.pdf

以下の自作エクセルVBAを使った。

結果は以下。

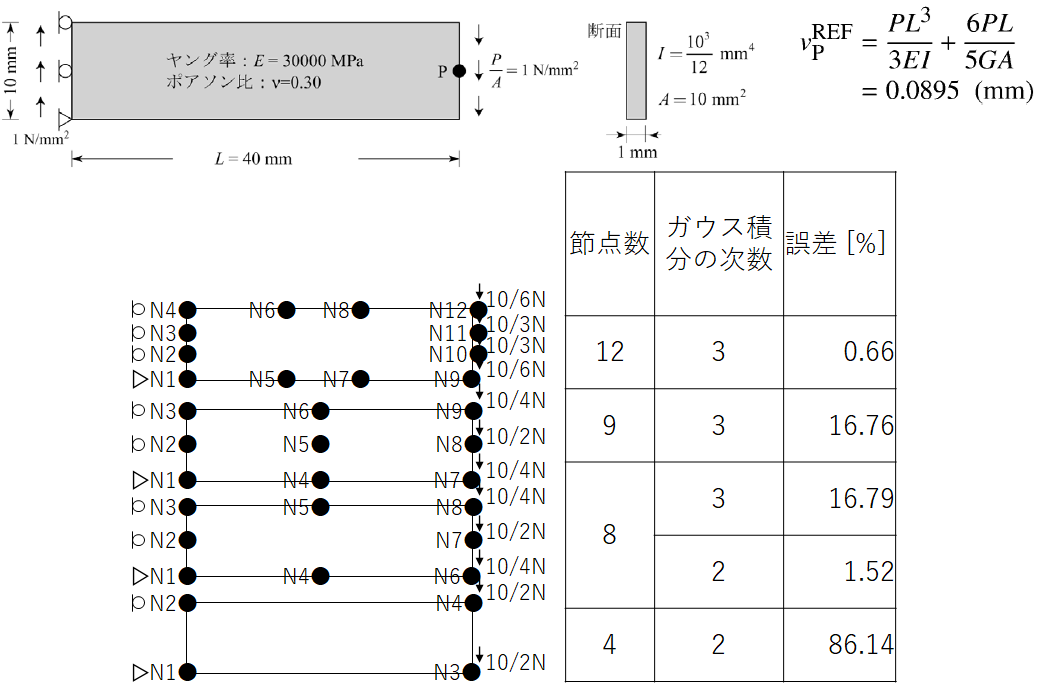
せん断曲げの領域内の変位は３次式であり、12節点要素は形状関数が4次のため、正確に変位を求めることができる。9節点要素と8節点要素はガウス積分の次数が３次のときはほぼ同等だった。4節点は予想通り精度が悪かった。面白いのは、8節点要素でガウス積分の次数を２次とした方が３次とするよりも精度がいいことだった。また、9節点と12節点ではガウス積分の次数を２次とすると解が出ず、３次にする必要があった(気づいて修正するのに２日かかった)。形状関数の次数に適したガウス積分の次数を使う必要があるようだ。
この問題に対しては、計算コストと精度のバランスが最もいいのは８節点であるが、9節点、12節点の要素は今回初めて作って勉強になった。
1軸引張りでは領域内の変位場が1次関数のため、三角形要素でも、ゆがんだ要素でも形状関数が1次のため精度よく解が出るが、純曲げは領域内の変位場が2次、せん断曲げは３次のため、形状関数の次数も2次、3次が必要になる。