PR
X
フリーページ
おすすめCD

DREAM THEATER

EXTREME

DEF LEPPARD

MR.BIG

METALLICA

MEGADETH

LOSTPROPHETS

HOOBASTANK

TRAPT

FOO FIGHTERS

EAGLES

System Of A Down
ローンの計算方法
橘玲
クレジットカードのしくみ
大切な言葉集
この世界を混乱に導く悪魔のルール
ETF140銘柄チャート画像取得マクロ
エクセルVBAで高速フーリエ変換
株・資産運用

1.株式会社の始まり

2.資産形成の方程式

3.利回りに対する理解

4.単利と複利

5.債券価格

6.キャピタルゲインとインカムゲイン

7.株式投資の投資戦略

8.BS(貸借対照表)とPL(損益計算書)の関係

9.リスクと不確実性について

10.72の法則

11.家賃から物件価格を推定する方法

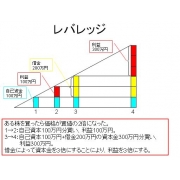
12.レバレッジ

13.ファンダメンタル指標

14.サラリーマンの生涯賃金

15.BPS+EPS×10の有効性

16. 裁定取引 (arbitrage)
fortran90で高速フーリエ変換
カレンダー
DOW 44296.51 +426.1…
New!
どらりん0206さん
2021~24PF概況493位… New! みきまるファンドさん
楽天ラッキーくじ更… じゃっかすさん
じゃっかすさん
訃報相次ぐ Maryu21さん
自分を愛することは… まりあのじいじさん
2021~24PF概況493位… New! みきまるファンドさん
楽天ラッキーくじ更…
 じゃっかすさん
じゃっかすさん訃報相次ぐ Maryu21さん
自分を愛することは… まりあのじいじさん
キーワードサーチ
▼キーワード検索
カテゴリ: プログラミング
・23人以上の人が集まれば、同じ誕生日の人が一組以上いる確率は1/2を超える。57人以上いれば、確率は99%になる。
ちょっと直感的には理解できない。
計算してみる。
誕生日の数はうるう年の2/29も入れると366。
2人の誕生日が異なる確率は順列をPとすると366P2/366^2。
23人がすべて異なる誕生日である確率は、366P23/366^23。
同じ誕生日の人が一組以上いる確率はこの確率を1から引く。
pythonで計算すると以下のようになる。
In [30]: import math
Out[31]: 0.49367698818054007
In [32]: 1-math.perm(366,23)/366**23
Out[32]: 0.5063230118194599
57人の場合は以下。
In [33]: 1-math.perm(366,57)/366**57
Out[33]: 0.9899897980651987
2人から57人のときの確率を描画してみる。
In [34]: x=range(2,58)
In [39]: y=[1-math.perm(366,i)/366**i for i in range(2,58)]
In [36]: import matplotlib.pyplot as plt
In [40]: plt.plot(x,y)
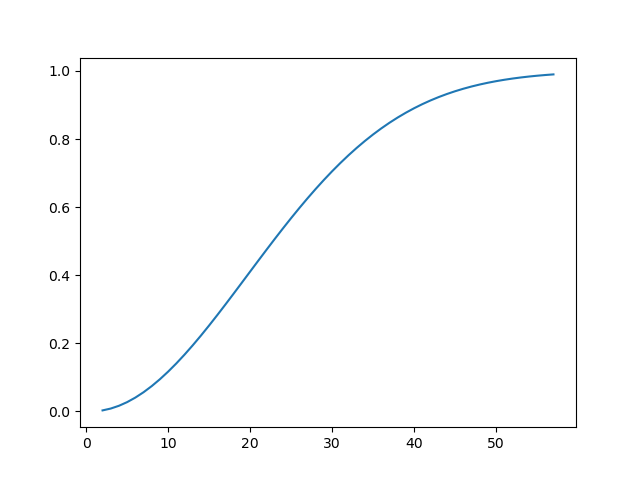
こんなカーブを描かれると確かに間違える。

にほんブログ村
ちょっと直感的には理解できない。
計算してみる。
誕生日の数はうるう年の2/29も入れると366。
2人の誕生日が異なる確率は順列をPとすると366P2/366^2。
23人がすべて異なる誕生日である確率は、366P23/366^23。
同じ誕生日の人が一組以上いる確率はこの確率を1から引く。
pythonで計算すると以下のようになる。
In [30]: import math
Out[31]: 0.49367698818054007
In [32]: 1-math.perm(366,23)/366**23
Out[32]: 0.5063230118194599
57人の場合は以下。
In [33]: 1-math.perm(366,57)/366**57
Out[33]: 0.9899897980651987
2人から57人のときの確率を描画してみる。
In [34]: x=range(2,58)
In [39]: y=[1-math.perm(366,i)/366**i for i in range(2,58)]
In [36]: import matplotlib.pyplot as plt
In [40]: plt.plot(x,y)

こんなカーブを描かれると確かに間違える。
にほんブログ村
お気に入りの記事を「いいね!」で応援しよう
[プログラミング] カテゴリの最新記事
-
Pyxel Python向けレトロゲームエンジン 2024年01月08日
-
pythonでテトリス 2024年01月07日
-
人口動態シミュレーション python 2023年07月17日
【毎日開催】
15記事にいいね!で1ポイント
10秒滞在
いいね!
--
/
--
© Rakuten Group, Inc.