[CAE] カテゴリの記事
全296件 (296件中 1-50件目)
-

Sfepy Version 2024.2 released
6/28にVersion 2024.2がリリースされた。毎年4回リリースされる。↓リリースノートhttps://sfepy.org/doc-devel/release_notes.html#id12024年6月28日 バージョン 2024.2 リリース (マルチポイント制約条件と新しい例題、混合フレキソエレクティシティの項、改良された新しい固有値ソルバーなど)。詳細はリリースノートを参照28.06.2024 Version 2024.2 released (multi-point constraints terms + new example, mixed formulation flexoelecticity terms, improved and new eigenvalue problem solvers, etc.), see release notes.↓インストール方法https://sfepy.org/doc-devel/installation.html以下のコマンドでインストールできた。pip install sfepy 以下のコマンドではまだ2024.1だった。conda install -c conda-forge sfepy↓テスト結果$ sfepy-test略======================= 216 passed in 427.11s (0:07:07) ========================$ pipでインストールしたせいか、warningが出なくなった。にほんブログ村
2024年06月30日
コメント(0)
-

Sfepy Version 2024.1 released
3/29にVersion 2024.1がリリースされた。毎年4回リリースされる。↓リリースノートhttps://sfepy.org/doc-devel/release_notes.html#id12024.03.29 バージョン 2024.1 リリース (新しい領域内定数フィールド近似、新しい項: 指数関数的弾性応答を備えたパッシブ大変形ファイバー、改善されたソルバー ステータス レポート、ウェッジ要素と例題、マルチノード線形結合 (境界) 条件と例題など)、詳細はリリースノートを参照29.03.2024 Version 2024.1 released (new constant-in-a-region field approximation, new term: passive large deformation fibres with exponential elastic response, improved solver status reporting, wedge elements + example, multi-node linear combination (boundary) conditions + example, etc.), see release notes.↓インストール方法https://sfepy.org/doc-devel/installation.htmlソースからビルドしようとするとエラーが出てうまくいかなくなり、以下のコマンドでインストールした。conda install -c conda-forge sfepy↓テスト結果$ sfepy-test-- Docs: https://docs.pytest.org/en/stable/how-to/capture-warnings.html================ 209 passed, 2520 warnings in 426.90s (0:07:06) ================$ にほんブログ村
2024年03月30日
コメント(0)
-
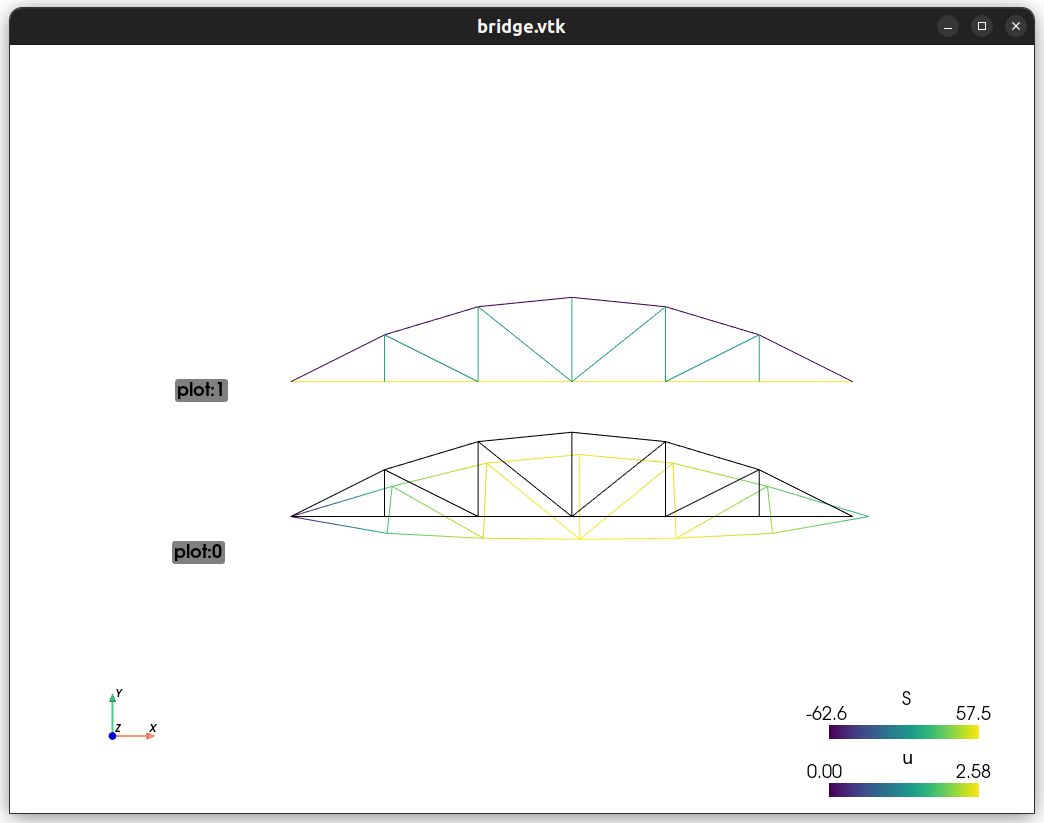
Sfepy Version 2023.4 released
12/29にVersion 2023.4がリリースされた。毎年4回リリースされる。↓リリースノートhttps://sfepy.org/doc-devel/release_notes.html#id12023.12.29 バージョン 2023.4 リリース (新しい構造要素 (線形ばね、線形トラス)、スペクトル要素法 (LGL 求積法およびラグランジュ基底のノード)、異なる要素を持つメッシュの初期サポート、新しい例題: 2D および 3D トラス橋 、h リファインメント固有値収束、ヘキサ要素とテトラ要素で構成されるビーム、ギャラリーに含まれるさらに多くの例など)、詳細はリリース ノートを参照。29.12.2023 Version 2023.4 released (new structural elements (linear spring, linear truss), spectral element method (LGL quadrature and nodes with Lagrange basis), initial support for meshes with elements of different topological dimensions, new examples: 2D and 3D truss bridge, h-refinement eigenvalue convergence, beam consisting of hexa and tetra elements, many more examples included in gallery, etc.), see release notes.↓インストール方法https://sfepy.org/doc-devel/installation.htmlソースからビルドしようとするとエラーが出てうまくいかなくなり、以下のコマンドでインストールした。conda install -c conda-forge sfepy↓テスト結果$ sfepy-test-- Docs: https://docs.pytest.org/en/stable/how-to/capture-warnings.html================ 209 passed, 2519 warnings in 421.70s (0:07:01) ================2Dトラスの例題https://sfepy.org/doc-devel/examples/linear_elasticity-truss_bridge.html3Dトラス、構造要素とソリッド要素の混合モデルhttps://sfepy.org/doc-devel/examples/linear_elasticity-truss_bridge3d.htmlh リファインメント固有値収束https://sfepy.org/doc-devel/examples/miscellaneous-refine_evp.htmlprimmeのインストールがエラーになり、再現できなかった。ヘキサ要素とテトラ要素で構成されるビームこの例題は見つからなかった。今回は、例題がいつもより増えていた。にほんブログ村
2023年12月30日
コメント(0)
-

Sfepy Version 2023.3 released
9/29にVersion 2023.3がリリースされた。毎年4回リリースされる。↓リリースノートhttps://sfepy.org/doc-devel/release_notes.html#id12023.09.29 バージョン 2023.3 リリース (非線形拡散および体積力項を示す例題、新しい感度項、POC, JAX ベースの自動微分可能項 (弾性、質量) + 弾性力学パラメーター識別の例題など)29.09.2023 Version 2023.3 released (example demonstrating nonlinear diffusion and volume forces terms, new sensitivity term, proof-of-concept JAX-based auto-differentiable terms (elasticity, mass) + elastodynamics parameter identification example, etc.), see release notes.↓インストール方法https://sfepy.org/doc-devel/installation.html↓テスト結果$ sfepy-testsfepy/tests/test_units.py .. [ 99%]sfepy/tests/test_volume.py .. [100%]==================================== warnings summary ====================================略====================== 213 passed, 17 warnings in 457.45s (0:07:37) ======================$ にほんブログ村
2023年09月30日
コメント(0)
-

Sfepy Version 2023.2 released
6/29にVersion 2023.2がリリースされた。毎年4回リリースされる。↓リリースノートhttps://sfepy.org/doc-devel/release_notes.html#id12023.06.29 バージョン 2023.2 リリース (numpy.distutils を scikit-build (cmake) に置き換え、PRIMME 固有値問題ソルバーのインターフェイス、新しいモーダル解析の例題、新しい用語: 非線形拡散および非線形体積力など)29.06.2023 Version 2023.2 released (replace numpy.distutils by scikit-build (cmake), interface for the PRIMME eigenvalue problem solver, new declarative modal analysis example, new terms: nonlinear diffusion and nonlinear volume forces, etc.), see release notes.↓インストール方法https://sfepy.org/doc-devel/installation.html↓テスト結果$ sfepy-test --output-dir=output-testssfepy/tests/test_units.py .. [ 99%]sfepy/tests/test_volume.py .. [100%]==================================== warnings summary ====================================sfepy/tests/test_declarative_examples.py::test_examples[homogenization/linear_elastic_mM.py]/home/user/anaconda3/lib/python3.10/site-packages/scikits/umfpack/umfpack.py:736: UmfpackWarning: (almost) singular matrix! (estimated cond. number: 2.59e+12)warnings.warn(msg, UmfpackWarning)sfepy/tests/test_declarative_examples.py::test_examples[linear_elasticity/linear_elastic_up.py]/home/user/anaconda3/lib/python3.10/site-packages/scikits/umfpack/umfpack.py:736: UmfpackWarning: (almost) singular matrix! (estimated cond. number: 3.43e+12)warnings.warn(msg, UmfpackWarning)-- Docs: https://docs.pytest.org/en/stable/how-to/capture-warnings.html====================== 211 passed, 2 warnings in 423.80s (0:07:03) =======================$ ↓新しい固有値解析の例題を確認してみた。PRIMME eigenvalue problem solverを使っている。pip intall primmeでインストールする必要がある。https://sfepy.org/doc-devel/examples/linear_elasticity-modal_analysis_declarative.html↓モード3のモードシェイプAnsysの結果とほぼ同様ということだ。mailing listでもこれについて議論されていた。https://mail.python.org/archives/list/sfepy@python.org/thread/6LX7G6UPWUCBPPYYS2OUAQ72H5ER6CQU/にほんブログ村
2023年07月02日
コメント(0)
-

sfepy 非定常熱伝導解析の例題
以下の例題を確認してみた。https://sfepy.org/doc-devel/examples/diffusion-time_heat_equation_multi_material.html↓計算ログsfepy: ====== time 6.000000e+01 (step 120 of 120) =====sfepy: updating variables...sfepy: ...donesfepy: updating materials...sfepy: heat_losssfepy: heat_flux_defined_by_funcsfepy: platesfepy: cylindersfepy: powdersfepy: ...done in 0.00 ssfepy: nls: iter: 0, residual: 1.287746e+00 (rel: 1.000000e+00)sfepy: residual: 0.01 [s]sfepy: matrix: 0.00 [s]sfepy: solve: 0.00 [s]sfepy: nls: iter: 1, residual: 2.529867e-12 (rel: 1.964571e-12)Warning: Ignoring XDG_SESSION_TYPE=wayland on Gnome. Use QT_QPA_PLATFORM=wayland to run on Wayland anyway.sfepy: solved in 120 steps in 6.27 seconds$ ↓Monicaによる解説-----このコードは、熱方程式を解くための `sfepy` ライブラリを使用したサンプルスクリプトです。このスクリプトは、レーザーパウダーベッド融合加工プロセスに着想を得ています。このプロセスでは、レーザーソースが定期的な時間間隔で円形の表面にフラックスを沈積させます。熱はビルドプレートに伝播し、シリンダーの側面にある粉末に伝わります。熱損失は、熱が沈積される表面と底板の両方でニュートン型の熱交換を介して発生します。このスクリプトでは、熱方程式の弱い形式を解いて、離散化されたフィールド `T` を求めます。このフィールドは、一様な初期条件から始まり、時間とともに変化します。最後の時間ステップの結果フィールドは、isosurface として可視化できます。また、温度の時間変化は出力ディレクトリに画像ファイルとして保存されます。コードの中で使用される定数や変数には以下が含まれます:- `nominal_heat_flux`: 表面に沈積される平均熱フラックス- `alpha`: 粉末の熱伝導率- `t_start`: 熱源が加熱を開始する時間- `t_stop`: 熱源が加熱を停止する時間- `T0`: 初期温度- `h`: ニュートン型熱交換係数- `mm`: ミリメートル単位の長さを表す定数- `filename_mesh`: メッシュファイルのパスまた、このスクリプトは、SI 単位系(メートル、キログラム、ジュールなど)を使用しますが、温度は摂氏で表されます。-----にほんブログ村
2023年04月30日
コメント(0)
-
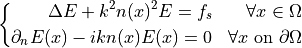
sfepy WiFiの伝搬の可視化
アパートの部屋で2.4GHzのWiFiがどのように伝搬するかを可視化する2Dの例題。MonicaというChat GPTのchrome拡張機能に解説してもらった。https://chrome.google.com/webstore/detail/monica-%E2%80%94-your-chatgpt-cop/ofpnmcalabcbjgholdjcjblkibolbppbファイル名がacousticsとか書いてるけれど、電波の伝搬の例題。https://sfepy.org/doc-devel/examples/acoustics-helmholtz_apartment.html↓ヘルモホルツの支配方程式↓アパートの部屋の区画 2Dメッシュ↓ポテンシャルEの虚部のコンター左下のソースから右上に離れるに従い、壁と減衰で弱くなっている。にほんブログ村
2023年04月29日
コメント(0)
-

Sfepy Version 2023.1 released
3/29にVersion 2023.1がリリースされた。毎年4回リリースされる。↓リリースノートhttps://sfepy.org/doc-devel/release_notes.html#id1異なるトポロジーを持つメッシュのサポート、体積積分と表面積分の統一した処理、弾性力学ソルバーの更新、相互質量行列アルゴリズム、地震荷重とピエゾ弾性力学の例題、CI に GitHub Actions を使用するなど)。 29.03.2023 Version 2023.1 released (support meshes with cells of different topological dimensions, unified treatment of volume and surface integrals, updated elastodynamics solvers, reciprocal mass matrix algorithm, seismic load and piezo-elastodynamics examples, use GitHub Actions for CI, etc.), see release notes.↓インストール方法https://sfepy.org/doc-devel/installation.html↓テスト結果$ sfepy-test --output-dir=output-tests================================== test session starts ===================================platform linux -- Python 3.8.5, pytest-7.1.2, pluggy-1.0.0......-- Docs: https://docs.pytest.org/en/stable/how-to/capture-warnings.html==================== 211 passed, 14287 warnings in 540.30s (0:09:00) =====================$↓新しいピエゾ弾性力学の例題を確認してみたhttps://sfepy.org/doc-devel/examples/multi_physics-piezo_elastodynamic.html↓ポテンシャルpのコンターと変形(5000倍に拡大)にほんブログ村
2023年03月30日
コメント(0)
-

Sfepy Version 2022.4 released
12/29にVersion 2022.4がリリースされた。毎年4回リリースされる。↓リリースノートhttps://sfepy.org/doc-devel/release_notes.html#id1複数材料の非定常電熱解析とスカラーヘルムホルツ方程式の例題、弾性動解析ソルバーのアダプティブタイムステップ、中央差分ソルバーなど29.12.2022 Version 2022.4 released (new examples: transient heat equation with several material domains and scalar Helmholtz equation, adaptive time step control for elastodynamics solvers, central difference elastodynamics solver, etc.), see release notes.↓インストール方法https://sfepy.org/doc-devel/installation.html↓テスト結果$ python -c "import sfepy; sfepy.test()"-- Docs: https://docs.pytest.org/en/stable/how-to/capture-warnings.html===================== 206 passed, 1429 warnings in 418.81s (0:06:58) =====================$にほんブログ村
2022年12月29日
コメント(0)
-
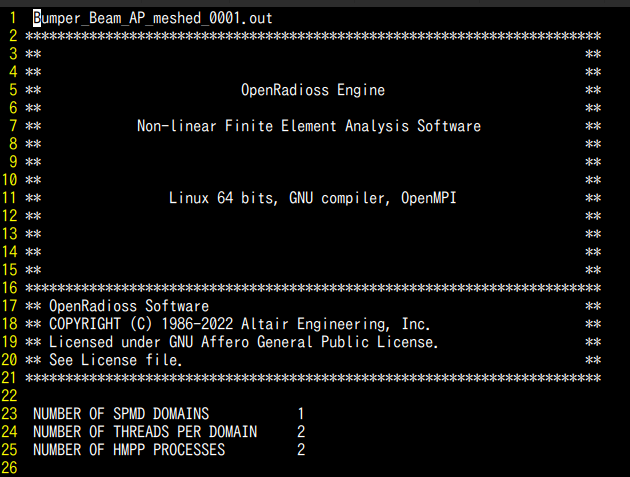
OpenRadioss
リリース(9/8)から間が空いたが、Ubuntu 22.04.1 LTSにダウンロード&ビルドしてバンパーのモデルを計算してみた。↓例題モデル集https://www.openradioss.org/models/↓outファイルメモリ8GB, Core i5の2CPUではこの小さいモデルでも20分くらいかかった。結果表示はh3dをHyperViewPlayerに読み込んだ。アニメーションは表示できるが、コンター表示ができない。。ポスト処理に課題がある。これまでの構造系オープンソースソフトに比べると飛躍的に解析の幅が広がる。大きな利点は以下と考える。・多くのパートからなるアセンブリモデルを接触を考慮して衝突計算できる・豊富な材料モデル (弾塑性材、ゴムなどの超弾性体、フォーム材など)・SPHでバードストライクや流体を扱えるetc.にほんブログ村
2022年10月10日
コメント(0)
-

Sfepy Version 2022.3 released
9/29にVersion 2022.2がリリースされた。毎年4回リリースされる。↓リリースノートhttps://sfepy.org/doc-devel/release_notes.html#id1ついにpip installでインストールできるようになった。linear esastodynamicsが速くなったようだ。均質化法ベースのマイクロスケール解析の改善29.09.2022 Version 2022.3 released (reorganized scripts, PyPI support, speed-up of linear elastodynamics problems, improved homogenization-based recovery of micro-scale solutions, etc.), see release notes.↓インストール方法https://sfepy.org/doc-devel/installation.html↓テスト結果$ python -c "import sfepy; sfepy.test()"================================== test session starts ===================================platform linux -- Python 3.8.5, pytest-7.1.2, pluggy-1.0.0rootdir: /home/...plugins: anyio-3.5.0collected 203 items ...===================== 203 passed, 1720 warnings in 392.24s (0:06:32) =====================$ 前(744.30s)よりだいぶ速くなった。Ubuntu2022.4LTSのせいかもしれないけど。にほんブログ村
2022年09月29日
コメント(0)
-

実験 モーダル解析の概要 一連の手順 構造と振動
モーダル振動試験の実施手順がよくわかる動画なのでメモ。https://www.youtube.com/watch?v=rWJnW75vCkkモード法の周波数応答解析は、固有値解析をやって固有周波数、固有モードベクトルを求めてから周波数応答解析の順になるが、実験では逆。試験体にモード形状がわかるように配置(非常に重要)された加速度センサから周波数応答関数を取得し、その周波数応答関数の位相差からモードベクトル(モード形状)を求める。固有値解析では減衰をゼロとして固有周波数、固有モードベクトルを求めるが、実験では減衰も伝達関数から求められる。にほんブログ村
2022年08月06日
コメント(0)
-
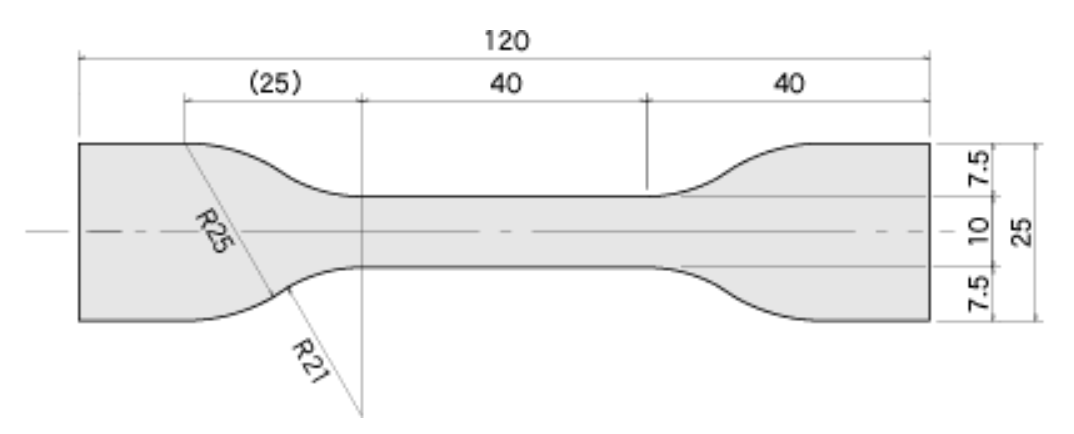
sfepy Mooney-Rivlinモデルを使ったゴムのダンベル1号引張試験シミュレーション
以下の例題を参考に標記のシミュレーションをやってみた。https://sfepy.org/doc-devel/examples/large_deformation-hyperelastic_tl_up_interactive.htmlダンベル1号は以下の寸法、厚さは2mm↓XX応力コンターアニメーション↓FEMシミュレーションとMooney-Rivlinの理論式との比較節点数2277、要素数1360sfepy: reading mesh (./dumbbell1gou.bdf)...sfepy: number of vertices: 2277sfepy: number of cells:sfepy: 3_8: 1360sfepy: ...done in 0.06 s計算時間はJupyter lab上で52秒で思ったより速い。オープンソースCAEソフトでこれをやっている例はあまり見たことがない。sfepyは超弾性モデル(neohook, mooney-rivlin, yeoh)や連成解析の例題が充実している。にほんブログ村
2022年07月31日
コメント(0)
-
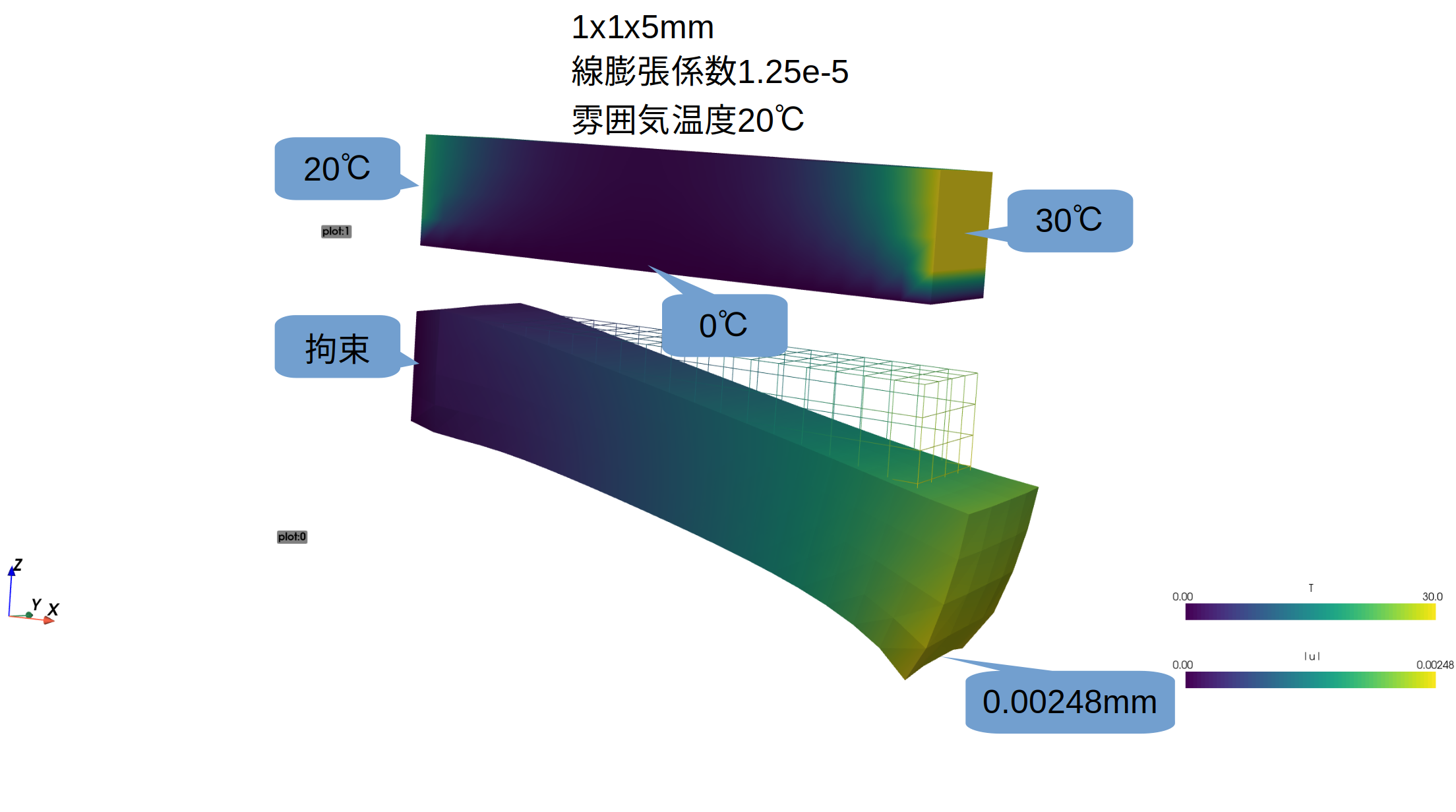
sfepy 熱構造連成解析の例題
以下の熱構造連成解析の例題を確認してみた。https://sfepy.org/doc-devel/examples/multi_physics-thermo_elasticity_ess.html左側20℃、右側30℃、下側0℃、雰囲気温度20℃という条件で定常熱伝導解析をし、出てくる温度分布が上側の図。この温度分布と線膨張係数で変形する。左側を拘束し、下側が温度が低いので縮むため、下側の図のように変形する。にほんブログ村
2022年07月18日
コメント(0)
-

Sfepy Version 2022.2 released
6/29にVersion 2022.2がリリースされた。毎年4回リリースされる。↓リリースノートhttps://sfepy.org/doc-devel/release_notes.html#id1・pytestにかわるカスタムテストコード、pyvistaベースの改善された可視化スクリプトなどVersion 2022.2 released (custom testing code replaced by pytest, improved pyvista-based visualization script, etc.)↓インストール方法https://sfepy.org/doc-devel/installation.html↓テスト結果$python -m pytest sfepy/tests================================== test session starts ==================================platform linux -- Python 3.8.5, pytest-6.2.5, py-1.10.0, pluggy-1.0.0rootdir: /home/pyontaku14/sfepy-master/sfepyplugins: anyio-2.2.0collected 203 items sfepy/tests/test_assembling.py .... [ 1%]sfepy/tests/test_base.py ...... [ 4%]sfepy/tests/test_cmesh.py .. [ 5%]sfepy/tests/test_conditions.py .... [ 7%]sfepy/tests/test_declarative_examples.py ........................................ [ 27%]................... [ 36%]sfepy/tests/test_dg_field.py ........... [ 42%]sfepy/tests/test_dg_terms_calls.py .......... [ 47%]sfepy/tests/test_domain.py ....... [ 50%]sfepy/tests/test_eigenvalue_solvers.py . [ 51%]sfepy/tests/test_elasticity_small_strain.py .. [ 52%]sfepy/tests/test_fem.py .. [ 53%]sfepy/tests/test_functions.py ... [ 54%]sfepy/tests/test_high_level.py .... [ 56%]sfepy/tests/test_homogenization_engine.py .. [ 57%]sfepy/tests/test_homogenization_perfusion.py . [ 58%]sfepy/tests/test_hyperelastic_tlul.py . [ 58%]sfepy/tests/test_io.py .. [ 59%]sfepy/tests/test_laplace_unit_disk.py . [ 60%]sfepy/tests/test_laplace_unit_square.py .. [ 61%]sfepy/tests/test_lcbcs.py .... [ 63%]sfepy/tests/test_linalg.py .... [ 65%]sfepy/tests/test_linear_solvers.py .. [ 66%]sfepy/tests/test_linearization.py . [ 66%]sfepy/tests/test_log.py . [ 66%]sfepy/tests/test_matcoefs.py .... [ 68%]sfepy/tests/test_mesh_expand.py . [ 69%]sfepy/tests/test_mesh_generators.py ...... [ 72%]sfepy/tests/test_mesh_interp.py ...... [ 75%]sfepy/tests/test_mesh_smoothing.py . [ 75%]sfepy/tests/test_meshio.py ..... [ 78%]sfepy/tests/test_msm_laplace.py . [ 78%]sfepy/tests/test_msm_symbolic.py .. [ 79%]sfepy/tests/test_normals.py . [ 80%]sfepy/tests/test_parsing.py .. [ 81%]sfepy/tests/test_poly_spaces.py .... [ 83%]sfepy/tests/test_projections.py .... [ 85%]sfepy/tests/test_quadratures.py .. [ 86%]sfepy/tests/test_ref_coors.py .. [ 87%]sfepy/tests/test_refine_hanging.py .. [ 88%]sfepy/tests/test_regions.py .. [ 89%]sfepy/tests/test_semismooth_newton.py . [ 89%]sfepy/tests/test_sparse.py . [ 90%]sfepy/tests/test_splinebox.py .... [ 92%]sfepy/tests/test_tensors.py .... [ 94%]sfepy/tests/test_term_call_modes.py . [ 94%]sfepy/tests/test_term_consistency.py ...... [ 97%]sfepy/tests/test_term_sensitivity.py . [ 98%]sfepy/tests/test_units.py .. [ 99%]sfepy/tests/test_volume.py .. [100%]=================================== warnings summary ====================================l===================== 203 passed, 637 warnings in 744.30s (0:12:24) =====================$リリースノートのようにテストが変わっていた。にほんブログ村
2022年06月30日
コメント(0)
-

Sfepy Version 2022.1 released
3/30にVersion 2022.1がリリースされた。毎年4回リリースされる。↓リリースノートhttps://sfepy.org/doc-devel/release_notes.html#id1・状態変数の新しい処理方法と状態クラスの削除、多くの新しい複数の線形項に基づく感度解析など。(30.03.2022 Version 2022.1 released (new handling of state variables data and State class removal, many new sensitivity analysis terms based on multi-linear term implementation, etc.), see release notes.)↓インストール方法https://sfepy.org/doc-devel/installation.html↓テスト結果[109] tests/test_term_sensitivity.py+++ test_sensitivity: ok[110] tests/test_units.py+++ test_consistent_sets: ok+++ test_units: ok[111] tests/test_volume.py+++ test_volume: ok+++ test_volume_tl: ok111 test file(s) executed in 378.63 s, 0 failure(s) of 206 test(s)$にほんブログ村
2022年03月30日
コメント(0)
-

Sfepy Version 2021.4 released
12/29にVersion 2021.4がリリースされた。毎年、年間4回リリースされる。↓リリースノートhttps://sfepy.org/doc-devel/release_notes.html#id1・改善されたpyvistaベースの可視化、galleryをreview.pyで作成、均質化ツール、新しいドライウォーターの例題など。(29.12.2021 Version 2021.4 released (improved pyvista-based visualization script resview.py, gallery images generated using resview.py, homogenization tools: new parallel recovery of multiple microstructures, new “dry water” flow example, etc.), see release notes.)↓インストール方法https://sfepy.org/doc-devel/installation.html↓テスト結果[109] tests/test_term_sensitivity.py+++ test_sensitivity: ok[110] tests/test_units.py+++ test_consistent_sets: ok+++ test_units: ok[111] tests/test_volume.py+++ test_volume: ok+++ test_volume_tl: ok111 test file(s) executed in 368.49 s, 0 failure(s) of 206 test(s)$にほんブログ村
2021年12月29日
コメント(0)
-

Sfepy Version 2021.3 released
9/29にVersion 2021.3がリリースされた。↓リリースノートhttps://sfepy.org/doc-devel/release_notes.html#id1・統一された体積とサーフェスの積分項、改善されたpyvistaベースの可視化など。(unified volume and surface integration terms, improved pyvista-based visualization script, etc.)↓インストール方法https://sfepy.org/doc-devel/installation.html↓テスト結果+++ test_vector_matrix: ok[109] tests/test_term_sensitivity.py+++ test_sensitivity: ok[110] tests/test_units.py+++ test_consistent_sets: ok+++ test_units: ok[111] tests/test_volume.py+++ test_volume: ok+++ test_volume_tl: ok111 test file(s) executed in 359.99 s, 0 failure(s) of 206 test(s)$最近、メーリングリストへの投稿が増えてきている。少しずつ注目されているのかもしれない。にほんブログ村
2021年09月29日
コメント(0)
-

高次要素の精度確認 #FEM, #有限要素法
メッシュ作成なしで、CADデータに直接、境界条件を設定して解析できるソフトを仕事で使っている。その計算方法を勉強するために、高次の有限要素について調べてみた。計算中にメッシュを更新するアダプティブメッシュ法には、h法とp法がある。h法は要素を細分化して計算精度を高めるのに対し、p法は要素の形状関数の次数を上げて計算精度を高める。どちらも節点数が増えるために自由度数が増え、計算コストが上がる。アダプティブメッシュ法は必要なところに対して、メッシュを細分化したり、形状関数の次数を上げる。高次の要素は大きな領域を少ない要素で精度よく解析できる。以下のスライドの片持ちはりの例題で四角形要素1要素で精度確認をしてみた。↓いまさら聞けない 計算力学の常識 講習会スライドhttp://www.jsce.or.jp/committee/amc/compmech/pdftext121204/kurumatani.pdf以下の自作エクセルVBAを使った。結果は以下。せん断曲げの領域内の変位は3次式であり、12節点要素は形状関数が4次のため、正確に変位を求めることができる。9節点要素と8節点要素はガウス積分の次数が3次のときはほぼ同等だった。4節点は予想通り精度が悪かった。面白いのは、8節点要素でガウス積分の次数を2次とした方が3次とするよりも精度がいいことだった。また、9節点と12節点ではガウス積分の次数を2次とすると解が出ず、3次にする必要があった(気づいて修正するのに2日かかった)。形状関数の次数に適したガウス積分の次数を使う必要があるようだ。この問題に対しては、計算コストと精度のバランスが最もいいのは8節点であるが、9節点、12節点の要素は今回初めて作って勉強になった。1軸引張りでは領域内の変位場が1次関数のため、三角形要素でも、ゆがんだ要素でも形状関数が1次のため精度よく解が出るが、純曲げは領域内の変位場が2次、せん断曲げは3次のため、形状関数の次数も2次、3次が必要になる。9節点、12節点要素の経常関数は以下の本のP111, 112を参照した。↓参考書籍↓参考リンクhttps://moridesignoffice.com/FEM-sum-4.htmlにほんブログ村
2021年09月08日
コメント(0)
-

Sfepy Version 2021.2 released
6/29にVersion 2021.1がリリースされた。↓リリースノートhttps://sfepy.org/doc-devel/release_notes.html#id1・新しい感度分析項、バーンスタイン多項式に基づく正のFE基底、一定の材料パラメータを持つ項のより小さなメモリ使用など。(new sensitivity analysis terms, positive FE basis based on Bernstein polynomials, smaller memory footprint of terms with constant material parameters, etc.)↓インストール方法https://sfepy.org/doc-devel/installation.html最近、メーリングリストへの投稿が増えてきている。少しずつ注目されているのかもしれない。にほんブログ村
2021年06月29日
コメント(0)
-

sfepyをWindows 10に導入
Linux(Ubuntu) PCを失ってしまったので、Windows 10にsfepyを導入してみた。最初に以下のようにしてAnacondaでmeshioなどもインストールする必要がある。conda install sfepyhttps://github.com/sfepy/sfepyビルドするためにCコンパイラを以下からダウンロード&インストール。https://sourceforge.net/projects/mingw-w64/files/Toolchains%20targetting%20Win32/Personal%20Builds/mingw-builds/installer/mingw-w64-install.exe/downloadまた、Microsoft Visual studioもダウンロード&インストール。https://visualstudio.microsoft.com/ja/downloads/MinGWのRun terminal上でsfepy-masterフォルダにcdコマンドで移動し、以下のコマンドでC exetnsionをビルドするとできた。python setup.py build_ext --inplacehttp://sfepy.org/doc-devel/installation.html#compilation-of-c-extension-modulesインストール。pip setup.py installテストpython run_tests.py[110] tests\test_volume.py+++ test_volume: ok+++ test_volume_tl: ok110 test file(s) executed in 1042.34 s, 0 failure(s) of 205 test(s)無事、すべてのテストをパスした。にほんブログ村
2021年03月31日
コメント(0)
-

Sfepy Version 2021.1 released
3/30にVersion 2021.1がリリースされた。↓リリースノートhttp://sfepy.org/doc-devel/release_notes.html#id1・非正方の係数行列、複数の線形解析項、ディリクレ境界、周期境界の改善、例題にリンクする項の表など (non-square homogenized coefficient matrices, new implementation of multi-linear terms, improved handling of Dirichlet and periodic boundary conditions in common nodes, terms in the term table document linked to examples, etc.)↓インストール方法http://sfepy.org/doc-devel/installation.htmlWindows 10のAnacondaでインストールしようとしているが、ビルドがうまくいかず苦戦中。やっぱりUbuntuじゃないとだめなのか。にほんブログ村
2021年03月30日
コメント(0)
-

Sfepy Version 2020.4 released
12/27にVersion 2020.4がリリースされた。↓リリースノートhttp://sfepy.org/doc-devel/release_notes.html#id1・Ogden超弾性モデル、セレンディピティ1-3次有限要素など。27.12.2020 Version 2020.4 released (Ogden hyperelastic term, serendipity finite element basis of orders 1-3, etc.), see release notes.↓インストール方法http://sfepy.org/doc-devel/installation.html0. 必要なライブラリの準備 (K)Ubuntusudo apt-get install python-scipy python-matplotlib python-tables python-pyparsing libsuitesparse-dev python-setuptools mayavi2 python-dev ipython python-sympy cython python-sparseUbuntuで、ソースからビルドするのが一番確実。1. sfepyを置きたいディレクトリでgithubからコピー。通常ホームディレクトリgit clone git://github.com/sfepy/sfepy.git2. cdでsfepyフォルダに入ってCエクステンションをコンパイル。inplaceが無難。python setup.py build_ext --inplace3. インストールpython setup.py install4. テストpython ./run_tests.py↓テスト結果[111] tests/test_volume.py+++ test_volume: ok+++ test_volume_tl: ok
2020年12月27日
コメント(0)
-

Sfepy Version 2020.3 released
9/29にVersion 2020.3がリリースされた。↓リリースノートhttp://sfepy.org/doc-devel/release_notes.html#id1・pyvistaによる新しい可視化、Yeoh超弾性モデルと例題など。new script for visualizations based on pyvista, generalized Yeoh hyperelastic term + example, etc.↓インストール方法http://sfepy.org/doc-devel/installation.html0. 必要なライブラリの準備 (K)Ubuntusudo apt-get install python-scipy python-matplotlib python-tables python-pyparsing libsuitesparse-dev python-setuptools mayavi2 python-dev ipython python-sympy cython python-sparseUbuntuで、ソースからビルドするのが一番確実。1. sfepyを置きたいディレクトリでgithubからコピー。通常ホームディレクトリgit clone git://github.com/sfepy/sfepy.git2. cdでsfepyフォルダに入ってCエクステンションをコンパイル。inplaceが無難。python setup.py build_ext --inplace3. インストールpython setup.py install4. テストpython ./run_tests.py↓テスト結果[111] tests/test_volume.py+++ test_volume: ok+++ test_volume_tl: ok
2020年09月29日
コメント(0)
-

sfepy HEXA1要素 1軸引張・圧縮解析
以下の例題を改変して線形弾性体、Neohook、Mooney-Rivlinについて引張・圧縮解析をやってみた。http://sfepy.org/doc-devel/examples/large_deformation-compare_elastic_materials.html1辺1mmの立方体HEXA1要素で、Z方向に荷重を与え、Z変位を取得する。↓荷重-変位グラフ↓引張アニメーション(Mooney Rivlin)↓圧縮アニメーション(Mooney Rivlin)以下、備忘録的にポイントをメモ(インデントが壊れる)メッシュの定義def mesh_hook(mesh, mode): """ Generate the block mesh. """ mesh = gen_block_mesh([1.0, 1.0, 1.0], [2, 2, 2], [0.5, 0.5, 0.5], name='el3', verbose=False) #size, number of nodes, center position return mesh filename_mesh = UserMeshIO(mesh_hook)材料の定義materials = { 'solid' : ({ 'K' : 8.333, # bulk modulus 'mu_nh' : 3.846, # shear modulus of neoHookean term 'mu_mr' : 1.923, # shear modulus of Mooney-Rivlin term 'kappa' : 1.923, # second modulus of Mooney-Rivlin term # elasticity for LE term 'D' : stiffness_from_lame(dim=3, lam=5.769, mu=3.846), },), 'load' : 'empty', }境界条件の定義ebcs = { 'Fix' : ('origin', {'u.all' : 0.0}), 'xyz100' : ('xyz100', {'u.[1,2]' : 0.0}), 'xyz010' : ('xyz010', {'u.[0,2]' : 0.0}), 'xyz001' : ('xyz001', {'u.[0,1]' : 0.0}), 'xyz110' : ('xyz110', {'u.[2]' : 0.0}),}解くべき支配方程式equations = { 'linear' : """dw_lin_elastic.i.Omega(solid.D, v, u) = dw_surface_ltr.isurf.Top(load.val, v)""", 'neo-Hookean' : """dw_tl_he_neohook.i.Omega(solid.mu_nh, v, u) + dw_tl_bulk_penalty.i.Omega(solid.K, v, u) = dw_surface_ltr.isurf.Top(load.val, v)""", 'Mooney-Rivlin' : """dw_tl_he_neohook.i.Omega(solid.mu_mr, v, u) + dw_tl_he_mooney_rivlin.i.Omega(solid.kappa, v, u) + dw_tl_bulk_penalty.i.Omega(solid.K, v, u) = dw_surface_ltr.isurf.Top(load.val, v)""", }にほんブログ村
2020年09月06日
コメント(0)
-

sfepy 鉄板と剛体球との接触シミュレーション
sfepy2020.2を使ってタイトルの解析をやってみた。以下の例題を改変した。http://sfepy.org/doc-devel/examples/linear_elasticity-elastic_contact_sphere.html鉄板は100x100x8mm,ヤング率210000MPa,ポアソン比0.3,メッシュサイズ2mm、周囲を完全拘束剛体球は幾何学的に中心を(50,50,20)、半径30mmとして鉄板中央に配置し、初期貫入がZ方向に18mmあるように配置する。この初期貫入を解消するように鉄板が変形をしていく。剛体球の形状は表示されないが、見やすくするために、メッシュをつくって配置した。↓Y=0断面のミーゼス応力球のメッシュはFreeCADを使うと簡単に作成できた。これで、鉄の塑性を考慮できるようにすれば、塑性加工シミュレーションっぽいことができるかも。でもsfepyだと塑性を考慮させるコードをユーザが書かないとならないので結構大変そう。実行時間は151秒だった。sfepy: nls: iter: 11, residual: 1.024128e+05 (rel: 1.145848e-03)sfepy: residual: 0.05 [s]sfepy: matrix: 0.47 [s]sfepy: solve: 10.08 [s]sfepy: nls: iter: 12, residual: 2.254950e+04 (rel: 2.522956e-04)sfepy: residual: 0.05 [s]sfepy: matrix: 0.47 [s]sfepy: solve: 10.12 [s]sfepy: nls: iter: 13, residual: 1.047277e+03 (rel: 1.171748e-05)sfepy: residual: 0.05 [s]sfepy: matrix: 0.48 [s]sfepy: solve: 10.10 [s]sfepy: nls: iter: 14, residual: 6.902052e-04 (rel: 7.722377e-12)sfepy: updating variables...sfepy: ...donesfepy: setting up dof connectivities...sfepy: ...done in 0.00 ssfepy: matrix shape: (39015, 39015)sfepy: assembling matrix graph...sfepy: ...done in 0.29 ssfepy: matrix structural nonzeros: 2667717 (1.75e-03% fill)sfepy: updating variables...sfepy: ...donesfepy: setting up dof connectivities...sfepy: ...done in 0.00 ssfepy: matrix shape: (36015, 36015)sfepy: assembling matrix graph...sfepy: ...done in 0.27 ssfepy: matrix structural nonzeros: 2459925 (1.90e-03% fill)sfepy: solved in 1 steps in 151.86 seconds$にほんブログ村
2020年08月29日
コメント(0)
-

XSim Elmerの使い方メモ
2次元の流体構造連成解析と3次元の構造の非線形過渡応答解析の例題をのせている。https://www.xsim.info/articles/Elmer/How-to-use-Elmer.html↓2次元の流体構造連成解析の結果↓3次元の構造の非線形過渡応答解析の結果Windows版のGUIでやってみたけれど、使いやすい。Elmerは連成解析が得意ということだ。方程式をしっかり指定するところが、フリーソフトっぽいけれど、ユーザーは何の微分方程式を解こうとしているか認識できる。例題のメッシュは境界条件を設定するエッジやフェースがグループ分けされた状態だったけれど、本来はここも指定しなくてはならないところで、面倒くさいところ。本腰を入れてやれば、いろいろな解析ができそうだ。でも、なかなか難しいんだけれど。にほんブログ村
2020年08月26日
コメント(0)
-
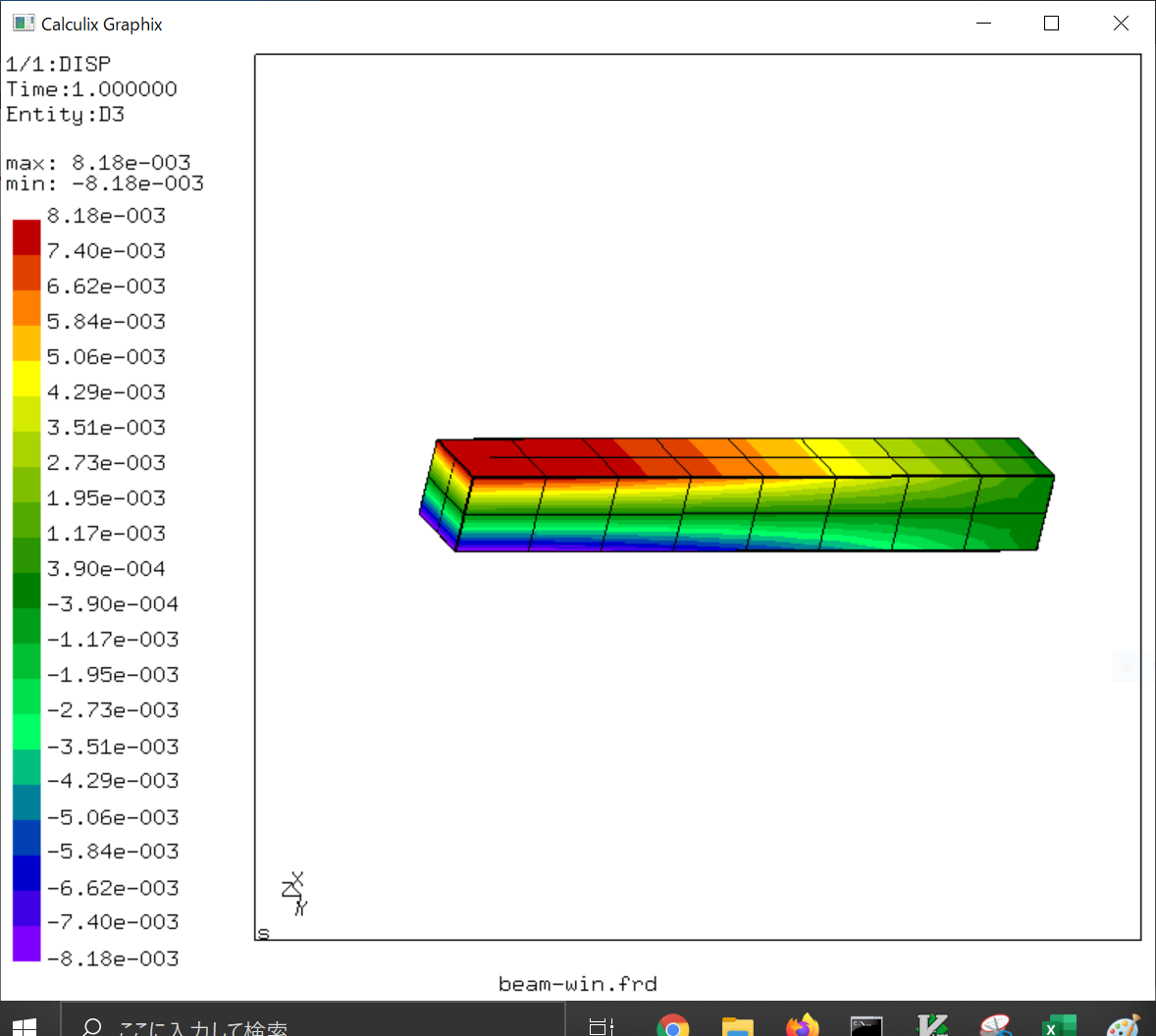
CAE、物理シミュレーション - XSim
OpenFOAM® 用の解析設定データを作成できるウェブサービスを提供している以下のページの技術ドキュメントがすごい!https://www.xsim.info/FreeCAD, OpenFOAM, CalculiX, MeshLab, Elmer, OpenModelicaといったOpen CAEソフトのチュートリアルが公開されている。Open CAEソフトのリストもある。https://www.xsim.info/articles/Notes/OSS-CAE-softwares-list.html試しにCalculiXの片持ち梁の例題をやってみた。Wiondows版はbatファイルを実行し、CalculiXを実行できるコマンドプロンプトで計算実行をする。この技術ドキュメントのチュートリアルはできる限りフォローしたいところだ。にほんブログ村
2020年08月25日
コメント(0)
-

Equation of Motion(運動方程式)とMomentum Equation(運動量方程式)
結局同じ。ニュートンの運動の第2法則を表す式はEquation of Motion(運動方程式)とよばれる。ma=Fm:質量、a:加速度、F:力Momentum Equation(運動量方程式)は運動量保存の法則を記述する。d(mv)/dt=Fv:速度質量が変化しなければ、m(dv/dt)=Fa=dv/dtからma=F厳密ではないけれど。にほんブログ村
2020年08月24日
コメント(0)
-

Sfepy Version 2020.2 released
6/30にVersion 2020.2がリリースされた。sfepyのロゴが変わっていた。↓リリースノートhttp://sfepy.org/doc-devel/release_notes.html#id1・不連続ガラーキン法の実装とサンプル、新しいウェブサイトデザイン、メモリー使用の改善など。discontinuous Galerkin method implementation and examples, new website look, memory usage improvements, etc.↓インストール方法http://sfepy.org/doc-devel/installation.html0. 必要なライブラリの準備 (K)Ubuntusudo apt-get install python-scipy python-matplotlib python-tables python-pyparsing libsuitesparse-dev python-setuptools mayavi2 python-dev ipython python-sympy cython python-sparseUbuntuで、ソースからビルドするのが一番確実。1. sfepyを置きたいディレクトリでgithubからコピー。通常ホームディレクトリgit clone git://github.com/sfepy/sfepy.git2. cdでsfepyフォルダに入ってCエクステンションをコンパイル。inplaceが無難。python setup.py build_ext --inplace3. インストールpython setup.py install4. テストpython ./run_tests.py↓テスト結果[111] tests/test_volume.py+++ test_volume: ok+++ test_volume_tl: ok111 test file(s) executed in 267.45 s, 0 failure(s) of 205 test(s)テスト数が前より増えたが、時間が短くなった。メモリー使用改善の効果かな。にほんブログ村
2020年06月30日
コメント(0)
-
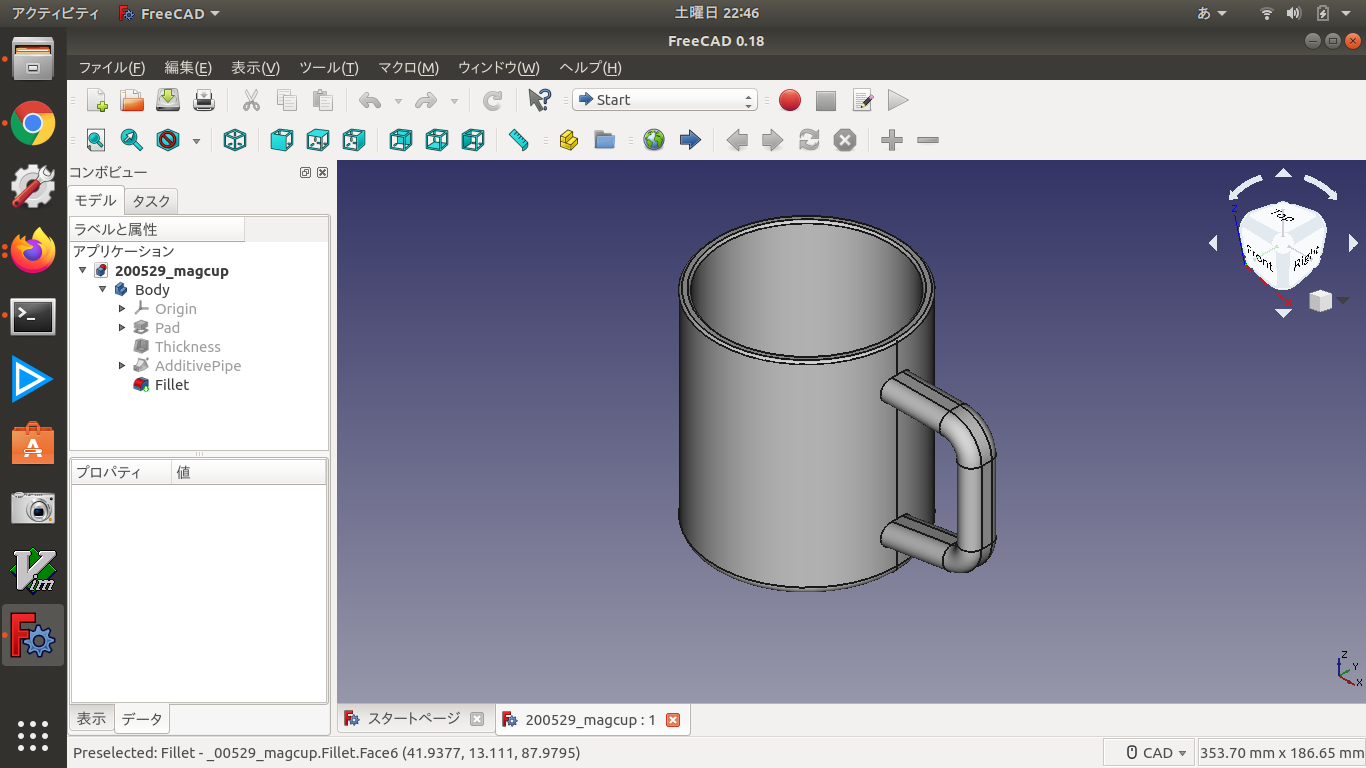
基礎からのFreeCAD
FreeCADは前から知ってはいたが、触れてこなかった。しかし、仕事でCADとの関わりが増えてきているので、試してみることにした。この本を買って、マグカップを作ってみた。取っ手を作るところで過拘束になり、苦労したが、以下のリンクのように「冗長な要素の自動削除を有効化」にチェックを入れるとできた。https://www.xsim.info/articles/FreeCAD/tutorial-mug/modeling2.html取っ手を拘束し、底の内側に2Nの荷重を与えてFEM解析してみた。FreeCADはCalculiXを内蔵している。マクロをpythonで書いたり、FreeCADをpythonモジュールとしてimportすることもできるようだ。なかなか可能性を感じさせてくれて面白そうだ。【送料無料】 基礎からのFreeCAD オープンソースの3次元CAD I / O Books 増補改訂版 / 坪田遼 【本】にほんブログ村
2020年05月30日
コメント(0)
-
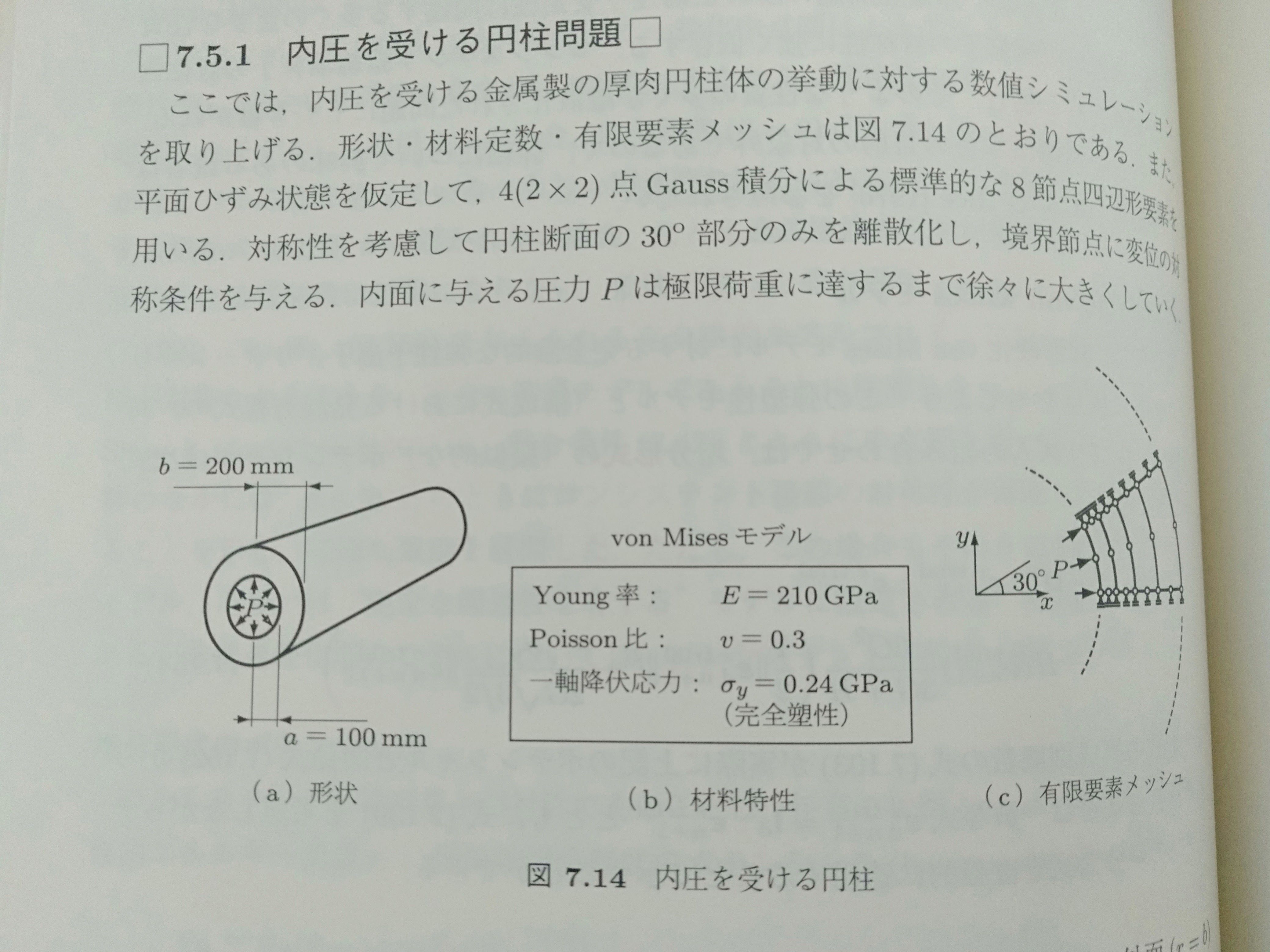
非線形有限要素法
先ほどの続き。テストに使った例題は07_5_1.dat内圧を受ける円柱の応力分布を結果ファイル07_5_1.resから確認してみた。正常に計算できていることが確認できた。周方向応力は、P=0.1GPaでは弾性であるが、P=0.18GPaでは160mmより内側の領域では塑性となっていることを示している。しかし、結果がすべて数値テキストであり、これをグラフにするのに手間がかかった。Paraviewとかで結果を視覚的に確認できないとつらい。にほんブログ村
2020年05月17日
コメント(0)
-

非線形有限要素法
第1部 基礎編(序論/テンソル解析の基礎/連続体力学と熱力学の基礎 ほか)第2部 微小ひずみ問題(数理塑性論/微小変形塑性問題の有限要素法/その他の基礎的な塑性モデルの数値計算 ほか)第3部 有限ひずみ問題(有限ひずみ超弾性体/有限ひずみ弾塑性/有限ひずみ問題における非圧縮固体材料のための有限要素 ほか)付録もう4年くらい前に買った本なのだけれど、久しぶりに手にとってみた。Ubuntu Linux で付属のソースコードをコンパイルしてテストしたら以下のエラーが出た。At line 22 of file GENERAL/fndkey.f (unit = 15, file = '07_5_1.dat')Fortran runtime error: Sequential READ or WRITE not allowed after EOF marker, possibly use REWIND or BACKSPACEError termination. Backtrace:#0 0x7f5dad45a32a#1 0x7f5dad45aed5#2 0x7f5dad45b69d#3 0x7f5dad5d495b#4 0x5561b2d34b37#5 0x5561b2d3a2fc#6 0x5561b2d197bf#7 0x5561b2d1ac3c#8 0x7f5daccd1b96#9 0x5561b2d19329#10 0xffffffffffffffffこういうところで心が折れそうになるが、"READ(NFILE,1000,END=20) INLINE"でググってみると、以下のページが見つかった。https://stackoverflow.com/questions/41791791/sequential-read-or-write-not-allowed-after-eof-markerまったく同じコードで同じように困っていた人がいた。999 RETURNの前にBACKSPACE(NFILE)を入れることで解決できた。にほんブログ村
2020年05月17日
コメント(0)
-

Sfepy Version 2020.1 released
3/31にVersion 2020.1がリリースされた。↓リリースノートhttp://sfepy.org/doc-devel/release_notes.html#id1・meshioによるメッシュフォーマットの追加、今後はPython3のみの対応などreading/writing of additional mesh formats by using meshio, Python 3 only from now on, etc.↓インストール方法http://sfepy.org/doc-devel/installation.html0. 必要なライブラリの準備 (K)Ubuntusudo apt-get install python-scipy python-matplotlib python-tables python-pyparsing libsuitesparse-dev python-setuptools mayavi2 python-dev ipython python-sympy cython python-sparseUbuntuで、ソースからビルドするのが一番確実。1. sfepyを置きたいディレクトリでgithubからコピー。通常ホームディレクトリgit clone git://github.com/sfepy/sfepy.git2. cdでsfepyフォルダに入ってCエクステンションをコンパイル。inplaceが無難。python setup.py build_ext --inplace3. インストールpython setup.py install4. テストpython ./run_tests.py↓テスト結果[105] tests/test_volume.py+++ test_volume: ok+++ test_volume_tl: ok105 test file(s) executed in 323.48 s, 0 failure(s) of 180 test(s)にほんブログ村
2020年03月31日
コメント(0)
-

Sfepy Version 2019.4 released
12/23にVersion 2019.4がリリースされた。↓リリースノートhttp://sfepy.org/doc-devel/release_notes.html#id1-1D問題でのサーフェス項のサポート-Gmshフォーマットの改善-非線形均質化法の新しい更新プロシージャ-logプロッターの改善/高速化にほんブログ村
2019年12月24日
コメント(0)
-

Sfepy Version 2019.2 released
7/2にVersion 2019.2がリリースされた。↓リリースノートhttp://sfepy.org/doc-devel/release_notes.html#id1・時間依存の均質化法の改善、Python3.7への対応などimproved support for time-dependent homogenization problems, Python 3.7 compatibility, etc.↓インストール方法http://sfepy.org/doc-devel/installation.htmlUbuntuで、ソースからビルドするのが一番確実。1. sfepyを置きたいディレクトリでgithubからコピー。通常ホームディレクトリgit clone git://github.com/sfepy/sfepy.git2. cdでsfepyフォルダに入ってCエクステンションをコンパイル。inplaceが無難。python setup.py build_ext --inplace3. インストールpython setup.py install4. テストpython ./run_tests.py↓テスト結果[105] tests/test_volume.py+++ test_volume: ok+++ test_volume_tl: ok105 test file(s) executed in 388.67 s, 0 failure(s) of 180 test(s)にほんブログ村
2019年07月03日
コメント(0)
-

Sfepy Version 2019.1 released
3/26にVersion 2019.1がリリースされた。↓リリースノートhttp://sfepy.org/doc-devel/release_notes.html#id1・線形ソルバー、二次固有値問題ソルバーなどのための自動縮退などautomatic fallback for linear solvers, quadratic eigenvalue problem solver, etc.縮退ってスーパーエレメントだろうか?にほんブログ村
2019年03月26日
コメント(0)
-

第16回オープンCAE勉強会@関東(構造など)
Salome-Meca、OpenFormなどオープンソースのCAEソフトを有効活用するための勉強会に午後から参加した。https://openfem-kanto.connpass.com/event/121600/(2) 13:00~14:30 ハンズオン勉強会Salome_Meca 2018 for Windowsの入門・初級(TFさん) →片持ちはりの例題で、Salome meca for windowsの使い方を確認。毎回、ここでsalome mecaの使い方を思い出している。(3) 14:40~17:00 研究報告会1) GetFEM++Projectコントリビューション活動状況まとめ(TKさん)→k3d-jupyter1でvtkを可視化していた。以下の記事をトレースするとブラウザ内で回転、拡大・縮小、移動できることを確認した。https://opendreamkit.org/2018/10/28/3d/3) Salome-meca2016とSalome-meca2017 for Windowsの比較(NHさん)→aster_studyになれるしかなさそうだ。4) Salome-mecaによる繰り返し熱応力解析(実験1)(TFさん)→1989年のおおがかりな実験を再現する解析。非定常な熱-構造連成解析だった。salome-mecaだとこういうことも可能なことを確認した。5) Salome-mecaによる熱応力解析(実験2)(YKさん)→鉄の丸棒に熱荷重をかけたき裂進展の解析。incrementごとの入力が大変で、pythonスクリプトで設定したということだった。にほんブログ村
2019年03月16日
コメント(0)
-

計算力学技術者試験 振動1級
無事に合格しました。去年は不覚にも落ちましたが。12月試験で、3月に通知って時間かかりすぎのような。昔は1月くらいには通知されたんだけど。-----I passed the exam of Certification Program for Computational Mechanics Engineers for Noise and Vibration of 1st grade.I failed last year. I think three months is too much to send the notice.The notice used to be sent in January previously.にほんブログ村
2019年03月05日
コメント(4)
-

第31回 設計・製造ソリューション展 DMS
3日目、最終日、担当ソフトの説明員としてブースに立った。https://www.japan-mfg.jp/ja-jp/about/dms.html大盛況で、次から次へとブースを訪れる人がいて、休む間がなかった。この展示会、何度か説明員として参加したことがあったが、こんなに忙しいのは初めてだった。展示会は手持無沙汰で立ち尽くすのが疲れるが、説明をしている間は疲れを気にする間もなく時間が過ぎていく。何人か、顔見知りのお客様が訪ねてくれた。前の職場も出展していて、懐かしい顔に会えた。PRセミナーでも製品についてしゃべった。普段、座りっぱなしで黙々と仕事をすることが多く、こんなに立ちっぱなしで、たくさんしゃべることがないので、非常に疲れたが、充実した1日だった。バーコード獲得数、アンケート獲得枚数とも目標を達成できた。ここから、見込み客に営業をかけ、少しでも多く売り上げにつながることを願うばかりだ。-----On the third day, the last day, I stood in the booth as an explanatory person for our software in charge.Since lots of people visited the exhibition, they visited our booth from one after another, and we had no time to rest.Although I had participated as an exhibitor several times in this exhibition, it was my first time to be so busy.Though it is tiring to stand on stagnation, while I am explaining, I can forget tiredness and time passing.Several visitors came to see me.I also visited the previous workplace's booth and met some nostalgic faces.At the PR seminar I also spoke about our product.As I usually work at my desk quietly, I was very tired because I kept standing and talking whole a day but it was a fulfilling day.We got achieve the target for both the bar code acquisition number and the questionnaire acquisition number. From this point, We are just hoping to open up sales for prospective customers and lead to sales as much as possible.にほんブログ村
2019年02月08日
コメント(0)
-

Sfepy Version 2018.4
2018年12月27日にVersion 2018.4がリリースされた。↓リリースノートhttp://sfepy.org/doc-devel/release_notes.html#id1・固有値解析の改善・MUMPSソルバーへのインターフェースの改善・複素数値のログとプロットの改善better support for eigenvalue problems, improved MUMPS solver interface, support for logging and plotting of complex values, etc.にほんブログ村
2019年01月12日
コメント(0)
-

計算力学技術者試験 振動1級
昨年、落ちたので再度受験した。振動関連の仕事が多いので、自分の知識レベルをチェックするために受けてみた。http://www.jsme.or.jp/cee/cmnintei.htm試験時間2時間で問題数60問。複数回答は完全回答。9分野から出題された。どうにか時間内に最後まで回答した。全体の正答率50%以上で正答率70%以上の分野が3分野以上、全問不正解の分野が2分野以下であることが合格基準。去年よりはできたような気がする。-----I took the 1st grade exam after last year's failure.Since I have a lot of vibration related work, I have tried the exam to check my knowledge level.The examination time is 2 hours and there are 60 questions.Multiple marks requires complete answers.I managed to answer to the end in time.The pass criteria is 50% or more of correct answers and three or more fields in which 70% or more are correct answers and 2 or less fields in which no correct answer.I think I did better than the last year.にほんブログ村
2018年12月15日
コメント(0)
-

第15回オープンCAE勉強会@関東(構造など)
Salome-Meca、OpenFormなどオープンソースのCAEソフトを有効活用するための勉強会に午後から参加した。https://openfem-kanto.connpass.com/event/101681/(2) 13:00~14:30 ハンズオン勉強会Salome_Meca 2018で片持ちはりの解析→aster_studyに慣れるしかない。Windows版は圧縮フォルダを解凍して、WORKフォルダのrun_salome.batを実行するだけで使える。(3) 14:40~17:00 研究報告会1) 技術書典5参加報告 Getfem++のユーザドキュメント翻訳作業(TKさん)→transifexサイトでプロジェクト立ち上げて実施中。Sphinxでhtml作成texでpdf作成linuxでtransコマンドでgoogle翻訳をコマンド実行できる。技術書典5で本を設営2) 最適化シンポジウム報告(仮)(MOさん)→音響ダイオードのトポロジー最適化など電磁場でもトポロジー最適が適用されている。3) ラズベリーパイを用いた梁の歪みの測定と解析の検証(TSさん)→ひずみゲージが600円くらいで5枚セット買えたが、2枚が破れていたらしい。正常なひずみゲージもどういうわけか動かず、うまくいかなかったということだった。総額10000円くらいだったようだ。4) 日本機械学会機械力学・計測制御部会D&C2018報告&自己紹介(仮)(jr2scqさん)→Dynamics Design Conference 2018多くの振動問題、制御問題が報告されている。D&DC2018 V_BASEフォーラム、1991年発足 1000件超の事例が保存されている。計測器収集が趣味、計測技術、計量士(一般)の資格を持っている。技術史、電気主任技術者3種、アマチュア無線4級実験モーダル解析ソフトを開発したいとのことだった。5) その他(事務連絡など)(4) 17:30~19:30 交流会(実費徴収,予約せず成り行き)→python関連の話ができて楽しかった。にほんブログ村
2018年10月20日
コメント(0)
-

クランクシャフト最適化
エンジンのクランクシャフトのウェブ形状を最適化する業務の最終報告会だった。クランクシャフトはコンロッドの並進運動を車軸への回転運動に変換する。高速回転するため、重心とモーメントを設計通りに設定しながら、ウェブ形状を変更しなければならない。この制約が厳しく、随分苦労したが、ひとまず解が出てきたのを報告した。結果は、顧客の期待通りで、納品できることになった。-----I had the last meeting with a client to report of crank shaft web shape optimization.The crank shaft converts the translate motion to rotatate motion.Since the crank shaft rotetes rapidly, the web shape should be changed maintaining the center of the gravity and the moment as the designed value.These constraints were so severe that I had a lot of strugle, but finally found a solution and report it.The result met clients' expectation and will be delivered.にほんブログ村
2018年09月19日
コメント(0)
-

Sfepy Version 2018.3 released
9/17にVersion 2018.3がリリースされた。↓リリースノートhttp://sfepy.org/doc-devel/release_notes.html#id1・変数の設定が容易になった・外形線の抽出のための新しいスクリプト↓新例題http://sfepy.org/doc-devel/examples/multi_physics/piezo_elasticity_macro.htmlhttp://sfepy.org/doc-devel/examples/multi_physics/piezo_elasticity_micro.htmlなどeasier setting of values of variables, new script for outline edge extraction, new example: homogenization of a piezoelectric heterogeneous structure, etc.にほんブログ村
2018年09月17日
コメント(0)
-

オープンCAE合同勉強会@東京2018
構造と流体の合同勉強会。前日、オープンCAE学会の総会だったので、全国から関係者が勉強会に集まった。https://opencae-kanto.connpass.com/event/86907/日時 : 2018年6月23日(土) 10:00 ~ 15:00会場 : 東洋大学白山キャンパス6号館,6201教室住所 : 東京都文京区白山5-28-20会場のマップは下記URLあるいは右欄に地図で確認下さい.http://www.toyo.ac.jp/site/access/access-hakusan.html当日スケジュール概要: ◎ 10:00 ~ 10:05 開会挨拶 ◎ 10:05~ 11:35 各地域勉強会活動報告,ディスカッション (1件15分程度、時間は目安、順不同) 関西、北東北、富山、岐阜、広島、関東流体、関東構造など ディスカッション(参加者全員) ◎ 11:35~ 12:00 研究活動紹介:流体解析に対する深層学習(yotakagi77氏) ◎ 12:00 ~ 12:40 昼休み ◎ 12:40 ~ 14:45 研究活動紹介 (1件25分程度、時間は目安、カッコ内は発表者、順不同) OpenFOAMのスレッド並列化(吉藤尚生氏(フィックスターズ)) FrontISTRの開発状況(O氏) FMI によるModelica.Thermal.FluidHeatFlow と buoyantBussinesqPimpleFoam の温度連成(finback氏) LIGGGHTS関係の話題提供(MI氏) SS400の引張試験とその再現(H氏) その他 (飛び入り話題提供があるかも)◎ 14:45 ~ 15:00 総合討論・閉会挨拶-----CAEでも機械学習、深層学習を活用しようという動きが出始めている。船舶流体力学における造波抵抗係数の推定事例が紹介されていた。船首、船尾のプロファイルデータ、オフセットデータを点群で与えて、造波抵抗係数を推定するというものだった。機械学習ライブラリはKeras/TensorFlowを使ったということだった。OpenFOAMとModelicaを連携して熱流体解析の事例も紹介された。FrontISTR 5.0αでは接触解析の反復ソルバーの対応がされたということだった。FrontISTRは反復ソルバーが充実しているということだった。SS400丸棒をもちいた室温引張試験では、関西勉強会幹事から、以下の提案があった。・上側の周方向を拘束するとくびれが出る・破断寸前の応力が下がるところは試験片の曲率をはかるとわかるかも・断面積(しぼり)も確認するといいかも勉強会に続いて、オープンCAEシンポジウム実行委員会があった。スケジュール、役割分担が決められた。終了後、はっぴ白山駅前店で懇親会だった。https://www.hotpepper.jp/strJ000979710/map/?vos=evhpppg0007&pog=mt(e)ti(kwd-43384966414)dv(c)cr(224289620570)fi()gi(26022303175)ci(422825215)lc(1009306)ps(1t1)nw(g)&gclid=EAIaIQobChMIjqmd8unq2wIVQQ4rCh3LvgIBEAAYASAAEgIfB_D_BwEにほんブログ村
2018年06月23日
コメント(0)
-

Sfepy Version 2018.2 released
6/19にVersion 2018.2がリリースされた。↓リリースノートhttp://sfepy.org/doc-devel/release_notes.html#id1・動解析の機能追加 (generalized-alpha and velocity Verlet)・流体の分散項・より速く繰り返されるプローブのための座標系参照・線形MUMPSソルバーの新ラッパーなどgeneralized-alpha and velocity Verlet elastodynamics solvers, terms for dispersion in fluids, caching of reference coordinates for faster repeated use of probes, new wrapper of MUMPS linear solver for parallel runs, etcにほんブログ村
2018年06月20日
コメント(0)
-

第14回オープンCAE勉強会@関東(構造など)
Salome-Meca、OpenFormなどオープンソースのCAEソフトを有効活用するための勉強会に参加した。(1) 10:00~12:00 フォローアップ勉強会午後のハンズオン勉強会予習会(2) 13:00~14:30 ハンズオン勉強会 Salome-Meca Aster Studyによる解析の初歩 https://www.slideshare.net/stebee19/salome-win2017-install-99915470→Salome meca for win 2017を使った片持ち梁の演習。Efficas→Aster Studyの変更、コマンドの見通しが悪くなって使いにくくなった気がする。(3) 14:40~17:00 研究報告会(発表募集中)1) getfem++ Version5.2のコンパイル方法とチュートリアル(TKさん)→タイヤの接触解析のモデル作成を紹介してくれた。解析結果が楽しみ。2) FrontISTR ver.5.0aがリリース(MOさん)→FrontISTR、会社によっては活用しているところもあるようだ。3) sfepyの動解析(TaFさん)→以下に掲載https://github.com/pyontaku14/180609_opencaemeeting/blob/master/180609_opencaemeeting_01.ipynb4) LIGGGHTSの解析例(AMさん)→粒子を使ったシミュレーションソフトの紹介https://www.cfdem.com/liggghts-open-source-discrete-element-method-particle-simulation-code5) SS400丸棒を用いた室温引張試験実施及び解析による再現(KHさん)→実験と解析を比較した事例紹介実験の様子が詳細に紹介されていた。(4) 17:30~19:30 交流会(実費徴収(3600円),別途案内)→ステーキがおいしかった。-----オープンCAEソフトを編集して、やりたいことができるようになれれば、新しい世界が開けてくるのかもしれない。にほんブログ村
2018年06月09日
コメント(0)
-

sfepy modal_analysis
1月には2次元でやったが、以下の例題を3次元のHEXAメッシュでやってみた。http://sfepy.org/doc-devel/examples/linear_elasticity/modal_analysis.html$ python examples/linear_elasticity/modal_analysis.py -d 1,1,1 -c 0,0,0 -s 8,8,8 --showsfepy: using values:sfepy: Young's modulus: 68000000000.0sfepy: Poisson's ratio: 0.36sfepy: density: 2700.0sfepy: displacement field approximation order: 1sfepy: requested 6 eigenvaluessfepy: using eigenvalue problem solver: eig.scipysfepy: method: 'eigh'sfepy: tol: 1e-05sfepy: maxiter: 1000sfepy: dimensions: [1. 1. 1.]sfepy: centre: [0. 0. 0.]sfepy: shape: [8 8 8]sfepy: generating 512 vertices...sfepy: ...donesfepy: generating 343 cells...sfepy: ...donesfepy: axis: -1sfepy: updating variables...sfepy: ...donesfepy: setting up dof connectivities...sfepy: ...done in 0.00 ssfepy: matrix shape: (1536, 1536)sfepy: assembling matrix graph...sfepy: ...done in 0.13 ssfepy: matrix structural nonzeros: 95832 (4.06e-02% fill)sfepy: updating materials...sfepy: msfepy: ...done in 0.02 ssfepy: 12 eigenvalues converged (6 ignored as rigid body modes)sfepy: number | eigenvalue | angular frequency | frequencysfepy: 1 | 7.864714548840e+07 | 8.868322585946e+03 | 1.411437376487e+03sfepy: 2 | 7.864714548840e+07 | 8.868322585946e+03 | 1.411437376487e+03sfepy: 3 | 1.451066794443e+08 | 1.204602338717e+04 | 1.917184166669e+03sfepy: 4 | 1.451066794443e+08 | 1.204602338717e+04 | 1.917184166669e+03sfepy: 5 | 1.451066794443e+08 | 1.204602338717e+04 | 1.917184166669e+03sfepy: 6 | 1.485858357801e+08 | 1.218957898289e+04 | 1.940031749336e+03sfepy: saving regions as groups...sfepy: Omegasfepy: Bottomsfepy: BottomTopsfepy: ...done1.411437376487e+03Hz1.411437376487e+03Hz1.917184166669e+03Hz1.917184166669e+03Hz1.917184166669e+03Hz1.940031749336e+03Hzちなみに同じモデルでのOptiStructの結果は以下。Subcase Mode Frequency Eigenvalue Stiffness Mass 1 7 1.355181E+03 7.250270E+07 7.250270E+07 1.000000E+00 1 8 1.355181E+03 7.250271E+07 7.250271E+07 1.000000E+00 1 9 1.796069E+03 1.273520E+08 1.273520E+08 1.000000E+00 1 10 1.796069E+03 1.273520E+08 1.273520E+08 1.000000E+00 1 11 1.796069E+03 1.273520E+08 1.273520E+08 1.000000E+00 1 12 1.893160E+03 1.414929E+08 1.414929E+08 1.000000E+00sfepyの方が固有振動数が高いが、sfepyはアイソパラメトリック要素であり、OptiStructは曲げを考慮した要素のためと考えられる。アイソパラメトリック要素には注意が必要。にほんブログ村
2018年05月04日
コメント(0)
-
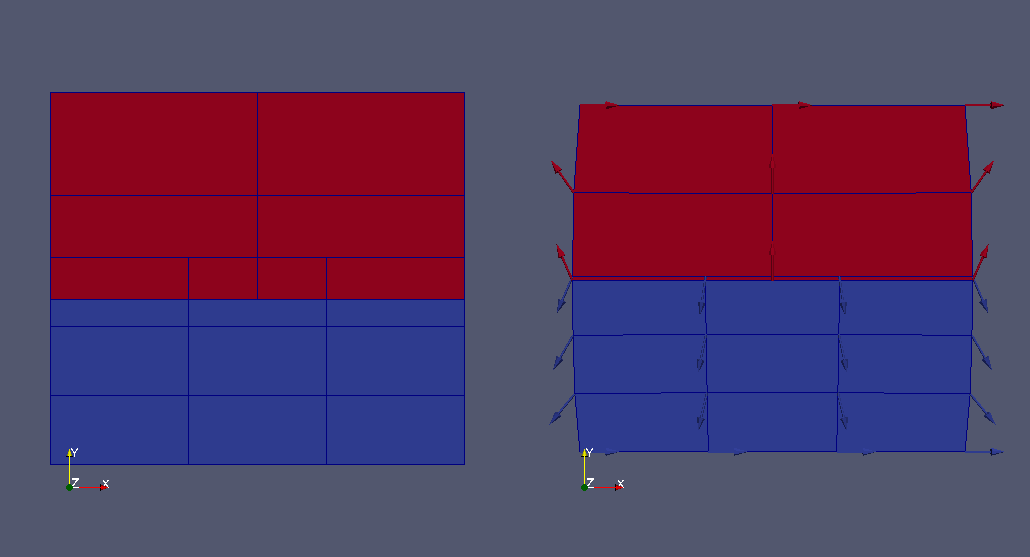
sfepy two_bodies_contact
ペナルティ法の接触の例題。http://sfepy.org/doc-devel/examples/linear_elasticity/two_bodies_contact.htmlペナルティ法は貫入した状態を接触バネによって押し戻す接触計算方法。http://www.cybernet.co.jp/ansys/glossary/sessyoku.html2物体が初期貫入した状態(左)から、貫入を解消する状態(右)になる。収束計算がlog.txtに書かれる。-----This is a penalty contact example.The penalty contact method is a method that contact spring pushes the intrusive object to resolve intrusion.This example shows the state of intrusion (left) is resolved to the state without intrusion (right). convergence calculation is written in log.txt.にほんブログ村
2018年05月03日
コメント(0)
全296件 (296件中 1-50件目)
-
-

- 楽天ブックス
- 【電子書籍PR】私立校・中高一貫校…
- (2024-11-23 22:30:09)
-
-
-

- マンガ・イラストかきさん
- 未来編更新です。十憶。
- (2024-11-23 09:05:54)
-
-
-

- ★ おすすめのビジネス書は何ですか!…
- 勝言/アスリート勝言研究会
- (2024-11-23 22:32:50)
-








