
เมื่อต้นเดือนที่ผ่านมาผมได้ร่วมแข่ง TechJam ที่ KBTG จัด และพบว่าทีม "Meow Meow :3" ผู้ชนะการแข่งขันเลือกใช้ภาษา MiniZinc ในการแก้โจทย์ปัญหา และแก้ปัญหาได้อย่างรวดเร็วเป็นทีมแรกๆ เสียด้วย
ด้วยความอยากรู้อยากเห็นเลยกลับมาศึกษาภาษานี้บ้าง และพบว่ามันเป็นภาษาที่ไม่เหมือนภาษาอื่นๆ ที่คุ้นเคยเลย การเขียนโปรแกรมจะไม่ใช่การบอกลำดับการทำงานต่างๆ ให้คอมพิวเตอร์ไปทำตามแล้ว แต่จะเปลี่ยนไปมองว่าผลลัพธ์ที่ต้องการนั้นมีข้อจำกัดอะไรบ้าง หลังจากเขียนข้อจำกัดต่างๆ จนครบก็ปล่อยให้คอมพิวเตอร์ไปคิดวิธีหาคำตอบเอาเอง
เมื่อได้ฟังหลักการทำงานแล้ว โปรแกรมเมอร์หลายๆ คนอาจรู้สึกอึดอัดขัดใจอยู่บ้าง อย่างน้อยๆ ก็ตรงที่เราจะไม่รู้ลำดับขั้นตอนการทำงานเบื้องหลังว่าโปรแกรมกำลังทำอะไรอยู่ แต่สำหรับคนที่มาจากสายอื่น ผมคิดว่า MiniZinc น่าจะช่วยตัดทอนรายละเอียดอันซับซ้อนของการเขียนโปรแกรมลงไปได้ไม่น้อยเลยทีเดียว
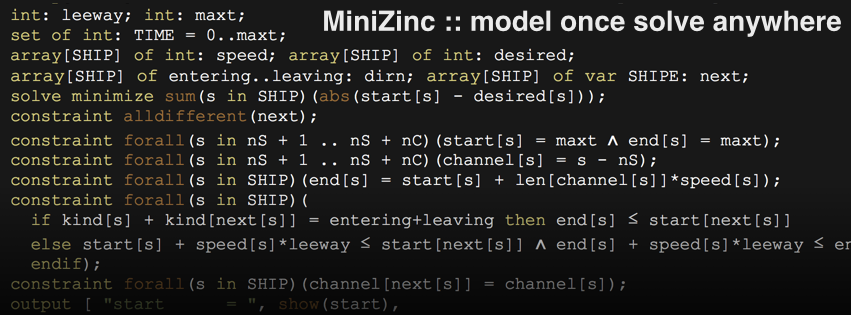
ความเป็นมาของ MiniZinc
ถ้าย้อนความกลับไปยังสมัยนักศึกษา เราอาจพอจำได้ลางๆ ว่าภาษาคอมพิวเตอร์นั้นมีด้วยกันหลายยุค ยุคแรกๆ ก็เป็นภาษาชั้นล่างที่ติดต่อกับฮาร์ดแวร์โดยตรง แล้วก็มีการพัฒนาต่อมาเรื่อยๆ จนปัจจุบันเรา (ส่วนใหญ่น่าจะ) ใช้ภาษาในยุคที่ 3-4 กันอยู่ เช่น C++, Python, JavaScript, R ซึ่งเป็นภาษาที่เราต้องป้อนคำสั่งเป็นลำดับขั้นตอนให้คอมพิวเตอร์ไปทำงานตามนั่นเอง
ส่วนภาษาคอมพิวเตอร์ในยุคที่ 5 นั้นจะซ่อนรายละเอียดปลีกย่อยที่โปรแกรมเมอร์ต้องคอยกำกับคอมพิวเตอร์ทุกขั้นตอน เปลี่ยนไปเป็นบอกว่าเราต้องการผลลัพธ์แบบไหน มีข้อจำกัดอะไรบ้างแทน โดยใช้การดำเนินการทางตรรกะมาอธิบายความสัมพันธ์และข้อจำกัดของผลลัพธ์ ภาษาในยุคนี้ที่หลายคนน่าจะเคยได้ยินชื่อก็เช่น Prolog
ด้าน MiniZinc นั้นก็เป็น ภาษาโปรแกรมเชิงข้อจำกัด ในยุคที่ 5 ที่ตั้งเป้าหมายว่าจะลดความยุ่งยากของภาษา Zinc และสร้างมาตรฐานการเขียนโปรแกรมเชิงข้อจำกัด ซึ่งมันออกเวอร์ชัน 1.0 ในปี 2009 จนถึงปัจจุบันได้เดินทางมาถึงเวอร์ชัน 2.2 แล้ว
โปรแกรมแรก!
ก่อนที่จะเจาะลึกลงไปดูรายละเอียดของคำสั่งต่างๆ เพื่อให้เขียนโปรแกรม MiniZinc แก้ปัญหาใดๆ ก็ได้ตามที่ใจต้องการ ผมคิดว่าเราควรเริ่มจากการเขียนโปรแกรมแรกอย่างรวดเร็วกันเลยดีกว่า และมันก็ไม่ควรจะเป็นเพียงแค่การพิมพ์ Hello world!
เท่านั้นด้วย เพราะเราจะมาหาคำตอบของชีวิต, เอกภพ, และทุกสิ่งทุกอย่างกัน!
โดยเราจะเริ่มจากเปิด IDE ของ MiniZinc ขึ้นมา พิมพ์โค้ดตามที่จะเห็นข้างล่างนี้ลงไป แล้วเซฟโปรแกรมในชื่อ answer.mzn
(สำหรับใครที่ขี้เกียจพิมพ์ตาม สามารถหาโค้ดทั้งหมดในบทความได้จาก Gist นี้
)

โปรแกรมเราเพิ่งเขียนเสร็จนี้มี 4 ส่วนด้วยกัน ซึ่งก็คือ
- บรรทัดแรก บอกว่าคำตอบที่ต้องการหาเป็นตัวแปรประเภทใด ซึ่งในที่นี้ก็คือจำนวนเต็ม (
int) - สี่บรรทัดถัดมาบอกข้อจำกัดต่างๆ ของคำตอบที่เราต้องการหา อันได้แก่มันจะต้องอยู่ในช่วง 1 ถึง 100 และต้องหาร 2, 3, 7 ลงตัว
- คำสั่ง
solve satisfyเป็นคำสั่งสำหรับให้โปรแกรมเริ่มทำงานค้นหาคำตอบที่ตรงตามข้อจำกัด - บรรทัดสุดท้ายเป็นการพิมพ์ผลลัพธ์ ซึ่งถ้าเราทดลองใน MiniZinc IDE ก็อาจละคำสั่งนี้ได้
เมื่อรันโปรแกรมดังกล่าวด้วยการกด Ctrl-R
ก็จะได้ผลลัพธ์กลับมาทางหน้าจอว่า 42
เป็นอันจบโปรแกรม
ขอให้จำโปรแกรมแรกของเรานี้ไว้ เพราะในหัวข้อถัดๆ ไปเราจะถอด-ประกอบ-เรียนรู้-ปรับปรุงจากมัน
รายละเอียดคำสั่ง MiniZinc
จากตัวอย่างโปรแกรมแรกของเรา แม้วากยสัมพันธ์ของ MiniZinc จะมีความแตกต่างจากภาษาที่เราคุ้นเคยในปัจจุบันพอสมควร แต่โดยหากค่อยๆ ดูไปทีละส่วนจะพบว่าไม่หนีกับภาษาอื่นเท่าใดนัก เพียงแค่เราเปลี่ยนวิธีมองหาผลลัพธ์ให้เขียนอยู่ในรูปของข้อจำกัดให้ได้ เท่านี้ก็น่าจะเบิกทางไปสู่การเขียนโปรแกรม MiniZinc ได้ไม่ยาก
รู้จักกับตัวแปร
อย่างที่ได้เห็นในโปรแกรมแรกของเราไปแล้วว่า เราสามารถประกาศตัวแปรขึ้นมาได้เลยโดยไม่ต้องกำหนดค่าตั้งต้น เพียงแค่ไปบอกว่าเราต้องการให้ตัวแปรดังกล่าวเป็นชนิดใดเท่านั้น ในการทำงานเบื้องหลังตัวแปรเหล่านี้จะถูกเปลี่ยนค่าไปเรื่อยๆ จนกว่าจะเจอค่าที่ตรงกับข้อจำกัด ซึ่งภาษา MiniZinc เรียกตัวแปรเหล่านี้ว่า "ตัวแปรตัดสินใจ" (decision variable)
แต่ยังมีตัวแปรอีกประเภทหนึ่งซึ่งไม่สามารถหรือไม่ควรเปลี่ยนค่า โดยเราอาจจะกำหนดมันขึ้นมาเพื่อย่นระยะเวลาที่ต้องพิมพ์เพราะใช้ค่านั้นบ่อยๆ ใน MiniZinc จะเรียกค่าเหล่านี้ว่า "พารามิเตอร์" (parameter) และประกาศมันได้ด้วยการตัดคำว่า var
ออกไป พร้อมทั้งกำหนดค่าให้มันผ่านเครื่องหมาย =
ในทันที ดังเช่นตัวอย่างต่อไปนี้

หรือเราอาจจะละการกำหนดค่าตั้งต้นให้พารามิเตอร์ลงไปในโค้ดโปรแกรมของเราก็ได้ ซึ่งจะทำให้ MiniZinc ถามเราซ้ำอีกทีตอนรันโปรแกรม ว่าเราต้องการให้พารามิเตอร์ที่ปล่อยว่างทิ้งไว้มีค่าเป็นเท่าไหร่ในการคำนวณครั้งนั้นๆ?
สำหรับชนิดของตัวแปรที่ MiniZinc รองรับ คือ
- จำนวนเต็ม
intมีค่าอยู่ระหว่าง ±(2 31 -2) - จำนวนจริง
floatมีค่าอยู่ระหว่าง ±(10 15 -1) โดยค่าที่เล็กที่สุดที่ทำให้สองค่าแตกต่างกันอยู่ที่ประมาณ 5×10 -324 - บูลีน
boolมีค่าเป็นtrueหรือfalse - สายอักขระ
stringสำหรับข้อความตัวอักษร -- ปัจจุบันตัวภาษายังไม่รองรับความสามารถในการแก้ปัญหาเพื่อหาข้อความตามข้อจำกัด
และจากชนิดตัวแปรข้างต้น เราสามารถนำมาสร้างเป็นตัวแปรชุดได้อีก 2 แบบ ดังนี้
- เซต
setสำหรับเก็บช่วงของค่าที่สนใจ โดยไม่สนใจตำแหน่งหรือค่าซ้ำ - อาเรย์
arrayสำหรับบอกค่าที่สนใจซึ่งผูกผันกับตำแหน่งต่างๆ ในตัวแปรชุด
ต่อไปนี้เป็นตัวอย่างการประกาศตัวแปรชุดทั้งแบบเซตและอาเรย์
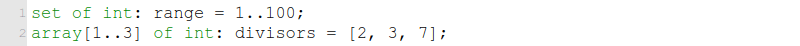
สังเกตว่าตัวแปรเซต range = 1..100
นั้น เป็นเซตของตัวเลขที่เป็นไปได้ทั้งหมดเมื่อถูกตรวจสอบด้วยข้อจำกัดแรก 1 <= answer /\ answer <= 100
ด้วยเช่นกัน MiniZinc ยอมให้เราประกาศตัวแปรโดยใช้เซตเป็นขอบเขตได้ทันที
ดังนั้น เราจึงสามารถแก้ไขโปรแกรมแรกของเราได้เป็น

เขียนข้อจำกัด
ข้อจำกัดใน MiniZinc นั้น ถ้ามองง่ายๆ ก็คงไม่ต่างจากการเขียน if-else
หรือ filter
ในภาษาที่เราคุ้นเคยเท่าใดนัก เพียงแค่เปลี่ยนตัวดำเนินการให้มีหน้าตาแบบคณิตศาสตร์มากขึ้น เช่น แทนที่จะเขียน &&
หรือ and
ก็เปลี่ยนไปเขียนด้วย /\
แทน
เราสามารถรวบสามข้อจำกัดการหารลงตัวในโปรแกรมตัวอย่างให้เหลือเพียงข้อจำกัดเดียวที่เชื่อมกันด้วย /\
ได้เช่นนี้
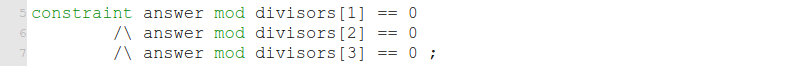
ซึ่งเราคงเห็นตั้งแต่ต้นแล้วว่า ทั้งสามพจน์ในข้อจำกัดนี้มีหน้าที่ตาเหมือนกันแทบจะทั้งหมด ส่วนที่ต่างก็เป็นเพียงตัวหารเท่านั้น ทำให้เราสามารถใช้ ตัวบ่งปริมาณทั้งหมด
forall
มาช่วยกำจัดพจน์ซ้ำๆ เหล่านั้นได้ ซึ่งจะทำให้เขียนสั้นลงเหลือเพียง
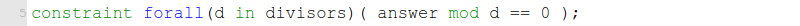
อนึ่ง สำหรับการเชื่อมกันของตัวดำเนินการแบบหรือ ( \/
) จะใช้ ตัวบ่งปริมาณบางตัว
exists
แทนนั่นเอง
หาคำตอบที่ต้องการ
การสั่ง solve satisfy
ตามโปรแกรมตัวอย่าง จะคืนคำตอบแรกที่โปรแกรมหาพบและจบการทำงานในทันที
แต่ในการแก้ กำหนดการเชิงเส้น ค่าที่เราสนใจอาจไม่ใช่ค่าใดๆ ที่พบก็ได้ แต่เป็นค่าที่สูงสุด/ต่ำสุด จากค่าทั้งหมดที่ตรงตามข้อจำกัด ซึ่งเราสามารถบอกให้ MiniZinc หาค่าที่ตรงตามเงื่อนไขดังกล่าวได้เช่นกัน
โค้ดต่อไปนี้แก้การหาคำตอบที่สนใจในโปรแกรมตัวอย่าง ซึ่งจะให้ผลลัพธ์ที่แตกต่างออกไปจากการทดลองครั้งก่อนๆ ที่ผ่านมา

พิมพ์ผลลัพธ์จัดให้สวย
สำหรับโจทย์บางข้อ การไม่ใช้คำสั่ง output
เพื่อจัดผลลัพธ์เอง ก็จะพิมพ์คำตอบออกมาได้อ่านง่ายพอสมควรอยู่แล้ว แต่หากต้องการจัดรูปแบบผลลัพธ์ ก็สามารถทำได้โดยส่งอาเรย์ของข้อความตัวอักษรเข้าไป โดยแทนที่ตัวแปรที่ต้องการแสดงด้วย \(var-name)
เช่นนี้
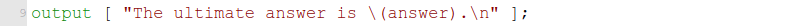
เวิร์คช็อปเพิ่มความเข้าใจ
เราได้เห็นตัวอย่างง่ายๆ ของการเขียนโปรแกรมใน MiniZinc ไปแล้ว ต่อไปนี้จะขอแนะนำโปรแกรมสำหรับแก้โจทย์ปัญหาที่น่าสนใจ พร้อมเทคนิคการเขียนโปรแกรมเพิ่มเติม
อักษรซ่อนเลข
เกมอักษรซ่อนเลข ( cryptarithmetic ) เป็นเกมที่ให้สมการ (ของเลขฐานสิบ) มาชุดหนึ่ง ซึ่งตัวเลขหลักต่างๆ ในสมการนั้นจะถูกแทนที่ด้วยตัวอักษร คำถามคือให้หาว่าตัวอักษรแต่ละตัวมีค่าเป็นเท่าใดบ้าง โดยตัวอักษรที่ไม่เหมือนกันจะต้องมีค่าไม่ซ้ำกันด้วย
ตัวอย่างเช่นสมการ SEND + MORE = MONEY
นั้นมีค่าเท่ากับ 9567 + 1085 = 10652
นั่นเอง
ซึ่งเราสามารถเขียนเป็นโปรแกรมให้ MiniZinc ไปแก้ปริศนาได้ดังนี้

ส่วนที่น่าสนใจในโปรแกรมนี้ คือบรรทัดที่ 10-11 ที่เช็คว่าตัวอักษรแต่ละตัวต้องมีค่าไม่ซ้ำกัน
จะเห็นว่าเราสร้างตัวแปรเพิ่มขึ้นมาเพื่อใช้คำนวณข้อจำกัดนี้เพียงข้อเดียว หากเทียบกับการเขียนโปรแกรมโดยทั่วไปแล้ว ก็คงคล้ายกับการประกาศตัวแปรที่ระดับ global นั่นเอง
นี่ไม่ใช่การเขียนโปรแกรมที่ดีเท่าใดนัก และเราสามารถปรับปรุงมันได้โดยการสร้างเพรดิเคต ( predicate ) ซึ่งเปรียบได้กับการเขียนฟังก์ชันที่รับตัวแปรต่างๆ แล้วตอบกลับเป็นบูลีนว่าถูกหรือผิดตามข้อจำกัดที่สนใจ
เราสามารถเปลี่ยนโค้ดข้างต้นให้อยู่ในรูปของเพรดิเคตได้ ดังนี้

อนึ่ง สังเกตว่าเราใช้ตรรกะ "เมื่อและก็ต่อเมื่อ" ( iff ) เพื่อรับรองว่าสองข้างของตัวเชื่อมจะต้องเป็นจริงพร้อมกันหรือเท็จพร้อมกันเท่านั้น นี่เทียบได้กับเกต XNOR นั่นเอง
ซูโดกุ
เชื่อว่าคงไม่มีใครไม่รู้จักเกม ซูโดกุ
จากความรู้ MiniZinc ที่ผ่านๆ มา เราอาจเขียนโปรแกรมแก้โจทย์ซูโดกุที่เราสนใจข้อหนึ่งออกมาเป็นไฟล์ sudoku-solver.mzn
ได้ดังนี้

แม้เราจะสามารถเขียนข้อจำกัดของปัญหาได้สั้นกระชับเข้าใจง่าย แต่ส่วนที่ยุ่งเหยิงที่สุดในโปรแกรมกลับกลายเป็นการป้อนข้อมูลแทน สำหรับโจทย์ข้อนี้นอกจากข้อมูลนำเข้าจะยืดยาวแล้ว การค่อยๆ ป้อนตัวเลขตำแหน่งต่างๆ ในตารางทีละตัวยังเสี่ยงต่อการพิมพ์ผิดอีกด้วย
เราอาจแก้โปรแกรมข้างต้น โดยเปลี่ยนบรรทัดที่เป็น constraint t[r,c] = x;
ทั้งหมด ไปเป็นพารามิเตอร์ตารางตั้งต้น (ใส่เลข 0 แทนช่องที่ต้องการแก้โจทย์หาตัวเลข) พร้อมเพิ่มกฎการห้ามเปลี่ยนตัวเลขในตารางตั้งต้นที่ไม่ใช่เลข 0 เช่นนี้

ถึงนี่จะดูง่ายขึ้นมากแล้ว แต่มันก็ยังมีข้อเสียตรงที่ข้อมูลต่างๆ นั้นผูกติดแนบแน่นไปกับไฟล์โปรแกรมของเราอยู่ดี หากเราต้องการแก้โจทย์ซูโดกุเกมอื่น ก็ต้องทำสำเนาไฟล์นี้แล้วค่อยๆ เปลี่ยนค่าตัวเลขในตัวแปร s
เอา ทั้งที่ส่วนตรรกะโปรแกรมไม่ได้เปลี่ยนเลยแม้แต่นิดเดียว
ทางออกสำหรับปัญหานี้ คือแยกพารามิเตอร์เฉพาะตัวของโจทย์ข้อนั้นๆ ไปไว้ในไฟล์ .dzn
ที่ MiniZinc จัดเตรียมไว้ให้ ซึ่งก็คือ เราจะสร้างไฟล์ sudoku-input-1.dzn
ขึ้นมา โดยมีเนื้อหาดังนี้

ส่วนที่ไฟล์โปรแกรม sudoku-solver.mzn
ก็จะลบค่าพารามิเตอร์ตั้งต้นของ s
ทิ้งไป เหลือไว้แค่การประกาศชนิดตัวแปรของ s
เท่านั้นพอ
ทั้งนี้ทั้งนั้น ก่อนจะเริ่มรันโปรแกรมดังกล่าว (หรือโปรแกรมอื่นใดที่รับข้อมูลนำเข้าเป็นไฟล์) ก็อย่าลืมไปแก้ Configuration
ใน IDE ให้ค่าของ Data file
ชี้ไปยัง sudoku-input-1.dzn
ด้วยนะ
จัดกระเป๋าเดินทาง
ปัญหาการจัดกระเป๋าเดินทาง ( knapsack problem ) กล่าวว่า ให้กระเป๋าเดินทางที่บรรจุน้ำหนักได้จำกัดที่ค่าหนึ่ง และของอีกหลายๆ ชิ้นซึ่งแต่ละชิ้นมีน้ำหนักและมูลค่าแตกต่างกันไป ถามว่าต้องเลือกหยิบของชิ้นใดใส่กระเป๋าบ้าง เพื่อให้ได้มูลค่ารวมของสิ่งของสูงสุด โดยน้ำหนักของสิ่งของที่เลือกต้องไม่เกินน้ำหนักที่กระเป๋าจะรับได้
ปัญหาดังกล่าวสามารถแปลงเป็นข้อจำกัดใน MiniZinc ได้ดังนี้

ข้อมูลตัวอย่างสำหรับปัญหาการจัดกระเป๋าเดินทาง ที่มีสิ่งของให้ตัดสินใจ 42 ชิ้น

จากเวลาคำนวณ 12 นาที ผมเข้าใจว่า MiniZinc น่าจะทดลองหยิบของด้วยทุกวิธีที่เป็นไปได้ จนมั่นใจในคำตอบสุดท้ายว่าการหยิบของที่ดีที่สุดคือ
knapsack = {1,8,9,10,12,15,16,20,21,22,24,25,27,29,32,33,34,38};
กำหนดการจำนวนเต็ม
สมมติว่าเราเปิดร้านอาหารแห่งหนึ่ง ซึ่งประกอบไปด้วย 2 เมนูด้วยกัน คือ
- แซลมอนซาซิมิ ราคา 129 บาท วัตถุดิบคือปลาแซลมอน 120 กรัม
- แซลมอนซูชิ ราคา 19 บาท วัตถุดิบคือปลาแซลมอน 15 กรัม และข้าว 10 กรัม
เราต้องการหา ว่าการขายอาหารแต่ละเมนูเป็นจำนวนเท่าใด ถึงจะให้รายได้สูงที่สุด?
หากตอนเริ่มต้นของวันเรามีวัตถุดิบคือแซลมอน 5 กิโลกรัม และข้าว 2 กิโลกรัม เมื่อนำเงื่อนไขต่างๆ มาเขียนมาเขียนเป็นระบบอสมการ จะได้
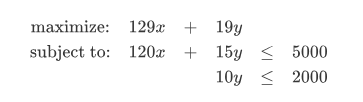
เมื่อพล็อตระบบอสมการออกมาดู ก็จะเห็นหน้าตาของบริเวณที่เป็นไปได้ ( feasible region ) ซึ่งก็คือบริเวณที่อยู่ด้านใต้ของเส้นทุกเส้น (ยกเว้นเส้นแกน) เช่นนี้
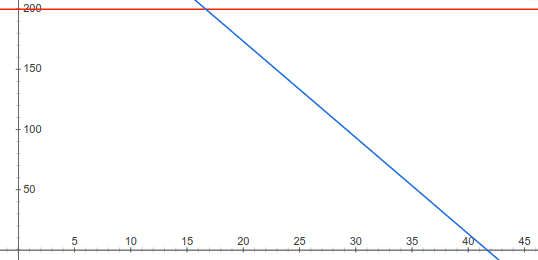
เส้นสีน้ำเงินแทนอสมการแรก และเส้นสีแดงแทนอสมการที่สอง
แน่นอนว่าเราคงไม่ขายอาหารแค่ครั้งละครึ่งจาน เราจึงต้องหาคำตอบด้วยกำหนดการจำนวนเต็ม ( integer programming ) ซึ่งสามารถเขียนเป็นโปรแกรมได้ดังนี้

ซึ่งจะให้คำตอบว่า เราควรขายซาซิมิ 17 ชุด และซูชิ 197 คำ ซึ่งจะทำให้มีรายรับสูงที่สุดที่ 5,936 บาท
สรุป
จากตัวอย่างต่างๆ ที่ได้เห็นกันไปนั้น แม้ MiniZinc จะไม่ได้เลือกอัลกอริทึมที่รวดเร็วที่สุดมาแก้ปัญหาก็ตาม แต่ด้วยไวยกรณ์และวากยสัมพันธ์ของมัน ก็ทำให้การเขียนโปรแกรมเพื่อตรวจสอบโมเดลทางคณิตศาสตร์ต่างๆ เป็นไปได้อย่างเรียบง่าย รวดเร็ว และลดข้อผิดพลาดต่างๆ ที่พบเจอได้ง่ายในภาษายุคเก่า
นอกจากนี้ การที่ตัวภาษาซ่อนรายละเอียดทางเทคนิคโปรแกรมมิ่งไปเกือบหมด และเลือกแต่ส่วนที่เป็นตรรกะคณิตศาสตร์พื้นฐานมาให้ใช้ ก็น่าจะทำให้ผู้ที่ไม่ได้มีพื้นด้านการเขียนโปรแกรมมาก่อน สามารถสร้างโมเดลทางคณิตศาสตร์ได้ง่ายขึ้นด้วย ซึ่งผมคิดว่านี่คือประโยชน์ที่แท้จริง เพราะเราสามารถนำมันไปใช้แก้ปัญหาต่างๆ ในโลกจริงได้อย่างมากมาย
สำหรับนักพัฒนาที่เชี่ยวชาญอัลกอริทึมแล้ว แม้ว่า MiniZinc จะไม่ได้ช่วยให้เขียนโปรแกรมที่ทำงานได้เร็วขึ้นก็ตาม แต่ผมคิดว่าการเขียนโปรแกรมในยุคที่ 5 ที่เป็นเชิงตรรกะและข้อจำกัด ก็เป็นแนวคิดที่มีคุณค่าให้ศึกษาไม่น้อยเลยทีเดียว ยิ่งเมื่อดูคู่ไปกับเทรนด์ปัญญาประดิษฐ์แล้ว นี่น่าจะเป็นอนาคตของการเขียนโปรแกรมในยุคหน้าอย่างแน่นอน











Comments
น่าสนใจมาก ขอบคุณครับ
+1 ขอบคุณด้วย
ขอบคุณครับ น่าสนใจมาก
แจ่มแมวเลยครับต้องลองศึกษาดูบ้างละ
น่าสนใจจนต้องโหลดมาลองเลยครับ
ขอบคุณสำหรับข้อมูลที่แบ่งปันครับ
วากยสัมพันธ์ ...
สะดุดกับคำนี้เหมือนกัน .... ไม่ได้เห็นนานมาก ดูจากรูปประโยชน์มันน่าจะคือ syntax ป่ะฮะ
นับถือในความพยายามอธิบาย เข้าใจง่ายมากครับ ขอบคุณครับ
เทคโนโลยีไม่ผิด คนใช้มันในทางที่ผิดนั่นแหละที่ผิด!?!
+1
ผมลืมขอบคุณ ขอบคุณ @neizod ด้วยครับที่ตั้งใจเขียนมาให้อ่าน
ได้ความรู้ดีครับ เหมือนย่อยข่าวไปในตัวด้วย
เห็นอนาคตเลย อีกหน่อยไม่ต้องมีโปรแกรมเมอร์แล้ว
นึกถึง Prolog แฮะ
blog.semicolon.in.th
น่าสนใจครับ จะลองไปศึกษาดู
ขอบคุณสำหรับบทความดี ๆ ครับ...