あの数式のところで色んなことができるけど、ほんとに便利だよね
大学のレポートを作るときなんか数式が分かんなくて大変な思いしたよ...
そもそもスプレッドシートの数式ってプログラムの上ではどうやって扱われているんだろう
あーしの 車輪の再発明シリーズ として、「自分で設計・実装するならこうかな!」っていうのを記事にしたいと思います
「あるもの使えば良いじゃん」って言われちゃうかもだけど、自分でもやってみたいんだ
↓
で早速だけど、数式をデータとしてどうやって保持するかなんだけど、
大学4年生のときに習った「 木構造」ってのが使えるはずなんだ
この木構造、すっごく奥が深いから、また別の記事で紹介したいんだけど、
その中で「 AST」っていうのがあって、これで上手く数式を表現できるはず
ASTっていうのは Abstract Syntax Tree(抽象構文木)の略称で、
例えば「1/(X1+X2)」みたいな数式があれば、
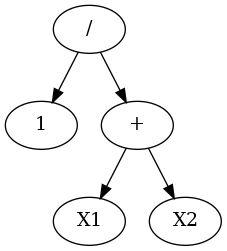
こんな木構造になって、
「IF(X1+X2>=10, Y1, Y2)」みたいな数式のときは、
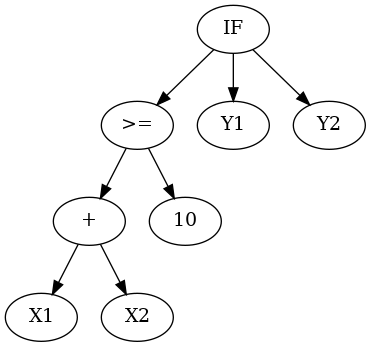
こんな風な木構造で表されるよ
丸で囲われているところを ノード(Node)、矢印を エッジ(Edge)って言って、
あと1つ目の図の「1」と「X1」、「X2」みたいにそれ以上、分岐していないノードを リーフノード(Leaf Node)って言うんだ
それぞれ一番深い、下のリーフノードから処理していく感じで考えてほしくて、
「1/(X1+X2)」の例だと
?@ X1とX2を「+」して
?A 1と↑の?@の結果を「/」して..
みたいな順序だよ
Pythonを使って図を作ってるんだけど
shell
$
pip install graphviz
で、graphvizをインストールして、
Python
from graphviz import Digraph
dot = Digraph()
# ノードを追加(AからHは記号みたいなものだよ )
)
dot.node('A', 'IF')
dot.node('B', '>=')
dot.node('C', '+')
dot.node('D', 'X1')
dot.node('E', 'X2')
dot.node('F', '10')
dot.node('G', 'Y1')
dot.node('H', 'Y2')
# エッジを追加( で定義したノードとノードの関係を書いていくよ
で定義したノードとノードの関係を書いていくよ )
)
dot.edge('A', 'B')
dot.edge('A', 'G')
dot.edge('A', 'H')
dot.edge('B', 'C')
dot.edge('B', 'F')
dot.edge('C', 'D')
dot.edge('C', 'E')
# PNGファイルとしてグラフを出力
dot.render('image', format='png', cleanup=True)
こんな感じのコードで、一つずつノードとノードの関係を定義していって、最後のrenderメソッドでファイルを作成してるよ
けどこれが結構大変で
「IF(X1+X2>=10, Y1, Y2)」みたいな数式が与えられたら、上手く処理して自動でASTを作りたいよね
(その辺りは次の記事で
この記事では、ASTというデータ構造を紹介してみたよ、導入だね
次の記事で「数式を解釈してASTを作成」、
その次くらいの記事で「ASTにもとづいて式を評価」、
こんな感じでゆるくやっていければなと思ってます
以下はアフィリエイトのリンクなので、嫌いな人は書籍名などで検索してみてください
紹介したASTや木構造っていうのは、離散数理っていう分野のグラフ理論で出てくる考え方なんだけど、
工学基礎 離散数学とその応用
に色々な応用がジュニアの方にも分かりやすく書かれてるから、おすすめです
お世話になった茨木先生の離散数理の本もできれば紹介したいんだけど、気づいたら絶版になってた