Math solver ( `MathSolver` ) structured data

To help students, teachers, and others with math problems, you can use structured data to indicate the type of math problems and links to step-by-step walkthroughs for specific math problems. Here's an example of how math solvers may look in Google Search results (the appearance is subject to change):

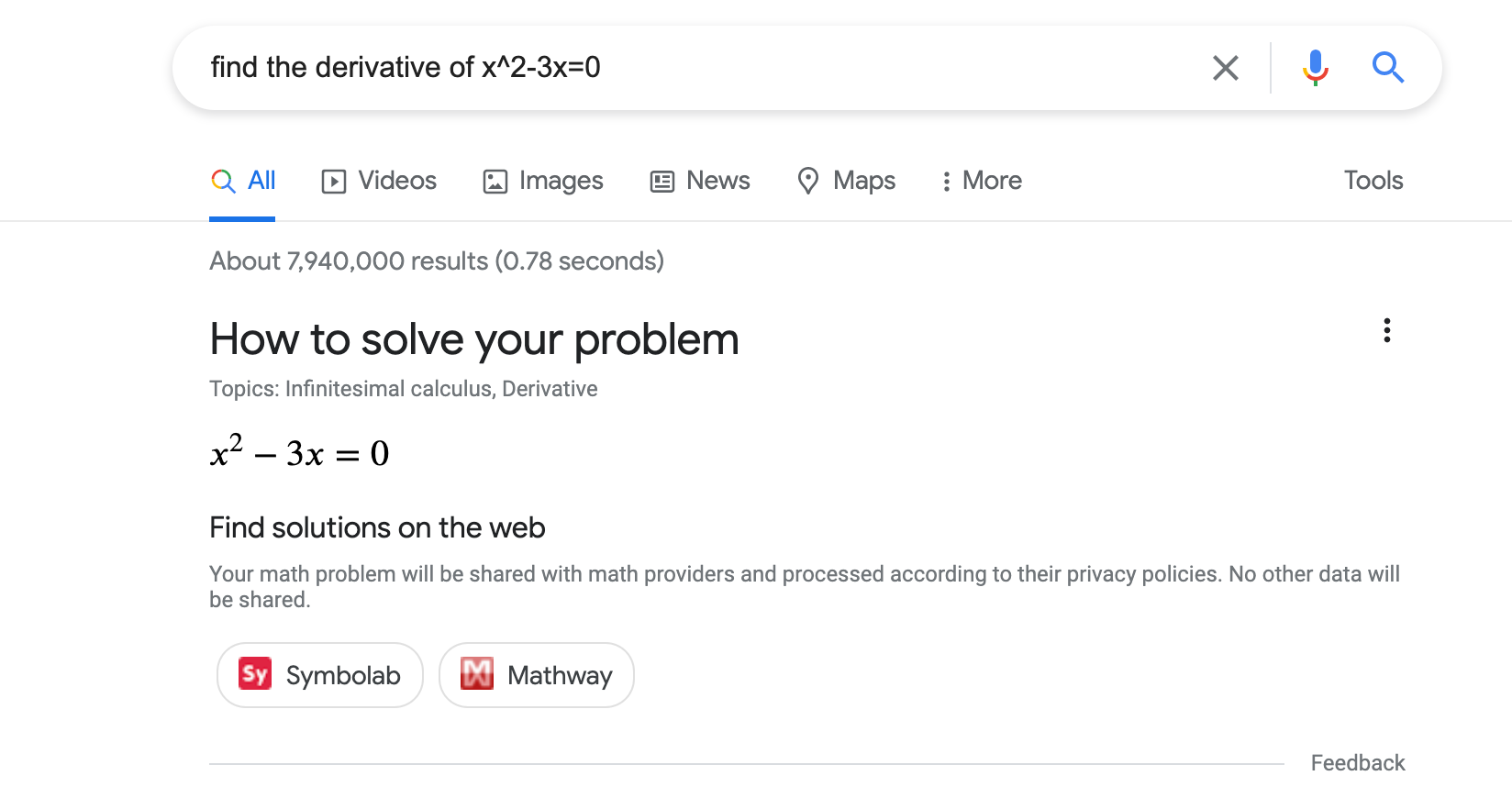
$Example of a math solvers rich result$

How to add structured data

Structured data is a standardized format for providing information about a page and classifying the page content. If you're new to structured data, you can learn more about how structured data works .

Here's an overview of how to build, test, and release structured data.

Add the required properties . Based on the format you're using, learn where to insert structured data on the page .
Using a CMS? It may be easier to use a plugin that's integrated into your CMS.
Using JavaScript? Learn how to generate structured data with JavaScript .
Follow the guidelines .
Validate your code using the Rich Results Test and fix any critical errors. Consider also fixing any non-critical issues that may be flagged in the tool, as they can help improve the quality of your structured data (however, this isn't necessary to be eligible for rich results).
Deploy a few pages that include your structured data and use the URL Inspection tool to test how Google sees the page. Be sure that your page is accessible to Google and not blocked by a robots.txt file, the noindex tag, or login requirements. If the page looks okay, you can ask Google to recrawl your URLs .
Note : Allow time for re-crawling and re-indexing. Remember that it may take several days after publishing a page for Google to find and crawl it.
To keep Google informed of future changes, we recommend that you submit a sitemap . You can automate this with the Search Console Sitemap API .

Examples

One solver action

Here's an example of a math solver home page that has one solver action that can solve polynomial equations and derivative problems and is available in English and Spanish.

<html>
<head>
<title>An awesome math solver</title>
</head>
<body>
<script type="application/ld+json">
[
  {
    "@context": "https://schema.org",
    "@type": ["MathSolver", "LearningResource"],
    "name": "An awesome math solver",
    "url": "https://www.mathdomain.com/",
    "usageInfo": "https://www.mathdomain.com/privacy",
    "inLanguage": "en",
    "potentialAction": [{
      "@type": "SolveMathAction",
      "target": "https://mathdomain.com/solve?q={math_expression_string}",
      "mathExpression-input": "required name=math_expression_string",
      "eduQuestionType": ["Polynomial Equation","Derivative"]
     }],
    "learningResourceType": "Math solver"
  },
  {
    "@context": "https://schema.org",
    "@type": ["MathSolver", "LearningResource"],
    "name": "Un solucionador de matemáticas increíble",
    "url": "https://es.mathdomain.com/",
    "usageInfo": "https://es.mathdomain.com/privacy",
    "inLanguage": "es",
    "potentialAction": [{
      "@type": "SolveMathAction",
      "target": "https://es.mathdomain.com/solve?q={math_expression_string}",
      "mathExpression-input": "required name=math_expression_string",
      "eduQuestionType": ["Polynomial Equation","Derivative"]
     }],
    "learningResourceType": "Math solver"
  }
]
</script>
</body>
</html>

<html>
<head>
<title>An awesome math solver</title>
</head>
<body>
<script type="application/ld+json">
[
  {
    "@context": "https://schema.org",
    "@type": ["MathSolver", "LearningResource"],
    "name": "An awesome math solver",
    "url": "https://www.mathdomain.com/",
    "usageInfo": "https://www.mathdomain.com/privacy",
    "inLanguage": "en",
    "potentialAction": [{
      "@type": "SolveMathAction",
      "target": "https://mathdomain.com/solve?q={math_expression_string}",
      "mathExpression-input": "required name=math_expression_string",
      "eduQuestionType": ["Polynomial Equation","Derivative"]
     }],
    "learningResourceType": "Math solver"
  },
  {
    "@context": "https://schema.org",
    "@type": ["MathSolver", "LearningResource"],
    "name": "Un solucionador de matemáticas increíble",
    "url": "https://es.mathdomain.com/",
    "usageInfo": "https://es.mathdomain.com/privacy",
    "inLanguage": "es",
    "potentialAction": [{
      "@type": "SolveMathAction",
      "target": "https://es.mathdomain.com/solve?q={math_expression_string}",
      "mathExpression-input": "required name=math_expression_string",
      "eduQuestionType": ["Polynomial Equation","Derivative"]
     }],
    "learningResourceType": "Math solver"
  }
]
</script>
</body>
</html>

The Spanish markup could be placed directly on https://es.mathdomain.com/ instead of placing it alongside the English version of the math solver markup.

Two solver actions

Here's an example of a math solver home page that has two solver endpoints: one endpoint can solve polynomial equations and the other endpoint can solve trigonometric equations. It is available only in English.

<html>
<head>
<title>An awesome math solver</title>
</head>
<body>
<script type="application/ld+json">
{
  "@context": "https://schema.org",
  "@type": ["MathSolver", "LearningResource"],
  "name": "An awesome math solver",
  "url": "https://www.mathdomain.com/",
  "usageInfo": "https://www.mathdomain.com/privacy",
  "inLanguage": "en",
  "potentialAction": [{
     "@type": "SolveMathAction",
     "target": "https://mathdomain.com/solve?q={math_expression_string}",
     "mathExpression-input": "required name=math_expression_string",
     "eduQuestionType": "Polynomial Equation"
   },
   {
     "@type": "SolveMathAction",
     "target": "https://mathdomain.com/trig?q={math_expression_string}",
     "mathExpression-input": "required name=math_expression_string",
     "eduQuestionType": "Trigonometric Equation"
   }],
  "learningResourceType": "Math solver"
}
</script>
</body>
</html>

Guidelines

For your page to be eligible for math solver rich results, you must follow these guidelines:

Technical Guidelines

Add MathSolver structured data to the home page of your site.
Ensure that Googlebot can crawl your site efficiently .
If you have several identical copies of the same math solver hosted under different URLs, use the canonical URLs on each copy of the page.
We don't allow math solvers that are entirely hidden behind a login or paywall. Once users navigate from the feature on Google to your site, the solution and a step-by-step walkthrough for their initial problem must be accessible to them. Additional content can be behind a login or paywall.

Content guidelines

We created these Math Solver content guidelines to ensure that our users are connected with learning resources that are relevant. If we find content that violates these policies, we'll respond appropriately, which may include taking manual action and removing your pages from appearing in the math solver experience on Google.

We don't allow promotional content disguised as a math solver, such as those posted by a third party (for example, affiliate programs ).
You are responsible for the accuracy and quality of your math solver through this feature. If a certain amount of your data is found to be inaccurate based on our quality review processes, then your solver may be removed from the feature until you resolve the issues depending on the severity. This applies to:
- The accuracy of the problem types your solver is capable of solving.
- The accuracy of your solutions for math problems your solver declares it can solve.

Structured data type definitions

You must include the required properties for your content to be eligible for display as a rich result. You can also include the recommended properties to add more information to your structured data, which could provide a better user experience.

MathSolver

A MathSolver is a tool that assists students, teachers, and others with math problems by laying out step-by-step solutions. Use MathSolver structured data on your site's home page.

The full definition of MathSolver is available at schema.org/MathSolver .

The Google-supported properties are the following:

Required properties

potentialAction

SolveMathAction

The action that leads to a mathematical explanation (for example, step-by-step solution or graph) of a math expression.

 { 
 "@type" 
 : 
  
 "MathSolver" 
 , 
 "potentialAction" 
 : 
  
 [{ 
  
 "@type" 
 : 
  
 "SolveMathAction" 
 , 
  
 "target" 
 : 
  
 "https://mathdomain.com/solve?q={math_expression_string}" 
 , 
  
 "mathExpression-input" 
 : 
  
 "required name=math_expression_string" 
 , 
  
 "eduQuestionType" 
 : 
  
 "Polynomial Equation" 
  
 }] 
 }

potentialAction.mathExpression-input

Text

A placeholder for a mathematical expression (for example: x^2-3x=0) that is sent by Google to your website. You can then "solve" the math expression, which may involve simplifying, transforming, or solving for a specific variable. The string can take many formats (for example: LaTeX, Ascii-Math, or mathematical expressions that you can write with a keyboard).

mathExpression-input is an annotated property. See the Potential Actions page for more information.

For some problem types, the math_expression_string indicates both the problem type and parameters of the problem type. Here are some examples of the more complicated problem types so that you can anticipate and parse them correctly.

Derivatives

Google will send a math_expression_string in one of two forms:

```
 ( 
  math_expression 
 
 ) 
 ' 
```

 d 
 / 
 d variable 
 
  
  math_expression

Examples :

( x ^ 2 + x ) '

d / dx ( x ^ 2 + x )

d / dy y ^ 2 + y

Integrals

Google will send a math_expression_string in one of two forms :

```
\ int 
  
  math_expression 
 
```

\int_{ from 
}^{ to 
} math_expression

Examples:

\int x^2+x
\int_{0}^{2} x^2+x

Limits

Google will send a math_expression_string in one of two forms:

```
\lim math_expression 
```

\ lim_ 
 { 
  variable 
 
\ rightarrow value 
 
 } 
  
  math_expression

Examples:

\lim_{x\rightarrow0} sin(x)/x
\lim_{y\rightarrow\infty} sin(y)/y
\lim sin(x)/x

url

URL

The URL of the MathSolver .

usageInfo

URL

The privacy policy for your math problem solving site.

 { 
  
 "@type" 
 : 
  
 "MathSolver" 
 , 
  
  "usageInfo" 
 : 
  
 "https://www.mathdomain.com/privacy" 
 }

potentialAction.target

EntryPoint

The URL target entrypoint for an action. The potentialAction.target property accepts a string to represent the math expression that's being solved by the action.

 { 
 "@type" 
 : 
  
 "MathSolver" 
 , 
 "potentialAction" 
 : 
  
 [{ 
  
 "@type" 
 : 
  
 "SolveMathAction" 
 , 
  
  "target" 
 : 
  
 "https://mathdomain.com/solve?q={math_expression_string}" 
  
 }] 
 }

Recommended properties

Recommended properties
`inLanguage`	`Text` The language(s) that are supported by your math problem solving site. See this table for a list of possible languages. { "@type" : "MathSolver" , "inLanguage" : "es" }
`assesses`	`Text` list of Problem Type Definitions The problem type(s) that are solved with the `HowTo` . Use the `assesses` property if you're using `HowTo` markup in addition to `MathSolver` markup. { "@type" : "MathSolver" , "assesses" : "Polynomial Equation" }
`potentialAction.eduQuestionType`	`Text` list of Problem Type Definitions The problem type(s) that are capable of being solved by the `potentialAction.target` property. { "@type" : "SolveMathAction" , "eduQuestionType" : "Polynomial Equation" }

inLanguage

Text

The language(s) that are supported by your math problem solving site. See this table for a list of possible languages.

 { 
  
 "@type" 
 : 
  
 "MathSolver" 
 , 
  
  "inLanguage" 
 : 
  
 "es" 
 }

assesses

Text list of Problem Type Definitions

The problem type(s) that are solved with the HowTo . Use the assesses property if you're using HowTo markup in addition to MathSolver markup.

 { 
  
 "@type" 
 : 
  
 "MathSolver" 
 , 
  
  "assesses" 
 : 
  
 "Polynomial Equation" 
 }

potentialAction.eduQuestionType

Text list of Problem Type Definitions

The problem type(s) that are capable of being solved by the potentialAction.target property.

 { 
  
 "@type" 
 : 
  
 "SolveMathAction" 
 , 
  
  "eduQuestionType" 
 : 
  
 "Polynomial Equation" 
 }

LearningResource

A LearningResource indicates that the subject of the markup is a resource that assists students, teachers, and others with educational learning. Use LearningResource on your site's home page.

The full definition of LearningResource is available at schema.org/LearningResource .

The Google-supported properties are the following:

Required properties

Required properties
`learningResourceType`	`Text` The type of this learning resource. Use this fixed value: `Math Solver` . { "@type" : [ "MathSolver" , "LearningResource" ], "learningResourceType" : "Math Solver" }

learningResourceType

Text

The type of this learning resource. Use this fixed value: Math Solver .

 { 
  
 "@type" 
 : 
  
 [ 
 "MathSolver" 
 , 
  
 "LearningResource" 
 ], 
  
  "learningResourceType" 
 : 
  
 "Math Solver" 
 }

Problem Type Definitions

Use the following list of problem types as either the eduQuestionType for a MathSolver.potentialAction or for the assesses field of a MathSolver when the MathSolver is accompanying a HowTo that walks through a specific math problem.

The following table shows some examples for the problem types you can annotate:

Example problem types (this isn't an exhaustive list)

Absolute Value Equation

Absolute value equations. For example: |x - 5| = 9

Algebra

A generic problem type that can be placed with other problem type. For example: polynomial equations, exponential equations, and radical expressions.

Arc Length

Arc length problems. For example: Determine the length of x = 4 (3 + y)^2, 1 < y < 4.

Arithmetic

Arithmetic problems. For example: Find the sum of 5 + 7.

Biquadratic Equation

Biquadratic equations. For example: x^4 - x^2 - 2 = 0.

Calculus

A generic problem type that can be placed with other problem types. For example: integrals, derivatives, and differential equations.

Characteristic Polynomial

Find the characteristic polynomial of {{1,2,5}, {3,-1,1}, {1,2,3}} .

Circle

Circle related problems. For example: Find the radius of x^2 + y^2 = 3.

Derivative

Derivative of 5x^4 + 2x^3 + 4x - 2.

Differential Equation

Differential equation problems. For example: y+dy/dx=5x.

Distance

Distance problems. For example: Find the distance between (6,-1) and (-3,2).

Eigenvalue

Eigenvalue problems. For example: Find the eigenvalues for the matrix [[-6, 3], [4, 5]].

Eigenvector

Eigenvector problems. For example: Find the eigenvector for the matrix [[-6, 3], [4, 5]] with eigenvalues of [-7, 6].

Ellipse

Ellipse problems. For example: Find the x and y intercepts of 9x^2 + 4y^2 = 36.

Exponential Equation

Exponential equations. For example: 7^x = 9.

Function

Polynomial simplifications. For example: (x-5)^2 * (x+5)^2.

Function Composition

f(g(x)) when f(x)=x^2-2x, g(x)=2x-2

Geometry

A generic problem type that can be placed with other problem types. For example: circle, ellipse, parabola, slope.

Hyperbola

Hyperbola problems. For example: Find the x-intercept of (x^2)/4 - (y^2)/5 = 1.

Inflection Point

Find the inflection point of f(x) = 1/2x^4 +x^3 - 6x^2.

Integral

Integral of sqrt (x^2 - y^2).

Intercept

Line intercept problems. For example: Find the x-intercept of the line y = 10x - 5.

Limit

Limit problems. For example: Find the limit of x as x approaches 1 for (x^2-1)/(x-1).

Line Equation

Line equation problems. For example: Find the equation of a line with points (-7,-4) and (-2,-6).

Linear Algebra

A generic problem type that can be placed with other problem types. For example: matrix and characteristic polynomial.

Linear Equation

Linear equations. For example: 4x - 3 = 2x + 9.

Linear Inequality

Linear inequalities. For example: 5x - 6 > 3x - 8.

Logarithmic Equation

Logarithmic equations. For example: log(x) = log(100).

Logarithmic Inequality

Logarithmic inequalities. For example: log(x) > log(100).

Matrix

{{1,2,5}, {3,-1,1}, {1,2,3}} row reduce

Midpoint

Midpoint problems. For example: find the midpoint between (-3, 7) and (5, -2).

Parabola

Parabola problems. For example: Find the vertex of y2 - 4x - 4y = 0.

Parallel

Parallel line problems. For example: Are the two lines parallel (y = 10x + 5, y = 20x + 10)?

Perpendicular

Perpendicular problems. For example: Are the two lines perpendicular (y = 10x + 5, y = 20x + 10)?

Polynomial Equation

Polynomial equations. For example: x^5 - 3x = 0.

Polynomial Expression

Polynomial expressions. For example: (x - 5)^4 * (x + 5)^2.

Polynomial Inequality

Polynomial inequalities. For example: x^4 - x^2 - 6 > x^3 - 3x^2.

Quadratic Equation

Quadratic equations. For example: x^2 - 3x - 4 = 0.

Quadratic Expression

Quadratic expressions. For example: x^2 - 3x - 2.

Quadratic Inequality

Quadratic inequalities. For example: x^2 - x - 6 > x^2 - 3x.

Radical Equation

Radical equations. For example: sqrt(x) - x = 0.

Radical Inequality

Radical inequalities. For example: sqrt(x) - x > 0.

Rational Equation

Rational equations. For example: 5/(x - 3) = 2/(x - 1).

Rational Expression

Rational expressions. For example: 1/(x^3 + 4x^2 + 5x + 2).

Rational Inequality

Rational inequalities. For example: 5/(x - 3) > 2/(x - 1).

Slope

Slope problems. For example: Find the slope of y = 10x + 5.

Statistics

Statistics problems. For example: Find the mean of a set of numbers (3, 8, 2, 10).

System of Equations

System of equations problems. For example: Solve 2x + 5y = 16;3x - 5y = - 1.

Trigonometry

Solve sin(t) + cos(t) = 1.

Math solver ( MathSolver ) structured data

How to add structured data

Examples

One solver action

Two solver actions

Guidelines

Technical Guidelines

Content guidelines

Structured data type definitions

MathSolver

LearningResource

Problem Type Definitions

Math solver ( `MathSolver` ) structured data