くぴんのブログ

プロフィール

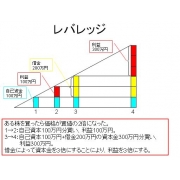
くぴん７４

フォローする

フリーページ

家電

(1)

バックナンバー

2024年11月
2024年10月
2024年09月

2024年08月
2024年07月

お気に入りブログ

DOW 44722.06 -138.2… New! どらりん0206さん

2024～25主力株概況3… New! みきまるファンドさん

楽天ラッキーくじ更…

じゃっかすさん

自分を愛することは… まりあのじいじさん
パワーアシストロボ… jhiranoさん

ニューストピックス

キーワードサーチ

▼キーワード検索

< 新しい記事

新着記事一覧(全4785件)

過去の記事 >

2011年08月15日

いまさら聞けない計算力学の常識4

カテゴリ： CAE

【送料無料】いまさら聞けない計算力学の常識
価格：3,360円（税込、送料別）

第4話　ロッキングとその逃れ方

ロッキングには2種類ある。
せん断ロッキングと体積ロッキング

○せん断ロッキング

低次要素を用いて細長い（薄い）構造物の曲げ変形を再現する際に、表現できる節点の動きが少なすぎて、”偽りの”せん断ひずみが生じてしまい、実際よりも大きなエネルギーが必要となることにより剛な応答となる現象。

○体積ロッキング

ポアソン比ν≒0.5の変形前と変形後の体積変化が非常に小さい材料（ゴムなど）のとき、体積変形以外の変形モードも生じないように拘束してしまう現象。

○ロッキングからの逃れ方

・要素内部の座標(x,y)の2次の項を含む非適合要素を使う
・次数低減積分を使う→完全積分ではなく要素中央1点の積分点で要素剛性マトリクスを計算することにより、余計な拘束を除去する。ただし、アワーグラスモードが発生する。
・選択的次数低減積分を使う→要素剛性マトリクスを体積成分と偏差成分に分解し、体積成分にのみ1点積分を適用し、偏差成分には完全積分を適用する。これにより、体積ロッキングが抑えられる。アワーグラスモードも発生しない。ただし、曲げモードによるエネルギー寄与分の一部もゼロにしてしまうので、せん断ロッキングも抑えられるが、軟らかすぎる応答が得られるので注意が必要。
・B-Bar要素を使う→上記の選択的次数低減積分は要素剛性マトリクスを体積成分と偏差成分に分解していたが、この前段階の変位-ひずみ関係を定義するBマトリクスで体積成分と偏差成分に分解し、体積成分について要素中心1点で評価する。Bマトリクスを置き換えるだけなので、プログラムへの実装が容易。Dマトリクスを体積成分と偏差成分に分解する必要もないので、違法性材料にも適用可能。非線形問題におけるな威力ベクトルの計算や接線剛性行列の計算にも利用できる。