くぴんのブログ

プロフィール

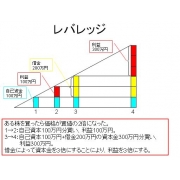
くぴん７４

フォローする

フリーページ

家電

(1)

バックナンバー

2024年11月
2024年10月
2024年09月

2024年08月
2024年07月

お気に入りブログ

DOW 44722.06 -138.2… New! どらりん0206さん

2024～25主力株概況3… New! みきまるファンドさん

楽天ラッキーくじ更…

じゃっかすさん

自分を愛することは… まりあのじいじさん
パワーアシストロボ… jhiranoさん

ニューストピックス

キーワードサーチ

▼キーワード検索

< 新しい記事

新着記事一覧(全4785件)

過去の記事 >

2015年07月11日

すでにいくつか記事を投稿しているけど、pythonの有限要素法モジュール"sfepy"についてわかったことを書いてみる。

↓sfepyの本家サイト
http://sfepy.org/doc-devel/index.html#

↓簡単な紹介pdf
http://www.ondrejcertik.com/media/euroscipy2008.pdf

http://arxiv.org/pdf/1404.6391.pdf

〇概要
sfepyはチェコ共和国のRobert Cimrmanという人が中心のグループによって開発されている。
sfepy = simple finite elements in Python
sfepyは一言でいうと、偏微分方程式を有限要素法で解くpythonモジュールである。

物理現象は場(field)を支配する偏微分方程式 (partial differential equation, P.D.E.)によって記述される。

これらの方程式は2階の偏微分方程式で、このまま(強形式のまま)解析的に厳密解を求めることが難しいことが多い。
そこで、1階の微分だけが含まれる式（1次導関数の積分の形）(弱形式)に変形する。
強形式では解に2階微分可能であることが要求されるが、弱形式では1階微分可能であればよいので、解きやすくなる。
弱形式の方程式は有限要素法によって近似解を求めることができる。

sfepyの例題をみると以下の偏微分方程式を解くことができる。

・音場(aoustics)
・拡散(diffusion)
・均質化(homogenization)
・大変形(large_deformation)
・線形静解析(linear_elasticity)
・その他(miscellaneous)

・流体(navier_stokes)
・音子(phononic)
・量子(quantum)→記述が少なくあやしい

〇使用可能な環境→Linux, Mac OS X, Windows

〇言語

コンピュータに近い、行列計算などの部分をCとFortranで記述する。
→読み書きのしやすさ(python)とスピード(C, Fortran)のいいとこどり。

〇使用可能なメッシュ
2次元の三角形と四角形、3次元の四面体と六面体、いずれも一次要素。
ビーム要素、シェル要素は今のところ対応していない。2次要素も対応していない。→残念