ラジオ、ときどきラーメン２

カレンダー

サイド自由欄

< 新しい記事

新着記事一覧(全2180件)

過去の記事 >

2015.08.15

共振周波数からＣやＬの値を求める楽な計算方法

カテゴリ：無線機

たとえば、このような共振周波数からＣの値を求める問題の場合、共振周波数の公式（ｆ＝１／（２π√（ＬＣ））から、

Ｃ＝１／（４＊π＾2＊ｆ＾2＊Ｌ）

上の例では、
Ｃ＝１／（４＊３．１４＊３．１４＊７０５０＊７０５０＊１０^6＊２＊１０^(-6)）

を計算しなければならず、計算負荷が大きくて面倒な計算になるので、計算間違いの危険性がおおきい。
それ以前に、計算が煩雑なので根性いれてやらないと計算できない。
計算が面倒でいやだ。

なので、楽に計算する方法について工夫が必要だ。

　　　　　　　　　　　　　　　　＝＞以下の様にすると、結構楽に計算できる。

まず、

すると、

１／（４＊π＾2）≒０．２５＊０．１＝０．０２５　

となる。これを最後に割り算の結果に掛ける。

上の例で計算すると、

Ｃ＝１／（４＊３．１４＊３．１４＊７０５０＊７０５０＊１０^6＊２＊１０^(-6)）
　≒０．０２５＊１／（７０５０＊７０５０＊１０^6＊２＊１０^(-6)）
　≒０．０２５＊１／（７＊７＊２＊１０^6）
　≒０．０２５＊１／（１００＊１０^6）
　＝２５０＊１０^(-12)
　＝２５０(pf)

よって、

となる。ほとんど計算の負荷がかからなくてすむ。

別の例で検証すると、

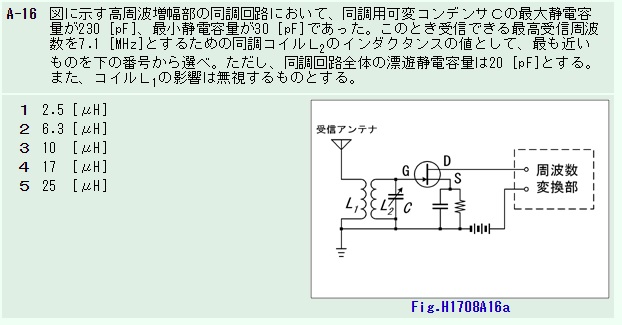
Cの可変範囲と最高周波数からLのインダクタンスを計算.jpg

（３が正解）

この問題で計算すると、
最高受信周波数とする場合、同調用可変コンデンサの値はＣ＝Ｃmin＋浮遊容量＝３０＋２０＝５０（pf）なので、

Ｌ＝１／（４＊π^2＊７．１^2＊１０^12＊５０＊１０^(-12)）
　≒０．０２５／（７^2＊５０）＝０．０２５／（４９＊５０）
　≒０．０２５／（５０＊５０）
　＝１０^(-5)
　＝１０＊１０^(-6)
　＝１０(μF)

となり、小数点の煩雑な掛け算割り算をやらなくてすむ。　

お気に入りの記事を「いいね！」で応援しよう