.　　　　　47歳今まで中途半端に生きてきたけど,この歳になって「今から医者になる」と決意しました

プロフィール

かむ太郎

フォローする

日記/記事の投稿

日本シリーズ…まずは一勝　(^へ^)v
CS突破！　(^。^)v
今年の彼岸花2025
本日の屈辱・・・(-。-)
退院してきました。
今年５回目の入院～第４日
よっしゃ！
今さら・・・星の王子さま
アクセス数・・・上位２６記事　祝(？)ブログ開設６６６６日
サピエンス全史

フリーページ

ブログリンク：秀逸なブログリンク先です。

お気に入りブログ

--< 線路沿いを行き…

New! いわどん0193さん

商談希望申込明日11… ビューティラボさん

足利大学附属女子高… ｓｅｉｋｏｔｓｕｉｎさん

ようこそ！ぶーたの… momoka1583さん
もぐらのランプ　Mol… むぐむぐもぐらさん

バックナンバー

2025年11月
2025年10月
2025年09月

2025年08月
2025年07月

カテゴリ

はじめにお読み下さい・・・Read Me 携帯用

(0)

腹膜透析の記録

(31)

キーワードサーチ

▼キーワード検索

カレンダー

< 新しい記事

新着記事一覧(全2474件)

過去の記事 >

2025年06月14日

先日の記事
「最悪！・・・上等上等(*へ*)」

で、「微分・積分」のお世話になる。

との記載をしましたが、

そこのところをしっかりと説明してなかったので

補足（蛇足とも言う）を少々。

「極小値」と「極大値」を、それぞれ人生のその時点での

「一見最悪（極悪と名付く）」「一見絶頂」とし、

その時々の状況を「良き」「悪しき」としましたが、

高校数学（特に共通テストの出題範囲）で学ぶ「微分・積分」では

・３次関数のグラフに引いた接線
・極大値・極小値
・グラフと接線で囲まれた部分の面積

などが問われます。

ここで、重要なのは、

「極大値」「極小値」での接線の傾きは「０（ゼロ）」

ということです。

即ち、

「極小値」に至るまでは

その前から、す～っと「人生転がり続けて」グラフの傾きは

「極小値」になった瞬間
　※実は現実の人生では、この瞬間はまだ極小値だとはわからない。
　　この後少しでもグラフが上向き（傾きがプラス）になって
　　はじめて、「あ、あの時点が極小値か。」と判明するのです。
　　ま、それにすら気づかないのが実情なんですが・・・

ではあるのですが、極小値を超えた時点で

グラフは着実に上向きなのです。

ただ、これに気づかないと、

置かれている状況（ｙ軸の値）自体は「マイナス」なので

せっかくグラフが上向いて（その時々の接線の傾きもプラス）

いるのに意気消沈の日々を送ってしまい

せっかく呼び込んだ「順風」にも気づけず

みすみす運気を逃してしまいます。

今の状況が「見かけ（ｙ軸上）の値はマイナス」でも

グラフの傾き（そこに引いた接線の傾き）は

しっかりと「プラス」になっているのです。

$増減表の作り方4_変曲点の求め方$

上のグラフは

ｆ(x)=２x^３－６x
　　（注）x^３は「xの３乗」の意。

ですが、これを人生に見立てると（ｘ軸左から右へ時間推移）

（１，－４）の時点はここで見る限り

ここ最近（ｘがー２あたりから最近まで）で「人生最悪」であり

実際の人生になぞらえると

左の方の「無限に下がる（＝時間軸の即せば、無限のマイナスからの上昇）」

は有り得ないので、実際の人生は「ｘ＝－２（y軸の値が０）」あたりから開始。

つまり、グラフの定義域を「－２≦ｘ」とすると

さきほどの（１，－４）の時点は「極小値＝ここ数年で最悪」でもあり

結果、それまでの人生（定義域内）の「最小値＝過去の人生最悪」でもある。

このあたりの理屈は、前の日記参照。

問題は、この「極小値＝一見最悪」と思われる時点が

冷静に「グラフに接する接線の傾き」を見定めると

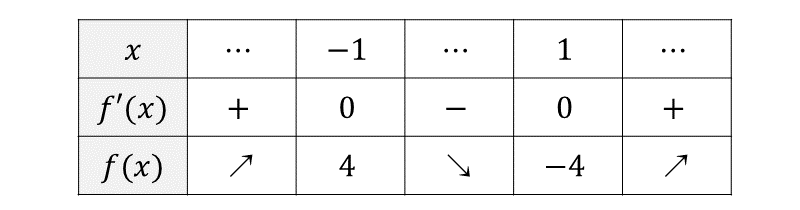
$三次関数の増減表$

これは、「数学Ⅱ」で頻繁に目にする「増減表」です。

与えられた式「ｆ(x)=２x^３－６x」を微分する（表の２段目）と

f’(x)=６x^２-６となります。

f’(x)=０を解くと、x=±１

f’(x)＝０　即ち「極大値」「極小値」のｘの値が出ます。

この時点こそが、「グラフの傾き：ｆ’(x)」が

「マイナスからプラス」

「プラスからマイナス」

の転じる分岐点なのです。

ですから、ｆ(x)・・・これは見かけの現状（グラフのｙ軸の値）

が「－４」で人生最悪に見えても、

この時点を過ぎれば、ｆ’(x)・・・グラフの傾向（接線の傾き）は「+」

しっかりと矢印が上を向いているのです。

逆も然り・・・で、

絶頂期・・・だった「ｘ＝－１」からしばらくは、「y軸」の値が「+」

で、見かけの状況は「+」ではあるのですが、

実は、グラフの傾きは「－」で、その後奈落の底へ向かっていたのです。

否！「ｘ＝－１（絶頂期）」の直後から既に奈落の底まっしぐら・・・だった。

この時も、冷静に

ｆ’(x)の値が「ｘ＝－１」の絶頂期以降は「－」であり

矢印も「下向き」との警告が出ていたのです。

上のグラフを見ていれば

この理屈は言うまでもなく理解できることと思われますが

実際の人生では、このようなグラフは目に見えないし

かつ、グラフのように「全体像」も「この先」も見えません。

従って、

「今」がどんな状態なのか、をしっかりと把握することが

何よりも大切なことではないか、と感じております。

この一連の考え方は、私の座右の銘である

「人間万事塞翁が馬」にも通ずるものがると思えます。

理想は、

y軸の値＝見かけの現状が「良き！」

かつ、ｆ’(x)の値も「+」＝接線の傾きが「+」

が続くことですが、

なかなかそうも参りません。

せめて、「極悪」の状況でも、「ｆ(x)」だけを見るのではなく

一回微分してみて、冷静に「ｆ’(x)」の値を見極めるだけの

余裕を持って生きていきたいものです。

※「積分」は、どないなってんね！

という苦情が想定されますが、

今回は、「訴状が届いていないのでコメントできない。」

・・・というコメントの後に

「やっと訴状が届きましたので・・・」

と言って記者会見するっていうのは聞いたことないね。

結局、訴状はどこにも届かないまま・・・なのか？

お気に入りの記事を「いいね！」で応援しよう