★いきいき健康・ゆとり生活・応援団！

■エージロー先生の受験生応援特別講座【1】

【１】 【２】 【３】 【４】 【５】

エージロー先生の受験生応援特別講座【1】

■ 中学校数学学習サイト 　数学の勉強法。数学は考える教科です。

ある問題で特殊なテクニックを使えば普通より短時間で解ける場合があります。 そしてそういった方法を沢山暗記していくことが数学

の受験勉強だとする学習塾や 参考書も少なくありません。

ところが、やり方を暗記することによって数学でもっとも 必要な「柔軟な思考」をうばってしまうことになります。……（以下略）

■ 無料で使える中学学習プリント（数学）

■ 中学・学習サイト～勉強法と練習問題～ これは自塾の練習問題として作成し‥‥（以下略）

■ 中学校数学学習サイト 　直角三角形の合同条件など。

■ オール５家庭教師の学習法

■ 金曜ドラマ『下剋上受験』HP by TBSテレビ　 (2017.02.10.Fri.)

■ iPadスタイル

中1・高1・高2タブレット学習。

≪Ｚ会の通信教育≫今すぐ無料体験！ より深く楽しく学ぶ。新しい学習スタイル。

■ 最高の解答へ、ようこそ。高校生・大学受験生 Ｚ会の通信教育

一人ひとりに応じた的確な添削指導で 難関大合格に直結する「考えて書く力」を育てます。

■ 進研ゼミ小学講座 by Benesse

■実は、私エージローも大阪で高校生活を送っていたとき、教育熱心だった父母の勧めで旺文社の数学の添削指導を受けていましたが、

その後、社会人となって、大阪道修町の創業300年の製薬会社（東証一部）開発部門から出版社（進学塾併設）に移ったとき、編集部で

教育図書（単行本）や、小学生向けや高校受験用の学習参考書、副教材、5教科の本格的な問題集などを編集したり、英語の問題作成委

員や大阪府の模試の出題チェッカーを担当したりしていました。

最近では、全国に少数精鋭の500人しか居ないというハードな指導陣の一人に抜擢されて、Z会の高校2年の数学(M2S)の通信添削指導

員を8年間にわたって担当し、定年後の現在、小1～中3生～(高卒生)の家庭教師（岡山市内の教材会社と連携する個人事業）や塾講師

（小1～高3生）を続けていますが、悩みの種は英語と数学、特に数学の成績が悪く、苦手意識が強くて伸び悩んでいる生徒さんがとて

も多いことです。

そこで今回、高校受験を控えた会員の皆さんたちの最も苦手とする数学の応用問題、証明問題、図形問題（※注）、文章題、総合問題

などについて、難問を易問に変えてしまうようなオリジナルで画期的な解法を開発しましたので、ここに公開していくことにしました。

受験生の皆さんの数学の成績アップに是非お役立てください。

（※注）高校入試の数学において、図形問題の出題率は全体の約39%とされています（旺文社の全国高校入試問題正解数学2015）。

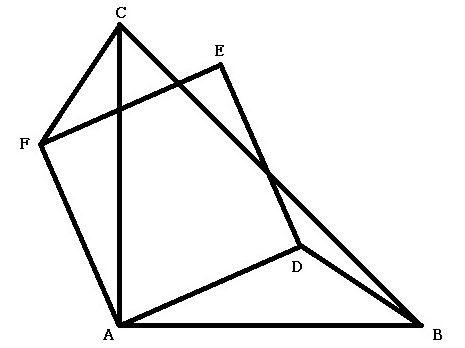
【問題１】右の図で、四角形ABCDと四角形AEFGはともに正方形であり、点Eは辺BCの延長上にある。

△ABE≡△ADGであることを証明しなさい。 （26岐阜）　（配点 16点）　
  • 【Ｒ】15-08-29-6数学・三角形の合同（２６岐阜）.jpg

【解説】n角形の内角の和＝(n-2)×180° ⇒四角形ならば (4-2)×180°=360°

（注）多角形の外角の和=360°（常に一定）

【証明】△ABEと△ADGにおいて、四角形ABCDは正方形だから、AB=AD ‥‥‥‥‥‥‥‥‥‥‥‥(1)

また、四角形AEFGは正方形だから、　　　　　　　　 　 　 　　AE=AG ‥‥‥‥‥‥‥‥(2)

ここで、三角形の合同条件「2組の辺とその間の角がそれぞれ等しい」

を満たすには、(1)と(2)および、　　　　　　　　　　 　∠BAE=∠DAG ‥‥‥‥‥‥‥‥(3)

であればよいから、∠BAE=x、∠DAG=yとするとき、x=yが示せればよい。

ここで、AEとCDの交点をHとするとき、四角形EFGHにおいて、

∠F=∠HEF=90°（∵四角形AEFGは正方形）、

∠HGF=∠AGF-∠AGD=90°-(90°-y)=y、

∠EHG=180°-x（∵AB∥HCより∠CHE=x）だから、「四角形の内角の和=360°」より、

90°＋90°＋y＋(180°-x)=360° ‥‥‥‥‥‥‥‥‥‥‥‥(4)

ゆえに、(4)よりx=yが導き出されて (3)が成り立つので、

(1)、(2)、(3)より　△ABE≡△ADG 　（証明終わり）　　　　　 　　　　　

(2015.08.29.Sat.作成)

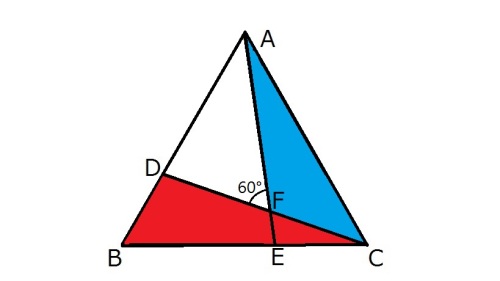
【問題２】右の図において、三角形ABCは正三角形で、辺AB、BC上にそれぞれ点D、Eをとり、AEとCDの交点をFとする。

∠AFD=60°のとき、AE=CDとなることを証明しなさい。 （25福島）
  • 【R】15-09-27-8三角形の合同問題4.jpg

【解説】

AEとCDをそれぞれ辺に持つ2つの三角形△AECと△CDBが合同であれば、AE=CDが言えます。

△AECと△CDBにおいて、AC=CB、∠ACE=∠CBD（=60°）だから、あと1つ、

∠CAE=∠BCDが言えれば、三角形の合同条件「１組の辺とその両端の角がそれぞれ等しい」が使えます。

△AFCに着目すると、∠CAE=60°-∠ACF、

∠ACB=60°に着目すると、∠BCD=60°-∠ACFとなります。　

【証明】

問題の「∠AFD=60°のとき、AE=CDとなることを証明する」には、　

「∠AFD=60°のとき、△AEC≡△CDBとなることを証明」すればよい。 　

△AECと△CDBにおいて、AC=CB　　‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥　(1) （∵△ABCは正三角形）　

∠ACE=∠CBD（=60°）　　‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥　(2) （∵△ABCは正三角形）　

だから、あと1つ、∠CAE=∠BCD　　 ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥　(3)

が示せれば、三角形の合同条件「１組の辺(1)とその両端の角(2)(3)がそれぞれ等しい」が満たされて、

「∠AFD=60°のとき、△AEC≡△CDBとなり、AE=CDとなる」ことが証明される。

ここで、(3)の∠CAE=x、∠BCD=yとするとき、x=yが示せれば(3)が成り立つから、

△AFCにおいて、

∠AFC=180°-∠AFD=180°-60°=120°

∠ACF=60°-∠BCD=60°-y

だから、三角形の内角の和=180°より、

120°+x+(60°-y)=180°　‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥　(4)

ゆえに、(4)よりx=yが導き出されて、(3)が成り立つので、

(1)、(2)、(3)より、∠AFD=60°のとき、AE=CDとなる。（証明終わり）

(2015.09.28.Mon.作成)

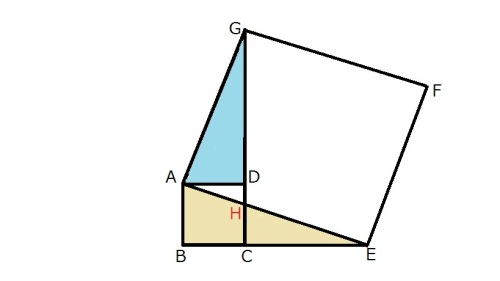
【問題３】下の図のように、1つの平面上に∠BAC=90°の直角二等辺三角形ABCと正方形ADEFがあります。

ただし、∠BADは鋭角とします。このとき、△ABD≡△ACFであることを証明しなさい。（27広島）（配点4点 / 50点満点）
  • 【Ｒ】15-11-30-9広島県数学合同問題.jpg

【解説】

「∠FAD=∠CAB=90°だから、点Aを中心に辺AFを時計回りにy°だけ回転させると、

辺AF、ADはそれぞれ辺AC、ABに重なるから、x=yである。」

という考え方もあり、これはいろいろな問題を解くときに応用できます。

【証明】

△ABDと△ACFにおいて、

△ABCは直角二等辺三角形だから、AB=AC ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥(1)

四角形ADEFは正方形だから、AD=AF 　　 ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥(2)

だから、あと一つ、∠BAD=x、∠CAF=yとおくとき、x=yが示せれば、

三角形の合同条件「二組の辺(1)(2)とその間の角(3)がそれぞれ等しい」を満たすことになる。

ここで、△OABは直角三角形だから、∠CAB=90°

したがって、∠CAD=∠CAB－∠DAB=90°-x

また、四角形ADEFは正方形だから、∠FAD=90°

ゆえに、∠FAD=∠FAC＋∠CADより、

90°＝y＋(90°－x)

これより、x=yだから、∠BAD=∠CAF　　　‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥(3)

ゆえに、(1)・(2)・(3)より、△ABD≡△ACF　　　（証明終わり）

(2015.11.02.Mon.作成)

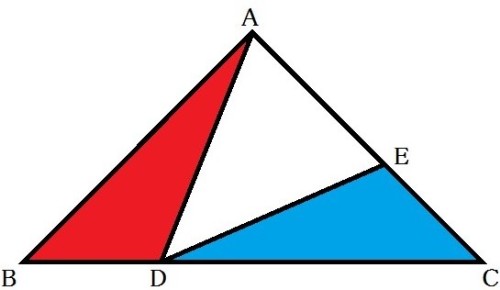
【問題４】右の図で、△ABCはAB=ACの二等辺三角形、Dは辺BC上の点で、∠ADC=∠DAC、Eは辺AC上の点で、∠BAD=∠CDEであ

る。次の問いに答えなさい。

（１）△ABDと△DCEが合同であることを証明しなさい。

（２）∠ABD=50°のとき、∠BADの大きさを求めなさい。

（３）△ABCの周の長さが26cmで、△ABDの面積が△ABCの面積の1/5倍のとき、辺ABの長さを求めなさい。 （27広島県模試）
  • 【Ｒ】15-12-02-9第4回実力模試数学大問５.jpg

【解説】（３）については、求める辺AB(=DC)の長さをycmとすると、AB＋BC＋CA=2y＋BC=26cmより、BC=(26-2y)cm、

BD=BC-DC=(26-2y)-y=(26-3y)cm

△ABDと△ABCは、底辺をそれぞれBD、BCとする高さが同じ三角形だから、その面積の比は底辺の長さの比となるので、

題意より、BD:BC=1:5=(26-3y):(26-2y)　とすればよい。

【解答】（１）△ABDと△DCEにおいて、

∠ADC=∠DACより△CADは二等辺三角形だから、AC=DC(=AB)

また、△ABCは二等辺三角形だから、題意より、AB=AC(=DC)

ゆえに、 AB=DC 　　 　‥‥‥‥‥‥(1)

また、題意より、∠BAD=∠CDE ‥‥‥‥‥‥(2)

さらに、△ABCは二等辺三角形だから、題意より、∠ABD=∠DCE ‥‥‥‥‥‥(3)

したがって、(1)・(2)・(3)より、

「一組の辺(1)とその両端の角(2)(3)がそれぞれ等しい」（三角形の合同条件）から、△ABD≡△DCE　　（証明終わり）

（２）求める∠BAD=xとおくと、2∠DAC=2∠ADC=180°-50°=130°　

ゆえに、∠DAC=∠ADC=65°

ゆえに、x=∠BAC-∠DAC=(180°-50°×2)-65°=80°-65°=15°

（答）15°

（３）求める辺AB(=DC)の長さをycmとすると、

AB＋BC＋CA=2y＋BC=26cmより、BC=(26-2y)cm

△ABDと△ABCは、底辺をそれぞれBD、BCとする高さが同じ三角形だから、その面積の比は底辺の長さの比となるので、

題意より、BD:BC=1:5

したがって、CD:CB=4:5=y:(26-2y)

ゆえに、5y=4(26-2y) より y=8

（答）8cm

(2015.12.02.Wed.作成)

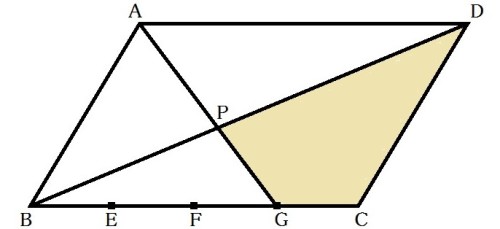
【問題５】次の図のように、平行四辺形ABCDの辺BCを４等分する点をE、F、Gとし、AGとBDの交点をPとします。
  • 【Ｒ】15-12-04-7数学図形問題良問１.jpg

これについて、次の（１）、（２）に答えなさい。

（１）△ABPと△BGPの面積の比を、最も簡単な整数の比で表しなさい。

（２）△ABCの面積が56㎠のとき、四角形CDPGの面積を求めなさい。　（広島県内・公立中学・受験生用練習問題プリント）

【解説】中学3年生の生徒さん（受験生）から質問があったもので、これは「相似」や「相似比」を利用する問題でもあり、平行四辺形

の性質をうまく応用した、面積だけが等しい、いわゆる「等積」の三角形を利用する図形問題、よく出題される重要な問題です。

【解答】（１）△ABPと△BCPは等積（面積が等しい）だから、面積について、

△ABP:△BGP=△BCP:△BGP

ここで、△BEP=△EFP=△FGP=△GCP（等積）だから、

△ABP:△BGP=△BCP:△BGP=4△GCP:3△GCP=4:3

（答）４：３

【補足】△ABPと△BGPは、それぞれ辺AP、GPを底辺とする 高さが同じ三角形であると考えると、その面積比はAP:GPである。

ここで、仮定よりDA//BGだから、3組の角（錯角と対頂角）がそれぞれ等しいことより、△DAP∽△BGPであり、

その相似比＝DA（＝BC）：BG＝４：３＝AP:GP＝△ABP：△BGP（＝面積比）　

ゆえに、求める面積の比は、△ABP：△BGP＝４：３ 【2017.12.29.Fri.更新】

（２）△ABC=△BCD=56㎠（等積）だから、

求める四角形CDPGの面積S=△BCD-△BGP 　　　　　　　　 ‥‥‥‥(1)

△ABPの面積=x㎠、△BGPの面積=y㎠とすると、（１）より、x:y=4:3

ゆえに、　　　　　　　　　　　　　　　　　　3x=4y ‥‥‥‥(2)

また、面積について、△ABC=4△GCA=56 より、△GCA=56/4=14㎠

ゆえに、△ABCについて、56=x+y+14 より、x+y=42 　　 ‥‥‥‥(3)

したがって、未知数x、yについての連立方程式(2)・(3)を解くと、x=24、y=18

ゆえに、(1)より、求める面積S=△BCD(=△ABC)-△BGP=56-y=38

（答）38㎠

(2015.12.04.Fri.作成)

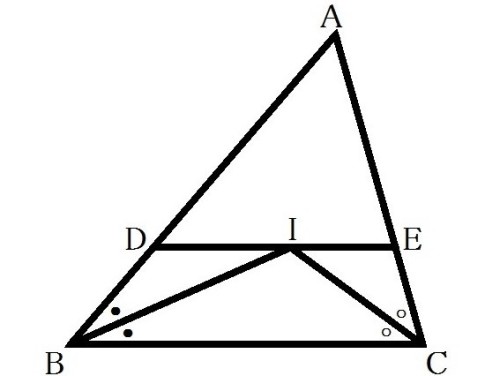
【問題６】右の図の△ABCにおいて、∠Bと∠Cの二等分線の交点をIとする。また、点Iを通り、辺BCに平行な直線と辺AB、ACとの交点

をそれぞれD、Eとする。このとき、次の問いに答えなさい。
  • 【Ｒ】15-12-13-6如水館27数学入試問題.jpg

（１）∠A=52°のとき、∠BICの大きさを求めなさい。

（２）AB=10cm、BC=8cm、∠CAB=∠CBAのとき、△ADEの3つの辺の長さの和を求めなさい。（27広島県内）

【解説】相似な二つの三角形を使った重要問題で、（２）のポイントは、線分DE=DI+IE=(10-y)+(8-z)=z というふうに、線分DEを

二つの違った方法で表す技法です。

【解答】（１）∠A=a、∠B=b、∠C=c、求める∠BIC=xとおくと、

a=52°、△ABCまたは△ADEにおいて、a+b+c=180°より　52°+(b+c)=180°だから、

b+c=128°　‥‥‥‥‥‥‥‥‥‥‥‥(1)

また、△BICにおいて、b/2+c/2+x=180°より、2x=360°-(b+c) ‥‥‥‥‥‥‥‥‥‥‥‥(2)

ゆえに、(1)・(2)よりx=180°-64°=116°

（答）116°

（２）AD=ycm、AE=zcmとおくと、∠A=∠Bより、△ABCはAC=BCの二等辺三角形だから、

AC=BC=8cm

また、DE//BCより、△ABC∽△ADEだから、AE=DE=zcm

求める△ADEの3辺の長さの和L=AD+DE+EA=y+2z ‥‥‥‥‥‥‥‥‥‥‥‥(3)

また、DI=BCより、∠DBI=∠CBI=∠DIBだから、△DBIはDB=DIの二等辺三角形であり、

したがって、DB=DI=AB-AD=(10-y)cm

同様に、△ECIはEC=EIの二等辺三角形だから、EC=EI=AC-AE=(8-z)cm

ゆえに、線分DE(=z)=DI+EI=(10-y)+(8-z)

したがって、z=(10-y)+(8-z)より、y+2z=18 ‥‥‥‥‥‥‥‥‥‥‥‥(4)

ゆえに、(3)・(4)より、L=y+2z=18

（答）18cm

なお、相似な二つの△ABC、△ADEより、y:10=z:8だから、5z=4y 　 ‥‥‥‥‥‥‥‥‥‥‥‥(5)

ゆえに、(4)・(5)より、y=90/13 cm、 z=72/13 cm

(2015.12.13.Sun.作成)


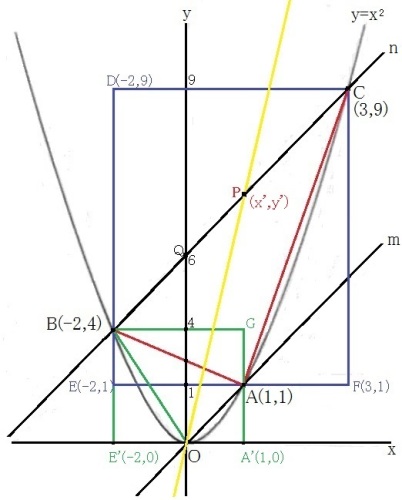
【問題７】右の図で、曲線は関数y=x²のグラフである。原点Oと点Aを通る直線をmとし、点Bを通り、mに平行な直線がy=x²のグラフ

と再び交わる点をCとする。このとき、次の問いに答えなさい。
  • DSCN9445-7放物線図形問題因島池田君.jpg

（１）△ABCの面積を求めよ。

（２）原点Oを通り、四角形OACBの面積を二等分する直線の式を求めよ。

【解説】この問題は全国的に毎年よく似た類似問題が頻繁に出題されるようなおなじみの重要問題ですが、基本的なポイントを抑えて

しっかりと理解しておくことが大切です。

（２）のポイントは △OPQの面積=△OBPの面積-△OBQの面積=9-6=3=6×{6/(k-1)}×1/2 です。

【解答】（１）y=x² ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥(1)

直線mは原点Oと点A(1,1)を通るので、傾き1の直線だから、

m：y=x ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥(2)

点Cは、(1)上の点B(-2,4)を通って(1)と再び交わる点で、線分BCは傾き1、y切片6の直線だから、これを直線nとすると、

n：y=x+6 ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥(3)

また、(1)と(3)の交点Cの座標は、y=x²=x+6より、x²-x-6=0

ゆえに、(x+2)(x-3)=0 より　x=-2,3だから、点C(3,9)

点D(-2,9)、点E(-2,1)、点F(3,1)とすると、長方形CDEFの面積S=8×5=40

ここで、△BCDの面積a=5×5×1/2=25/2

△ABEの面積b=3×3×1/2=9/2

△ACFの面積c=2×8×1/2=8

ゆえに、これらの和=a+b+c=25

したがって、求める△ABCの面積=S-(a+b+c)=40-25=15

（答）15

（２）点A'(1,0)、点E'(-2,0)、点G(1,4)、点P(x',y')、点Q(0,6)とすると、

長方形A'GBE'の面積S'=4×3=12

ここで、△OE'Bの面積d=2×4×1/2=4

△OA'Aの面積e=1×1×1/2=1/2

△AGBの面積f=3×3×1/2=9/2

ゆえに、これらの和=d+e+f=9

したがって、△OABの面積=S'-(d+e+f)=12-9=3

ここで、四角形OACBの面積=△ABCの面積+△OABの面積=15+3=18

ゆえに、二等分された△OBPの面積=18×1/2=9

また、△OBQの面積=6×2×1/2=6

ここで、求める直線の式：y=kx ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥(4)

とおくと、(4)と直線n:(3)との交点P(x',y')のx座標は、

y=kx=x+6 より (k-1)x=6

ゆえに、x'=6/(k-1)、また、P{6/(k-1),6k/(k-1)}

したがって、△OPQの面積=△OBPの面積-△OBQの面積=9-6=3=6×{6/(k-1)}×1/2

ゆえに、3(k-1)=18 より、k=7

したがって、(4)より、求める直線の式はy=7x

（答）y=7x

(2015.12.15.Tue.作成)

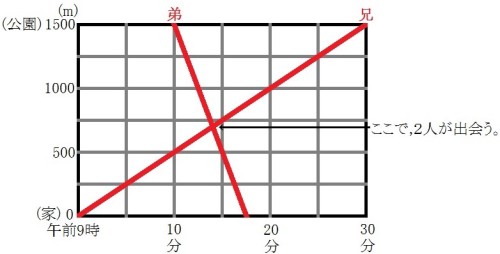
【問題８】下の図の横軸は時刻を、縦軸は家から公園までの道のりを示しています。午前9時に兄は家に、弟は公園にいて、同じ道を次

のように移動しました。これについて、あとの問いに答えなさい。

［兄］ 午前9時に家を出て、毎分50mの速さで公園まで歩いて行った。

［弟］ 午前9時10分に公園を出て、毎分200mの速さの自転車で家に帰った。
  • 【Ｒ】15-12-16-7連立方程式の応用問題１.jpg

（１）兄と弟の移動の様子を表すグラフをかけ。

（２）兄と弟が出会った時刻を求めよ。

【解説】

これは、中学3年の生徒さん（受験生）から質問を受けた連立方程式の応用問題の一つです。

（１）兄は10分間に500m歩き、弟は5分間に1000m進むことからグラフをかけばよい。

（２）9時x分のときの家からの道のりをymとして直線の式を求めると、兄はy=50x、弟はy=-200x+3500であり、この2つを組み合

わせてできる連立方程式を解くと、x=14

グラフからは出会う時刻が読み取れないので、直線の式を組み合わせた連立方程式を解いて求める。

【解答】

（１）[兄]は午前9:00に徒歩（50m/分）で家から公園に向かい、

[弟]は午前9:10に自転車（200m/分）で同じ道を公園から家に向かうので、

二人が [家 ⇌ 公園] の1500mの道のりを行くのに、[兄]はx分、[弟]はy分かかったとすると、

[兄]（徒歩）　　50:1=1500:x　ゆえに、50x=1×1500　

したがって、x=30（分）　　　　　‥‥‥‥‥‥‥‥‥‥‥‥[兄]の「家から公園まで」の所要時間　

[弟]（自転車）　200:1=1500:y　ゆえに、200y=1×1500　

したがって、y=7.5（分）　　　　　‥‥‥‥‥‥‥‥‥‥‥‥[弟]の「公園から家まで」の所要時間　

ゆえに、[兄]は２点（0, 0）、（30, 1500）を通る直線となり、その直線の式は、

x:y＝(30−0):(1500−0)より、30y=1500x　　

ゆえに、y=50x　　‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥(1)　：[兄] の移動の様子を表すグラフ

また、[弟]は２点（10, 1500）、（17.5, 0）を通る直線となり、その直線の式を

y=ax＋b　　‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥(2)

とおくと、２点（10, 1500）、（17.5, 0）は直線(2)上の点だから、

1500=10a+b　　 ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥(3)

0=17.5a+b 　 ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥(4)

ゆえに、(3)−(4)より、1500=−7.5a ゆえに、a=−200

したがって、(4)より、b=−17.5a=−17.5×(−200)=3500 ゆえに、b=3500

したがって、(2)は　y=−200x+3500 ‥‥‥‥(5)　：[弟] の移動の様子を表すグラフ　

ここで、(1)と(5)の連立方程式を解く（解を求める）、つまり、直線(1)と直線(5)の交点Ｐの座標(x, y)を求めると、

(1)の右辺=(5)の右辺 だから、50x=−200x+3500 　ゆえに、250x=3500

ゆえに、x=14（分）

さらに、(1)より、y=50x=50×14=700 ゆえに、y=700(m)

したがって、直線(1)と直線(5)の交点Ｐの座標は (14, 700)

ゆえに、

（２）兄と弟が出会った時刻は　午前9時14分　‥‥‥‥‥‥‥‥‥‥（答）

(2015.12.16.Wed.作成)

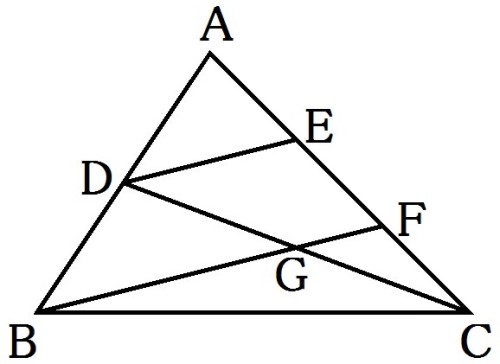
【問題９】右の図の △ABCで、AD=DB、AE=EF=FCである。また、線分 BF、DC の交点を G とする。

BF=10cm のとき、BG の長さを求めなさい。（27国立高専・国立工業高専・国立商船高専）（5点/100満点）
  • 【Ｒ】15-12-18-6国立高専27数学（相似）入試問題.jpg

【解説】

「中点連結の定理」を使って、△ADE∽△ABF、△CFG∽△CED、DE//BF、GF//DEより、

CF:CE=CG:CD=FG:ED=1:2=(10-x):5を導けばよい。

【解答】

求めるBGの長さをxcmとすると、「中点連結の定理」より △ADE∽△ABF であり、

したがって、AD:AB=AE:AF=DE:BF=1:2 で、また、DE//BF であるから、BF=10cmより

DE=5cm、また、GF=BF-BG=(10-x)cm

さらに、DE//GFより、△CFG∽△CEDだから、

CF:CE=CG:CD=FG:ED=1:2=(10-x):5

ゆえに、2(10-x)=5より、x=7.5cm

（答）7.5cm

(2015.12.18.Fri.作成)


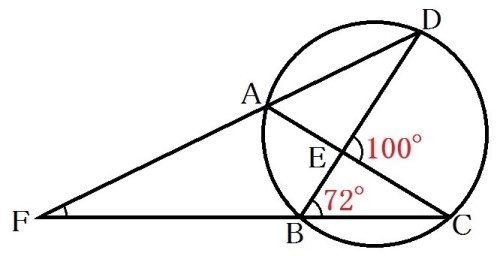
【問題１０】右の図のように、円周上に4点A、B、C、Dがあり、ACとBDの交点をE、DAとCBが延長線上で交わる点をFとします。

∠DEC=100°、∠EBC=72°のとき、∠AFBの大きさは何度ですか。
  • 【Ｒ】15-12-19-6数学円周角問題１.jpg

【解説】

同じ長さの円弧に対するものであれば、その円周角はすべて常に等しいことを利用します。

以下を使ってもよい。

n角形の内角の和＝(n-2)×180° ⇒ 三角形ならば(3-2)×180°=180°、

四角形ならば(4-2)×180°=360°、五角形ならば(5-2)×180°=540° ⇒ 正五角形ならば、一つの内角=540°/5=108°

（注）多角形の外角の和=360°（常に一定）

つまり、四角形FAEBを考えると、∠F=(4-2)×180°-(100°+108°×2)=360°-316°

【解答】

円周角∠CBD=∠CAD=72°、円周角∠ADB=∠ACB=100°-72°=28°、

∠FBD=∠FAD=180°-72°=108°だから、△FACまたは△FBDについて考えると、

求める∠AFB=180°-(108°+28°)=44°

（答）44°

(2015.12.19.Sat.作成)

　　‥‥‥【文責・写真】エージロー（２０１７．０７．２５．Ｔｕｅ．更新）
‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥

■ 成績アップの、新常識。勉強サプリ 夢中になれる授業がいっぱい！　by リクルート

リクルートの勉強サプリ：一流講師の授業動画が980円（税抜）！飽きずにつづくオンライン学習。

■ 朝日学生新聞社｜ジュニア朝日

■ 学校向けICT教材「すらら」【公式】

■ オール５家庭教師の学習法 高校受験で不合格になる子の特徴。

秋から成績が伸び悩むと危険？ 塾や家庭教師で頑張って勉強しても不合格になる理由。

■ 渋柿を焼酎で渋抜きする方法とは！？柿を甘くするたった３つの手順 　by ためになる雑学が５分で学べるブログ

■ 血液はないのに…1割の植物に「人間と同じく」血液型がある理由 　2015.07.12 -by Suzie

普段気付かない意外な発見と驚きの数字が満載！　

日本人は血液型トークが好きですよね。よく「◯◯さんはO型だから～」なんて話をします。

でも、この血液型、人間だけのものではありません。

動物にも血液型があって、魚はA型、亀はみんなB型、チンパンジーは人間と同じA・B・O・AB型があるという話は有名ですよね。

でも、植物にも血液型があることをご存知でしょうか？　‥‥（以下略）

■ 受験生の子どもがいるあなたへ

■ この冬、チャレンジタッチを始めるチャンス 　by Benesse 進研ゼミ

小学生のタブレット学習教材「チャレンジタッチ」のここがすごい。

問題は授業形式で展開 即時の正誤判定で根本から正しく理解。

■ レンタルフォント

■ チャレンジタッチ by Benesse
「チャレンジタッチ」は、夢中で学べるのはもちろん、学習効果も証明されています。

■ 受験サプリ

受験サプリとは、勉強を頑張るすべての受験生を応援するサービスです。

圧倒的にわかりやすい講義動画が月額980円(税抜)で見放題！

■ TVアニメ「暗殺教室」公式サイト

■ TOEIC満点＆アメリカ移住ブログ

■ 血管をしなやかにする「年齢ペプチド」とは？ 　by 「カルピス」由来健康情報室　(2016.05.10.Tue.)

■ 【超厳選】おすすめの英文法参考書10選

年間200万人以上が見る大学受験勉強法メディア「奇跡の勉強法」(2016.12.07.Wed.)

■ 数学のたまご （中学1～3年生向け）　(2016.12.07.Wed.)

■ 二項定理 （高校数学） 　in Wikipedia (2016.12.18.Sun.)　

■ 6年算数 規則性に関する問題 　　(2016.12.25.Sun.)　

■ 高校生の苦手解決Q&A 数学【場合の数と確率】 Presented By 進研ゼミ＋高校講座

あなたの苦手を進研ゼミプラス高校講座が解決します！　(2017.01.09.Mon.)　

■ スタディサプリ（大学受験講座）高1スタンダードレベル数学IA IIB＜集合＞ 　(2017.01.09.Mon.)　

■ 「もうややこしくない！自動詞と他動詞の見分け方」など 　by 英語魂　(2017.01.09.Mon.)　

■ 無料で使える中学学習プリント（数学） 　(2017.01.20.Fri.)　

■ 「脳の老化」と「栄養」の関係を、テレビで人気の古賀先生が解説！ by サントリー 　(2017.01.29.Sun.)　

あれ？人の名前が出てこない‥‥、それ、「脳」の老化のサインかも！？

■ 50万人の中高生に読まれる学習メディアQikeru 　by QIKERU 　

確率 | QIKERU：中学生のための無料学習サイト (2017.02.04.Sat.)　

■ ナビ個別指導学院 三原校 　あなたの町の個別指導塾・学習塾です。　0120-941-967 (2017.02.10.Fri.)

私エージローが、塾講師として勤務する広島県・JR三原駅前の三原校です。小学1年～高校3年まで、塾生の皆さんも苦手科目の克服を

目指して毎日、しっかりと頑張っています。（エージロー先生紹介でＨＰに詳細を掲載中）

■ 金曜ドラマ『下剋上受験』HP by TBSテレビ　 (2017.02.10.Fri.)

■ 2017年 広島県公立高校入試 解答速報 　2017年3月7日（火）/ 8日（水）午後3:00～3:50　by つながる HOME 5CH　

(2017.03.06.Mon.)

■ 新・働き方 総合研究所 　(2017.03.20.Mon.)

■ Toshin.com 予備校・大学受験の東進ドットコム 　(2017.03.21.Tue.)

■ 3人のうち少なくとも2人の誕生月が同じである確率を求めよ。

生徒さんより質問のあった問題（類似問題）です。(2017.03.25.Sat.)

■ ソニーの語学学習モデル商品ガイド 　(2017.03.25.Sat.)

■（参考） 「灘→東大理Ⅲ」の3兄弟を育てた母の秀才の育て方 佐藤亮子 著

私エージローは以前に８年間、Ｚ会（Z-kai）の高２数学Ｍ２Ｓ標準コースの通信添削指導員をしていましたが、その会員のほとんどが

灘、開成、ラサールなど、全国の有名進学高校の生徒さんたちで、希望する進学先は大学受験の最難関・最高峰の東大理Ⅲ（医）でした

から、全国に５００人しか居なかった私たち数学の指導員のその対応ぶりも締め切りに追われながら寸暇を惜しんでの熱気あふれるもの

となり、パターン別の力がつく最強の合格答案の作り方について、「答案に直」の赤ペンで一生懸命に細かく書き込みを入れ「通信

欄」、「質問箱」も用意するなど、徹底した指導（累計で延べ約８,０００枚の合格答案の指導）を行っていたのでした。

‥‥（つづく）　(2017.03.28.Tue.)


▲息子3人に続き娘も東大理Ⅲ（医）に合格！佐藤亮子・受験のプロママが生激白！(2017.04.06.Thu.)

■ ありがとう20周年！家庭教師のデスクスタイル

電話やFAXで添削指導など万全サポート。指導料１時間１,５００円、生徒１人に講師２名。　(2017.04.16.Sun.)

■ 接弦定理の証明 　　(2017.05.18.Thu.)

■ 無料で使える中学学習プリント（接弦定理）

接線と弦の作る角の定理を用いた問題です。基本事項を理解してから、角度を求める問題や証明問題を解きます。いろいろな問題を解い

て、慣れるようにしてください。 (2017.05.18.Thu.)

■ 現役東大生二人が教える「どうして東大を目指し、どのように合格したのか」現役東大生対談！【西岡壱誠×綱島将人】

by ダイヤモンド社のビジネス情報サイト 書籍オンライン　 (2017.05.26.Fri.)

■ 猫でもわかる秘密の英語勉強会 　　 (2017.07.22.Sat.)

■ DMM英会話 鬼に金棒って英語でなんて言うの？　　(2017.07.25.Tue.)

■ 京都大学所蔵資料でたどる 文学史年表 　(2017.09.03.Sun.)

■ 高校数学の美しい物語～定期試験から数学オリンピックまで800記事

「最大公約数と最小公倍数の積はもとの二数（自然数）の積に等しい」（定理） (2017.09.18.Mon.)

■ 生活や実務に役立つ高精度計算サイト 　：数学公式集など。by CASIO (2017.10.04.Wed.)

■ 中学高校 英文法 　by 楽天市場 (2017.10.15.Sun.)

■ マナペディア 中学 高校 ５科目(2017.10.17.Tue.)

マナペディア(manapedia)とは、中学校・高等学校で勉強する科目に特化した、マナビを共有し合う場です。 ユーザーアカウントを作

成すると、テキストの投稿やマイリストの作成などができます。

たくさんのテキストの中からあなたにあったマナビを探したり、あなたが学習・勉強してきたマナビを形に残したりしてみましょう。

あなたの大切なマナビは、世代や地域をこえて、多くの人のためになります！さぁ、今すぐ始めましょう！

■ 金曜ドラマ ドラゴン桜 　by TBSチャンネル（TBSが贈るエンターテインメントチャンネル）(2017.10.24.Tue.)

■ 「ビリギャル」１年で偏差値を４０上げて慶應大学に現役合格した話 　(2017.10.24.Tue.)

一人の教師との出会いが家族の運命を変えた。感動の嵐を呼んだ、笑いと涙の実話が書籍化！

■ 映画 「ビリギャル」 　(2017.10.24.Tue.)

■ 入試が変わるって、どういうこと？ 　by Z-kai　(2017.11.06.Mon.)

■ 【業務向け】地図上の距離計測（クリックして算出） 　(2017.11.11.Sat.)

■ 【保存版】三角形の合同条件と相似条件の6つのまとめ 　by Qikeru　(2017.12.13.Wed.)

■ 大量の古典助動詞が一瞬で覚えられる！究極の覚え方とは？ 　by 大学受験.net　(2017.12.29.Fri.)

　現役東大生が勉強法を解説！大学受験.net

■ Wraymer 顕微鏡用デジタルカメラ by レイマー　(2018.02.01.Thu.)

■ 平成29年度入試（11期生と過年度生）全合格状況 平成29.4.5現在　by 県立広島高校HP　(2018.02.06.Tue.)

■ 科学実験！鉄球とネオジム磁石をぶつけてみよう！[科学でワオ！365] by ワオ・コーポレーション　(2018.02.8.Thu.)

■ 軽自動車検査協会　検査予約システム (2018.02.26.Mon.)

■ 今すぐ受検してず～っと役立つ！みんなで学ぶ「漢検」 (2018.03.03.Sat.)

平成30年度第１回個人受検　受付開始日　3月1日（木）、申込締切日　5月17日（木）、検定日　平成30年6月17日（日）

●● 以下【その２】へ。

当サイト TOP へ


【１】 【２】 【３】 【４】 【５】

‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥

© Rakuten Group, Inc.
X

Mobilize your Site
スマートフォン版を閲覧 | PC版を閲覧
    Share by: