私の問題解決の考え方 第3章2
今年は年賀状の着くのがずい分遅れました。いつもは3日までにほとんどの年賀状が着くのに、今年は、少しずつ来続けて、最後(だと思いますが)は12日でした。
今年は、どこも寒く、雪のところも多いので、これが原因かなと思っていたのですが、この間の新聞によると、「遅出し」が多かったのだようです。つまり、12月31日とか元日に出す人が多くて、郵便局には想定外のことで大変だったそうです(なぜだか分からないそうです)。
一方、私も出し方も変えて、今回は出す量を半分以下に減らしてしまったのでした。それでも、沢山の年賀状をいただいてしまい、結局、「後出し」で年賀状を出しました。
確率に関係して、年賀状の出し方について考えてみましょう。出し方をそれぞれの要素に分けるとき、同類のもの同士で違うものに分けなければいけないのです。
例えば、人間の場合、先生と女性を、同じ仲間の中の別のものにすることはできないのです。女性で、先生であることが可能なのです。女性と先生は、同類とは言えないのです。女性なら、性別ですから、後は男性しかありません。先生は、職業ですから、他に、弁護士とか、コックとか、医師とかがあるのです。
今度の場合、「遅出し」は、出す時期についてのものなので、後は、「ちょうどいいときに出した」、「早出し」でしょう。そして、「後出し」は、相手に対しての出す順序ですから、他の可能性は、「先出し」と「同時出し」になるでしょう。
<新しい証拠による確率の変化>
もう一度、1つのコインを投げたとき、表の出る確率を考えてみましょう。
可能性は2つ(表か裏)で、起きる可能性の全てですので、両方の確率を足すと1(全ての可能性)になります。そして、どちらの方が大きいという情報がなければ、両方とも1/2(0.5)であるということになります。
これは私が求めた確率ですが、私と同じような考え方をする人が求めれば、同じ値になります(この場合、かなり客観的と言えるでしょう)。
この検討で、与えられた課題が、表の出る確率を上げるということだったとしましょう。0.5という確率が得られただけでは何にも分かっていないと言われるかもしれません。
しかし、最初、この件についての知識が全くなかった(コインがどういうものか知らない、表も裏も分からない、可能性が表と裏だけだということも知らない等)とすれば、これだけでも、大変な進歩なのです。確率が0.5というのは、大きな値と言えます。何回か挑戦すれば、半分ぐらいは成功するということです。多くの問題では、成功する確率が非常に小さいのですから。
少し実験でき、新しい証拠が得られれば、もっと有利になる可能性があります。
以下、何か情報が得られた場合の確率について考えてみましょう。
神様が、今度は表が出るよと教えてくれたとします(嘘をつかないで)。そうすると、話は変わってしまいます。即ち、確率は1になります。このように、確率は、新しく得られた情報(証拠)によって変わってしまいます。(なお、神様が教えてくれる場合、この確率は、1か0にしかならないのです。)
例4 5回表が続けて出たら?
もう1つ、違う場合について考えましょう。今度は、神様は何も教えてくれませんので、初めは、表の確率は0.5です。しかし、5回コインを投げたら、5回とも表だったとします。
この結果を見ると、確率0.5で表が5回も続けて出る確率は0.5x0.5x0.5x0.5x0.5=約0.03になります。つまり、5回続けて表が出る確率は3%ぐらいしかないのです。
そうすると、この新しい証拠により、初めに0.5だと思った確率の値を疑わなければいけません。確率が0.5より大きいのではないかと考えられます。
同じコインでも、このように、新しい情報や証拠により、確率はいろいろ違う値になるのです。ですから、この確率は、コインだけによって決まるものではなく、確率を考える人の知識(分からなさでもいいです)の度合いと考えた方がいいのです。
<ギターは弾かなきゃ音がでない!>
これは、日本でエレキギターを始めた寺内タケシさんの言葉です。
私がここのところ言ってきた、
「まんずやってみれ!」
と同じことだと思います。
今朝、NHKテレビで、この人が、無料で、長年、学校でコンサートを続けてきた話を聞いて感動しました。大きなバス1台に、バンドのメンバーや道具を全部乗せて、学校へ行き、子供達や父兄の前で演奏するのです。
寺内さんは、多くの出会いを通して、日本の子供は思ったほど悪くない、まだ希望が持てると感じた、と言っていたと思います。私も同感です。大人の方こそ心配です。
私が感心したのは、この人がとても謙虚なことです。長い間ギターをやっているのに、まだ自分の技術に満足していないのです。毎回、まだ入り口が見えないと言っているのです。
それに比べて、ある、かなり有名な女性バイオリニストは、朝のNHKのドラマ番組のはじめの音楽での自分の演奏について、満足に弾けたと言っていました。(しかし、私は、毎日、そこの部分の音量をいつも小さくしていました。)
<大事なことは可能性の認識!>
問題解決にとって大事なことは、問題点の洗い出し、つまり、解決につながる要因をまずいろいろと考えることです。検討を始める前にも、やりながらも、問題に関係がある、いろいろな要因の可能性を考えることです。
問題解決のために、私には、確率・統計の勉強が役に立っています。つまり、各種確率を定義しようとすることです。そのためには、いろいろな要因を「重複することなく、抜けがないように」見つけなければなりません。
解決の初期では,抜けがない(大事なことが漏れていない)ということが特に大事です。初めは、あまり重複のことは考えなくてもいいです。
実際の検討を行ないながら、大事な要因だけに絞るようにしていけばいいのです。
<元気があれば何でもできる!>
これはアントニオ猪木さんの言葉です。
健康で、元気な、前向きな姿勢で問題に立ち向かえれば、大抵の問題は解決できると思います。
<私には信仰も自信もありませんが、・・・>
でも、危なくなると頑張ります。いや、危なくならないと頑張らないのかもしれません。試験の前の一夜漬けと似ていますが。苦しくなってからやっと本気になるのかもしれません。
神様や霊が存在するかどうかは分かりません。自信を持てるかどうかも分かりません。しかし、次のことは謙虚に受け止めています。いや、はっきりと知っています。
人間にはできないことが沢山ある。
人間には知らないことが沢山ある。
人間はかなり傲慢である。
ですから、人間の私が、何かができるとか、何かを知っているとか、言い切ることは、とても難しいのです。だからと言って、 難しい問題に出会っても、できないとは思ったことはありません(できるとも言えませんが)。やってみなければ分からないではありませんか。
<研究もホリスティック?! >
代替療法の本で「ホリスティック(holistic)」という言葉を覚えました。「総合的、全体的視野からの、全身の」というような意味だそうです。
私達の研究も、そうでなければなりません。自分の専門のことだけに拘って、他の分野で分かっていることに気づかないような研究者がかなりいるのです。
そう言えば、お医者さんだって、自分の専門分野のことだけしか考えないような人が相当いるようです。
自分のことを考えてみると、名刺の肩書きには「研究員」とあり、会社にいるほとんどの期間にわたって、「研究」を続け、論文も書いてきました。講演や講義もしました。しかし、自分を専門家だとも、学者だとも、先生だとも思ったことはなく、いつも素人気分だった(分からないことだらけ)と言えます。また、自分で自ら実験を続けることができたので、世の中には、人間の分からないことが沢山あるということを身をもって学びました。ですから、私は、「分かりません」と平気で言えるのです。
研究とは、分からないことを少しでも分かるようにすることだと思っています。そのために、これまで、私はいろいろな分野の人達の助けを借りてきました。研究者でなくても、私の秘書係の女性とか、我が家の娘達とか、研究と関係のない知り合いなどにも助けてもらっています。
今、このようなことを思い出しながら、論文をまとめようとしています。結局は、子供のような心を持ち、初心に帰って、問題解決に立ち向かうことだと思います。いわゆる「専門家」の言うことを鵜呑みにしないで、自分で考えて、判断、行動する癖をつけることです。
その結果、自分がひとっきりやっている、あるいは、やったことについては、他の人に比べたら、真実を知るようになれると思います。
<木を見るより森を見よ?>
これは、細かいところばかり見て、全体を見ない人への戒めとして、私も正しいと思います。しかし、・・・
何も分からない人が森ばかり見ても何も分かりません。馬鹿医者が急に患者の全体をよく見ようとしても何も分からないでしょう。木を見ることもできない人に森を見よと言っても無駄でしょう。森は木の集まりなのです。言われた人はますます駄目になるでしょう。
独りよがりの目で、木を見ないで、森を見る(ていると思い込む)のはもっと悪いです。分からないことを分かっていると思うことになりかねません。
これで思い出すのが、米国によるイラクやアフガニスタンの空爆です。アメリカ人が1人の無抵抗のイラク人を鉄砲で撃ったら大変なことになるでしょう(米国でも)。しかし、森を空から見るみたいに、上から下を見て空爆し、大勢の民間の人が亡くなっても、やむを得ないことだったとか言うのです。こんな理不尽なことがあるのでしょうか。
<問題解決には本気、やる気と緊張感・・・根性も!>
新製品の開発などで、よほど本気で、やる気と緊張感がないと、複雑で難しい製造技術などを立ち上げることは難しいのです。
私達の研究でも、大事な問題点を見逃してしまったり、技術の制御がなかなかできなかったりなど、非常に手間がかかってしまうことがあります。
これらの仕事に携わる人達が本気になって、緊張感のある状態にないと、つまらないミスや抜けができ、多大な労力や時間(勿論お金も)の損失になるのです。
お役所が関わっているいろいろな事業だって、そうだと思います。多額の税金を使って作った施設などが、利用者が少なくて赤字になって、二束三文で売られたりしているのです。
浅田真央さんは、今度の大会では4回転を成功させたいと言っています。大人達も少しは真似をして、気合を入れて仕事をしてもらいたいです。この前、ミスなしで優勝したとき、「根性だ」と言っていたと思います。大したもんだ!
<感謝の気持ち>
私は、1週間に1回、母のところへ行って、いろいろ悩みごとを聞いてきます。東京の汚い空気を吸い、息苦しくなり、のども痛くなるので、あまり乗り気ではありませんが、私のためにもなっているのです。
まず、「母の相談に乗っている」(私の問題解決研究所の仕事だと)と考えることで、前のように、怒鳴り散らさなくなりました。また、母の問題についても、前より冷静に対処できるようになりました。
また、最近は、前のように、私鉄の駅からバスに乗ることは止めて、もっと手前の駅で降り、歩くことにしました。ちょっと歩きますが、歩くと気分がよくなり(比較的排気ガスが少ないので)、運動にもなるのです。歩きながら、いろいろなことも考えられます。
往復の電車(歩くのを加え、合計4時間以上)でも、いろいろなことを考えたり、見たり(たまには美人を)できます。音楽を聴くこともできます(私の音楽の勉強と、他のことを考える助けになります)。
昨日など、合計2時間半ぐらい歩きました。去年の骨折以来、体が弱ってしまったのですが、これで、ほぼ回復したと思いました。
帰ってくると、のどが少し痛いですが、母の様子を見に行くことは、私のためにもなっていると思います。感謝です。
<堀江元ライブドア社長取締役辞任・・・自信とは?>
やはり悪いことをしたと「思って」いるのでしょうか。いや、法を犯したと「思って」はいないと言っているようです。この「思って」というのが曲者なのです。他の会社の社長さん達も、脱税で摘発されたりすると、よく、そのような「認識はなかった」と言います。同じようなことです。見つからなければいいと「思って」いるのでしょうか。
探偵小説にも、殺人者は、罪を重ねて行くうちに、悪いことをしているとは「思わなくなって」いくと書いてあります。悪事がばれないと、もう少しやってももばれないと「思う」のかもしれません。また、自分のやっていることを悪いと思わなくもなっていくのでしょう。
一方、私の論文で考えていることにも似たような要因が含まれています。
確率とは、
「何かが真実である、何かが起きるなどと受け入れる、認識する、考える、信じる、思う度合い」
なのです。
ですから、確率を使う(が使われる)とき、このことを忘れてはいけないのです。確率の値を示されると、それが客観的な事実を示しているものだと「思い込んで」しまうかもしれません。また、どういう条件でそう「思って」いるかの説明も不十分な場合が多いのです。言葉の意味が正確でないこともあります。「確率で嘘をつく」こともできます。
以上のことから、また、「自信」について考えてしまいました。自信とは、できると「思う」こと、信じることです。どのくらいの確率だったら、自信なのでしょうか。私には分かりません。
去年暮れに、堀江元社長がライブドアを世界一にするとかと言ったときはどうだったのでしょうか。かなり自信ありげでした。できると「思って」いたのでしょうか。そう「思い込んで」いたのでしょうか。
そう言えば、細木数子さんだってそうです。人の未来について、やるべきことについて、断言できるのです(断言だけなら、私の女房だってできます)。私なんか、自分のことも分からないのです。ましてや、他人のことなど。ところで、彼女(細木さん)は、堀江元社長にとって、今年がそんなに悪い年だとは言っていなかったような気がします。まだ、今年は長いので、釈放されて、盛り返すのかもしれませんね。
<やっと説明できるかな?> (1月26日)
論文「私の問題解決の考え方」の第3章「問題解決と確率・統計」の一番大事なところでもあり、説明の難しいところについてずっと考えていました。そして、昨日、それができそうな気がしてきました。それから、説明の例の中で、確率の意味についても、問題解決でもっとも大事なところでもあり、難しいところの指摘もできそうな気がしてきました。
やりたいことは、確率・統計の「条件確率」と「ベイズの定理」を一般の人に分かるように説明することです。
こんな風に始めましょうか。
私の問題解決の考え方が正しいかどうかを見るために、なんと、3万人の人を動員して、同じ問題の解決を試みてもらいました。
例5 3万人の問題解決の調査
ある問題の解決に、3万人の人達が挑戦しました。その結果、16,200人が成功し(この集団を「Y]と名づけます)、13,800人(この集団を「N」と名づけます)が失敗しました。
1.成功した人達「Y]16,200人のうち、
1)2,700人が「まんずやってみれ!方式」(第2章参照)を使って(M)いました(いろいろな可能性をまず試して、問題点や解決策の洗い出し、目的ややることを具体化し、計画を立てて、実行しました)。この集団を「M∩Y」と名づけます。つまり、成功して、かつ(∩:and)、「まんずやってみれ!方式」を使った人達(M∩Y)の集団という意味です。
2)13,500人がこの方式を使いませんでした(NM)。この集団を「NM∩Y」と名づけます。つまり、成功していて、この方式を使わなかった人達という意味で、「NM∩Y」と書きます。
2.失敗した人達「N]13,800人のうち、
1)300人が「まんずやってみれ!方式」を使って(M)いました。この集団を
「M∩N」と名付けます。
2)13,500人がこの方式を使いませんでした(NM)。この集団を「NM∩N]と名づけます。
以上が調査結果をまとめたものです。(ここで、各集団を英語の略号で分類して、ちょっと分かりにくくなっているかもしれませんが、これは、後で、大事な定理を説明するためですので、我慢願います。)
さて、これらの結果を踏まえて、知りたいことは、3万人の人達がどのような計画の立て方で、どのように成功あるいは失敗したかです。言い換えると、結果(成功か失敗か)から原因(「まずやってみれ!方式」を使ったかどうか)への流れを調べて、逆に、原因から結果への流れを知ろうとすることです。
この問題が分かれば、結果から原因の推定、および、原因から結果の予測が原理的にはできることになります。ここいらの状況を図で表そうとしています。
以上は調査結果のまとめです。この結果から、原因について何が分かるでしょうか。
上のように、文で書くとちょっと分かりにくいかもしれませんが、同じことを図3.1のように表すと、より分かりやすくなります。
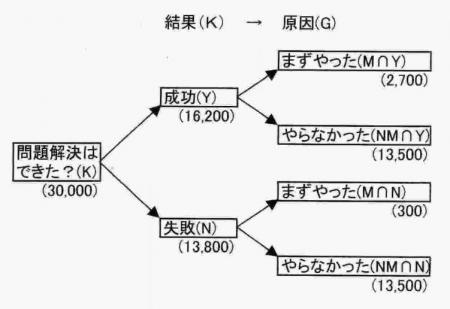
図3.1 結果から原因への分析
この図から分かることは、
1.「まんずやってみれ!」方式を使った人は、「M∩Y」と「M∩N」の人、計3,000人で、全体30,000人のうちの10%でした。
2.この方式を使った人3,000人のうち、問題解決に成功した人「M∩Y」は2,700人で90%でした。
3.一方この方式を使わなかった人「NM∩Y」と「NM∩N]の人、計27,000人のうち、成功したのは、13,500人の50%でした。
まとめると、「まんずやってみれ!」方式を使った方が成功する確率が高い(90%対50%)のですが、全体のうち10%しか、この方式を使っていませんでした。(これは、後からの種明かしですが、実は、15,000人に、予め、この方式を使ってみたらと勧めていたのです。つまり、言うことを聞いてくれたのは20%しかいなかったのでした。)
<原因 →結果のまとめ・・・・・・条件確率> (1月29日)
以上の結果(まとめの最後のカッコ内は除く)を図にしてみましょう。元のデータは同じです。ちょっと整理して足し算をするだけで、図3.2が得られるのです。
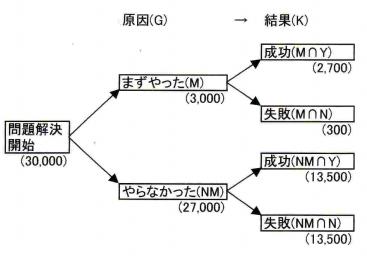
図3.2 原因から結果への解析
図3.1では、結果から原因への流れを図にしました。それを、今度は、逆の、原因(「まずやってみれ!」方式を使ったかどうか)から結果(問題解決に成功か失敗か)の図にしたのです。
それには、まず、図3.1の一番右の列で、「まんずやってみれ!」方式を使った人と使わない人の数を求めました。両方とも、成功と失敗の場合の数を足して、それぞれ、3,000と27,000人になりました。そして、この方式を使った場合と使わない場合について、それぞれ、成功と失敗して人の数を書けば終わりです。
結果から原因の解析(図3.1)で、私は、成功確率は「まんずやってみれ!」方式を使った場合の方が高いと書きました。図3.2で、成功した人の数を見ると、この方式を使わなかった場合の方が多いのです(13,500と2,700)。では、なぜ、確率が前者で大きいのでしょうか。
それは、この方式使用の有無の場合の数が違うからです。確率を求めるには、「まずやってみれ!」方式を使った場合は3,000で、使わなかった場合は27,000で割らなければなりません。そして、それぞれ、0.9と0.5という確率(とても大事な結果)になります。
これらの確率は、同じ「成功確率」なのですが、全体の「成功確率」0.54とは違います。この場合(全体)は、成功した人(Y)の数も、総人数も、この方式を使った人も使わなかった人も含めた合計(全体)数、16,200と30,000人を使っています。この、全体の成功確率を、数学の記号では、P(Y)と表します。
ここで、0.9という確率は、「まんずやってみれ!」方式を使った(M)という条件での成功(Y)確率なのです。これは「条件確率」と言って、P(Y|M)と書きます。
そして、0.5という確率は、この方式を使わなかった(NM)という条件での成功(Y)確率なのです。こちらの条件確率はP(Y|NM)と書きます。
この世の中の確率はほとんどが条件確率と言えるでしょう。しかし、どのような条件であるかをはっきり言っていない場合が非常に多いのです。このことが原因の一つで、素人の私達は、確率・統計を持ち出して説明されると、しばしば騙されてしまうのです。これがいわゆる「統計の嘘」と言われているものの一つです。
図3.2で何をやったかと言うと、見方を変えただけです。表3.1で説明しましょう。
表3.1 3万人の問題解決のまとめ
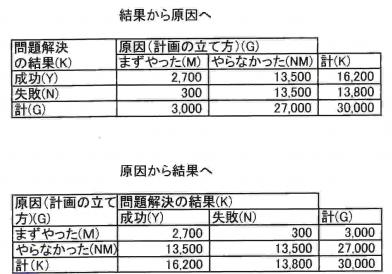
まず、上の、「結果から原因へ」で、調査の結果を表に表わしました。成功と失敗の数を一番右の列に書き、それらの内訳を「まずやった」と「やらなかった」の列に書きました。それぞれの合計を一番下の行に書きました。これは図3.1を表で示したものです。
そして、図3.2を表にしたのが、下の表「原因から結果へ」です。この表を求めるには、上の表で、縦と横を入れ替えただけです。これだけのことで、図3.2に示した、まずやった確率と、まずやったという条件の下での成功の確率(条件確率)などが求められるのです。
これができたのは、2,700人が、まずやった人の中で成功した人の数とも(上の表)、成功した人の中でまずやった人(下の表)とも言えるからなのです(これが次項で説明する大事な定理になるのです)。それから、勿論ですが、調査で、ただ成功と失敗の数を調べただけでなく、それぞれの内訳(まずやった人とやらない人)も調べたからです。即ち、漫然とではなく、きちんと調査すれば、いろいろなことが分かる可能性があるということです。
<ベイズの定理と条件確率>
最後に、これまでの図や表を一つの図で表して、これまで説明してきた各種確率の値を示しましょう。そして、分かったことをまとめましょう。
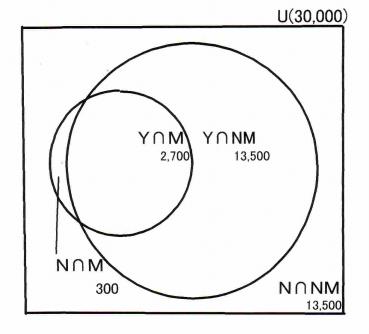
図3.3 調査結果のまとめ(Venn図)
図3.3はヴェン(Venn)図というものです。ヴェンというのは、イギリスの数学者(牧師でもあった)の名前で、この人が、いろいろな場合同士の関係を表すために考えたものです。
この図で、まず、長方形が全体U(30,000人、この数を母数にした確率にするとP(U)=1)を表します。この中に2つの重なった円があって、長方形が4つの領域に分けられています。
それらの領域の面積がそれぞれの部分の確率(30,000人を面積1としたとき)になるようにするのです(この絵では正確にそうなっていませんが)。
左の円の中は「まんずやってみれ!」方式を使った確率P(M)です。2つの確率、P(Y∩M)とP(N∩M)を足すとP(M)になります。ここで、Y∩Mとは、成功して(Y)、かつ(∩)、「まんずやってみれ!」方式を使った(M)という意味です。Mは「まんずやってみれ!」方式を使った集団、NMはこの方式を使わなかった集団、Yは成功した集団で、Nは失敗した集団です。
一方、右の大きい円の中(面積)は、成功した確率P(Y)です。2つの確率、P(Y∩M)とP(Y∩NM)を足すとP(Y)になります。
さて、ここで、Y∩Mの領域に着目してみましょう。ここは、成功の集団の円Yの一部とも言えますし、「まんずやってみれ!」方式を使った集団の円Mの一部とも考えられます。
このことから確率の大事な定理、即ち、ベイズ(Bayes)の定理、を導くことができるのです。
まず、成功Yの立場から見ると、成功したという条件の下で、「まんずやってみれ!」方式を使った条件確率P(M|Y)は
P(M|Y)=P(Y∩M)/P(Y) (1)
で、Y∩Mの部分の面積を右の円(Y)の面積で割ったものです。
一方、「まんずやってみれ!」の立場から見ると、その方式を使った(M)という条件の下での成功Yの確率P(Y|M)は
P(Y|M)=P(Y∩M)/P(M) (2)
で、Y∩M(成功して、かつ「まんずやってみれ!」方式を使った)の面積を左の円(M)の面積で割ったものです。
そして、これらの式からP(Y∩M)を消去すると、
P(M|Y)P(Y)=P(Y|M)P(M) (=P(Y∩M)) (3)
になります。これがベイズ(Bayes:18世紀のイギリスの牧師で数学者)の定理です。
さらに、右の円の面積P(Y)、成功の確率は
P(Y)=P(Y∩M)+P(Y∩NM)
=P(Y|M)P(M)+P(Y|NM)P(NM) (4)
そして、左の円の面積P(M)、まずやってみれ!方式を使った割合P(M)は
P(M)=P(Y∩M)+P(N∩M)
=P(M|Y)P(Y)+P(M|N)P(N) (5)
になります。
(3)式のベイズの定理を使って、表や図から既に解いた問題に再挑戦してみましょう。式に与えられた確率の値を代入するだけで答えを得ることができます。
今回の問題(結果 →原因から原因 →結果を求める)では、
与えられたものは、確率に直して、
P(Y)=0.54、P(M|Y)=0.1667、P(M|N)=0.02174
です。[P(N)=1-P(Y)、P(NM|Y)=1-P(M|Y)、P(NM|N)=1-P(M|N)です。]
求めたいものは、P(M)、P(Y|M)、P(Y|NM)などです。
まず、(5)式から
P(M)=P(M|Y)P(Y)+P(M|N)P(N)
=0.1667x0.54+0.02174x0.46=0.1
次に、
P(Y|M)=P(M|Y)P(Y)/P(M)
=0.1667x0.54/0.1=0.9
と
P(Y|NM)=P(NM|Y)P(Y)/P(NM)
=0.8333x0.54/0.9=0.5
になります。[P(NM)=1-P(M)、P(N|M)=1-P(Y|M)、P(N|NM)=1-P(Y|NM)]
これで終わりです。
しかし、確率の式や値だけを見ていると、それらの意味が理解できない場合があるのです。これまでやってきたように、それぞれの場合の数にして表してみると(もし表わせるなら)、分かりやすくなります。
さて、以上の検討では、結果を調査、解析することにより、その原因について知ることができました。
しかし、一般には、このような検討は、何かの課題を解決するためにやるのです。ここでは、問題解決について考えているので、例えば、
「解決の成功確率を上げたい」ということを課題にしてみましょう。
上のベイズの定理というのは、ある意味では、人間が考えるのと似たような結果を出してくれるのです。上の例で、最初は、「まずやってみれ!」方式を使っている割合P(M)は0.1(10%)です。
上の計算の結果の一つとして、P(M|Y)=0.1667というのがあります。これは、成功するためには(Y)、確率(Mの割合)を0.1667に(増やしたら)したら、という示唆として受け取れます。一方、P(M|N)=0.02174ですので、失敗のためには、M(「まずやってみれ!」方式)の割合を減らせ、ということなのです。
そこで、Mの割合を0.1667(これを確率の更新と言います)、即ち、「まずやってみれ!」方式を使った人の数を5,000人(30,000人のうち)にしてみましょう。そうすると、
P(Y)=0.9x0.1667+0.5x0.8333=0.5667
P(M|Y)=0.9x0.1667/0.5667=0.2647
になります。確かに、成功の確率が0.5から0.5667に上がりました。そして、今度はMの確率をP(M|Y)=0.2647にする(Mを増やす)と、成功確率も0.6059になります。この過程を表にすると、次のようになります。
回数 Mの割合P(M)またはP(M|Y) 成功確率P(Y)
___________________________
1 0.1000 0.5400
2 0.1667 0.5667
3 0.2647 0.6059
このように、Mの割合を増やしていくと、成功の確率は次第に増加していきます。そして、Mの割合を100%にしたとき、成功の確率は最大の値0.9
(90%)になります。
<ここ2、3日考えたこと> (1月30日)
上記の説明を考えながら、確率・統計について、考えたり、再認識したことを以下に書いてみましょう。
世の中は分からないことだらけ。確かなことは、私達がいつかは死ぬということぐらいです。だから、確率・統計という学問があるのです。
確率・統計は、単に、「常識」を数学の言葉で表そうとしただけのものなのだそうです(フランスの数学者ラプラスの言葉)。ですから、これだけでは、問題の答えは教えてもらえないのです。しかし、私達が問題解決のために考えるのを助けてくれます。
分からないことがあるのは当然。怖がったり、恥ずかしがることはないのです。ただ、分からないと言って、初めから諦めて何もしないのは最悪です。
何かが分からないとき、どう対処するかが大事なのです。分からないことに関し、できる限りよく調べ(実際に実験するのかもしれません)、よく考えると、何が分からないかがまず分かってきます。そして、自分の体と頭をよく使うと、思ったよりも分かってくることが多いのです。
できるだけ沢山の証拠を集めて、よく考えることにより、ある結果から原因を推定したり、また、逆に、原因から結果を予測したりすることも不可能ではないのです。確率・統計の問題としては、どちらも同じことです。
一番大事なのは、いろいろな可能性について考えるところです。抜けがなく、重複しないように洗い出したいのですが、
☆同じものでも違う分け方(捉え方の違い)がある(問題解決でも、解決法で分類することもできるし、その結果で分類することもできる)。
☆まず全部洗い出し、その中からもっと重要なものに絞る。
☆なるべく簡単な形にして考える。
新しい情報が入ったり、証拠が明らかになったりするたびに状況は変わるのです(例えば、問題解決の成功確率の値は変わるのです)。これらの新事実に対応して、やることも変えて行かなければいけません。
同じことでも、違う角度から見ると、新しいことが分かることがあります。
確率・統計の考え方は、人間もこのように考えた方がいいと思われるようなものです(だから「常識」とラプラスが言ったのです。良識と言ってもいいかもしれません。)。それを人間がやるかどうかは別ですが。
<捉え方の違い>
今回の耐震強度偽装は正にその例です。
マンションを「作った」建設会社、設計事務所、施工会社、販売会社など皆悪いことをしていたのです。彼等は見かけは良くて、他より安いマンションを売って儲けようと思っていたのです。安全性に問題があっても、法律は守らなくてもいい、という条件でやったのです。
一方、買う方は、「見た目が良く、安い」マンションを買ったのですが、そのとき、安全性に問題があることはないと思ってしまったのでしょう。ちゃんとしているらしい会社が売っているものだから大丈夫だと思ってしまったのでしょうか。
「顧客の捉え方」と「業者の捉え方」に大きな違いがあったのです。同じマンションなのですが、お客には「快適な生活の場所」なのですが、これらの業者には、「金儲けの手段の一つ」でしかなかったのです。
この世の中、本当に油断できませんね。鵜呑みは絶対駄目だと思いました。
< 美味しい!> (2006.1.30)
また蕎麦掻きを作りました。今度は、この間のような、いい粉ではありませんでしたが、かなり美味しいものができました。辛い大根おろしと山葵で食べました。食べた後の気持ちもいいです。
もう一つ美味しいものを食べました。秋田の朝市で買ってきた、白花豆を女房が灯油ストーブの上で煮てくれました。この味が最高でした。
Re:美味しい!(01/30) M,S、るんるんさん からのコメント
>蕎麦掻き、白花豆の事を読んで少しホットしています。
私の答え、
>こういうものを食べると、安心するというか、ほっとしますね。
ルンルンさん、
>統計、確率の事は分かるようで分からなくて、まして計算にして出してしまえる岩田さんに感心しています。
また、読んでいて印象に残ったことは鵜呑みにするなです。
私、
>るんるんさんは、確率・統計の一番大事なところは、既に身につけていらっしゃると思います。
るんるんさん、
>私は一人一人が当たり前のことをキチンとやれば人を疑って見たり要らない思惑をもたないで、また、ある程度鵜呑みにしても良く、心汚すことなく世の中が回っていけるのに、これも致し方の無いことなんですよね
巧くは言えませんが、少しの欲がなければこれもまた生活して行けませんし難しいなぁーー
私、
>あまり疑い深いのもいやですね。なんでも「良い加減」がいいのでしょうね。
るんるんさん、
>それに、奥さんが買ってきたという石油ストーブいざと言うときの為に私も確保しています。
便利は不便と言う事がありますが、電気が消えたりしたときにオール電化だと秋田の冬では寒くて心細くなりますがシンプルなものが最後は役立ちますね。
私、
>我が家はオール電化で、停電のときが心配です。電気がいらない石油ストーブはあります。
<鵜呑みは駄目よ! >
は、
全ての可能性を考えなさい、
いろいろな可能性を考えなさい、
抜けがないように可能性を考えなさい、
などということに通じると思います。
私が確率・統計を学んでから、肝に銘じていることです。
以下は、そうしないように注意していることです。
自分が何かをこうだと思いこむ、
人に言われたことをそのまま信じる、
先生や地位の高い人が言うことは正しいと思う、
自分はある分野の専門家、学者、研究者だと自認する、
素人の意見を馬鹿にする、
結論はこうなるはずだと考えて研究をする、
などです。
最後の点は、「仮説を立てて実験をせよ。」と学校などで教えていることに反しますが、私は、ある仮説のことだけに絞ってしまうことを心配しています。例えば、警察が誰かを犯人だと決め付けてから捜査をすると、犯人だということと矛盾がないことしか探さなくなる可能性があるのです。犯人ではないという可能性もあるのにです。
<チェック機能は猫以下?? >
日本の、人間のチェック機能が心配です。
私が、これまで、研究で常に見つける(そして用いる)ようにしてきた「チェック機能」は、研究以外でも、とても大事です。
今回の東横インの違法行為は、会社ぐるみのようです。会社の中では、まったくチェック機能がなかったようです(それどころか悪いことを良いとしていた)。そして、違法ホテルの一つは、15年前に自治体から違法が指摘されていたのです。それなのに、元に戻した確認ができていなかったのです。これは自治体にも責任があります(他のホテルでも)。
また、マンションの耐震強度偽装の件で、販売会社ヒューザーの小島社長が、なんと、自治体がちゃんとチェックしていなかったと提訴したのです。良心的な販売会社なら、自分が売るものが安全かどうかぐらい分かるはずです。この社長は安全でないことを多分知っていたと思います。設計会社、建設会社、設計事務所、施工会社、チェックする機関も皆仕事をちゃんとやっていなかったのです。
我が家のトラは猫なのに、音楽の良し悪しが分かるみたいです。この間、私がいよいよアコーディオンの練習を始めようとしたら、部屋から出て、2階へ行ってしまいました。また、女房が大正琴を弾くと、声や手(足)を出して止めろと言います。さらに、刺身の鮮度についてなら、普通の人間よりずっとよく分かります。もしかしたら、猫の方がいろいろな良悪の判断がちゃんとできるかもしれませんよ。
この「チェック機能」というのは、確率を求めるのにも、大事なことです。即ち、問題解決にとっても、大変重要です。
<会社は別の社会?>
東横インの違反行為は70以上のホテルで行われていたそうです。横浜でも、違反を指摘されていたのに、何年も放置されていたとのことです。中田横浜市長が東横インを非難していましたが、違法行為を放置していた横浜市はどうなっているのでしょう。
やめさせなければ、チェック機能になりません。
120の東横インのうち、70以上の違反ホテルの支配人(と言うのでしょうか)や他の従業員は、検査後の改築を見てどう思っていたのでしょうか。この会社の中では、こうすることが悪いという認識がなかったのかもしれません。
会社ではありませんが、学校でも似た経験があります。ある大学で、ある教授が、普通の社会では良くないことをやっていました。しかし、管理職?である学科長とか学部長は、止めさせようとしないのです。また、この行為が外部の会社に関係しているので、そこから抗議されたら、学校が責任を取るのかと聞いたら、学校は一切取らないと言うのです。責任は、その教授個人にあるのだと言い張っていました(契約は学校とその会社になっていましたが)。
このときは、会社の方がいいと思いましたが、あまり変わっていないということでしょうか。
<猫の方が上なのは当然?>

一昨日でしたか、人間と猫を比べましたが、格が違っていたのかもしれません。
西洋では、猫は、精霊との連絡係とも、精霊そのものともされているようです。そして、魔女に付き添っている絵なども見たことがあります。イギリスは、スピリチュアルのことでも分かるように、この分野では進んでいる?ようです。
病気を治してくれたり、天気を教えてくれたりすることもあるようです。
[以下2014記]
トラ(写真)は、生まれてまもなくわが家に自分で来て、ほぼ20年生きました。そして、自分の頭と体だけで、生きたいような一生を送ったと思います。
私は動物はあまり好きでないのですが、家の窓のすぐ外にいたのを娘と女房が中に入れてしまったのです。そこで、仕方なく、私が、風呂に入れ、きれいに洗ってやり、牛乳を飲ませたりしたら、なんとか元気になってくれ、わが家に居ついてしまいました。娘達には、飼うなら、一生面倒を見ると約束させ、飼うことになったのですが、結局、娘達の結婚後は女房が面倒を見ました。(結婚相手が猫アレルギーだったり、マンション住まいのため)
私にはくっついてこないように、なんとか躾けましたが、かなり勝手気ままな一生でした。
自分の食べたいものとか、居たい場所など がとてもよく分かり、拘束されるのを嫌がりました。飼い主でも、あまりべたべたされると、ひっかいたり、逃げたりしていました。ただ、トラの方は自分が好きな人なら、くっつきたいときには、くっついてくるのです。新しく会う人でも、好きか嫌いかが直ぐ分かるようでした。
驚いたことに、赤ちゃんには絶対に手を出しませんでした。上に乗っかったりもしませんでした。むしろ、守ろうとしてくれていたのかもしれません。泣いたときなど、呼んでくれるのでした。
好きな食べ物(魚)があると、寄ってくるし、古いものもよく分かるのは当然なのですが、私が食卓に座っていて、もうすぐ食べ物が出てくる頃に、トラも来ているのです。
私から見ると、頭はいいし、自分の好き嫌いの判断はしっかりできるし、自分の意志はしっかりと持っていました。そして、自分のやりたいように生きたと言えるでしょう。
一方、人間は、便利な機械や、確率・統計や巨大なコンピューターの力を借りても、望むような一生を送れない場合が多いのではないでしょうか。いや、何を望むかが分からないままに一生を終えてしまうかもしれません。
猫の方が人間より上?[ここまで2014]
<よく見るのが一番!? >
この頃、携帯にもカメラ機能が付いていて、とても便利です。私は、デジタルカメラの調子が悪くなったとき、携帯の機種を、良い写真が撮れるものに替えて、カメラは結局買いませんでした。
携帯で写真を撮るのは楽しいのですが、私は、肝心なときには、撮ることを忘れてしまうのです。友達にもそれをよく指摘されるのですが、見る方に神経が集中してしまうらしいのです。写真家の大石芳野さんも、子供の本当にいい表情など見ると、それに見とれて、写真を撮るのを忘れてしまうとのことです。
私のことですが、自分が食べたうな重だって、かなり前のことなのに、昨日のことのように、目に浮かんできます。そう言えば、12月の初めに食べた、アナゴのにぎりもすぐ目に浮かんできます(食べ物のことが多い?)。
一方、秋田で高級な料理屋さんへ行っても、あまりご馳走が多くて、何を食べたかはっきり分からないで終わってしまいました。途中で、写真を撮ればいいのにと言われたのですが、そのときは半分以上食べていました。
こんなこともありました。人間の目って、よく見ていると思わなくても、結構見ているのです。やはり秋田で、ある中学校の学園祭へ行ったとき、急いでいたので、さっと学校の中を一回りして帰ってきました。
ひとっきり経ってから、この学校は人数が多くて、いろいろな問題が起きているという話を聞いたのです。それで、行ったとき見たこと(意識していなかったのに)を思い出したのです。
思い出したことは、
受付のところに男の先生ばかり数人が並んでいました、
受付けも、先生で、男でした、
先生方に会うと、「お早うございます」と挨拶してくれるのですが、無理にしているみたいでした、
生徒がちっとも見えないのです、
そのとき、生徒全員は講堂の中でブラスバンドの演奏を聴いていなければならなかったのだそうです、
展示品の採点(何か賞が出るのでしょう)も全部先生がやっていました、
などでした。
どうも学校側が、生徒達がまとまるように、問題を起こさないように、「強く」指導をしていたらしいのです。それを知らないで私は学校へ行ったのですが、無意識に、なんだかおかしいと思い、頭のどこかにしまっておいたのでしょう。そして、後で、関連した話が出て、全部思い出したのでしょう。
人間の目と頭は「大したもんだ」と思いました。
<「確率」について・・・・・ただ1人とか1回の場合は??? >
-入学試験に受かる確率は?-
これまで、確率・統計について、長々と説明してきました。教科書のように、整理された書き方ではありません。私の頭の中から出てきた内容です。でも、その元は、教科書で読んだこと、自分が出会った問題で考えたことや、それらを応用したことなどです。
「分かりやすさ」ということから、「3万人の問題解決の調査」について考えてみました。というのは、何人中の何人、何回のうちの何回というように、数にして考えると、考えやすいし、確率の値(割合として)を求めることもできるのです。
しかし、・・・
実際は、3万人のことではなく、私のことが問題!
その問題は、多分一生に一度のものでしかないのです、
こんなとき、確率のことを考えられるのか、
私がうまくやるにはどうしたらいいのか、
この調査の結果が私の問題解決を助けてくれるのか、
など、いろいろな疑問が湧いてくるでしょう。
でも、・・・
私のような、1人の人間でも、そのときによっていろいろ変わるのです。何かをやらなくても、そうなっていなくても、いろいろな可能性があるのです。これらのことから、1人の人間の中にも、いろいろな種類の人間がいると考えることもできるのです。
時や場合によって、考え方がいろいろ変わる可能性があるのです。つまり、3万人の人の行動は、私の中のいろいろな面を表しているとも考えられるのです。但し、結果は、今回の調査結果とは違うかもしれませんが。
結局、こう考えてみてはどうでしょうか。
「今考えている問題が、自分の一生のただ1回の出来事であっても、問題を考えるとき、私の中のいろいろな可能性として、大勢の人間がいるかのごとく(人数の割合と)考えてもいいのではないでしょうか。そうすれば、考えやすくなります。確率の値そのものを求めるのは依然として難しいですが、高望みしなくてもいいのです。考える手順とか、考えるときの心構えなどを確率・統計から学ぶことができるのです。」
こんな風に。
「15,000人の人に、「まずやってみれ!」方式を説明し、使うように勧めました。しかし、3,000人しか実際に使ってくれませんでした。」
これを、
「私は、「まずやってみれ!」方式を勧められたのですが、結局、私の中の20%しかこの方式を使いませんでした。」
と考えるのです。
<研究も論文も書きながらまとめる? >
かつて、会社で研究していたときは、研究がまとまると、論文を書いていました。
ところが、今回は、研究が終わっていないのに、論文を書き始めてしまったのです。ですから、書きながら、私の考えも少しずつ変わっています。
特に、ここのところ、確率・統計の説明について、一所懸命に考えたら、研究(問題解決)の基本的な考え方の内容も少し変わったようです。
これは自然で、当然のことだと思っています。しかし、既に書いたことを変えるべきかどうかどうか、今、迷っています。明らかに間違っていることなら、訂正しなければなりません。それらは、気づいたときに、訂正します。
しかし、考え方の違いや進歩の場合は、そのままにしておこうかと思うのです。というのは、考え方が変わっていくということが、私の思考の進み具合を示してもいるからなのです。この論文を読みながら、読者の皆様にもいろいろ考えていただきたいのです。そのとき、私の考えの進み具合を正直に示すことが大事なことだと思うのです。
この論文を読まれたとき、論文の内容そのものより、皆様自身が自分で考えられるのが重要なのです。
ということで、このままの状態で論文を書き進めて、結論の前に、新しい章でも設けて、そこに、論文執筆中の私の考え方の変化についてまとめようと考えています。
<分からないことを説明できるか? >
これは分からないことを分かるようにする、分からない問題の答えを出す、ということではありません。
私が書いている論文で、問題解決について、全部分かるようになれないのはほぼ確かなのです。どんなに頑張っても分からないことがあるのは仕方ないことだと思っています。問題は、何がどのように分からないかを知ることができるか、そして、それを、読者が分かるように、役に立つように、説明できるか、なのです。
結局、「心の問題」(私の論文「私の問題解決の考え方」第1、2章参照)が解決できない可能性が高いのです(できないとは言いませんが)。暗黙知と言ってもいいかもしれません。人間には説明できないことかもしれません。少なくともギリシャの時代から、頭のいい人達が考えてきたことなのですから。
私は、この論文「私の問題解決の考え方」で、私のやり方や考え方を紹介して、皆様にも、それぞれの立場で考えていただけたらと思っています。
© Rakuten Group, Inc.






