PR
Keyword Search
▼キーワード検索
算太・数子
【算太・数子の算数教室】(R)の楽天ブログです☆ ［算数］を楽しく勉強していきましょう！！
Calendar
まだ登録されていません
Comments
コメントに書き込みはありません。
Freepage List
2012.06.22
カテゴリ： カテゴリ未分類
※───────────────────────────────※
【算数合格トラの巻】
【算太・数子の算数教室】(R)
※───────────────────────────────※
(o^-')b
本日はこの問題にチャレンジ☆
平面図形の［内接円］の問題です♪
※───────────────────────────────※
2012/06/22（金）
(^0^)/ 本日は【平面図形】の問題です♪
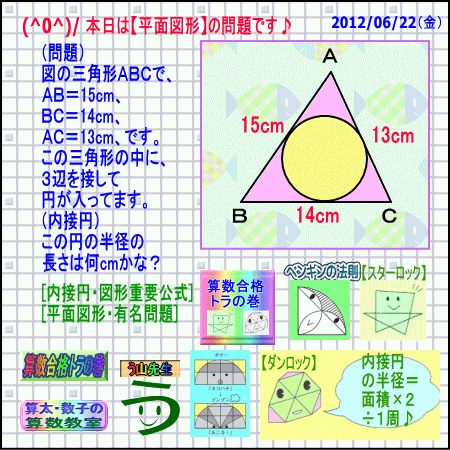
（問題）
図の三角形ＡＢＣで、
ＡＢ＝15cm、
ＢＣ＝14cm、
ＡＣ＝13cm、です。
この三角形の中に、
３辺を接して
（内接円）
この円の半径の
長さは何cmかな？
[内接円・図形重要公式]
※───────────────────────────────※
(*^ー^)ノ
平面図形の重要公式問題、
［内接円の半径］の問題です☆
【ダンロック】君が言ってますように、
『内接円の半径＝
面積×２÷１周♪』
です。
この公式は、
【算数合格トラの巻】のサイトにも
昔から載せていますよね！
中学受験の君も覚えておこう☆（＾0＾）
本日の問題のポイントです☆
（ア）内接円の半径を求める
（イ）三角形の面積を求める
の、二つをクリアしないと解けない問題です。
高校生ではないので、
（イ）三角形の面積を求める
は、【ヘロンの公式】は使いません☆
さて、
【ヘロンの公式】を使わずに、
君は、三角形の面積を求めて、
内接円の半径を求めることが出来るかな♪（＾～＾）
［内接円］を深く理解して、
【平面図形で算数合格】しましょう☆(o^-')b
う山先生の予想正答率は、
正しく正解 → 20％
カンで正解 → 20%
です。
ではレッツ・ゴー！！
☆(^o^)/
答えは、
↓
↓
↓
↓
↓
↓
↓
↓
↓
【答え】［４cm］ です。
(*^ー^)ノ
【内接円の半径】を求める公式はＯＫかな？
【ヘロンの公式】は興味ある人は調べてみよう！
君は本日の問題を（ルート）なんか使わないで、
解けたかな☆(o^-')b
（う山先生の解法は今週の指導にて）
※───────────────────────────────※
中学受験・算数プロ家庭教師・受験算数・算数個人指導
※───────────────────────────────※
□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□
［発行者氏名]
【う山雄一】
［発行者web］
【算数合格トラの巻】
［著作］
【算太・数子の算数教室】(R)
［著作］
【算遊記】
［仕事URL］
http://www2.to/sansu
http://www.alpha-net.ne.jp/users2/popopo/
［仕事用メール］
??????@hotmail.com
［ブログ］
【算数合格トラの巻】
http://ameblo.jp/sansu/
http://blogs.yahoo.co.jp/sansu_gokaku_toranomaki
［ブログ］
【算太・数子の算数教室】(R)
http://ameblo.jp/santa-kazuko/
http://blogs.yahoo.co.jp/santa_kazuko_1994
［ブログ］
【う山先生】
http://uyama.blog85.fc2.com/
http://happy.ap.teacup.com/uyama/
http://blog.livedoor.jp/sansu/
□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□
☆
☆
お気に入りの記事を「いいね！」で応援しよう
Last updated
2012.06.22 10:53:57
【毎日開催】
15記事にいいね！で1ポイント
© Rakuten Group, Inc.
