
สำหรับคนทำงานสาย IT ช่วงหลายปีหลังมานี้น่าจะไม่มีใครไม่เคยได้ยินคำว่าข้อมูลขนาดใหญ่ (big data) แม้หลายคนจะคิดว่าคำดังกล่าวเป็นเพียงแค่คำแฟชั่นเท่ๆ (buzzword) เท่านั้น แต่ก็ปฏิเสธไม่ได้ว่าโลก IT ก้าวมาถึงขั้นที่ให้ความสำคัญกับการขุดหาความรู้ (data mining) จากข้อมูลที่มีอยู่กันซักพักแล้ว
ส่วนก้าวต่อไปในโลก IT คงหนีไม่พ้นเครื่องจักรที่เรียนรู้ได้ (machine learning) และปัญญาประดิษฐ์ (artificial intelligence) การจะเข้าใจในศาสตร์เหล่านี้ได้ แค่เขียนโปรแกรมเป็นอย่างเดียวนั้นไม่เพียงพออีกต่อไป แต่ยังต้องรู้จักและจัดการกับข้อมูลเป็นอีกด้วย
บทความนี้จะพาไปสัมผัสกับภาษา R ที่แม้จะมีรากฐานมาจากการใช้งานทางสถิติ แต่ภายหลังก็ปรับตัวมารองรับการคำนวณข้อมูลที่ซับซ้อนยิ่งขึ้น จนกลายเป็นหนึ่งในภาษาที่มาแรงไม่ควรมองข้าม

ประวัติโดยย่อ
R เป็นภาษาแบบเปิดซอร์ซที่ได้รับแรงบันดาลใจมาจากภาษา S โดยมีจุดประสงค์สำหรับการคำนวณและนำเสนอกราฟิกทางสถิติ มันถูกสร้างและเผยแพร่เป็นครั้งแรกในปี 1993 โดย Ross Ihaka และ Robert Gentleman ปัจจุบันตัวภาษาเดินทางมาถึงรุ่นที่ 3.4 แล้ว
ด้วยความเฉพาะทางของมัน R จึงแตกต่างจาก ภาษาโปรแกรมสำหรับงานทั่วไป (general-purpose programming language) อย่างเช่น C, Python ถึงกระนั้น การจะเรียนรู้ R ก็ไม่จำเป็นต้องทิ้งความรู้จากภาษาอื่นๆ ไปเสียทั้งหมด เพียงแค่ให้ระวังความแตกต่างอันเป็นเอกลักษณ์จากภาษาใหม่นี้ก็พอแล้ว
ซึ่งเอกลักษณ์สำคัญอย่างหนึ่งของภาษา R ก็คือการเป็น ภาษาโปรแกรมเชิงอาเรย์ (array language) ที่เน้นการคำนวณข้อมูลพร้อมกันเป็นกลุ่ม แนวคิดนี้อาจฟังดูแปลกและไกลตัว แต่อันที่จริงแล้วมันอาจเป็นเรื่องใกล้ตัวที่หลายคนเคยผ่านหูผ่านตาจนชินด้วยซ้ำ นั่นก็คือ การคำนวณเซลล์หลายเซลล์ด้วยสูตรเดียวกันบนโปรแกรม Excel นั่นเอง
เริ่มต้นใช้งานผ่าน REPL
สำหรับใครที่คุ้นเคยแต่กับการเขียนภาษาที่ต้องคอมไพล์ก่อน เช่น C, Java จะพบว่าการทดลองคำนวณเล็กน้อยๆ ก่อนการเขียนโปรแกรมจริงนั้นเป็นเรื่องที่ยุ่งยากพอสมควร ในภาษาแบบสคริปต์หลายๆ ภาษาจึงมักมีเครื่องมือคำนวณแบบโต้ตอบที่เรียกว่า REPL (read-eval-print loop) แถมมาให้ โดยเครื่องมือนี้มีหลักการทำงานง่ายๆ 3 ขั้นตอนตามชื่อของมัน คือ อ่านคำสั่ง คำนวณค่าตามคำสั่งนั้นๆ แล้วแสดงผลลัพธ์กลับมาให้ผู้ใช้งานเห็นทันที ก่อนจะวนกลับไปรออ่านคำสั่งถัดไปซ้ำเรื่อยๆ นั่นเอง
เครื่องมือดังกล่าวนอกจากจะช่วยให้ผู้ใช้สามารถเรียนรู้ภาษานั้นๆ ได้อย่างรวดเร็วแล้ว มันยังมีค่าเปรียบได้ดั่งกระดาษทด ที่เราสามารถจดบันทึกแนวคิดต่างๆ พร้อมคำนวณผลลัพธ์ออกมาดูความถูกต้องได้ทันทีทันใดอีกด้วย
เราสามารถทดลองใช้ REPL ของภาษา R ได้ผ่านเว็บ R-Fiddle
หรือ Jupyter
ได้ทันที หรือถ้าใคร ติดตั้งโปรแกรมไว้ในเครื่อง
แล้ว ก็เพียงแค่เปิดโปรแกรม terminal/cmd ขึ้นมา พิมพ์ R
(ใช้ตัวอักษรตัวใหญ่ ต่างจากคำสั่งโดยทั่วไปที่มักใช้ตัวเล็กทั้งหมด) แล้วกดปุ่ม <Enter>
เมื่อเข้ามาแล้วเราจะพบกับข้อความต้อนรับที่บอกรายละเอียดว่ากำลังใช้โปรแกรมเวอร์ชันใด พร้อมทั้งแสดงคำสั่งพื้นฐานสำหรับช่วยเหลืออีกเล็กน้อย เลื่อนลงมาดูที่ด้านล่างสุดของหน้าจอ จะพบกับเครื่องหมาย >
ที่ตามด้วยเคอร์เซอร์กะพริบรอรับคำสั่งที่เราพิมพ์เข้าไป เราอาจทดลองคำนวณการบวกเลขง่ายๆ เช่น 1+1
ได้ดังนี้
> 1+1
[1] 2
สังเกตว่าที่ด้านหน้าของผลลัพธ์ (เลข 2
) จะมีตัวเลขในวงเล็บปีกแข็ง ( [1]
) แสดงอยู่ นี่เป็นตัวเลขที่จะแสดงเฉพาะในโหมด REPL เท่านั้น มันมีไว้เพื่อช่วยให้เรานับได้อย่างสะดวกว่า ค่าผลลัพธ์ที่เห็นเป็นตัวแรกในแถวนี้เป็นผลลัพธ์ตัวที่เท่าไรจากผลลัพธ์ทั้งหมด
เราอาจทดลองคำนวณค่าอื่นๆ ด้วยตัวดำเนินการพื้นฐานทางคณิตศาสตร์ที่เราคุ้นเคยในภาษาทั่วไป อันได้แก่ บวก ( +
) ลบ ( -
) คูณ ( *
) หาร ( /
) หรือบางตัวก็แปลกกว่าภาษาอื่นบ้าง เช่น ยกกำลัง ( ^
) หารเอาเศษ ( %%
) และหารปัดเศษทิ้ง ( %/%
) สังเกตว่า R จะมองว่าตัวเลขต่างๆ เป็นตัวเลขแบบจุดทศนิยมลอยตัว (floating point) โดยปริยาย ดังนั้นการคำนวณตัวเลขแปลกๆ มักจะไม่ส่งผลให้โปรแกรมต้องหยุดทำงานเนื่องจากมีข้อผิดพลาดเกิดขึ้น เช่น
> 1/0
[1] Inf
แต่นั่นก็ไม่ได้หมายความภาษา R จะเป็นภาษาที่เขียนโปรแกรมได้โดยไม่มีข้อผิดพลาดแต่อย่างใด เช่น ข้อผิดพลาดนี้ที่เกิดจากการพิมพ์คำสั่งผิด (syntax error)
> (1+)*3
Error: unexpected ')' in "(1+)"
เมื่อเจอข้อผิดพลาดเหล่านี้ก็ไม่ต้องตกใจ ขอเพียงแค่ค่อยๆ ทำความเข้าใจว่าข้อความดังกล่าวบอกว่าเราผิดพลาดตรงไหน แล้วก็แก้ไขข้อผิดพลาดนั้น โปรแกรมก็จะทำงานต่อไปได้แล้ว
ส่วนในการทำงานจริง เราอาจลืมไปว่าฟังก์ชันที่ต้องการใช้นั้นเรียกใช้งานอย่างไร หรือประเภทข้อมูลที่ใช้มีสมบัติใดบ้าง เราสามารถเรียกเอกสารขึ้นมาอ่านได้ทันทีผ่านฟังก์ชัน help()
(หรือจะใช้ทางลัดเป็นเครื่องหมาย ?
เพียงตัวเดียวนำหน้าหัวข้อที่ต้องการก็ได้)
help() # หน้าแรกเอกสาร
help("+") # เอกสารเกี่ยวกับการดำเนินการตัวเลขพื้นฐาน
help(numeric) # เอกสารเกี่ยวกับข้อมูลประเภทตัวเลข
เมื่อต้องการออกจาก REPL สามารถพิมพ์ฟังก์ชัน q()
จากที่ได้เกริ่นไปข้างต้นว่าการใช้งานโปรแกรม REPL นี้เปรียบได้ดั่งกระดาษทด โปรแกรมจะถามว่าเราต้องการเก็บบันทึกตัวแปรและคำสั่งต่างๆ บนกระดาษทดครั้งนี้ไว้เผื่อใช้ซ้ำในครั้งถัดไปหรือไม่ หากตอบว่าใช่ ( y
) ทุกครั้งนับจากนี้ที่เปิดโปรแกรม REPL จากตำแหน่งแฟ้มเดิมขึ้นมา เราจะสามารถเรียกใช้ตัวแปรที่เคยสร้างและย้อนดูคำสั่งที่เคยเรียกจากครั้งนี้ได้เสมอ
ตัวแปรและประเภทข้อมูล
แม้ภาษา R จะรับแนวคิด การเขียนโปรแกรมเชิงวัตถุ (object-oriented programming) ที่ทำให้เราสามารถดัดแปลงและสร้างประเภทข้อมูลชนิดใหม่ๆ ขึ้นมาได้ แต่โดยส่วนใหญ่เราจะวนเวียนอยู่กับข้อมูลพื้นฐานเพียงไม่กี่ประเภทเท่านั้น
การทดสอบว่าข้อมูลดังกล่าวถูกจัดอยู่ในประเภทใด สามารถใช้ฟังก์ชัน class()
เพื่อตรวจสอบประเภทของข้อมูลนั้นได้ เช่น
> class("hello")
[1] "character"
แต่ก่อนที่เราจะไปดูว่าภาษา R มีประเภทข้อมูลที่น่าสนใจใดบ้าง จะขอกล่าวถึงเรื่องพื้นฐานที่น่าสนใจไม่แพ้กันอย่างการประกาศตัวแปรเสียก่อน
ประกาศตัวแปร
การประกาศตัวแปรในภาษา R จะใช้สัญลักษณ์ที่แตกต่างจากภาษาโปรแกรมโดยทั่วไป แต่ดูคุ้นเคยเมื่อเขียนเป็นสมการคณิตศาสตร์ ซึ่งก็คือสัญลักษณ์ลูกศรซ้าย ( <-
) นั่นเอง ดังเช่นตัวอย่างการประกาศตัวแปรเหล่านี้
> x <- 42
> y <- "We \u2764 R-lang"
อย่างไรก็ตาม R ยังยอมให้ใช้สัญลักษณ์เท่ากับ ( =
) เพื่อประกาศตัวแปรได้เช่นกัน (แม้หลายที่เช่น Google
จะไม่แนะนำวิธีนี้) ความแตกต่างคือสัญลักษณ์เท่ากับถูกออกแบบมาเพื่อใช้ประกาศพารามิเตอร์/อาร์กิวเมนต์ของฟังก์ชันเป็นหลัก การใช้สัญลักษณ์ลูกศรซ้ายเพื่อประกาศพารามิเตอร์/อาร์กิวเมนต์ฟังก์ชันอาจทำให้โปรแกรมทำงานผิดพลาดได้
อนึ่ง R ยังยินยอมให้ใช้สัญลักษณ์จุด .
เป็นส่วนผสมในชื่อตัวแปรได้ สำหรับใครที่คุ้นชินกับภาษาอื่นที่ใช้จุดเพื่อคั่นแอตทรีบิวต์/เมธอด ให้ระวังว่าเมื่อพบตัวแปรมีจุดในภาษา R ไม่ได้หมายความว่าตัวแปรนั้นจะเป็นแอตทรีบิวต์ของวัตถุด้านหน้าจุดแต่อย่างใด
เราสามารถขอดูตัวแปรทั้งหมดที่เราสร้างขึ้นมาได้ผ่านฟังก์ชัน ls()
และทำลายตัวแปร ได้ผ่านฟังก์ชัน rm()
ประเภทข้อมูลเดี่ยว
ข้อมูลเดี่ยวคือข้อมูลขนาดเล็กที่สุดที่ไม่สามารถแบ่งย่อยลงไปได้อีก และไม่สามารถนำไปใช้คำนวณทางสถิติได้
ข้อมูลตัวเลข
เนื่องจาก R เป็นภาษาที่เน้นการนำไปใช้งานทางสถิติเป็นหลัก การเก็บตัวเลขแบบจุดทศนิยมลอยตัว (ในภาษา R เรียกข้อมูลชนิดนี้ว่า numeric
) จึงเป็นท่ามาตรฐานที่ R เลือกใช้ เพราะนำไปคำนวณต่อได้ง่าย อย่างไรก็ตาม R ยังมีข้อมูลตัวเลขอีกสองประเภทให้เลือกใช้เพิ่มเติมตามความเหมาะสมเช่นกัน ซึ่งก็คือ
- จำนวนเต็ม (
integer) สร้างได้โดยเขียนห้อยตัวLไว้ข้างหลังตัวเลข เช่น100Lจำนวนเต็มมีไว้สำหรับใช้ในงานที่ต้องการให้แน่ใจว่าการคำนวณต่างๆ เป็นแบบ วิยุตคณิต (discrete mathematics) หรือใช้เพื่อบ่งบอกจำนวนการวนซ้ำ - จำนวนเชิงซ้อน (
complex) สร้างได้โดยเขียนห้อยตัวiไว้ข้างหลังตัวเลข เช่น1i,3+4iจำนวนเชิงซ้อนมีไว้สำหรับงานทางด้านวิทยาศาสตร์-วิศวกรรมบางแขนง เช่น การคำนวณด้านแม่เหล็กไฟฟ้า พลศาสตร์ของไหล
ลำดับของตัวเลขในภาษา R เรียงจากต่ำไปสูงได้แก่ จำนวนเต็ม จำนวนทศนิยม และจำนวนเชิงซ้อน หากมีการใช้งานตัวเลขคละประเภทกัน R จะแปลงตัวเลขที่อยู่ในชั้นต่ำกว่าขึ้นไปเป็นชั้นที่สูงกว่าเสมอ
ข้อมูลตัวอักษร
ภาษา R ไม่แบ่งแย่งข้อมูลตัวอักษรเป็นหลายระดับ (แบบภาษา C) แต่จะมองว่าตัวอักษรชุดหนึ่งไม่ว่าจะยาวเท่าใดคือหนึ่งข้อความเสมอ (แบบภาษา Python) และเรียกข้อมูลชนิดนี้ว่า character
การประกาศข้อความสามารถใช้ได้ทั้งอัญประกาศเดี่ยว ( '
) หรืออัญประกาศคู่ ( "
) ล้อมรอบข้อความที่ต้องการโดยไม่มีความแตกต่างกันแต่อย่างใด
ข้อมูลตรรกะ
การแสดงข้อมูลตรรกะ ( logical
) ว่าถูกหรือผิด จะใช้คำว่า TRUE
กับ FALSE
ตามลำดับ ไม่สามารถใช้ตัวเลขทดแทนได้ อย่างไรก็ตาม หากต้องการประหยัดเวลาพิมพ์ในส่วนนี้ ก็สามารถป้อนแค่ตัวอักษรตัวแรก ( T
, F
) เข้าไปได้เช่นกัน
R ยังมีข้อมูลตรรกะแบบพิเศษอีกตัวหนึ่งเพิ่มเข้ามา คือ ข้อมูลว่าง ( NA
) ซึ่งจะเกิดขึ้นเมื่อพยายามเข้าถึงข้อมูลในตำแหน่งที่ไม่มีข้อมูล หรือพยายามคำนวณค่าทั้งที่ไม่มีข้อมูลอยู่ หมายเหตุว่า R จะไม่ถือว่าเกิดข้อผิดพลาดขึ้นจนต้องหยุดการคำนวณ แต่อาจขึ้นคำเตือนบางครั้งเมื่อพยายามทำงานบนข้อมูลที่ไม่สมบูรณ์นี้
ประเภทข้อมูลชุด
ข้อมูลชุดคือข้อมูลที่เก็บรวบรวมข้อมูลเดี่ยวหลายๆ ตัวมาไว้ในที่เดียวกัน จึงทำให้สามารถนำไปวิเคราะห์เชิงสถิติต่อได้
เวกเตอร์
อย่างที่หลายคนน่าจะสังเกตเห็นตอนที่ทดลองคำสั่งบน REPL ไปแล้ว ว่าการคำนวณใดๆ ในภาษา R จะมีตัวเลขตำแหน่งกำกับที่ผลลัพธ์เสมอ นั่นหมายความว่า R ให้ความสำคัญกับการคำนวณตัวเลขหลายตัวพร้อมกันเป็นอย่างมาก อันที่จริงแล้วข้อมูลเดี่ยวทุกชนิดที่สร้างขึ้นในภาษา R จะถูกห่อหุ้มด้วยสิ่งที่เรียกว่าเวกเตอร์ ( vector
) ซึ่งเทียบในภาษาอื่นได้ว่าเป็นอาเรย์ที่มีความยาวไม่จำกัด แม้ว่าข้อมูลชุดนั้นจะมีความยาวเพียงแค่หนึ่งหน่วยก็ตาม
การนำเวกเตอร์หลายชุดมารวมกัน จะเป็นการนำเวกเตอร์มาต่อกันเสมอ ซึ่งก็คือจะได้ผลลัพธ์เป็นเวกเตอร์เพียงชุดเดียวที่ไล่สมาชิกจากเวกเตอร์ตัวแรกไปจนจบ แล้วจึงไล่สมาชิกจากเวกเตอร์ตัวถัดไปเรื่อยๆ (ไม่ใช่ได้ผลลัพธ์เป็นเวกเตอร์ซ้อนเวกเตอร์แต่อย่างใด) โดยฟังก์ชันที่ทำหน้าที่ประกาศเวกเตอร์หรือนำเวกเตอร์มาต่อกันคือ c()
ดังตัวอย่างต่อไปนี้
> x <- 1
> y <- c(2,3,4)
> z <- c(x,y)
> z
[1] 1 2 3 4
การถามประเภทข้อมูลของเวกเตอร์ด้วยฟังก์ชัน class()
จะไม่รับคำตอบกลับมาว่ามันคือเวกเตอร์ แต่จะได้รับคำตอบว่าสมาชิกทุกตัวในเวกเตอร์นี้เป็นข้อมูลเดี่ยวประเภทใด นี่ทำให้เมื่อนำเวกเตอร์ของข้อมูลคละชนิดกันมารวมกัน สมาชิกบางตัวจะถูกแปลงประเภทข้อมูลขึ้นไปเป็นแบบที่สามัญกว่าทันที
> class(z)
[1] "numeric"
> mix <- c(1,"a",NA,T)
> mix
[1] "1" "a" NA "TRUE"
> class(mix)
[1] "character"
การเข้าถึงสมาชิกในเวกเตอร์ สามารถใช้สัญลักษณ์วงเล็บปีกแข็งล้อมรอบตัวเลขตำแหน่งที่ต้องการ โดย R จะเริ่มนับสมาชิกตัวแรกด้วยเลขหนึ่ง (one-based indexing) และการเข้าถึงสมาชิกตัวที่สูงเกินกว่าขนาดของเวกเตอร์จะได้ผลลัพธ์เป็นข้อมูลว่าง เช่นนี้
> z[3]
[1] 3
> z[10]
[1] NA
> length(z)
[1] 4
นอกจากนี้ เรายังสามารถเข้าถึงข้อมูลย่อยพร้อมๆ กันหลายตัวได้ โดยส่งเวกเตอร์ของตำแหน่งทั้งหมดที่ต้องการเข้าไป ซึ่งสามารถเขียนย่อช่วงตำแหน่งที่ติดกันโดยใช้สัญลักษณ์โคลอน ( :
) หรือจะส่งเวกเตอร์ตรรกะเพื่อบอกว่าจะเลือกสมาชิกตัวไหนบ้างก็ได้ ตามตัวอย่างต่อไปนี้
> z[c(2,4)]
[1] 2 4
> z[1:3]
[1] 1 2 3
> z[4:2]
[1] 4 3 2
> z[c(T,F,F,T)]
[1] 1 4
> z[c(T,F)]
[1] 1 3
การคำนวณทางคณิตศาสตร์ระหว่างเวกเตอร์ จะเป็นการจับคู่สมาชิกแต่ละตัวในเวกเตอร์แล้วคำนวณตามเครื่องหมายคณิตศาสตร์ที่ให้ไว้ ถ้าเวกเตอร์มีขนาดไม่เท่ากัน เวกเตอร์ตัวที่สั้นกว่าจะถูกนำมาใช้จับคู่ซ้ำเรื่อยๆ นั่นเอง
> z - 1
[1] 0 1 2 3
> z * c(1,-1)
[1] 1 -2 3 -4
> z + c(4,5,6)
[1] 5 7 9 8
Warning message:
In z + c(4, 5, 6) :
longer object length is not a multiple of shorter object length
ข้อมูลชุดสำหรับคำนวณทางคณิตศาสตร์
หากเราต้องการเก็บข้อมูลที่เทียบเท่ากับอาเรย์สองมิติในภาษาอื่น ภาษา R จะเรียกข้อมูลชนิดนั้นว่าเมทริกซ์ ( matrix
) การจะสร้างข้อมูลชนิดนี้ได้ต้องเตรียมข้อมูลให้อยู่ในรูปของเวกเตอร์เสียก่อน แล้วจึงค่อยเปลี่ยนประเภทข้อมูลเป็นเมทริกซ์ ดังนี้
> A <- matrix(z, nrow=2, ncol=2)
[,1] [,2]
[1,] 1 3
[2,] 2 4
> B <- matrix(z, nrow=2, ncol=2, byrow=TRUE)
[,1] [,2]
[1,] 1 2
[2,] 3 4
สังเกตว่าที่ตัวเลขกำกับตำแหน่งผลลัพธ์ จะมีสัญลักษณ์ลูกน้ำ ( ,
) เพิ่มเข้ามาด้วย นั่นบ่งบอกว่าการเข้าถึงสมาชิกในข้อมูลประเภทเมทริกซ์ จะต้องเขียนสัญลักษณ์ลูกน้ำกำกับด้วยเช่นกัน
> A[1,2]
[1] 3
> B[,2]
[1] 2 4
> A[2:1,2:1]
[,1] [,2]
[1,] 4 2
[2,] 3 1
หากเรายังต้องการเก็บอาเรย์ที่มีมิติสูงขึ้นไปกว่านี้ ก็สามารถสร้างประเภทข้อมูลอาเรย์ได้ผ่านฟังก์ชัน array()
โดยระบุขนาดในแต่ละมิติเข้าไป
> array(1:24, c(4,3,2,1))
, , 1, 1
[,1] [,2] [,3]
[1,] 1 5 9
[2,] 2 6 10
[3,] 3 7 11
[4,] 4 8 12
, , 2, 1
[,1] [,2] [,3]
[1,] 13 17 21
[2,] 14 18 22
[3,] 15 19 23
[4,] 16 20 24
สังเกตว่าการดำเนินการทางคณิตศาสตร์โดยใช้เครื่องหมายธรรมดาทั่วไป ( +
, -
, *
, /
) จะเป็นการนำสมาชิกในข้อมูลทั้งสองชุดมาจับคู่กันตัวต่อตัวแล้วดำเนินการทางคณิตศาสตร์แบบธรรมดาเท่านั้น หากต้องการดำเนินการทางคณิตศาสตร์แบบเมทริกซ์ ต้องใช้เครื่องหมายคณิตศาสตร์สำหรับเมทริกซ์โดยเฉพาะ (เช่น การคูณเมทริกซ์ %*%
) ดังตัวอย่างต่อไปนี้
> A * B
[,1] [,2]
[1,] 1 6
[2,] 6 16
> A %*% B
[,1] [,2]
[1,] 10 14
[2,] 14 20
กรอบข้อมูล
กรอบข้อมูล ( data.frame
) คือข้อมูลชุดแบบตารางเช่นเดียวกับตารางในฐานข้อมูล กล่าวคือ แต่ละหลักของตารางจะบอกว่าหลักนี้ใช้เก็บข้อมูลเรื่องใด ส่วนแต่ละแถวของตารางก็คือข้อมูลหนึ่งระเบียน (record) นั่นเอง
วิธีสร้างกรอบข้อมูล เริ่มจากการเตรียมข้อมูลแต่ละหลักด้วยเวกเตอร์ โดยตรวจสอบให้แน่ใจว่าเวกเตอร์ทุกตัวมีความยาวเท่ากัน แล้วจึงนำมารวมกันด้วยฟังก์ชัน data.frame()
ดังนี้
> handle <- c("Sheldon","Leonard","Penny")
> year <- c(1980,1980,1985)
> iq <- c(187,173,NA)
> big.bang <- data.frame(handle, yob=year, iq)
> big.bang
handle yob iq
1 Sheldon 1980 187
2 Leonard 1980 173
3 Penny 1985 NA
เนื่องจากรูปแบบการเก็บข้อมูลนี้ คล้ายคลึงกับการเก็บโดยเมทริกซ์ การเข้าถึงข้อมูลแต่ละแถว สามารถทำได้ในทำนองเดียวกันกับที่ทำบนเมทริกซ์ คือ
> big.bang[3,]
handle yob iq
3 Penny 1985 NA
ส่วนการเข้าถึงข้อมูลแต่ละหลัก สามารถใช้เครื่องหมาย $
แล้วตามด้วยชื่อของเขตข้อมูลที่ต้องการได้เลย ซึ่งก็คือ
> big.bang$yob
[1] 1980 1980 1985
อนึ่ง หากข้อมูลในหลักซ้ายสุดของตารางมีค่าไม่ซ้ำกัน และเราต้องการค้นหาข้อมูลในแถวนั้นโดยใช้ค่าในหลักซ้ายสุดเป็นคำค้น (เทียบได้กับกุญแจหลักในฐานข้อมูล) ตอนสร้างกรอบข้อมูลให้กำหนดอาร์กิวเมนต์เพิ่มเข้าไปเล็กน้อย ดังนี้
> new.big.bang <- data.frame(row.names=handle, yob=year, iq)
> new.big.bang
yob iq
Sheldon 1980 187
Leonard 1980 173
Penny 1985 NA
> new.big.bang["Sheldon",]
yob iq
Sheldon 1980 187
นอกจากนี้ อย่าลืมว่าเราสามารถใช้เวกเตอร์ตรรกะซึ่งอาจได้มาจากการคำนวณ เพื่อกรองว่าต้องการใช้ข้อมูลแถวได้บ้างในกรอบข้อมูลนี้ ดังที่จะเห็นได้จากตัวอย่างถัดไป
> use <- new.big.bang$yob == 1980
> use
[1] TRUE TRUE FALSE
> new.big.bang[use,]
yob iq
Sheldon 1980 187
Leonard 1980 173
สถิติและความน่าจะเป็นอย่างรวบรัด
พูดอย่างหยาบๆ แล้ว สถิติคือวิชาที่เล่นกับข้อมูลจำนวนมาก ส่วนความน่าจะเป็นนั้นนำค่าทางสถิติคาดมาเดาอนาคต หลายต่อหลายครั้งสถิติและความน่าจะเป็นมักมาพร้อมกับการสุ่ม เช่น เมื่อเราเจอเหรียญที่ไม่สมดุลเหรียญหนึ่งจึงทดลองโยนดูค่า 100 ครั้ง พบว่าออกหัวถึง 80 ครั้ง เราอาจทำนายได้ว่าเมื่อโยนครั้งต่อไปควรคาดหวังว่าผลลัพธ์จะออกด้านหัวมากกว่าก้อย
สิ่งสำคัญที่เรียกได้ว่าเป็นพระเอกของงานนี้ก็คือ "ข้อมูล" นั่นเอง หากขาดซึ่งข้อมูลแล้ว ไม่ว่าจะสร้างโมเดลทำนายความน่าจะเป็นมาดีขนาดไหนก็คงไร้ประโยชน์
ในหัวข้อนี้ เราอาจสร้างข้อมูลอย่างสุ่มขึ้นมาเพื่อทดลองหาค่าทางสถิติก่อนก็ได้ แต่จะขอแสดงวิธีนำเข้าข้อมูลจากภายนอก ซึ่งแม้บางขั้นตอนจะซับซ้อนอยู่บ้าง แต่ก็ดีกว่าค่อยๆ ป้อนตัวเลขเข้าไปทีละตัวเป็นแน่แท้
นำเข้าข้อมูล
เนื่องจากการเข้าถึงไฟล์ข้อมูลทางสถิติต่างๆ ของประเทศไทยยังเป็นไปได้ยาก ตัวอย่างต่อไปนี้จะขอยืมข้อมูลจากต่างประเทศมาใช้ก่อน ซึ่งก็คือข้อมูลคะแนนเฉลี่ยของการสอบ SAT จากโรงเรียนระดับมัธยมในเมืองนิวยอร์ก (แนวคิดข้อสอบเทียบได้กับการสอบแอดมิชชั่นของไทย) โดยมีขั้นตอนดังนี้
เริ่มจากเข้าไป ดาวน์โหลดข้อมูลดังกล่าวผ่าน Data.gov เลือกรูปแบบไฟล์ที่จะดาวน์โหลดเป็นแบบ CSV (comma separated values) เพื่อความสะดวกในการนำไปใช้ต่อ
เมื่อดาวน์โหลดไฟล์ดังกล่าวเสร็จสิ้น อาจทดสอบความถูกต้องของข้อมูลด้วยการเปิดไฟล์ดังกล่าวผ่านโปรแกรมจำพวกสเปรดชีต เช่น Microsoft Excel, Google Sheets, LibreOffice Calc หรือจะเปิดผ่านโปรแกรมแก้ไขข้อความทั่วไปก็ได้
ต่อไปจะอ่านข้อมูลเข้ามาใช้ใน R โดยคร่าวๆ แล้วสามารถทำได้ดังนี้ (สำหรับ Windows ใช้เครื่องหมาย /
เพื่อคั่นระหว่างโฟลเดอร์เช่นเดียวกัน)
> data <- read.csv("PATH/TO/DOWNLOAD/SAT_Results.csv")
อย่างไรก็ตาม หากเราลองดูข้อมูลตัวเลขที่อ่านเข้ามา จะพบว่าในหลักเดียวกันนั้น บางแถวก็ยังมีตัวอักษร "s"
ปนอยู่ด้วย หากยังพอจำกันได้ การมีข้อมูลตัวอักษรปนกับข้อมูลตัวเลขนั้น จะทำให้ข้อมูลตัวเลขถูกแปลงไปเป็นตัวอักษรทันที ซึ่งอาจส่งผลให้วิเคราะห์ผิดพลาดในภายหลัง นี่เป็นสิ่งที่เราสามารถหลีกเลี่ยงได้โดยระบุว่าตัวอักษร "s"
หมายถึงข้อมูลในช่องนั้นหายไป (ข้อมูลชุดอื่นๆ อาจใช้ตัวอักษรระบุค่าที่หายไปแตกต่างกัน เช่น "-"
, "n/a"
เป็นต้น)
> data <- read.csv("PATH/TO/DOWNLOAD/SAT_Results.csv",
na.strings="s")
นอกจากนี้แล้ว เรายังสามารถระบุเพิ่มเติมว่า ให้ใช้หลักแรกสุดเป็นกุญแจในการเข้าถึงข้อมูลในแถวนั้นๆ โดยเพิ่มอาร์กิวเมนต์ row.names
เข้าไป
> data <- read.csv("PATH/TO/DOWNLOAD/SAT_Results.csv",
na.strings="s", row.names=1)
สำหรับข้อมูลชุดนี้ การระบุอาร์กิวเมนต์ตามข้างต้นก็ถือว่าเพียงพอแล้ว เพราะเมื่อไม่สนใจค่า NA
ทั้งหมดที่พบ R จะพยายามแปลงข้อมูลแต่ละแถวให้เป็นตัวเลข เพื่อให้นำไปใช้งานต่อในเชิงสถิติได้ทันที อย่างไรก็ตาม หากเราไม่มั่นใจว่า R จะแปลงประเภทข้อมูลได้ถูกต้อง เรายังสามารถบังคับประเภทของตัวแปรในแต่ละแถวได้เช่นกัน
> data <- read.csv("PATH/TO/DOWNLOAD/SAT_Results.csv",
na.strings="s", row.names=1,
colClasses=c(rep("character",2), rep("numeric",4)))
ท้ายสุด เราอาจเลือกลบแถวที่ข้อมูลขาดหาย (มีข้อมูลเป็น NA
) ทิ้งไป เพื่อความสะดวกในการคำนวณข้อมูลในภายหลัง ซึ่งทำได้โดย
> data <- na.omit(data)
ภาพรวมข้อมูลทางสถิติ
เมื่อต้องการเริ่มวิเคราะห์ข้อมูลชุดหนึ่งๆ การไล่ค่าทุกค่าในข้อมูลชุดนั้นออกมาแล้วทำความเข้าใจกับมันมักเป็นการกระทำที่เสียเวลาและไม่สมเหตุสมผล วิธีการที่มีประสิทธิภาพกว่าคือการดูข้อสรุปชิ้นเล็กๆ ที่ถูกสรุปออกมาจากข้อมูลชุดนั้น โดยหลักๆ แล้วเราอาจสนใจค่าสรุปอยู่ 2 แบบ ได้แก่ ตำแหน่งข้อมูล และการกระจายข้อมูล
ตำแหน่งข้อมูล
ตำแหน่งข้อมูลจะแสดงว่าข้อมูลดังกล่าวมีตำแหน่งสำคัญๆ ตรงไหนบ้าง เช่น ค่ามากสุด/น้อยสุด ค่ากลางข้อมูล และควอร์ไทล์
ค่ากลางข้อมูลคือค่าที่แสดงว่าข้อมูลชุดนั้นมีค่าลู่เข้าสู่ตรงกลางที่เท่าใด ซึ่งอาจแบ่งย่อยได้เป็นอีก 3 ประเภท คือ
- มัชฌิม (mean) หรือบางที่ก็เรียกว่าค่าเฉลี่ย (average) หาได้จากการนำทุกค่าในข้อมูลมาบวกรวมกัน แล้วจึงหารด้วยจำนวนข้อมูลที่ใช้
- มัธยฐาน (median) หาได้จากการเรียงข้อมูลจากน้อยไปมากตามลำดับ แล้วดูว่าที่ตำแหน่งตรงกลางของข้อมูลมีค่าเป็นเท่าใด
- ฐานนิยม (mode) หาได้จากการนับว่าค่าใดปรากฏซ้ำมากที่สุดในข้อมูล
ค่าทั้งสามนี้ไม่จำเป็นต้องมีค่าเท่ากัน ซึ่งก็ถือเป็นเรื่องปรกติเนื่องจากข้อมูลมักมีการกระจายตัวไม่สม่ำเสมอ
ส่วน ควอร์ไทล์ จะใช้แนวคิดเดียวกันกับการหามัธยฐาน เพียงแต่แบ่งข้อมูลออกเป็นกลุ่มที่มีขนาดเท่ากันเพิ่มเป็น 4 กลุ่ม และสนใจค่าที่อยู่ตรงจุดเปลี่ยนระหว่างแต่ละกลุ่ม ดังนี้
- ควอร์ไทล์ที่ 1 (1st quartile) คือค่าที่มีตำแหน่งอยู่ตรงกลางระหว่างค่าน้อยสุดและค่ามัธยฐาน
- ควอร์ไทล์ที่ 2 (2nd quartile) คือมัธยฐานนั่นเอง (และเรามักไม่ค่อยเรียกว่า "ควอร์ไทล์ที่ 2" เท่าใดนักเพราะสามารถเรียกชื่อที่พื้นฐานกว่าได้)
- ควอร์ไทล์ที่ 3 (3rd quartile) คือค่าที่มีตำแหน่งอยู่ตรงกลางระหว่างค่ามากที่สุดและค่ามัธยฐาน
ใน R เราสามารถเรียกฟังก์ชัน summary()
เพื่อดูภาพรวมตำแหน่งข้อมูลต่างๆ เหล่านี้ได้ทันที เช่น
> summary(data$SAT.Math.Avg..Score)
Min. 1st Qu. Median Mean 3rd Qu. Max.
312.0 371.0 395.0 413.4 437.0 735.0
สังเกตว่าผลลัพธ์ดังกล่าว ไม่ได้นำข้อมูลฐานนิยมมาแสดงด้วย เพราะโดยทั่วไปข้อมูลมักมีความแม่นยำของตำแหน่งทศนิยมสูงจนไม่มีข้อมูลชิ้นใดซ้ำกัน การหาฐานนิยมด้วยวิธีพื้นฐานมักไม่ให้ข้อสรุปที่เกิดประโยชน์เท่าไร
เราอาจเลี่ยงไปหาฐานนิยมด้วยการแบ่งข้อมูลเป็นช่วงๆ ผ่านฮิสโตแกรม ซึ่งจะกล่าวถึงในหัวข้อถัดไป
การกระจายข้อมูล
ข้อสรุปเดี่ยวๆ จากการวัดตำแหน่งตัวแทนข้อมูล อาจพอบอกแนวโน้มของข้อมูลส่วนใหญ่ได้บ้าง แต่สิ่งที่มันบอกไม่ได้เลยคือลักษณะการกระจายตัวของข้อมูล ลองพิจารณาตัวอย่างว่ามีร้านค้าอยู่สองร้าน ร้านทั้งสองมีจำนวนลูกค้าเข้าร้านเท่าๆ กันและมีรายได้จากการขายของใกล้เคียงกัน ดังนั้นร้านทั้งสองจึงขายของได้เฉลี่ยต่อลูกค้าเป็นจำนวนเงินไม่แตกต่างกันเท่าใดนัก มองผ่านๆ เราอาจคิดว่าร้านทั้งสองขายสินค้าคล้ายกันและตั้งราคาไม่หนีกัน แต่อันที่จริงแล้วข้อมูลเพียงเท่านี้ไม่สามารถบอกลักษณะความหลากหลายในช่วงราคาที่ลูกค้าจับจ่ายได้เลย เพราะร้านหนึ่งอาจขายของเฉพาะทางไม่กี่อย่างในช่วงราคาแคบๆ ส่วนอีกร้านอาจขายตั้งแต่สากกะเบือยันเรือดำน้ำก็เป็นได้
แต่การวัดตำแหน่งข้อมูลก็ไม่ได้ไร้ประโยชน์เสียทีเดียว เพราะเมื่อนำเอาข้อสรุปหลายๆ ชิ้นมารวมกัน ก็อาจพอบอกถึงการกระจายข้อมูลได้บ้าง เช่น
- พิสัย (range) บอกถึงขนาดของช่วงที่เล็กที่สุดที่สามารถครอบคลุมข้อมูลได้ทั้งหมด คำนวณจากการนำค่ามากที่สุดลบน้อยที่สุดได้เลย
- พิสัยระหว่างควอร์ไทล์ (interquartile range) คำนวณจากการนำค่าของควอร์ไทล์ที่ 3 ลบด้วยค่าของควอร์ไทล์ที่ 1 หรือกล่าวอีกนัยหนึ่งได้ว่า วิธีนี้คือเป็นหาพิสัยที่ครอบคลุมข้อมูลจำนวนครึ่งหนึ่งที่กระจายรอบมัธยฐานนั่นเอง
นอกจากนี้ ยังมีการวัดการกระจายข้อมูลอีกวิธีหนึ่งที่เป็นที่นิยม ซึ่งก็คือ ส่วนเบี่ยงเบนมาตรฐาน (standard deviation, สัญลักษณ์ σ) จุดเด่นของวิธีนี้คือการใช้ข้อมูลทุกตัวมาคำนวณ แทนที่จะอ้างอิงจากค่าสรุปทางสถิติเพียงไม่กี่ค่า (ขอละการอธิบายสมการเนื่องจากมีรายละเอียดค่อนข้างมาก) การวัดการกระจายด้วยวิธีนี้จะใช้ได้ผลดีที่สุดเมื่อข้อมูลมีรูปร่างเป็น การแจกแจงปรกติ (normal distribution) ซึ่งบอกเป็นนัยว่ามีข้อมูลที่อยู่ห่างจากค่าเฉลี่ยไม่เกิน ±1σ อยู่ถึง 68% อย่างไรก็ตาม ข้อมูลที่มีการแจกแจงรูปแบบอื่นจะไม่สามารถสรุปขนาดของการแจกแจงเช่นนี้ได้
ฟังก์ชันสำหรับคำนวณการกระจายข้อมูลในภาษา R ได้แก่
> range(data$SAT.Math.Avg..Score)
[1] 312 735
> IQR(data$SAT.Math.Avg..Score)
[1] 66
> sd(data$SAT.Math.Avg..Score)
[1] 64.68466
พล็อตข้อมูล
จุดแข็งสำคัญของภาษาที่เน้นการใช้งานเชิงสถิติอย่าง R คงหนีไม่พ้นความเรียบง่ายแต่ก็ทรงพลังในการพล็อตข้อมูลขึ้นมาดู ยิ่งเมื่อคำนึงว่ามนุษย์เราสามารถรับรู้รูปทรงได้รวดเร็วกว่าการดูตัวเลขเป็นจำนวนมหาศาลแล้ว การพล็อตข้อมูลนอกจากจะช่วยให้เห็นภาพว่าข้อมูลโดยรวมมีหน้าตาเป็นยังไงแล้ว มันยังช่วยให้เราไม่เข้าใจข้อมูลผิดไปเพียงเพราะเลือกดูแค่ค่าเฉลี่ยที่สรุปมาจากข้อมูลทั้งหมดเท่านั้น ดังเช่นทวีตต่อไปนี้ที่แสดงให้เห็นว่าข้อมูลจริงสามารถแตกต่างกันได้มากแม้จะมีข้อสรุปทางสถิติไม่ต่างกัน
New #chi2017 paper is up. Don't trust statistics alone, visualize your data! https://t.co/amnbAYvsq1 pic.twitter.com/1s6vkge6dl
— Justin Matejka (@JustinMatejka) May 1, 2017
เพื่อความรวดเร็วและถูกต้องของข้อมูล ในหัวข้อนี้เราจะใช้ข้อมูลตัวอย่างที่ภาษา R แถมมา สำหรับสร้างภาพการพล็อตทั้งหมด
พล็อตประชันทุกเขตข้อมูล
เมื่อเราเริ่มทำงานกับข้อมูลชุดใหม่ที่ยังไม่เคยเห็นภาพมาก่อน เราอาจไม่รู้เลยว่าความสัมพันธ์ของแต่ละเขตข้อมูลเป็นอย่างไรบ้าง ดังนั้นสิ่งที่เราควรเริ่มทำเป็นอย่างแรก คือการมองภาพความสัมพันธ์ทั้งหมดอย่างหยาบๆ ก่อน
การพล็อตประชันทุกเขตข้อมูล คือการจับเอาข้อมูลทุกๆ คู่ในแต่ละหลักของกรอบข้อมูลมาประชันกัน แล้วพล็อตแต่ละคู่ของข้อมูลแบบกระจาย (scatter plot) การพล็อตนี้สามารถทำได้ผ่านฟังก์ชันง่ายๆ คือ plot()
ตัวอย่างต่อไปนี้จะยืม ข้อมูลดอกไอริสของ Edgar Anderson
มาใช้ โดยข้อมูลดังกล่าวสามารถเรียกใช้งานได้ทันทีเลยในภาษา R โดยไม่ต้องโหลดไลบรารีใดเพิ่ม
> iris
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
2 4.9 3.0 1.4 0.2 setosa
...
150 5.9 3.0 5.1 1.8 virginica
> plot(iris)
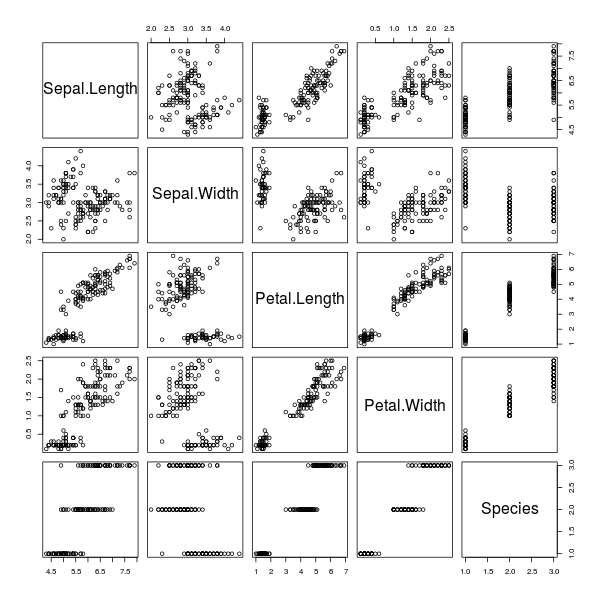
ภาพที่ 1: พล็อตประชันทุกเขตข้อมูลของข้อมูลดอกไอริส
พล็อตกระจาย (Scatter Plot)
จากภาพที่ 1 เราอาจเริ่มต้นให้ความสนใจที่ความยาวกลีบดอก ( Petal.Length
) ต่อความกว้างกลีบดอก ( Petal.Width
) เนื่องจากเมื่อดูอย่างหยาบๆ แล้วน่าจะสร้างโมเดลได้ง่ายที่สุด เราจะเลือกพล็อตกระจายโดยใช้เขตข้อมูลเพียง 2 เขตนี้เท่านั้น เพื่อความสะดวกเราจะบอก R ก่อนว่ากำลังใช้ข้อมูลชุดใดเป็นหลักผ่านฟังก์ชัน attach()
แล้วจึงสั่งพล็อตแบบเฉพาะเจาะจงด้วยสมการดังนี้
> attach(iris)
> plot(Petal.Width ~ Petal.Length)
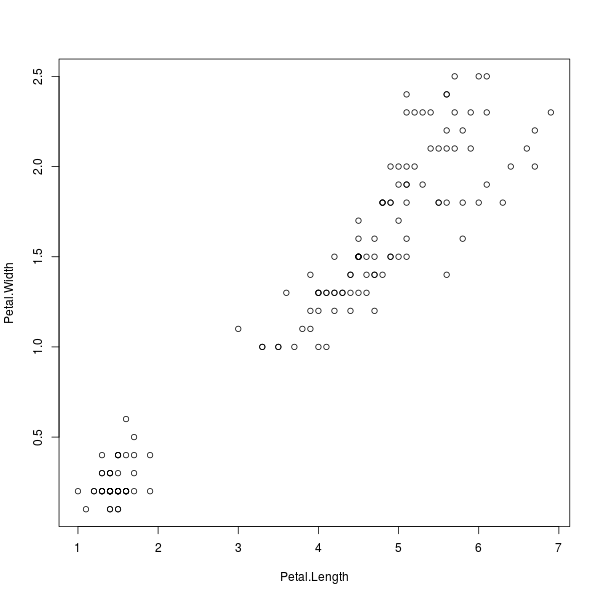
ภาพที่ 2: พล็อตกระจายข้อมูลดอกไอริส โดยสนใจความกว้างต่อความยาวกลีบดอก
หมายเหตุว่า Petal.Width ~ Petal.Length
ไม่ใช่การนำตัวแปรสองตัวมาดำเนินการกันแต่อย่างใด แต่มันคือการประกาศตัวแปรแบบสมการในภาษา R ที่มีความมหัศจรรย์ตรงที่ไม่ต้องใช้เครื่องหมายอัญประกาศมาครอบเพื่อบอกขอบเขตของสมการเฉกเช่นการประกาศข้อความ
อนึ่ง ในอนาคตเมื่อไม่ต้องการใช้ข้อมูลชุดนี้แล้ว (เช่น หลังจบหัวข้อนี้) ควรเรียกฟังก์ชัน detach()
ในทำนองเดียวกันกับที่เรียก attach()
ทุกครั้ง เพื่อไม่ให้เกิดความสับสนจากการที่มีข้อมูลจำนวนหลายชุดมากเกินกว่าที่ต้องการใช้งาน และเพื่อป้องกันกรณีที่มีข้อมูลต่างชุดกันแต่ใช้ชื่อเขตข้อมูลซ้ำกัน
ลากโมเดลเชิงเส้น
จากภาพที่ 2 เราอาจต้องการหาโมเดลเชิงเส้นของข้อมูลดังกล่าว เพื่อทำนายแนวโน้มว่าหากมีข้อมูลใหม่ๆ เพิ่มขึ้นมา ควรคาดหวังว่าข้อมูลเหล่านั้นจะเกิดบริเวณไหน การคำนวณดังกล่าวสามารถทำได้ผ่านฟังก์ชัน lm()
ดังนี้
> lm(Petal.Width ~ Petal.Length)
Call:
lm(formula = Petal.Width ~ Petal.Length, data = iris)
Coefficients:
(Intercept) Petal.Length
-0.3631 0.4158
หากต้องการลากเส้นดังกล่าวลงไปบนพล็อต ขอให้แน่ใจก่อนว่ามีภาพของพล็อตเดิมอยู่ก่อนแล้ว หลังจากนั้นจึงค่อยเรียกฟังก์ชัน abline()
เพื่อลากเส้นตรงจากสัมประสิทธิ์ที่คำนวณได้ ดังนี้
> plot(Petal.Width ~ Petal.Length)
> abline(lm(Petal.Width ~ Petal.Length))
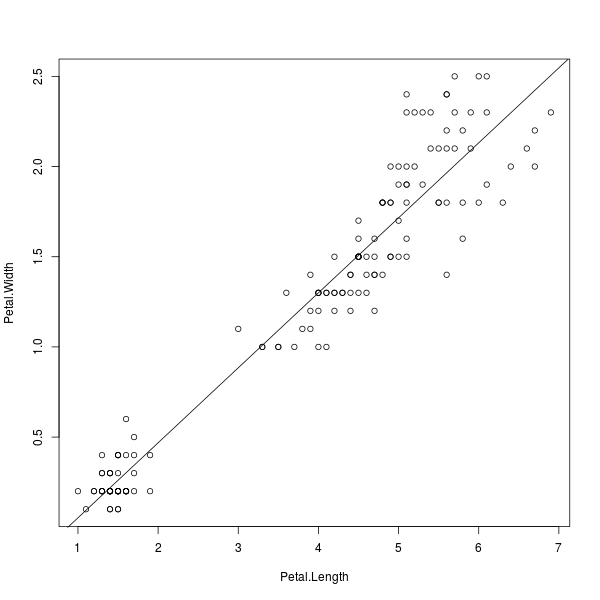
ภาพที่ 3: โมเดลเชิงเส้นของความกว้างต่อความยาวกลีบดอก
ลากโมเดลไม่เชิงเส้น
อย่างไรก็ตาม หากข้อมูลที่สนใจมีแนวโน้มว่าจะไม่เป็นเชิงเส้น ภาษา R ก็มีวิธีการคำนวณโมเดลแบบต่างๆ ให้เลือกใช้ได้หลายวิธี สำหรับวิธีที่ง่ายต่อการเรียกใช้งานที่สุด คือ การประมาณค่าถดถอยแบบท้องถิ่น (local regression หรือ LOESS) ซึ่งจะสร้างโมเดลสมการพหุนามโดยอาศัยข้อมูลแต่ละส่วนในบริเวณใกล้เคียงมาปรับค่า เราสามารถเรียกดูผลลัพธ์จุดตัดต่างๆ บนเส้นโค้งของโมเดลที่คำนวณได้ดังนี้
> loess.smooth(Petal.Length, Petal.Width)
$x
[1] 1.000000 1.120408 1.240816 1.361224 1.481633
...
$y
[1] 0.06892099 0.11545407 0.16200259 0.20869061 0.25544166
...
ส่วนการพล็อตเส้นโค้งดังกล่าว จะเปลี่ยนมาเรียกผ่านฟังก์ชัน lines()
ที่จะลากเส้นตรงเชื่อมระหว่างจุดตัดต่างๆ ตามที่ระบุ แต่เนื่องจากเรามีจุดตัดที่คำนวณไว้เป็นจำนวนมาก จึงได้ผลลัพธ์ออกมาเปรียบเสมือนเส้นโค้งนั่นเอง
> plot(Petal.Width ~ Petal.Length)
> lines(loess.smooth(Petal.Length, Petal.Width))
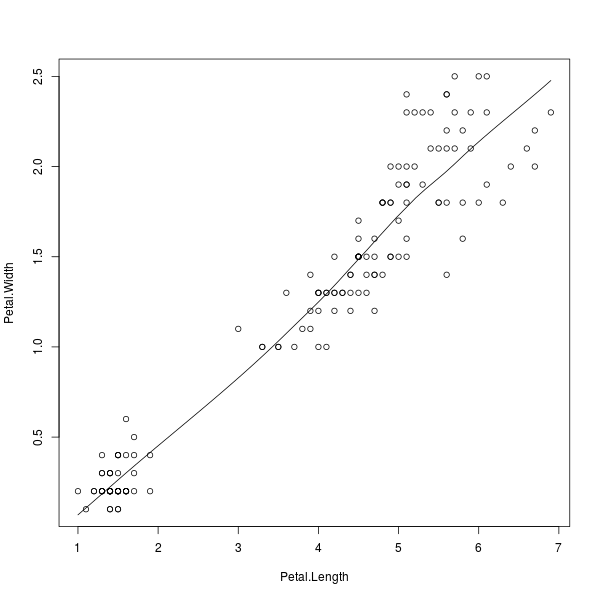
ภาพที่ 4: โมเดลไม่เชิงเส้นของความกว้างต่อความยาวกลีบดอก
ขอให้สังเกตการสลับที่ของตัวแปร สำหรับบรรทัดบนที่ระบุสมการผ่านเครื่องหมาย ~
นั้น จะมีความหมายว่าฝั่งซ้ายของ ~
คือข้อมูลในแกนตั้ง หรืออาจมองเป็นสมการคณิตศาสตร์ที่คุ้นตาโดยเปลี่ยนเครื่องหมาย ~
เป็น =
ในทำนองเดียวกันกับ y=x
นั่นเอง ส่วนในบรรทัดล่างเนื่องจากเราไม่สามารถระบุสมการด้วยเครื่องหมาย ~
ได้ จึงต้องส่งค่าเข้าไปเป็นข้อมูลในแกนนอน ( x
) แล้วจึงตามด้วยแกนตั้ง ( y
) ตามลำดับ
ลากโมเดลอิสระจากสมการที่กำหนดเอง
หากว่าเรายังไม่พอใจกับโมเดลแบบต่างๆ ที่ภาษา R มีให้เลือก เราอาจคำนวณหาสมการด้วยตนเองแล้วนำไปพล็อตทดสอบกับข้อมูลจริงได้ดังนี้
> plot(Petal.Width ~ Petal.Length)
> curve(exp(x-4/3*pi), add=TRUE)
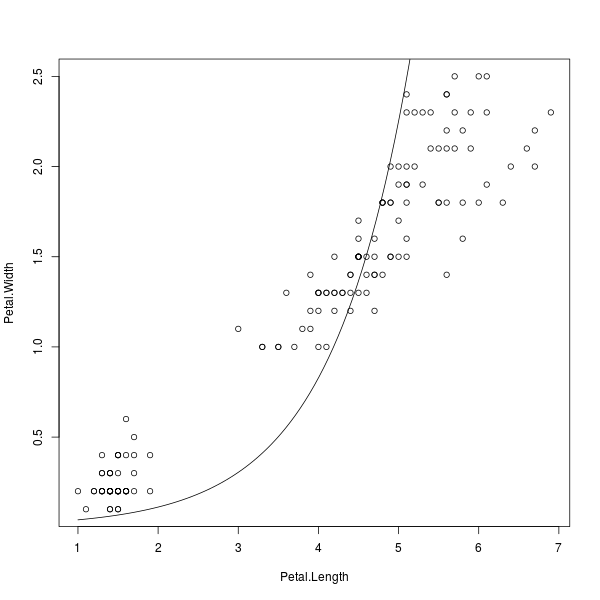
ภาพที่ 5: โมเดลจากสมการ e x-(4/3)π
จุดที่น่าสนใจคือเราสามารถเขียนสมการที่ประกอบขึ้นมาจากพจน์ x
แล้วส่งเป็นอาร์กิวเมนต์แรกของฟังก์ชัน curve()
ได้ตรงๆ โดยที่เราไม่จำเป็นต้องมีตัวแปร x
มาก่อน (หรือหากมีตัวแปรนี้อยู่ มันจะไม่ถูกใช้ในการคำนวณนี้แต่อย่างใด) นี่เป็นอีกหนึ่งในความมหัศจรรย์ของภาษา R ที่พยายามเอาใจผู้ใช้ที่มีพื้นฐานมาจากฝั่งคณิตศาสตร์/สถิติ ซึ่งอาจจะดูผิดปรกติไปบ้างเมื่อเทียบกับภาษาคอมพิวเตอร์อื่นๆ
แต้มสีแยกกลุ่มข้อมูล
อนึ่ง จากข้อมูลตั้งต้นของดอกไอริส นอกจากจะมีข้อมูลเชิงตัวเลขที่บ่งบอกลักษณะดอกไม้แล้ว ยังมีข้อมูลการแบ่งกลุ่มดอกไม้ตามสปีชีส์อีกด้วย ซึ่งข้อมูลการแบ่งกลุ่มนี้อาจไม่เหมาะสมในการพล็อตเทียบกับข้อมูลตัวเลขซักเท่าไร (ดังจะเห็นได้จากแถวล่างสุด/แถบขวาสุดในภาพที่ 1) แต่จะเหมาะสมกว่าหากพล็อตข้อมูลตัวเลขเทียบกันเช่นเดิม แล้วเพิ่มการแบ่งกลุ่มเข้าไปเป็นอีกแกนหนึ่ง เช่น แต้มสีจุดของแต่ละกลุ่มให้แตกต่างกัน ซึ่งสามารถสั่งได้ดังนี้
> plot(Petal.Width ~ Petal.Length, col=Species)
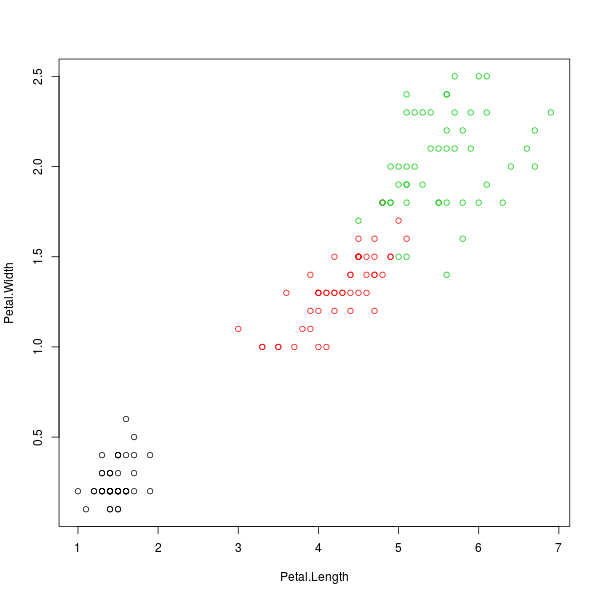
ภาพที่ 6: ข้อมูลดอกไอริสโดยแยกสีตามสปีชีส์
ทั้งนี้ทั้งนั้น หากข้อมูลตั้งต้นไม่ได้ถูกแบ่งกลุ่มไว้ก่อน แต่เรายังต้องการจัดกลุ่มข้อมูลอยู่ อาจเลือกใช้วิธี k-means ในการแบ่งกลุ่มข้อมูล โดยมีหลักการคร่าวๆ ดังนี้
- สุ่มเลือกจุดศูนย์กลางของแต่ละกลุ่มมาทั้งหมด k จุด
- กำหนดว่าจุดข้อมูลต่างๆ อยู่ในกลุ่มใด โดยพิจารณาจากจุดข้อมูลนั้นอยู่ใกล้จุดศูนย์กลางใดมากที่สุด
- คำนวณย้ายค่าจุดศูนย์กลางของแต่ละกลุ่มให้เป็นค่าเฉลี่ยของทุกจุดข้อมูลในกลุ่ม
- ทำซ้ำขั้นตอนที่ 2-3 จนกว่าการจัดกลุ่มจะเสถียร
เนื่องจาก R เตรียมฟังก์ชันดังกล่าวไว้ให้แล้ว วิธีเรียกใช้จึงไม่ยุ่งยากอะไร ขอเพียงแค่เตรียมข้อมูลสำหรับการจัดกลุ่ม และจำนวนกลุ่มที่ต้องการจัดไว้ให้เรียบร้อย แล้วจึงป้อนคำสั่งเหล่านี้ลงไป
> group <- kmeans(iris[3:4], 3)
> plot(Petal.Width ~ Petal.Length, col=group$cluster)
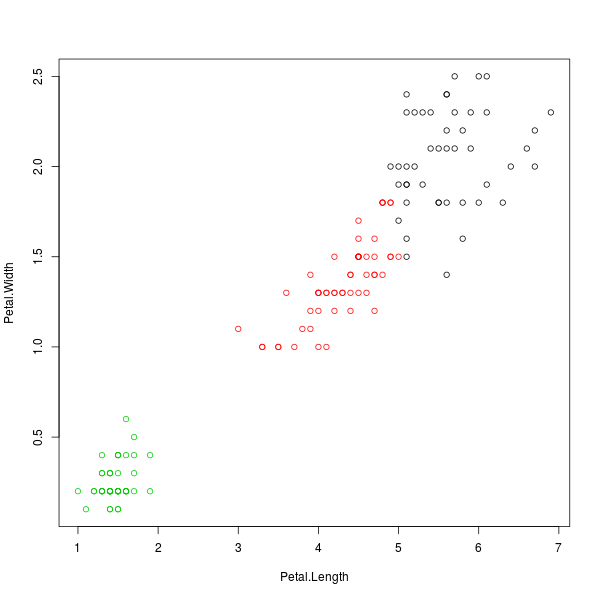
ภาพที่ 7: ข้อมูลดอกไอริสที่จัดกลุ่มแยกสีด้วยวิธี k-means เป็นจำนวน 3 กลุ่ม
หมายเหตุ เนื่องจากอัลกอริทึม k-means เริ่มต้นด้วยการสุ่ม อีกทั้งข้อมูลบางชุดก็ไม่สามารถแบ่งกลุ่มได้อย่างชัดเจน การแบ่งกลุ่มแต่ละครั้งด้วยวิธีดังกล่าวอาจให้ผลลัพธ์ที่แตกต่างกัน
พล็อตข้อสรุปการแจกแจงข้อมูล
เราได้เห็นการพล็อตกระจายที่พล็อตทุกๆ จุดจากข้อมูลที่มีไปแล้ว แต่บางครั้งเราก็ต้องการพล็อตแค่ภาพรวมของข้อมูลเท่านั้น วิธีการพล็อตที่ตอบโจทย์ดังกล่าวและเป็นที่นิยม คือ ฮิสโตแกรมและพล็อตกล่อง
ฮิสโตแกรม (histogram)
ฮิสโตแกรมเป็นหนึ่งในวิธีพื้นฐานสำหรับแสดงการแจกแจงข้อมูล โดยมันจะแสดงแท่งสี่เหลี่ยมที่ความสูงต่างกัน แต่ละแท่งบอกว่ามีข้อมูลจำนวนเท่าใดที่เกิดขึ้นในช่วงนั้นๆ
> hist(Sepal.Width)
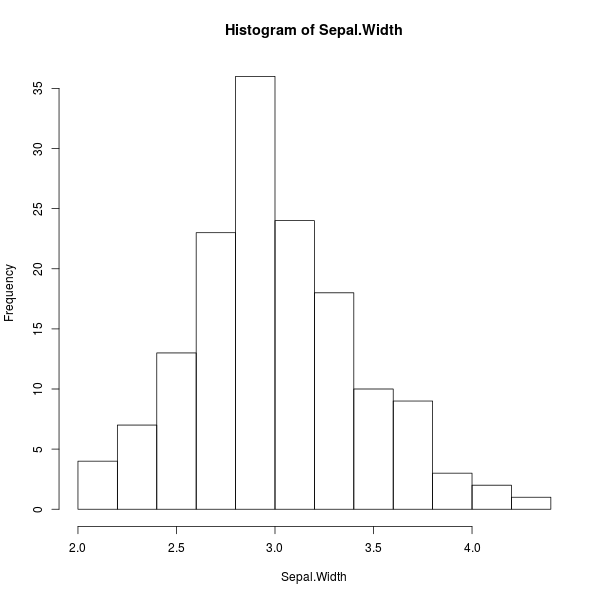
ภาพที่ 8: ฮิสโตแกรมความกว้างกลีบเลี้ยงดอกไอริส
จากภาพที่ 8 จะเห็นว่าแท่งที่สูงที่สุดคือแท่งที่ 5 จากทางซ้าย หรือเมื่อดูเป็นช่วงจะได้ว่าคือช่วงที่ข้อมูลมีค่ามากกว่า 2.8 แต่ไม่เกิน 3.0 ซึ่งจะได้ว่าช่วงนี้คือฐานนิยมนั่นเอง
เราสามารถเปลี่ยนจำนวน รอยต่อระหว่างช่วง
ที่ต้องการได้ ด้วยการระบุอาร์กิวเมนต์ breaks
เพิ่มเข้าไปดังนี้
> hist(Sepal.Width, breaks=4)
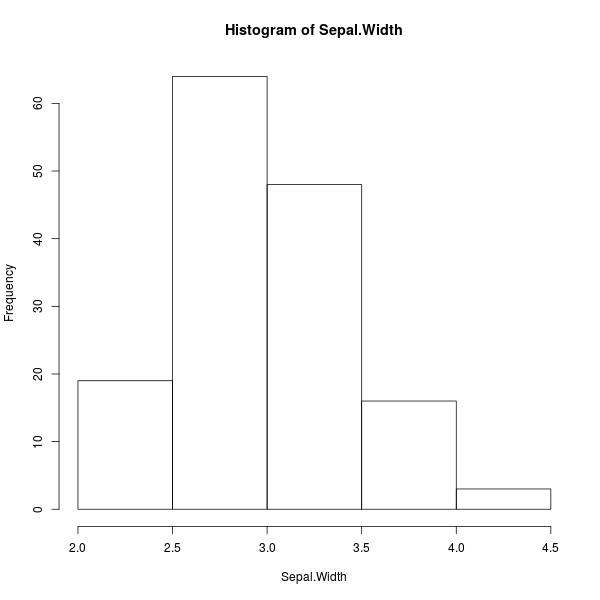
ภาพที่ 9: ฮิสโตแกรมความกว้างกลีบเลี้ยงดอกไอริส โดยขีดเส้นแบ่งช่วง 4 ครั้ง
หรือเราอาจระบุตำแหน่งทั้งหมดของรอยต่อระหว่างช่วงที่ต้องการแบ่งก็ได้ โดยเรามีอิสระที่ไม่จำเป็นต้องเลือกให้แต่ละช่วงมีขนาดเท่ากัน
> hist(Sepal.Width, breaks=c(2,2.1,2.4,2.7,3.0,3.3,3.6,3.9,4.4))
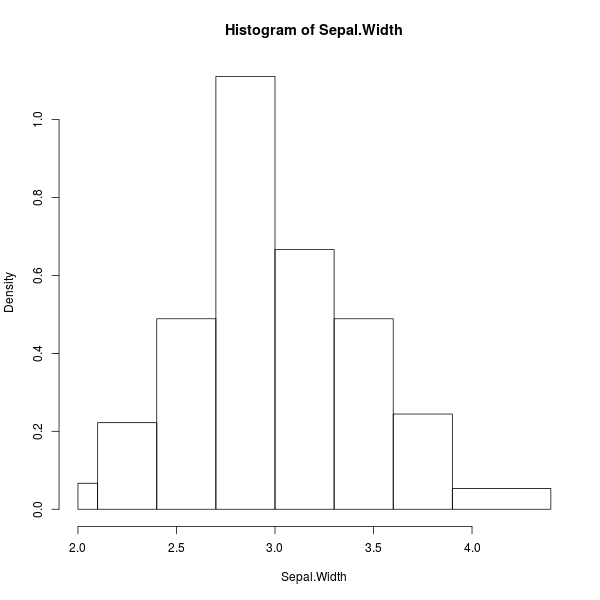
ภาพที่ 10: ฮิสโตแกรมความกว้างกลีบเลี้ยงดอกไอริส โดยแบ่งขนาดช่วงไม่เท่ากัน
หากแต่ละแท่งในฮิสโตแกรมมีความกว้างไม่เท่ากัน (เช่น ในภาพที่ 10) แกนแนวตั้งในพล็อตจะไม่ได้แสดงจำนวนการเกิดของข้อมูลอีกต่อไปแล้ว แต่มันคือค่าความหนาแน่นของข้อมูลในแต่ละช่วงแทน โดยใช้กฎว่าพื้นที่ของสี่เหลี่ยมทุกแท่ง (ขนาดช่วงคูณความหนาแน่น) รวมกันจะต้องได้เท่ากับหนึ่งหน่วยเสมอ ดังนั้นหากเราขยายขนาดของช่วงโดยที่มันยังครอบคลุมข้อมูลได้เป็นจำนวนเท่าเดิม แท่งข้อมูลแทนช่วงนั้นก็จะมีความสูงลดลงไปนั่นเอง (เช่น ขยายขนาดของช่วงสุดท้ายจาก 3.9-4.4 ไปเป็น 3.9-5.0)
พล็อตกล่อง (box plot)
พล็อตกล่องนั้นไม่ได้แสดงจำนวนการเกิดของข้อมูลเป็นช่วงๆ เหมือนอย่างฮิสโตแกรมแล้ว แต่จะแสดงข้อมูลด้วยค่าสรุปจากควอร์ไทล์แทน ลองพิจารณาตัวอย่างต่อไปนี้
> boxplot(Sepal.Length)
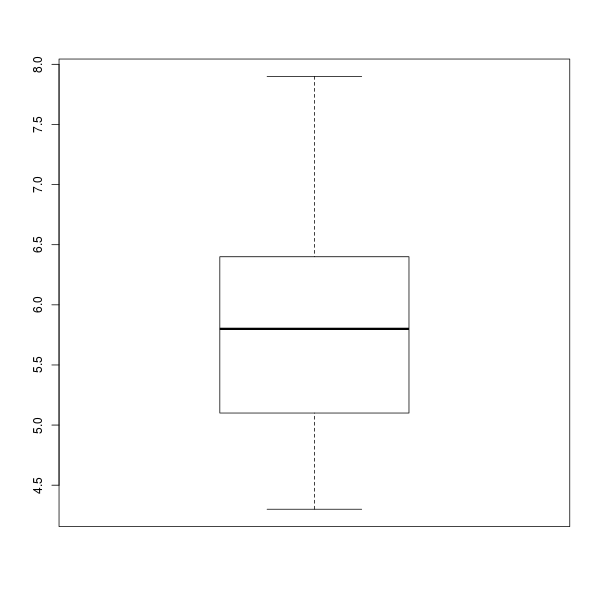
ภาพที่ 11: พล็อตกล่องความกว้างกลีบเลี้ยงดอกไอริส
ผลลัพธ์ที่ได้จากพล็อตกล่องในภาพที่ 11 มีลักษณะเป็นกล่องสี่เหลี่ยมที่ลอยอยู่และมีขายื่นออกมาข้างบนและล่าง เส้นหนาที่ลากผ่านกลางกล่องคือมัธยฐาน ขอบล่างของกล่องคือควอร์ไทล์ที่ 1 และขอบบนของกล่องคือควอร์ไทล์ที่ 3 สำหรับขาแต่ละข้างที่ยื่นออกมาจากตัวกล่องนั้น สุดปลายขาล่างคือค่าต่ำสุด และสุดปลายขาบนคือค่าสูงสุดนั่นเอง
แม้ว่าพล็อตกล่องจะแสดงการกระจายได้ไม่ละเอียดเท่าฮิสโตแกรม แต่ข้อได้เปรียบของพล็อตกล่องก็คือมันสามารถแสดงข้อมูลหลายๆ ชุดเปรียบเทียบกันได้ง่ายกว่า ดังจะเห็นได้ในภาพถัดไป
> boxplot(iris[1:4])
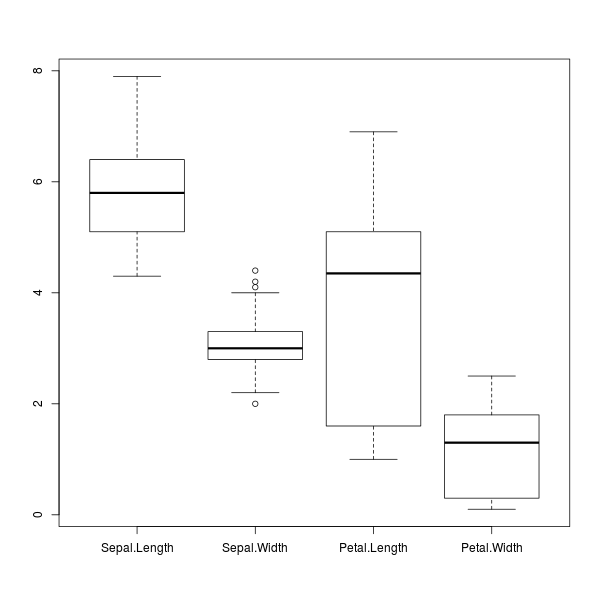
ภาพที่ 12: พล็อตกล่องข้อมูลตัวเลขทั้งหมดของดอกไอริส
การเปรียบเทียบการกระจายในภาพที่ 12 แสดงให้เห็นชัดว่า ความกว้างกลีบเลี้ยง ( Sepal.Width
) มีการกระจายตัวต่ำที่สุด และในทางกลับกัน ความยาวกลีบดอก ( Petal.Length
) ก็มีการกระจายตัวมากที่สุด นอกจากนี้มันยังบอกตำแหน่งข้อมูลได้อีกด้วยว่า ความยาวกลีบเลี้ยง ( Sepal.Length
) มีค่ามากกว่าความกว้างกลีบดอก ( Petal.Width
) เสมอ
จุดเด่นอีกอย่างของพล็อตกล่อง คือมันสามารถแยกให้เห็น ค่าผิดปรกติ (outlier) ได้ง่าย โดยแสดงเป็นจุดที่อยู่ไกลเลยขากล่องไปนั่นเอง หลักเกณฑ์สำหรับคัดแยกค่าผิดปรกติ คือ ค่านั้นมีค่าน้อยกว่า/มากกว่าค่าจากควอร์ไทล์ที่ 1/ควอร์ไทล์ที่ 3 อยู่ 1.5 เท่าของพิสัยระหว่างควอร์ไทล์ตามลำดับ ซึ่งอาจตีความหมายได้ว่า ค่านั้นเกิดจากการจดบันทึกข้อมูลผิดเพี้ยน และควรลบมันทิ้งก่อนนำข้อมูลไปประมวลผลต่อไป
เขียนโปรแกรมด้วย R
จากหัวข้อก่อนๆ เราอาจสัมผัสได้ถึงพลังของ R ในการใช้งานคำนวณโต้ตอบแบบกระดาษทด (REPL) ไปแล้ว แต่ในการใช้งานที่ซับซ้อนขึ้นไปนั้น การพิมพ์คำสั่งใหม่ทุกครั้งที่ต้องการคำนวณอาจไม่สะดวกเท่าไรนัก การจัดเรียบเรียงคำสั่งต่างๆ เหล่านั้นลงในไฟล์ แล้วเรียกใช้งานเป็นโปรแกรมแยกที่ทำงานทุกอย่างด้วยตัวเอง หรือนำเข้าฟังก์ชันสำคัญจากไฟล์นั้นมาใช้งานต่อ จึงเป็นทางเลือกที่มีประสิทธิภาพกว่าการพิมพ์คำสั่งใหม่ทุกครั้งเสมอ
เราจะแสดงการเขียนโปรแกรมในภาษา R โดยยกตัวอย่างผ่าน ปัญหานักสะสมคูปอง ที่ถามคำถามง่ายๆ แต่น่าสนใจว่า นักสะสมคูปองต้องเปิดซองเสี่ยงโชคกี่ครั้งถึงจะเก็บคูปองที่สุ่มแจกได้ครบทุกแบบ
หมายเหตุว่าสำหรับหัวข้อนี้ โค้ดที่แสดงจะไม่มีสัญลักษณ์ >
นำหน้า ซึ่งก็คือทุกคำสั่งต่อไปนี้ไม่ได้สั่งงานผ่าน REPL และรอดูคำตอบแล้ว แต่เป็นการเขียนคำสั่งต่างๆ เหล่านี้ลงไปในไฟล์สคริปต์แทน ใครที่ต้องการทดลองตามขอให้สร้างไฟล์ใหม่ชื่อ coupon.R
แล้วคัดลอกโค้ดต่างๆ ที่กำลังจะปรากฏในหัวข้อนี้ลงไปยังไฟล์ดังกล่าว
ประกาศฟังก์ชัน
ฟังก์ชันในภาษา R นั้น เมื่อมองอย่างผิวเผินแล้วอาจดูไม่แตกต่างจากฟังก์ชันในภาษาอื่น การประกาศฟังก์ชันทำได้โดยใช้คำสำคัญว่า function
ตามด้วยพารามิเตอร์ แล้วจบด้วยเนื้อหาในฟังก์ชันนั้นๆ สิ่งสำคัญที่ต่างออกไปจากภาษาอื่น คือการตั้งชื่อให้ฟังก์ชันจะต้องทำด้วยวิธีเดียวกันกับการประกาศตัวแปรเท่านั้น
random.int <- function(n) { sample.int(n, 1) }
โค้ดข้างต้นสร้างฟังก์ชัน random.int
สำหรับสุ่มเลขจำนวนเต็มระหว่าง 1
ถึง n
ขึ้นมาหนึ่งตัว
ข้อสังเกตสำหรับการเขียนเนื้อหาฟังก์ชัน นั่นก็คือตอนจบฟังก์ชันไม่จำเป็นต้องสั่ง return
เพื่อบอกว่าต้องการคืนค่าใดจากฟังก์ชัน แต่คำสั่งสุดท้ายในฟังก์ชันจะถูกส่งคืนค่าโดยอัตโนมัติ
วนซ้ำจนกว่าจะผิดเงื่อนไข (while loop)
การวนซ้ำจนกว่าจะผิดเงื่อนไข ประกาศโดยคำสำคัญ while
และมีโครงสร้างเฉกเช่นภาษาทั่วไป
random.coupon <- function(...) {
count <- 0
have.coupon <- logical(...)
while (!all(have.coupon)) {
have.coupon[random.int(...)] <- TRUE
count <- count + 1
}
count
}
โค้ดข้างต้นสร้างฟังก์ชัน random.coupon
สำหรับนับว่าต้องเปิดซองชิงโชคกี่ครั้ง ถึงจะได้คูปองครบ n
แบบ โดยใช้เทคนิคการวนซ้ำแบบ while
ในบรรทัดที่ 4 ถึง 7
ข้อสังเกตที่มาคู่กับการวนซ้ำเช่นนี้ คงหนีไม่พ้นการเพิ่มค่าตัวนับในแต่ละรอบที่วน ในภาษาทั่วไปอาจใช้เครื่องหมาย ++
หรือ +=
เพื่อเพิ่มค่านั้นก็ได้ แต่สำหรับภาษา R ที่ไม่มีตัวดำเนินการทั้งสองให้ใช้แล้ว จึงจำเป็นต้องเขียนเต็มยศ ดังเช่นที่เห็นได้จากบรรทัดที่ 6 ในโค้ดข้างต้น
ข้อสังเกตอื่นๆ อยู่ตรงการประกาศฟังก์ชันที่ระบุพารามิเตอร์ว่า ...
ซึ่งมีความหมายว่าฟังก์ชันนี้สามารถรับอาร์กิวเมนต์ได้ไม่จำกัด และจะส่งต่อค่าในอาร์กิวเมนต์ที่รับเข้ามาไปยังฟังก์ชันอื่นๆ ในเนื้อหาฟังก์ชันนี้ที่เรียกใช้ ...
เป็นอาร์กิวเมนต์ (ตัวอย่างเช่น ถ้าเรียกใช้ฟังก์ชัน random.coupon(42)
ค่า 42
นี้จะถูกส่งไปเป็นเรียกใช้งานฟังก์ชัน logical(42)
ต่อไป)
วนซ้ำสำหรับของแต่ละชิ้น (for loop)
การวนซ้ำสำหรับของแต่ละชิ้น ประกาศโดยใช้คำสำคัญ for
ตามด้วยตัวแปรสำหรับรับสิ่งของในแต่ละรอบ แล้วตามด้วยเวกเตอร์ของสิ่งของทั้งหมดที่ต้องการวนซ้ำ (เช่นเดียวกับ foreach
ในหลายภาษา)
sample.coupon <- function(n, size=10*n) {
result <- NULL
for (i in 1:size) {
result <- c(result, random.coupon(n))
}
result
}
โค้ดข้างต้นสร้างฟังก์ชัน sample.coupon
สำหรับทดลองหลายๆ ครั้งว่าแต่ละครั้งต้องสุ่มเปิดซองชิงโชคกี่ครั้ง โดยใช้เทคนิคการวนซ้ำแบบ for
ในบรรทัดที่ 3 ถึง 5
จุดที่น่าสนใจอยู่ที่การประกาศพารามิเตอร์โดยกำหนด อาร์กิวเมนต์ปริยาย (default argument) ที่สามารถอ้างอิงไปยังอาร์กิวเมนต์อื่นของฟังก์ชันนี้ได้ทันที
ทำหรือไม่ตามแต่เงื่อนไขจะกำหนด (if-else)
การตรวจสอบถ้า-แล้ว สามารถใช้คำสำคัญได้เช่นเดียวกันกับภาษาทั่วไป คือ if
else if
และ else
if (!interactive()) {
args <- commandArgs(TRUE)
if (length(args) == 1) {
filename <- "sample-coupon.png"
} else if (length(args) == 2) {
filename <- args[2]
} else {
stop("wrong number of argument!")
}
png(filename, width=800, height=800)
arg.list <- list(x=as.numeric(args[1]))
do.call(hist, list(substitute(sample.coupon(x), arg.list)))
dev.off()
}
โค้ดข้างต้นจะตรวจสอบว่าโปรแกรมนี้ถูกเรียกใช้งานผ่าน REPL หรือไม่ ถ้าไม่ใช่แล้วจึงตรวจสอบต่อว่าการเรียกใช้งานมีอาร์กิวเมนต์ใดบ้าง หากอาร์กิวเมนต์ถูกต้องจะสร้างไฟล์ภาพฮิสโตแกรมของการทดลองหาคำตอบของคำถามนักสะสมคูปองขึ้นมา
เรียกใช้โปรแกรม
ถึงตอนนี้หากใครพิมพ์ตามโค้ดข้างต้นทั้งหมด ก็จะได้ไฟล์สคริปต์ภาษา R มาหนึ่งโปรแกรมแล้ว (ส่วนใครไม่ได้พิมพ์ตาม แต่ยังอยากทดลองต่อ สามารถ ดาวน์โหลดโค้ดข้างต้นได้ที่นี่ ) เราสามารถเรียกใช้โปรแกรมดังกล่าวผ่าน terminal/cmd ได้ดังนี้
$ Rscript coupon.R 30
หรือจะนำเข้าฟังก์ชันจากไฟล์ดังกล่าวเข้ามายัง REPL เพื่อประยุกต์ใช้แบบโต้ตอบก็ย่อมได้
> source("PATH/TO/SCRIPT/coupon.R")
> hist(sample.coupon(30))
ไม่ว่าจะเรียกด้วยวิธีไหน ผลลัพธ์ที่ได้จะมีหน้าตาหนีไม่พ้นภาพที่ 13 ไปเท่าใดนัก (แม้ว่าอัลกอริทึมดังกล่าวจะอาศัยการสุ่มก็ตาม)
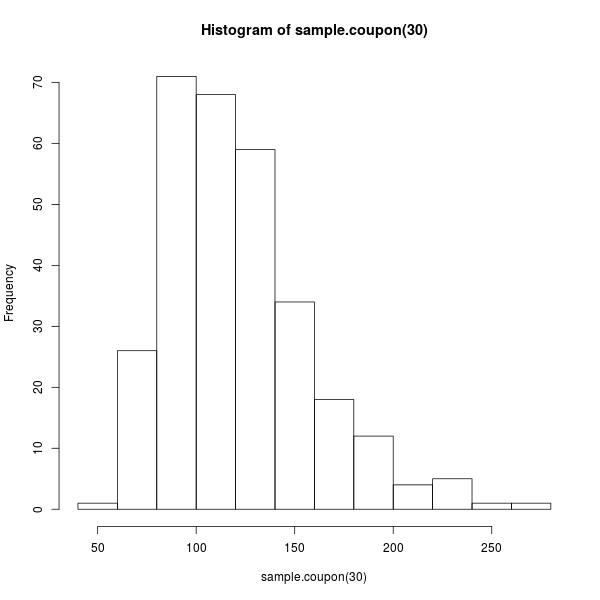
ภาพที่ 13: ฮิสโตแกรมคำตอบจากการทดลองปัญหานักสะสมคูปอง เมื่อมีคูปองแตกต่างกัน 30 แบบ
ดาวน์โหลดแพ็กเกจเสริมความสามารถ
จากหัวข้อที่ผ่านๆ มา หลายคนอาจมองเห็นแนวทางอันหลากหลายที่จะประยุกต์ใช้ภาษา R เพื่อช่วยแก้ปัญหาที่ต้องข้องเกี่ยวกับข้อมูลกันไปแล้ว แต่ความสามารถเท่านั้นจากตัวภาษา R เพียงอย่างเดียว ก็ยังนับว่าน้อยนิดเมื่อเทียบกับแพ็กเกจเพิ่มความสามารถที่ชุมชนอุทิศให้
โดยสถานที่จัดเก็บแพ็กเกจหลักอย่างเป็นทางการของภาษาดังกล่าวมีชื่อว่า CRAN (Comprehensive R Archive Network) ซึ่งปัจจุบันได้โฮสต์แพ็กเกจเสริมความสามารถกว่าหนึ่งหมื่นแพ็กเกจให้เลือกใช้งาน
วิธีการดาวน์โหลดแพ็กเกจเหล่านี้ก็ไม่ยาก เพียงแค่มีชื่อแพ็กเกจเหล่านั้นไว้ในใจ แล้วเปิด REPL ขึ้นมาเรียกฟังก์ชันต่อไปนี้
> install.pacakges("packageName")
โดยเปลี่ยน "packageName"
เป็นชื่อแพ็กเกจที่ต้องการ หลังจากนั้นจะมีตัวเลือก mirror ของประเทศต่างๆ ขึ้นมา เลือกประเทศที่อยู่ใกล้ที่สุดเพื่อความเร็วในการดาวน์โหลด แล้วรอโปรแกรมดาวน์โหลดและติดตั้งแพ็กเกจเหล่านั้น
หลังจากติดตั้งเสร็จสิ้น เมื่อต้องการนำเข้าแพ็คเกจเหล่านั้นมาใช้งาน ก็ทำได้โดย
> library(packageName)
ต่อไปนี้จะขอแนะนำแพ็กเกจที่น่าสนใจจำนวนหนึ่ง (หากสั่ง library()
แล้วพบข้อความแสดงความผิดพลาด อย่าลืมว่าต้องดาวน์โหลดแพ็กเกจเหล่านั้นก่อน)
กราฟเครือข่าย
กราฟเครือข่ายสามารถบ่งบอกความสัมพันธ์ในข้อมูลผ่านจุด (node) และเส้นเชื่อม (edge) ตัวอย่างข้อมูลที่เราคุ้นเคยกันดีคงหนีไม่พ้นความสัมพันธ์บนเครือข่ายสังคมออนไลน์ แต่ข้อมูลชนิดอื่นๆ ก็อาจถูกแปลงให้เป็นกราฟเครือข่ายได้ เช่น แผนที่ทางหลวง
> library(igraph)
> plot(make_graph("petersen"))
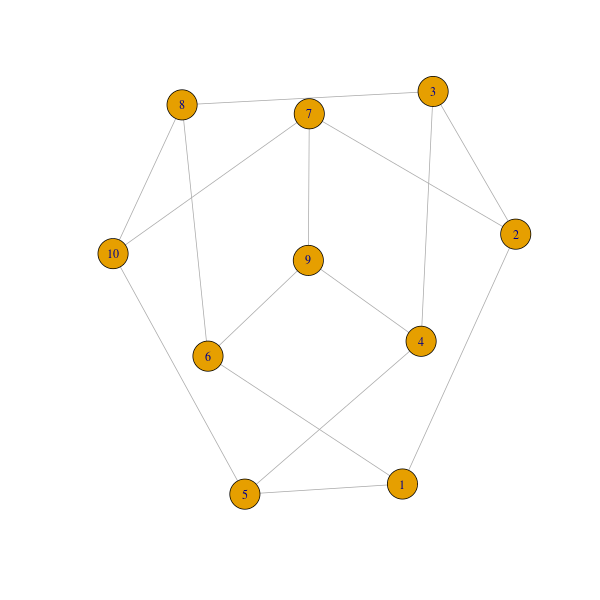
ภาพที่ 14: กราฟเครือข่ายที่มีการเชื่อมโยงแบบ กราฟปีเตอร์เซน
ทำนายอนาคต
สำหรับข้อมูลที่มีแกนหนึ่งเป็นแกนเวลา เช่น ข้อมูลดินฟ้าอากาศ จำนวนประชากร หรือกระทั่งราคาหุ้น หากข้อมูลเหล่านั้นมีรูปแบบที่เกิดซ้ำมากพอ เราก็อาจทำนายอนาคตของข้อมูลนั้นได้
> library(forecast)
> plot(forecast(nottem))
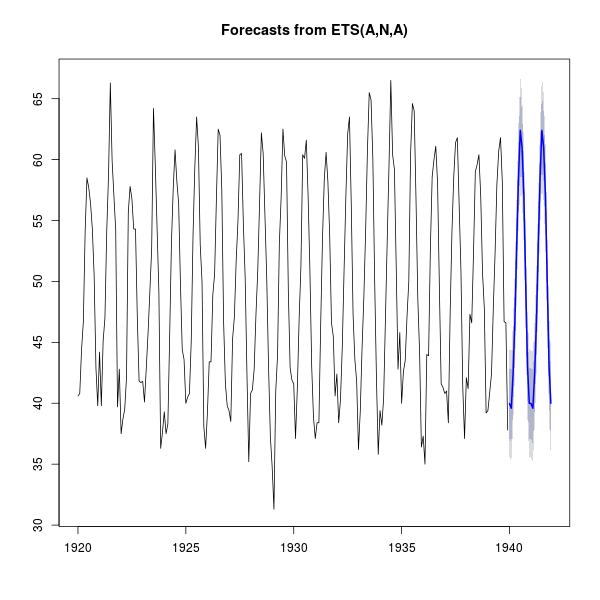
ภาพที่ 15: พยากรณ์อุณหภูมิของเมืองนอตทิงแฮม (เส้นสีน้ำเงิน)
แผนที่โลก
นอกจากการพล็อตข้อมูลเชิงสถิติแล้ว R ยังสามารถพล็อตแผนที่โลกได้อีกด้วย
> library(maps)
> library(mapdata)
> map("world2Hires", xlim=c(110,190), ylim=c(-50,0))
> points(quakes[2:1], pch=".", col="red")
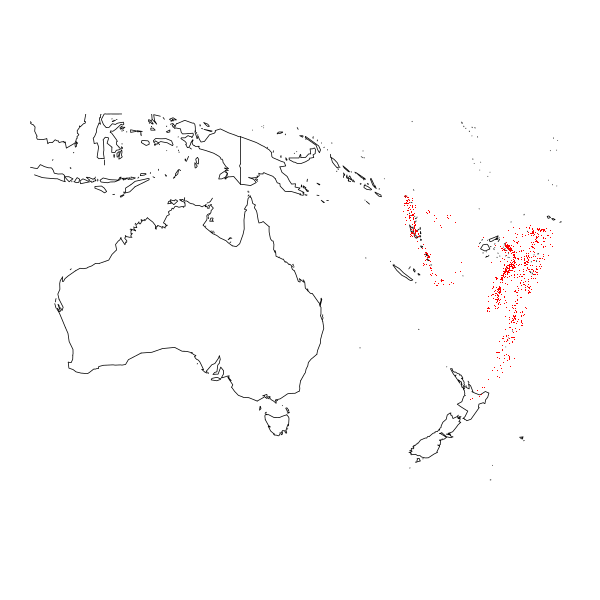
ภาพที่ 16: แผนที่โลกพร้อมตำแหน่งเกิดแผ่นดินไหว (จุดสีแดง) ใกล้ฟีจี
สรุป
บทความตอนนี้แสดงให้เห็นความสามารถสำคัญๆ ในภาษา R โดยไล่ตั้งแต่เรื่องพื้นฐานอย่างชนิดตัวแปร ไปจนถึงการดาวน์โหลดแพ็กเกจเพิ่มความสามารถและเขียนโปรแกรมมาแก้ไขปัญหาจริง ใครที่อดทนอ่านและทำความเข้าใจได้จนถึงบรรทัดนี้ ก็คงพูดไม่ผิดว่าคุณรู้จักและสามารถเขียนโค้ดในภาษา R ได้แล้ว
อย่างไรก็ตาม บทความนี้ก็ไม่ได้กล่าวถึงทุกเรื่องที่ควรรู้ในภาษา R และตัวอย่างการคำนวณทางสถิติก็ยังอยู่ในระดับขั้นพื้นฐานเป็นอย่างมาก ใครที่ต้องการนำภาษา R ไปประยุกต์ใช้งานอย่างจริงจัง หรือวาดฝันไว้ว่าต้องการเป็นนักวิทยาศาสตร์ข้อมูล (data scientist) ก็คงต้องบอกว่าจงตั้งใจศึกษาตัวภาษาและวิชาสถิติเพิ่มเติม
เพราะการเรียนรู้ไม่มีวันสิ้นสุด และการเรียนรู้จะบรรลุผลสูงสุดเมื่อสามารถประยุกต์ใช้ความรู้นั้นเพื่อสร้างสรรค์ประโยชน์ได้
ภาคผนวก
ติดตั้งโปรแกรมบนเครื่อง
การติดตั้ง R นั้นสามารถทำได้อย่างง่ายดาย เพียงแค่เข้าไปยัง เว็บไซต์หลักของภาษา R แล้วตามลิงก์ที่เขียนคำว่า "download R" จะพบกับรายชื่อ mirror ต่างๆ ทั่วโลกที่ทำสำเนาโครงการภาษา R ไว้ เลือกตัวเลือกที่อยู่ใกล้เคียงตำแหน่งปัจจุบันมากที่สุดเพื่อความเร็วในการดาวน์โหลด (สำหรับประเทศไทย มี mirror ของมหาวิทยาลัยสงขลานครินทร์ สำหรับสำเนาดังกล่าว) เมื่อเข้าไปแล้ว จะพบกับตัวเลือกให้ดาวน์โหลดโปรแกรมได้ทั้งบน Windows, OS X และ Linux โดยมีรายละเอียดต่างกันเล็กน้อย ดังนี้
- Windowsเลือกดาวน์โหลดไฟล์ติดตั้ง .exe จากแฟ้ม "base" มาติดตั้งก็เพียงพอแล้วสำหรับบทความนี้
- OS Xดาวน์โหลดไฟล์ติดตั้ง .pkg รุ่นใหม่ล่าสุดจากหน้าดาวน์โหลดของ OS X มาติดตั้งได้เลย
- Linuxเนื่องจากความหลากหลายทางดิสโทร การหาไฟล์ติดตั้งที่ถูกต้องจากหน้านี้อาจเป็นเรื่องยุ่งยากเกินจำเป็น เราอาจเลือกสั่งเพียงคำสั่งต่อไปนี้ผ่าน terminal แทน
-
apt install r-baseสำหรับดิสโทร Debian/Ubuntu -
yum install Rสำหรับดิสโทร Red Hat/Fedora
-
หลังจากติดตั้งโปรแกรมสำเร็จแล้ว ผู้ใช้ OS X/Linux ไม่ต้องทำอะไรต่อ ส่วนผู้ใช้ Windows ควรแก้ไขตัวแปร PATH
โดยเพิ่มตำแหน่งที่ติดตั้งโปรแกรม R (เช่น C:\Program Files\R\R-3.4.1\bin\x64
) ต่อท้ายตัวแปรนั้น เพื่อให้สามารถเรียกโปรแกรม R ผ่าน cmd ได้ในภายหลัง











Comments
ความแตกแตก ?
กระพริบ => กะพริบ
เรียบร้อยครับ
รายระเอียด => รายละเอียด
เท่าไหร่ => เท่าไร
สากกระเบือ => สากกะเบือ
เรียบร้อยครับ
login เข้ามาเพื่อของคุณโดยเฉพาะเลย ขอบคุณมากนะครับที่เขียนบทความสรุปเรื่องภาษา R มาเสียยาวเลยครับ เดี๋ยวมาอ่านต่อครับผม ตอนนี้เอาไปแชร์ก่อน :D
ขอบคุณครับเคยใช้ตอนเรียนวิชา TextMining ใช้งานสะดวกดีครับ ติดแต่ R ภาษามันออกประหลาดๆ ไปหน่อย แต่โดยรวมก็ถือว่าใช้สะดวกดีครับ Lib โหลดง่ายมาก
บล็อกส่วนตัวที่อัพเดตตามอารมณ์และความขยัน :P
Ubuntu add repo เองโลดครับ ไม่งั้นจะได้ version ไม่ล่าสุดมา
ใครอยากเรียนแบบกึ่งละเอียดก็ตามลิงค์นี้ครับ(สนุกมาก) http://tryr.codeschool.com/
น่าลองครับ ขอบคุณครับ
นั่งลองที่ datacamp อยู่พอดีเลย
นึกว่าอ่านงานวิจัย เดี๋ยวมาต่อครับ เขียนได้สุดยอด
ขอบคุณที่แบ่งปันความรู้ครับผม
ดีกว่า Python อย่างไรบ้าง
ทำ stat ละเมียดกว่าครับ
R = เกิดมาเพื่อสถิติPython = เกิดมาเพื่อโปรแกรมมิ่ง
ปีที่แล้ว Google รับพนักงานมี requirement เรื่อง R โดยเฉพาะเลยล็อตนึง
วิทยากรของกูเกิ้ลเองก็ยังบอกว่าเขาใช้ R ในขั้นสุดท้ายของ Analytic อยู่ประมาณว่า Automate tool ยังไงยังต้องจบขั้นสุดท้ายใน R
หรือจะดีจะร้ายยังไง สุดท้ายความจริงที่ว่าเวลาเจอข้อมูลก้อนใหญ่ๆ มันไม่มีปัญหาเหมือน Spss แค่นี้ก็น่าสนใจแล้ว
Shut up and ヽ༼ຈل͜ຈ༽ノ raise your dongers ヽ༼ຈل͜ຈ༽ノ
เห็นstyle แล้วนึกถึง mathlab
ขอบคุณมากๆเลยครับ เป็นประโยชน์กับผู้ที่ไม่รู้จักภาษานี้มากๆเลย เยี่ยมมาก
..: เรื่อยไป
ขอบคุณครับ เพิ่งรู้จักภาษา R ก็วันนี้แหล
อ่านช่วงแรกๆ นึกว่า กำลังเขียน matlab
เป็นประโยชน์มากครับ ขอบคุณ
ใช้ได้หลากหลายดีครับที่สำคัญมันฟรี
ขอบคุณมากครับ อ่านอยู่นานเลยครับ :)
ขอบคุณบทความมาก เขียนดีครับใช้เวลาอ่านอยู่นานเหมือนกัน นึกไม่ออกเลยว่าใช้เวลาและพลังในการเขียนขนาดไหน
เดือนนิดๆ ครับ
ขอบคุณมากครับ