全58件 (58件中 1-50件目)
-
お詫び
苦学楽学塾サイトを開始して1年が経過しました。2021年度の主要大学入試問題の検討もほぼ終わりを迎えつつあります。6月末頃までは、2021年度の問題を検討していきます。7月からは、本年度の見直しを行い、合わせて、基礎事項へのリンクを貼る作業を行うつもりです。現状では、苦学楽学塾サイトでは問題なく行えている数式表示が、苦学楽学塾ブログではできず、まだ、原因調査中段階です。色々とメールなど頂いておりますが、質問などへのお答え(苦学楽学塾ブログで行う予定でいます)ができない状態で、お問い合わせにお答えができず申し訳ありません。そもそも、問い合わせなどを受け付けるメール・アドレスの設定がうまくできずに苦しんでいる、という有様です。鋭意努力中ですので、宜しくお願い致します。追伸.メール設定成功しました。いつもながら、わかってみればくだらないことが原因でした。申し訳ありません。
2021.05.16
コメント(0)
-
再開します
CFV21の頃の最後のコメントより10年近く経過してしまいました。 その間も、何とか、継続できないかともがいておりましたが、残念ながら、格安料金としたのにもかかわらず、会員数が増えることなく、生活苦の中で、他のアルバイトで食うカネを稼ぐのに精一杯の状況に至り、CFV21の最後の頃は、会員サポートさえ行えず、ご迷惑をおかけしてしまった方には、まことに申し訳なく思っております。このコメントとは別にコメントさせて頂きますが、会費の返還をさせて頂きたく、当時の会員の方、ご連絡頂ければ幸いです。 生活の不安が解消した今、再度、「零からの挑戦」をさせて頂きたく出て参りました。 CFV21の21は21世紀の21でしたが、一国二制度であったはずの香港への中国政府の強硬姿勢、政治的リーダーによる米国国内の分断、EUの分裂、そして新型ウィルスの蔓延、など、世界を巡る状況は厳しく、21世紀が「明るい希望の世紀」と言うのはあまりに楽観主義的に思えます。 「ゼロからの挑戦」というCFV21プロジェクトで目指したものを変えるわけではありませんが、再開にあたり、心機一転、塾名を「苦学楽学塾」と改めさせて頂きました。それとともに、会費も改定させて頂きます。CFV21の会費では300人くらいの会員が集まらないと運営続行は不可能です。「苦学楽学塾」では従前の活動継続とともに、色々な活動をさせて頂きたいと思っております。 同業者の皆様、大学入試に関わる皆様、教鞭を振るっていらっしゃる先生方、明日の日本を支えるべく日夜勉学に励んでいらっしゃる受験生の皆様、ぜひ、宜しくお願いいたします。
2020.06.16
コメント(0)
-
2011年センター試験物理
センター試験物理をやってみました。来年以降、受験をお考えの方のために、感想を書いておきます。既に、大学入試センターより、中間集計結果が出ていますが、平均点は64.08点でやや高めです。例年と特に変化はなく、全体的に、易しい、という雰囲気はしませんが、ボリュームが少ない感じで、迷うような問題でも、じっくり考えて取り組めたのではないかと思います。もう少し易しくてもよいような気がしますが、物理現象を物理として捉えるような問題が工夫されていて、基礎学力を見るセンター試験の趣旨として適切な問題のように感じました。(物理は、CFV21サイトに問題・解答をアップしませんので、ご了承ください)第1問、全分野からの小問集合というのは昨年までと同じです。問1は、固定端の反射で位相がπずれることを図示するとどうなるか、という問題なのですが、私が持っている教科書では、「参考」として書かれている内容なので、困った受験生がいたかも知れません。位相がπずれると、波形は反転します。入射波と反射波で進む方向が逆になることにも注意が必要です。問2は、回転する棒の速さをエネルギーから考える問題で、カンで答えると失敗します。式を立てて、回転角が45度と90度の場合で考えれば正解はわかります。「棒」ということに惑わされた受験生がいたかも知れません。問3は、静電誘導の基本問題。問4は、音波が屈折するときどう進むか、という問題ですが、光波と同じです。問5は、モーメントとばねの弾性力の問題。これは、式を立てて計算しますが簡単です。問6は、次元の問題で、珍しいテーマなので、びくついた受験生もいたかも知れませんが、常識の範囲内です。第2問は、電磁気分野で、Aは非直線抵抗、Bは電磁誘導がテーマです。Aは、理系で慣れている受験生には、グラフの中の特徴的な点を読むだけなので何でもありませんが、非直線抵抗を敬遠して勉強した人は手がつかなかったでしょう。Bは、右ねじの法則やレンツの法則などから考えればよいのですが、これも差がつく問題です。第3問は、波動分野の問題です。Aはレンズの問題ですが、物体から出て光軸に平行に進む光線、レンズの中心を通る光線、焦点を通る光線を作図して考える、という、基本問題です。Bは2音源から出る音波の干渉の問題です。波の公式でちょっとした計算をしますが、あとは、教科書に書いてある内容です。問題文がやや不親切なところがあるので注意が必要です。第4問は、力学分野の問題です。Aは連結バネの問題かと思うとそうではなく、エネルギー保存の式を立てる問題です。選択肢がややまごつくかも知れません。でも、時間的に余裕があるので、選択肢に出てくる文字を使って式を書き直せば解決します。Bは、センターとしては良い問題です。ひもでつながれた2物体が粗い床の上を滑るときの物理的状況を推理する内容になっていて、楽しく興味深く考えることができるでしょう。Cは、気体の問題で、浮力が出てくるのかと思うとそうでもなく、問5は、定圧変化に気づいてシャルルの法則を考え、問6は、容器上面に働く力のつり合い、液面高さでの力のつり合いの式を立てれば解答できます。問6は少々難しく感じるかも知れませんが、しばしば、国公立大・難関私大で見かける問題なので、経験者なら正解できるでしょう。大学入試問題研究サイト
2011.01.23
コメント(0)
-
2011年センター試験数学IIB
センター試験数学IIBをやってみました。来年以降、受験をお考えの方のために、感想を書いておきます。昨年から数学IIBは幾分易しくなっていますが、ことしも引き継がれています。微積や空間ベクトルの計算が複雑化しないように、また、途中でミスに気がつけるように、という配慮が見られるようになりました。以下、各設問を見ていきます。第1問[1]は、三角関数を含む関数の最大最小の問題です。置き換えを行って2次関数の最大最小に持ち込むのですが、誘導がついているので、指示通りに計算するだけです。半角の公式と合成の公式を使うだけなので、ここは落とせません。[2]は与えられた対数不等式を満たす自然数を求める問題です。最初は底の変換を行って不等式を解くだけです。ここも落とせません。最後の枠が、どうするのか悩むかも知れませんが、自然数xに10とか11とか12とか、値をあてはめてみれば、答えはすぐにわかります。第2問は微積分の素直な計算問題です。放物線がy=x2という簡単なもので、微積分の計算も複雑にならないように設定されていて、基礎事項の理解を見ることができるように、従来の計算問題よりもずっと工夫されています。また、問題文の中に、計算結果が正しいかどうか見直すことを促すような記述が見られるのも改善点の一つです。センター試験の微積分の問題としては、本問のようなもので良いのではないか、と、私は思います。第3問は数列の問題です。漸化式の問題としても解くことが可能な問題ですが、階差数列を考えて解くような誘導がついているので、これで考えるしかありません。誘導に乗れば、指示通りに手を動かすだけです。後半は、(等差数列)×(等比数列)の形の数列の和を求める問題で、これもよくある問題です。ここは、少し大変な計算になります。ですが、実力派の受験生なら、何でもないでしょう。ただ、個人的には、もう少し基本的な問題でも良いのではないか、という気がします。第4問は空間ベクトルの問題です。空間ベクトルの問題なので、どうしても、計算は面倒になります。内積の値を最初から与えておく、というような工夫をすれば、もう少し計算力よりも思考力を見る問題も可能だと思います。親切な誘導がついているので、誘導通りにミスなく進めて行けば、最終解答に問題なくたどりつけるでしょう。従来の空間ベクトルの問題と比較すれば取り組みやすい問題です。受験生の皆さんは、この程度の問題で最後までミスなく計算を進めていけるように、トレーニングをみっちり行って頂きたいと思います。全般的に、実力が結果に反映されるように、工夫された出題がなされるようになってきました。一時は、東北大学で、センター試験結果は2次試験の結果と全く相関がない、などとする調査結果も公表されたりしましたが、本年のような問題であれば、相関はかなり高くなるだろうと期待できます。今後も、こうした数学の実力が反映されるような問題が出題されるように期待したいと思います。追記(1月23日)あれあれ、大学入試センターの中間集計では、平均点は52.46点で予想外に低くなっています。ことしの問題で、数学IAが高く、数学IIBが低いというのは不思議ですね。数学IAで疲れてしまった、というようなことでもあるのでしょうか?数学IA、IIBともに標準的な出題で、数学をよく勉強していた受験生には取り組みやすかった、というのは共通です。大学入試問題研究サイト
2011.01.16
コメント(0)
-
2011年センター試験数学IA
センター試験数学IAをやってみました。来年以降、受験をお考えの方のために、感想を書いておきます。ことしも昨年同様、手間のかかる問題で、平均点は高くならないだろうと思います。どこかで、計算ミスなどによってハマったりすると時間が足りなくなってしまうでしょう。基礎事項をしっかりマスターしておくとともに、過去問で計算練習を積んでおく必要があります。第1問[1]は、分母の有理化の計算問題です。ありふれた問題ですが、不等式の解を求めるところで、先に行っている計算結果を使うことに気づかないとムダに時間を使うことになります。ここは落とせません。[2]は論理の問題ですが、これは例年になく難しかったと思います。(1)で、適当に値をあてはめて条件pと条件qの関係を推測するように、ということなんでしょうが、こんな設問を出すくらいなら、論理の問題を出題すべきではないと、私は思います。もちろん、例年の問題も一々証明をして、などという必要はありませんが、今年は、ほとんどの受験生がカンで答えて、それでも、「十分条件」、「必要条件」、「対偶」の意味をしっかり勉強していた人が正解できたでしょう。第2問は2次関数のグラフと最大最小の問題ですが、解の配置(2次方程式の解が指定範囲内にある条件を考える問題)もからんでいるので、やや高レベルの問題です。計算が簡単になるように数値が選ばれていて、よく勉強している実力派の人には何でもなかったと思います。ですが、標準的な受験生には厳しかったのでは?a,b,cの値や相互関係を適切にあてはめていかないと、時間をムダにする、という面もあります。第3問は、平面図形、三角比の問題です。私は、昨年の第3問の方が簡単だと思うのですが、今年の方が簡単という声もあるようです。この問題の前半は、余弦定理の式を2つ書いて、四角形の対角線を求める、という、よく見かけるタイプの問題で、この問題を試験会場で初めて見た、というのだったら、ハッキリ言って勉強不足です。これくらいの準備もなくセンター試験に臨む、というのであれば、大学に進学しても、就職活動で必ず苦労することになります。基本的なことだけでも、しっかり勉強しておくことが大切だということを肝に銘じてください。後半は、円の半径を求めたときに、辺BCが円の直径になっていることに気づけるか、また、気づけたとして、それを表す図を描けたか、ということが勝負の分かれ目です。ていねいに図を描き、図を見ながら進めて行けば何でもない問題なのですが、問題文の方に注意が行ってしまうと、ハマってしまうでしょう。こうした点は、日頃の習慣が影響します。ふだんから図を描いて考えるクセがついていれば、三角形の相似、方べきの定理、円周角の定理を使って難なく答えられるはずの問題です。第4問は、確率の問題です。計算が大変にならないように、序盤のミスで全滅してしまわないように、という配慮がなされています。各設問の相互関係が私にもよくつかめませんが、反復試行の考え方がマスターできていれば、昨年の第4問よりは取り組みやすかったと思います。全般的に、数学をしっかり勉強した人には取り組みやすく、当てずっぽうでは正解できないように工夫された問題になっています。実力差が如実に表れるのではないでしょうか?本ウェブサイトでも指摘してきましたが、過去、数学の試験と言うよりも注意力の試験ではないか、と、言いたくなるような問題が多かったことに対する改善のあとが見られます。繰り返しになりますが、滑らない砂を探す、などということではなく、しっかり勉強をしておくことが、センター数学の最善の対策です。追記(1月23日)大学入試センターの中間集計では、平均点は65.96点で予想外の高さです。問題のレベルよりも、計算の大変さで決まっている、ということのようです。大学入試問題研究サイト
2011.01.16
コメント(0)
-
未来の参考書
CFV21ウェブサイト(http://www.cfv21.com/)が目指しているものについて書いておこうと思います。CFV21が目指しているものは、一言で言えば、双方向参考書、未来志向の参考書、ということになると思います。既存の参考書では、解説中の式変形や論理展開の中に理解できない部分があっても、読者は質問もできずにうろたえることになります。自分で解決できないと、結局、学校や塾の先生に聞くことになると思いますが、先生でも、いきなり式変形の途中を聞かれても即座に返答できるわけではなく、自分でも計算してみて、どういうことなのか確認しなくてはいけません。生徒が理解できないほどのことなので、先生が考えてもやはり首をひねるようなことが多く、この間に、質問していた生徒の方は、じれてしまうことになります。やはり、正確を期するのには、その解答を書いた人自身が、どういうねらいで式変形をしているのか、返答するのがベストです。ですが、読者が質問のハガキを出版社に送っても、その質問が著作者のところに届くのには時間がかかります。これでは、参考書の読者は、参考書内に不明な点があっても、放置してしまうことになりかねません。参考書の記述中に不明な点が出てきた場合に、即座に質問できるシステムが必要なのです。参考書の執筆者から学ぶ人への一方通行ではなく、学ぶ人から参考書執筆者へのアクセスを可能にするものはインターネットです。参考書ごとにホームページがあって、そこに質問を受ける窓口が用意されていて、読者が疑問点を書き込むと、せめて一日以内くらいに返答が書かれる、というのが、参考書に望まれることです。これを現実に実践しているのが、CFV21ウェブサイトです。CFV21の会員になって頂ければ、印刷物の形ではありませんが、教材CDROMを会員にお送りしています。会員がCFV21のウェブサイトの内容に関して質問を送ると、ウェブサイトに返事が書かれます(例えば、こちら)。回答に納得がいかなければ、会員は何度でも再質問ができます。ウェブ化することにより、参考書が双方向になっているのです。CFV21ウェブサイトでは、基礎事項に関して逐一説明ページを作り、入試問題の解答ページなどから参照できるようにしてあります。基礎事項に関して疑問が生じても、索引など引くことなく、即座に基礎事項へのリンク先に飛ぶことができます。こうしたページを各参考書ごと、あるいは、出版社ごとに用意すれば、基礎事項を忘れていても即座に調べることができるし、その場で基礎事項の復習をすることもできて、時間の節約とともに、学習効果は絶大です。対象を参考書購入者に限りたければ、ウェブサイトにアクセス制限をかけることも容易です。最近は、レンタル・サーバーの価格も安く、見た目に凝らなければ、ウェブサイト運営費を極めて低く抑えることも可能です。参考書のウェブ化は、私が自分自身でやるよりも、本当は、東京出版や数研出版のような大手出版社、あるいは、東進ハイスクールのような先進的なことに熱意のある予備校が、数学物理学教育の専門家の力を借りて手がけるべきかも知れない、と、思います。ですが、雑誌「大学への数学」編集部にも、何度も提案していますが、ウェブ化については、全く相手にされていない状況で残念に思っています。明日の日本を担う優れた人材を養成するために、参考書をインターネットを利用して双方向化することは必須です。恐らく、インドや中国では既に研究も進んでいるのではないかと思います。日本が、インドや中国の後塵を拝する事態になって良いのでしょうか?昨年は関孝和没後300年であったのにもかかわらず、和算関連の本は見向きもされず、インド人の数学の本が書店に平積みされていて、日本人のプライドというものはなくなってしまったのでしょうか?出版社の方でこちらをご覧の方、もし、未来志向の参考書を制作するのであれば、ぜひ、cfv21にお声かけください。参考書を執筆するほどの余力はありませんが、ウェブ制作関係においては、幾多のご提案、また、お手伝いができると思います。大学入試問題研究サイト
2009.05.11
コメント(0)
-
CFV21での学習の進め方
一つ前の日記で、CFV21の理念について書いておきました。きょうは、こちらをご覧の高校生、受験生の皆さまに、CFV21を利用した数学・物理の勉強の進め方について書いておきます。一つ前の日記にも書いたように、CFV21では、会員の自発的努力をお願いしています。夢や希望をしっかりもって自発的に頑張る、ということは、医者の家に生まれてしまったから嫌でも医者になるしかない、勉強しろ勉強しろと怒鳴られてうるさいから勉強する、というのとは全然違います。自分の目的を実現するために、あるいは、今やっている勉強そのものが自分の目的につながるからこそ、受験準備に励むわけです。従って、もしあなたが、将来展望もなく、漠然とした気持ちで、このブログを眺めているのであれば、まず最初にすることは、自分の将来はどうなるのか?自分に似合った仕事は何なのか、まずは、夢や希望を探すことです。自分がやっていて楽しいこと、夢中になれること、好きなこと、自分の性格に適していること、関心を持っていること、そうしたものを真剣に考えてみてください。それとともに、日本社会が明日の世代に求めているものを考えてみてください。それができるだけマッチングするように、自分の将来設計を立ててみてください。わざわざ本を買わなくても、図書館に行けばいろいろな職業について、どういう基礎知識が必要か、大学で何を学んでおけばよいか、道案内してくれる本がいろいろあります。受験準備への意欲、というものは、そうした将来展望から湧いてくるものです。CFV21では、あなたの学力をつけるために必要となるもの以外の一切のムダを省いています。きれいな教室も豪華なパンフもありません。それゆえの3ヵ月3千円の会費になっています。高校生の小遣いでも大丈夫、という会費設定にしました。CFV21を利用して受験準備を進めて行くためには、パソコンが必須です。インターネットとEメールができさえすれば、5万円くらいで売られているマシンで充分です。インターネットのプロバイダ契約(光フレッツがよいですが、ADSLでも充分です)も必要になります。できれば、質問や答案を送るのに、スキャナかデジカメがあると良いです。一番安いもので充分です。質問を画像ファイルとして入力するために、WindowsのPAINTで、直接、文字を画像入力するのであれば、タブレットがあるとなお便利です(マウスで文字入力するのはきついです)。まずは、こちらまで、メールを送ってください。折り返し、ご案内のメールを差し上げます。頂いたメール・アドレスは他目的には絶対に使わないことをお約束致します。できれば、勉強の進捗状況を見て頂くために、おうちの方のEメール・アドレスにして頂くのが良いと思います。3ヵ月分の会費を振り込んで頂くと入会になり、こちらから、教材CDの最新版をお送りします。教材内容はホームページ上にも公開されていますが、一々ダウンロードするのでは大変です。また、教材CDでは関連事項のリンクも貼られていてとても便利です。ぜひ、入会して頂いて、教材CDをご利用ください。教材CDが届いたら、数学・物理について、高校の範囲のどこでも良いので、教材CD内の基礎事項、入試問題(通常のHTMLファイルになっています)をインターネット・エクスプローラで閲覧してください。疑問点が湧くときには、即、質問メールを送ってください。数式は、「2a分のマイナスbプラスマイナスルートbの2乗マイナス4ac」「(-b±sqrt(b^2-4ac))/(2a)」というような書き方で充分わかります。難しくてわからない、ということだけでなく、ベクトルにはなぜ上に矢印をつけるのか、というような基本的なこと、恥ずかしくて学校の先生にも聞けないようなことでも勇気を出して質問をしてください。納得がいくまで説明します。また、教材CDに掲載されている入試問題を解いて、その答案を送って頂ければ、添削をして返送します。できていないところがあれば、ヒントを書いて返送します。自力で完全に近い解答になるまで何往復でもします。点数をつけておしまい、ということにはしません。もし、教材CDに掲載されている問題を見て、全く解けそうもない、という問題があれば、素直に、「全然わかりません」とEメールしてきてください。どのようにとっかかりをつかむのかを、各会員にふさわしい考え方で、お伝えします。また、現時点では、頂く質問が非常に少ないので、当面は、各学校で配布される問題集や、プリントの問題であっても、問題と自分で作成した解答の両方を送って頂ければ添削するように致します。ただし、学校の宿題を代わりに解いておいてください、というようなものはお受けしません。代わりに解いてしまうのでは、会員の学力向上にはつながらないからです。あくまで山登りをするのは会員諸氏の役目、私の役目は道案内することです。質問に対しては、回答で数式を必要とするものは、ホームページ:http://www.cfv21.com上にアップして、そのURLをメールにてお伝えしますが、個人情報を含むようなご質問、ご相談については、Eメールのみで回答致します。高い授業料を支払って塾通いするのも、親切なケアを受けることができてよいのですが、お金を使わなくても、自分の足で歩き、自力で調べ、自分の頭で考えることによって、最難関の大学を受験できるだけの高い学力をつけることは充分に可能です。今の自分では、大学に行くことさえどうか、というような方でも、早慶理科大などの難関私大に、一年頑張れば充分に届きます。皆さんからの積極的なアクセスをお待ちしています。大学入試問題研究サイト
2009.05.06
コメント(0)
-
CFV21の理念について
一年ぶりに、本ブログを再開します。再開するに当たり、理工系大学入試支援ウェブサイトCFV21の理念を再確認しておこうと思います。少子高齢化、食糧自給率の低下、巨額の国家財政赤字など、日本社会の現状を見るに、日本の将来を考えるとどうしても暗い気持ちになってしまいます。明日の日本を支える有力な産業も見えては来ません。また、経済格差の拡大が教育格差にもつながり、経済的弱者の子弟が経済的理由で大学進学を諦めなければいけない、というような話も聞かれるようになりました。一部の高校では、授業料滞納のある生徒を卒業させない、というようなニュースも見ます。こうした時に、日本人の叡智を結集すれば何とかなる、というような楽観論や、日本人は農業をやっていれば良いのだ、というような、世界情勢を無視した後ろ向きの議論では、私は、日本を救うことはできないと思います。やはり、戦後から'80年代まで日本を強力に牽引してきた「科学技術立国日本」の姿を再生する以外に、狭い上に山がちで平野が少ない国土に一億人以上がひしめき、有力な鉱物資源を産出しない日本の将来はあり得ないのです。翻って、明日の日本を担う人材を育成すべき教育の状況がどうか、と、言うと、これまた、暗澹とした気分にさせられます。ようやく、'90年代に文科省がお人好し日本人に押しつけた「ゆとり教育」が見直され始めました。しかしながら、改訂された学習指導要領を見る限り、'80年代以前の先進的なカリキュラムにまで戻ってはいません。しかも、経済的困窮者の子弟は有能であっても高等教育の機会を与えられず、みすみす人材の損失を招く、という現状に至っているのです。ですが、果たして、経済格差は教育格差に直結するのでしょうか?本当に、教育にはカネがかかるのでしょうか?理工系大学入試支援ウェブサイトCFV21では、ゼロからの挑戦を旗印に、難関大学挑戦に必要なものは、 紙と鉛筆とチャレンジ精神を合言葉にしています。学力向上に必要なことは、高いお金を払って有名予備校の有名講師の授業を聞くことではありません。高い目標と意欲、強い意志をもって、自発的かつ積極的に学ぶことです。もちろん、経済的に恵まれた家庭の子弟が塾・予備校に通って親切なケアを受け、わかりやすくおもしろい授業を聞けば、難関大学入試において有利になるでしょう。ですが、それは有利になる、というだけであって、教育にカネをかけることは難関大学入試突破の必要十分条件ではないのです。むしろ、不利な状況におかれてもなお、ハングリー精神をもって歯を食いしばって頑張りきることこそが、難関大学入試突破の必要十分条件と言うべきです。理工系大学入試支援ウェブサイトCFV21では、経済格差が教育格差にはつながらない、ということを形をもって示すために、会費を3ヵ月3千円に抑えています。その分、教室も自習室も豪華なパンフもありません。会員の自発的学習を、Eメールで質問を受けることによりサポートすることで、費用をかけないように致しました。もちろん、会費を頂戴できれば塾・予備校にお通いの方でも、誠実にサポートさせて頂きます。経済的事情により夢や希望を諦めなければならない、と、お考えの高校生の皆さんに申し上げたい。経済力は教育成果とは関係ありません。あなたの意欲次第なのです。夢や希望をしっかり持ち続けて、初志貫徹しましょう。あなたの努力こそが日本を救う原動力となるのです。大学入試問題研究サイト
2009.05.05
コメント(2)
-
再開します
長らくお休みしていましたが、明日より、再開します。---------------大学入試問題研究サイト CFV21
2009.05.02
コメント(0)
-
訃報
「大学への数学」を発行している出版社、東京出版の社長の黒木正憲さんが、昨日、亡くなられたのだそうです。高校のときから、本当に長い間、お世話になりました。心より、ご冥福をお祈りいたします。
2008.05.05
コメント(0)
-
気分が乗らない時って、どうしてもあるよね
どうしても、勉強の方に気が向かない日、というか、気が向かない時期があります。文化祭の準備に打ち込んできて、文化祭が終わった後など、暫く放心状態になってしまったりします。頭の中ではやろう、やろうと思っているのだけれど、気持ちがついてこない、テレビでもついていると、別に興味があるわけでもないのに、押し流されるようにずっと見てしまう、というような時があります。そういう時がたまにはあってもいいのではないか、と、私は思いますが、一年中、ずーっと、ということになると、これは何とかしなくてはいけません。私は、これからの人に、朝から晩まで、数式だけが頭の中を駆けめぐっている、という、人間にはなって頂きたくはありません。もっと、情操豊かな、幅の広い人間になって頂きたいと思うのです。趣味にもいろいろなものがありますが、「音楽」というのは誰でも受け入れられるものだと思います。何を聞くか、ということになると、人それぞれだと思いますが、どうしても、勉強に気が向かないときには、いっそ、音楽をゆったりと聴いていたらどうか、と、私は思います。私は、高校の頃、ずっと、ヘビーメタルをヘッドフォンでガンガン鳴らして数学の問題を考えていました。本当に気分が乗ってくると、ヘビーメタルなのに、音が聞こえなくなるんですね。皆さまには、ヘビーメタルはあまりお勧めしませんが、ヒーリング系の音楽などいかがでしょうか?できれば、ボーカルの入らないものが勉強には向いていると思います。特に、日本語のボーカルはどうしても歌詞を聴いてしまうので、集中できなくなります。どうしても勉強の方に気が向かないとき、「勉強しよう」と自分に言い聞かせたりしないで、「音楽でも聴いていようか」と思うようにしたらどうか、と、思います。テレビは、目も取られてしまうので不可ですが、音楽なら耳を取られても、目と手は空いています。手が空くのだったら、コミック本を手に取らずに、教科書を手に取るのです。教科書の記述は難しくはありません。スンナリと目の中に入り込んでくれるでしょう。教科書の記述を目で追っているうちに、学校の先生の顔や、くだらないギャグや、友人の解答を思い出したりするでしょう。CD1枚聞く間に、あなたの頭は勉強モードに切り替わってくるはずです。最初は、学校で配布されるような基礎的な問題集をゆっくり解いてみることです。分野は何でも良いのです。計算練習の方が良いと思います。難しいものは全部飛ばして、手を動かせばさっと解答にたどりつくようなものを選んで、やっていくのです。調子が出てくると、今まで何となく眠気がしていたのが、目が冴えてきます。こうなったら、2時間で難問4題にチャレンジ、と目標を決めて、一気にスパートしましょう。無理に頑張ろうとしないで、自分の身の回りをだんだんと勉強の色に染めていく、調子が出てきたところで、一気に集中して頑張る、というようにしましょう。これが、入試会場で、120分~150分の制限時間の間に、一気集中で実力を出し切れるようにする秘訣です。大学入試問題研究サイト
2008.04.27
コメント(0)
-
線形計画法を追加しました
線形計画法が抜けているというご指摘を頂きました。図形と方程式の最後のところに線形計画法付け加えておきました。東大、東工大では、線形計画法が出題されるときでも、他の大きな課題の付け足しでちょこっと使う、という程度のことが多いので、以外と盲点の分野です。東工大では、'98年前期[1]にかなり手の込んだ問題が出ていますが、それ以外では、大きく取り上げられてはいません。実用的な話題で、最適計画を立てるような問題だと、意外とできが悪いのではないかと思います。こちらをご覧の方は、学校で配布される問題集で充分なので、体験しておいてください。今年の京大理系前期乙[6]も虚をつくような問題でした。過去問をていねいに見ておくのも大切なのですが、この10年間。あまり見ないな、という分野は、「出題されない分野」なのではなく、出題の可能性が高い分野だと思ってください。大学入試問題研究サイト
2008.04.24
コメント(0)
-
関孝和没後300年記念懸賞問題
慶大理工数学'08年[B1]の掲載が遅れてしまいました。解答の中にも書きましたが、この問題は、ベルヌーイ数に関連する問題です。ベルヌーイ数は、スイス人の数学者ヤコブ・ベルヌーイが発見した数列とされていましたが、江戸時代の和算家、関孝和が、ほぼ同一時期に、全く独立に同様の研究を行い、書物に表しているのだそうです(詳細は、日本数学協会のホームページを参照してください)。日本数学会では、「ベルヌーイ数」ではなく、「関・ベルヌーイ数」と呼ぶべきだ、と、言っています。2008年は、関孝和没後300年に当たるのですが、それにちなんで、慶大の先生が、ベルヌーイ数に関連する問題を出題してみようと思ったのではないかと推測します。日本数学協会では、「関孝和没後300年記念懸賞問題」として、関・ベルヌーイ数に関する考察と証明を行う問題を出しているので、我こそは、と、思う方は、ぜひチャレンジしてみましょう。6月30日が締め切りだそうです。詳細は、日本数学会のホームページを参照してください。大学入試問題研究サイト
2008.04.23
コメント(0)
-
自分のスタイルにこだわるべきか?
自分のスタイルにこだわることが大切だ、と、よく言われます。しかしながら、大学入試の受験勉強では、こうした凝り固まった考え方は危険です。私が思うに、勉強のスタイルを固めることができるのは、大学に進学して研究室に入り、専門的な研究に打ち込むようになってからです。CFV21を利用しなくても、既に、高いお金をかけて塾・予備校に通っている、という方も多いと思いますが、そういう方にこそ、むしろ、もっと、柔軟な考え方をするべきだ、と、申し上げたいと思います。塾・予備校に通っても、特に、有名な講師の場合には強いクセがあって、習う側が自分のスタイルにこだわるのであれば、どんなに素晴らしい授業を受けても、まず、得るものはないと言ってよいと思います。やはり、塾・予備校を活かすのであれば、その講師のクセに合わせて、勉強のスタイルを変えるべきです。思いやりのある講師なら、勉強方法の指示もしっかりするはずです。ノートの取り方から、予習・復習の仕方、問題集の選び方、使い方に至るまで、その指示に従って勉強を進めるのでなければ、実力が伸びるはずがないのです。特に、私が心配するのは、「自分のスタイル」と高校生が言う勉強法が、暗記に走る勉強法、とにかく長時間やることを自己目的化する勉強法であることが多い、ということです。睡眠時間・健康を犠牲にしてまで机に向かって、記憶に頼り、全パターンを体験することを追及することが、大学に進学してから、あるいは、社会に出てから役に立つのであれば、それも良いかも知れません。ですが、円周率を何万桁も暗記すれば褒めてもらえるかも知れませんが、実際には、暗記した知識は、大学進学後には、ほとんど役に立ちません。Googleで検索してしまえば、あらかたの知識を調べ上げることができてしまうのです。むしろ、高校では、Googleでいかにうまく有益な情報を抽出するか、ということのトレーニングをするべきです。もちろん、英単語・英熟語、数学の基礎事項、基本的解法などはしっかり暗記するべきですが、大学入試に必要なレベルのものを暗記するのであれば、睡眠時間を犠牲にするほどにはならないはずです。難関大学にいとも簡単に合格する先輩を見て、頭の構造が違うのかなあ、と、思うかも知れませんが、頭の構造が違うのではなく、何を記憶しているかが違うのです。こちらをご覧のあなたが、学校から家まで帰ってくるとき、どのように帰ってくるでしょうか?帰り道に視野に入ってくるものを全て暗記しているでしょうか?信号を左に曲がって、次に右に曲がるまでの間に、何件の家があって、誰さんと誰さんの表札が出ていて、駐車場のある家にはどんな色の自動車が止まっていて、ナンバーはいくつ、マンションのタイルは何枚貼られていて、家の庭にどんな花が咲いているか、などと、細かく覚えているわけではありません。家に帰り着くのに必要な情報は思いのほか少ないのです。CFV21においても、塾・予備校においても、大学入試に必要な情報を効率的に選択する方法についてアドバイスを送っているので、自分のスタイルに合わないから、せっかくのアドバイスを受け入れない、というのであれば、自動車のナンバーばかりを暗記して家に帰るのに道を間違えるということになってしまいかねません。大学に進学して、自分の専攻分野が見つかるまでは、スタイルを固定せずに、いろいろな人のアドバイスを柔軟に受け入れるようにして欲しいと思います。大学入試問題研究サイト
2008.04.22
コメント(0)
-
そもそも、何がわからないかがわからない
物理を勉強するのに当たって、質問をしてください、と言われる以前に、「何がわからないか」が、そもそもわからない、というご意見を頂いています。物理という科目は、物体がどのように動くのか、自動車を設計するときに、どのようなエンジンにするとどれくらいの加速度が出るのか、とか、携帯電話の電波が街頭のアンテナに届くようにするためには、どれくらいの電流を流せばよいのか、というようなことを、あらかじめ計算して求めておく方法を学ぶ科目です。学校で習ったことを使って、物体の運動や電流を計算してみればよいのです。友達同志でキャッチボールをするときに、どのくらいの角度でどのくらいの勢いで投げると、どの辺まで飛ぶかを調べて、計算の結果と比べてみましょう。水平方向の移動距離とボールの移動時間と投げ上げた角度がわかれば、ボールの初速度がわかります。もちろん、空気の抵抗もあるのですが、最高点が学校の校舎の何階のどの辺だったか、ということを計算結果と比較してみることができます。抵抗を直列接続したり、並列接続したりして、乾電池から流れ出す電流がどれくらいになるか、テスターなどの学校備え付けの計測器を借りて測定し、計算結果と比べてみましょう。あるいは、学校の授業で実験を行ってレポート作成の宿題が出たときには、実験結果を計算によって確かめることができるか調べてみましょう。実際に計算をしてみようとすると、なかなか実測に合わなかったり、計算方法がわからなかったりします。教科書を読んでも、うまく計算ができなければ、質問をしてみてください。実測に合わない理由については、摩擦力などの想定外の力の寄与が大きいというようなこともあるので、状況がつかめないと、必ずしもお答えできないかも知れませんが、疑問点を整理することはできます。意欲溢れる方の場合には、Challenge from the VOIDサイトに掲載されている、入試問題に挑戦してみましょう。最初からスイスイ解答できてしまう、というようなわけには行かないと思います。そのときには、つまづいたところで、気軽に質問メールを送ってきてください。大学入試問題研究サイト
2008.04.21
コメント(0)
-
物理での微積の取り扱いについて
CFV21には微積がどんどん出てくるけれども、学校で物理に微積は必要ないと言われた、というご意見を頂きましたので、お答えしておきます。高校物理の教科書は確かに微積色を薄めて書かれています。いろいろな大学の入試問題を見ていても、微積を使わずに答える問題ばかりです。少なくとも、大学入試で物理の問題を解くためには、微積は必要ないと言っても良いと思います。私も、敢えて、微積を使って問題を考えようとは思いません。しかしながら、近似計算を必要とする問題などで、近似の仕方が非常に難しく、微分してしまえば、数学IIIに出てくる程度の微分計算ですんでしまう問題なのに、なぜ、敢えて近似計算でやらなければいけないのか、と、思うような入試問題も散見されるのです。電磁誘導の法則を適用する問題では、私は、磁束を時間微分して起電力を計算してしまう方が簡単だと思います。ことしの、東大物理'08年前期[3]も、微分方程式と思ってしまえば簡単なのに、高校の範囲で考えようとすると工夫が必要な問題です。東大物理では、75分で3問解かないといけないので、試行錯誤している時間的余裕がありません。こういう問題では、微積は使わない、などと、決めてしまわない方が良いと、私は思います。それと、物理学そのものは、ニュートンが「力学」を作ったときから、微積分学とともに、発展してきているのです。大学に進んでからの話ですが、物理学を微積なしに考えるのは、ナンセンスです。ですが、一応、ご忠告を申し上げておくと、必要もないのに、微積を振り回さない方が良いと私は思います。大学の入試問題は、微積を使わなくても解答可能なように配慮されているのです。「速度を求めよ」という問題で、微積の方に頭が向いてしまうと、エネルギー保存を考えつかない、というようなことも起こりえます。私の印象では、微積を適用するよりも、エネルギーで考える方が遙かにラクな問題の方が、圧倒的に多いと思います。大学入試問題研究サイト
2008.04.17
コメント(0)
-
さあ、チャレンジしてみよう
新しいことにチャレンジするとき、誰でも大きな抵抗感を感じます。何も無理しなくても、既存の路線に乗っていれば、と、思ってしまいがちです。ですが、既存の路線が、よほど強力なものでない限り、今までやってきた方法で努力するだけなら誰でも努力するので、なかなか、期待する結果が、自分の思う通りに出てこなくて、気持ちが焦ってくることがあります。周囲の人も目に見える結果を求めたがるものです。従って、やはり、現状を打破してチャレンジすることが必要になるときがあるのです。無理なチャレンジをして、新しいステージへ駆け登ったとします。最初のうちは、ステージ上で活躍できることに快感があるかも知れません。でも、チャレンジが無理なものだと、やがて疲れて、強烈な倦怠感に襲われることになってしまうことがあるのです。また、それが予感できるからこそ、チャレンジには尻込みしたくなる、とも、言えます。チャレンジするときには、義務感を背負わずに、のんびりと無理をしないように、スモール・ステップで登って行くのが良いのです。いきなり、自分の環境をドラスチックに変化させてしまうのではなく、生活空間の10分の1ずつ入れ換えていくようにするのです。そして、結果を急がないことです。チャレンジの道をゆっくり歩く、ということは、なかなか結果は出ない、ということです。むしろ、道ばたの花やモニュメントの中に新しい発見をしながら、寄り道を楽しみながら歩いて行くべきでしょう。大学入試であれば、半年から1年、あるいは、東大でも2年もかけて準備すれば充分です。それくらいの道中であれば、道を急ぐ必要はないのです。Challenge from the VOIDのウェブ・サイトで言えば、自分の興味が向くところから開いて読んでいれば良いのです。こっちを読み、あっちを読み、としている間に、体質転換ができているのです。難関大学など自分には無関係、と、思わずに、なあんか、おもしろいことはないかな、という感覚で、最初は読んでいってもらえたら、気づいた時には、難関大学が手の届くところにあった、ということになると思います。大学入試問題研究サイト
2008.04.16
コメント(0)
-
難関大学への早道
高校生や、高校生のお父様、お母様とお話ししていて、感じることがあります。それは、必死に努力することによって、ハイレベルな学力がつき、東大・一橋大・東工大・京大のような難関大学にも合格できるはず、という勘違いをされている方が多いということです。趣味も運動も読書も余計なことはさておいて、全ての時間を受験勉強に回すくらいでなければ、難関大学には合格できない、と、思われている方が多いのです。ですが、茨城県のラグビーで有名な高校の生徒でしたが、高3の10月頃の時点で、花園を目指す(ラグビーは正月に全国大会があります)と言っていて、理科三類に合格した人がいました。今、神宮球場で行われている東京六大学野球で、東大は、ハンカチ王子・斉藤投手の早稲田大学にコテンパンにぶちのめされてしまいましたが、この試合に登場した灘高校から理科三類に合格した投手は、高校3年の夏まで、野球をしていたそうです。私の経験でも、東大のキャンパスを歩いていると、ショパンの名曲をサラサラと弾いてしまう人、理系なのに、高校のうちから社会学の本を読みふけっていた人、大道芸の達人、等々、高校の時に青春を謳歌していたような人が多いのです。そういう学生は、もともと頭の構造が違うんだ、と、おっしゃる方もいますが、東大の学生だからと言っても、早稲田や慶應や明治や法政の学生とどこも違いません。むしろ、早慶の学生の方が、知的な秀才が多いのではないでしょうか?ですが、司法試験や国家公務員試験のような試験になると、東大の学生が強いのです。私は、日本にとってそれが良いことだとは思えないのですけれども、それが現実です。一言で言ってしまうと、東大の学生で感じるのは、短時間に一気にズバっと仕事をやりきってしまうタイプが多いのです。短い時間に義務的な仕事をこなして、残りの時間は自分の好きなことに打ち込む、というタイプが多いのです。東大理系の数学や理科の試験時間は150分もあるので、思考の忍耐力も必要なのですが、最も重要なのは「集中力」のような気がします。東大の入試で闘うための「集中力」を磨くためには、生活時間の全てを受験勉強に注ぎ込む、という発想は、控えた方が良い、と、私は思います。長い時間をかけて勉強するクセをつけてしまうと、どうしても、短時間に一気に実力を出し切ることができなくなってしまうのです。難問題に当たったときに、次から次へと新しいアイデアをひねり出す、ということができなくなってしまうのです。むしろ、勉強時間は1日に4時間と決めたら、その間に一気に目標を仕上げ、あとは、部活動でもスポーツでも演劇でも映画でも、自分の趣味に打ち込むことの方が、東大の受験対策になるのです。むしろ、部活動や趣味や福祉ボランティア活動を通じて得られた異質な文化との出会いが、数学の難問で思いもかけないひらめきを生んだりするのです。東大の数学の入試問題は、年によっては全く平凡な問題ばかり並ぶ年もありましたが、このところ、重厚な問題を揃えてきています。高校の授業で得られた知識、あるいは、塾・予備校で教えてもらえるスーパー・テクニックなどを駆使しても、思いつけないような発想をする問題が、今年も出ています。高校で甲子園を目指して投球練習に打ち込んでいたときに、同じフォームで少しずつ握りをずらしてみたら、どういう球が投げられるか、と、練習していた投手が、入試の会場で、さっぱり意味不明な問題を眺めつつ、そういやあ、投球練習のときにちょっとずつずらしてみるなんてやってみたなあ、と、思いながら、条件を少しずつ動かしてみると、問題のカラクリに気づいてしまう、というようなことがあるのです。こうしたことは、必死の努力の結果でも、睡眠時間まで削って長時間勉強したことの成果でもありません。もっと幅広い人間的な経験、というようなところから湧いてくる発想です。そして、少子高齢化の日本をどうするのか、高齢者の医療問題をどう解決するのか、日本の科学技術をどう発展させてゆくのか、こういう難問題と真剣に取り組んでいく人材を養成するためには、スーパー・テクニックよりも、幅の広い発想法の方が重要になるのです。もちろん、東大の入試問題でも、高校の全範囲から出題されます。抜けのないように、しっかり勉強しておくことが必要不可欠なのは言うまでもないことです。だからと言って、高校3年間を、受験一本に絞って、それ以外のことをやるのは時間のムダと考えてしまうのは、難関大学入試に限っては大きな間違いです。短時間に一気に集中して成果を上げられるように勉強し、できる限り余暇の時間を作って、自分の趣味に合わせた活動をする、というのが、難関大学への早道なのです。大学入試問題研究サイト
2008.04.15
コメント(0)
-
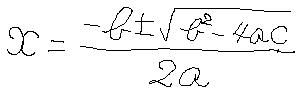
CFV21への質問方法について
CFV21では、会員になって頂くと、送って頂いた質問に、お答えいたします。会員になって頂いた方のために、当会への質問の方法について書いておきます。数学・物理の質問をする場合に最も困るのが数式の記述です。例えば、2次方程式の解の公式を書くのであれば、以下のように、Windowsのpaintのような画像ツールをを用いて、GIF形式、JPG形式、PNG形式のファイルを作成して頂くか、(ヘタな字でごめんなさい)x=2a分の(-b±ルート(bの2乗-4ac))というような話し言葉と同じ書き方で、数式を表現してください。BASICやC言語などの文法に則した記述にしようと思わなくても大丈夫です。無理に、特殊文字を使わずに、ふだん、読んでいるとおりに書いて頂ければ、充分にわかります。意味が取れなかった場合には、こちらからまた、お問い合わせのお返事を致します。画像ツールで数式の記述を書いて頂いた場合には、Eメールの添付ファイルとして送って頂ければOKです。心配だったら、添付ファイルをつけました、と、メール本文に書いておいてください。図やグラフなども、同じように、paintで簡単に絵を描いて添付ファイルで送ってください。その際に、字が汚いと恥ずかしい、とか、きれいに書かないと失礼だ、とか、笑われてしまわないか、とか、無用なご心配をなさらずに、わかりさえすればよい、というつもりで、気軽に質問を送るようにしましょう。CFV21では、読めるようになっていさえすれば、見栄えについてとやかく申し上げることはありません。なお、当会では、発行されている教科書をすべて集めて調べる、ということをやっているわけではないので、学校で使っている教科書の記述について疑問がある場合には、「教科書の何ページ」と書かないで、そこに書かれている言葉をまず書いて、どこがどうわからないかを、書くように心がけて下さい。不思議と、どこがどうわからないのか、と、思って質問を書いているうちに、わかってしまった、ということがあります。特に物理では、教科書の説明が、私が読んでいてもわかりづらいものが多々あります。CFV21ウェブサイトの基礎事項の説明を読んでも納得がいかない、あるいは、説明が抜けているようなことについては、どんどん質問を送ってきてください。数学・物理の勉強では、疑問に感じることを放置してしまうことが、大きな失敗や、勉強時間のムダにつながってしまいます。また、勉強を進める上で、いろいろと、悩みをお持ちの方も、お気軽にメールに書いてきてください。メールに書いて、話をしているうちに、それだけで気が晴れてくる、ということがあります。大学入試問題研究サイト
2008.04.14
コメント(0)
-
東工大'08年前期の物理について
東工大の'08年前期入試の物理の問題について書いておきます。今年は4題になりましたが、基本レベルはセンター試験に任せて、2次試験では、物理的思考力を試す第3問と第4問だけでよいのではないかと思われます。第1問、第2問でムダな時間を食って、第3問、第4問をじっくり考える時間がなくなったりしないように注意しないといけません。第1問は、レンズの基本問題です。センター試験と同じ問題だということで対象外となった設問がありますが、こういうことをしてしまうと受験生に予断を与えることになるので、私は構わず実施すべきだと思います。ですが、教科書の例題かと思うような問題で、出題意図がよくわかりません。第2問は、断熱変化の公式を求めて、気体がした仕事を内部エネルギーの減少分として求める問題で頻出パターンの問題です。4題になったので、このレベルになっているのだと思われますが、例年はもう少し味付けされています。第3問は、サイクロトロンと違って同心円で半径が増大するように加速するのではなく、加速後に円の中心がずれることに気づかないと題意がとれません。必ずしも問題文が親切とは言えませんが、じっくりと出題者の意図が理解できるまで問題を読みこなしてください。東工大では、物理の試験が現代文の読解力の試験を兼ねていると言っても良いのです。結局、問題文の図をよく見て、何が起きているか、ということをつかめるか、ということになります。また、この問題での交流の取り扱いは、干渉縞の考察と似たものがあります。教科書の基礎事項を物理的にしっかりと理解しておくことが、こうした問題を解くために必要不可欠です。第4問は、受験生にじっくり考えさせたい問題です。状況設定は簡単ですが、細かくエネルギー収支と摩擦力の関係を追って行く必要があります。感覚的に問題を眺めてしまうと、正解できません。東工大の名にふさわしい問題で、あくまで物理として、教科書の基礎事項に基づいて考える必要があります。一旦、右に行きすぎて、元に戻ってきても止まれずに行き過ぎる、ということが、2次方程式の解が出てくるか、ということをからめて考えるのは爽快です。第1問と第2問がやや余計なので、第3問と第4問の両方を完答するのは無理だと思いますが、どちらかはやりきりたいところです。受験生心理としては、どうしても、第1問と第2問を確実にものにして、第3問、第4問はできる範囲で、ということになってしまうので、今年の4題では、物理ではほとんど差がつかなかっただろうと思われます。大学入試問題研究サイト
2008.03.24
コメント(0)
-
東工大'08年前期の数学について
東工大の'08年前期入試の数学の問題について書いておきます。よく練られていて、バランスよく受験生の実力を見ようという良質な問題が今年も並んでいます。東工大の入試で成功するためには、小手先の技術ではなく真の実力を磨くこと、それ以外にはない、ということです。第1問は、微積の計算問題です。東京理科大でよく見るようなややこしい計算問題です。近頃、受験生から「面倒くさい」という声をよく聞くのですが、そうした意識への警告と言える問題だと思います。面倒でも地道にコツコツと確実に計算していくしかありません。研究者、技術者として最前線に立つためには、見かけの華々しさには踊らされない地道な努力が求められるのです。そうした素質も、入試問題では試されているのです。hlogh→0はほぼ自明ですが、時間的余裕があるのなら、証明を付けておく方が無難です。第2問は、はさみうちを利用する極限の問題で東工大では頻出のパターンです。a≠bとa=bとで場合分けが必要になるのも、東工大ではお決まりのパターンです。a=bの場合がなかなか難しいのですが、それをものともしない「大学への数学」4月号の解答は秀逸です。なかなか試験会場で思いつけるものではありませんが、よく、味わっておいて頂きたいと思います。なお、cfv21ウェブサイトにおいては、誰でも考えつけるどん臭い解法を心がけています。第3問は、コーシー・シュワルツの不等式(正しくは、コーシー・シュヴァルツの不等式と言うらしい)を思いつければ、10分少々で解答できてしまう、今年の東工大の問題の中では最も易しい問題なのですが、思いつけないと大変かも知れません。東工大の入試問題では、大学の教養課程くらいで使う教科書や副読本のようなところからそのまま焼き直して作ってくる問題を見かけます。この問題もその一つと言えると思います。高校2年生くらいまでにさっさと教科書の基本事項をマスターしておいて、高3では、受験勉強の息抜きに、専門的な本にも目を通しておくと良いのです。大学では、こんなこともやるんだ、それで、高校で2次関数だの、数列だのやるんだな、ということが納得できれば、受験勉強にもなお身が入るというものです。第4問は、回転変換と楕円の融合問題です。回転変換を使うと計算が膨大になることもありますが、ここでは、回転で考える方が良さそうです(偶然かも知れませんが)。こうした問題では、技巧を弄するよりも、まずは、最もシンプルな解法で行き詰まるまでやってみて、対処不能になってから、別の工夫を考える方が良いと思います。今年の問題の中では、最も取り組み易い問題です。全体を通して、第3問をコーシー・シュワルツであっさりと片付けた受験生は非常に有利だったと思います。ですが、第3問ではまってしまったとしても、第1問、第4問を完全解答し、第2問を半解すれば、数学としては充分に合格ラインだと思います。大学入試問題研究サイト
2008.03.23
コメント(0)
-
東大'08年前期の物理について
東大の'08年前期入試の物理の問題について書いておきます。数学と比較すると、うなって考え込むような問題はありません。昨年の問題と比較しても、基本的で軽量級の問題ですが、今年の問題は分量が多いので、かなりスピードを上げて解かないと、もう一科目に取り組む時間がなくなります。昨年が少々無理だった、という反省があるのかも知れません。第1問は、力学の基本的な問題です。これとよく似た問題が'80年代にも出ていたように思います。教科書をしっかり理解しておけば充分に正解可能でしょう。今年、地方の進学校の合格者数が多かったのは、こうした問題のためだろうと思います。授業中に、塾なんて行かなくても基本的なことをやっておけば東京の受験生に負けないんだ、と言っている地方高校の先生の顔が目に浮かぶようです。ですが、来年はまた昨年の第1問のような問題に戻るかも知れないので油断なきように。第2問は、ネオンランプの電流-電圧特性などが出てくるので、一見して難問かと思いますが、やっていくと標準的なコンデンサーの問題だとわかります。非直線抵抗の技巧のようなものも必要ありません。この問題も処理能力が問われている問題で、物理的な検討をするような部分はありません。ただ、やることは多いので、時間的には苦しいかも知れません。第3問は、ちょっと目新しい気体の問題です。大気や海中の状況を研究している研究者が日常的にやっている計算を出題したものだと思われますが、やはり、物理的に思索するような部分はなく、Iの(5)の計算方法が問題になる程度です。c(0)-c(L)という形から、dc/dzをLから0まで積分する定積分を思い浮かべれば良いでしょう。容器内の気体のモル数がnという条件をうまく使うところがポイントでしょうか。恐らく、この問題は、元々単振動するところまでだったのを、時間的に厳しすぎるというところで、切り詰めたのだろうと思います。全体を通して、数学のよく練られた問題と比べると、ちょっと物足りない、もっと分量を減らして、物理的な検討を必要とする問題を工夫して欲しい、と、私は思います。ただ、昨年はかなり重量級の問題だったので、毎年、今年のようなわけではなく、東大志望の方は、身の回りの自然現象や、学校で行う実験の考察について、じっくりていねい考えることを心がけて欲しいと思います。大学入試問題研究サイト
2008.03.22
コメント(0)
-
東大理系'08年前期の数学について
東大理系の'08年前期入試の数学の問題を解いてみました。最近、東大も以前に比べると易しめでしたが、今年は、やや、東大らしい本格的な気骨ある問題になったような気がします。しかしながら、無理な難問が多かった'90年頃に比べると、まだ、易しい感じがします。150分という制限時間のある入試問題としては、この程度で止めておかないと、能力と意欲のある学生を選抜するという目的が達成されなくなってしまうかも知れません。今年の問題は、後ろに行くほど難度が高くなってくるので、第1問から順番に丁寧に見ていくのが良いと思います。第1問は、1次変換の難問かと思うとそうでもなく、最初の3本の直線l0,l1,l2の交点を調べて、いずれも点(-1,2)を通ることに気づいてしまえば、あとは、東大では頻出の3項間漸化式を解くだけの問題になってしまいます。解答が無限角形の領域になるはずがないと、最初から決めつけてしまうべきかも知れません。第2問は、状態の遷移を図に書いて考えれば、容易に解答できる確率の問題です。東大の確率は、漸化式を立てる問題になっていて漸化式がうまく作れないときには難問であることがありますが、比較的取り組みやすい問題であることが多いように思います。この問題は、白黒の区別がないこと、「初めて」という言葉があるので、一度、同じ色になってしまえば、そこでゲーム終了と考えて良いこと、を、考え合わせれば、計算ミス、勘違いが怖いだけの問題です。第3問も、ちょっと見た目にはどっきりさせられますが、正二十面体、というならともかく、正八面体を真上から見た図を描けというのが強力なヒントになっていて、ていねいに図を描けば容易な問題です。ただ、過去には、本当に考え込んでしまうような空間図形の難問も出題されているので、甘く見ないようにして欲しいと思います。この問題は、G1G2の周りに正八面体を回転すると言っても、辺を回転させるだけなので、ねじれの位置にある直線を回転させて双曲面になる問題をやったことがあれば、定型問題です。かつて、雑誌「大学への数学」に投稿したことがありますが、'98年東工大後期[2]のような、円筒を斜めに回転させるとどうなるか、という問題では大変なことになります。第4問も、一度でも経験したことのある人には一本道の定型問題なのですが、初体験だと、解と係数の関係の利用に気がつけなかったり、相加平均・相乗平均の関係がうまく適用できないときに、行き詰まってしまい易いかも知れません。東大では、発想力の問題ばかりでなく、よく勉強してきた受験生に報いようという趣旨の問題も毎年必ず出題されています。必ずしも易問ではありませんが、このタイプの問題を落とさないことが合格の秘訣です。第5問は、(1)はすぐに数学的帰納法に気づけると思いますが、(2)は苦労すると思います。要は、5のべき乗を4で割ると余りはいくつか、という問題の応用問題で、二項定理の適用で解決できる問題ですが、そこに行くまでの道のりが長いので、証明の構想を練ったり、別のうまい証明方法を考えている間にどんどん時間が経ってしまいます。第1問~第4問までをほぼ完答している自信があればじっくり取り込んでも良いですが、そうでなければ、他の問題に時間を割くべきです。しかしながら、問題としてはいかにも東大らしいよく考えられた問題で、前提知識も不要、数学のおもしろさを味わえる問題です。東大志望者には時間をかけてじっくりと楽しみながら考えてみて欲しいと思います。第6問は、絶対に最初に手がけてはいけません。時間的余裕のあるうちだと、微分して増減や凹凸を調べたくなりますが、グラフの概形が見えてこないため、面積計算にはつながらないことに時間をムダに費やして焦ることになります。時間的にせっぱ詰まった状況で解けば、数値代入して通過点を求め、グラフのおよその姿をつかんで積分計算へと進むことになるでしょう。いかにも受験技巧を使うように見える設定にしておいて、実は単純素朴に取り扱った方がうまく行く、という、アンチ受験技巧的な落とし穴問題も、東大ではよく見られるのです。ことしは、末尾の問題なので泣いた受験生は少ないと思いますが、落とし穴問題が第1問に来ていることもあるので、充分に注意してください。この問題は、面積計算もややこしくて、うまく整理して計算を進めないと手こずります。難問というわけではありませんが、今年の問題の中では、一番得点しづらい問題です。この6題だと、第1問~第4問の答案をしっかり書いて、そのうち3題をほぼ完答し、第5問(1)ができていれば合格ラインだと思います。大学入試問題研究サイト
2008.02.28
コメント(2)
-
高校物理教科書はこれで良いのか
先ほど、プロバイダーにトラブルがあったそうで、しばらく、FC2ブログの数式表示ができませんでした。楽天ブログでお詫びしても仕方ありませんが、ご面倒をおかけしたと思います。こちらでお詫び申し上げます。以前にも数ヶ月サーバーがダウンしているのに気付かず、数式表示ができなくなっていたことがありましたが、今回は、プロバイダーの方の問題で、既に復旧しています。17日の午前2時~午前6時にも、プロバイダー側のメール・サーバーの交換作業があるのだそうで、数式表示ができなくなります。あらかじめ、ご了解ください。この辺の問題は、数式表示で苦し紛れのことをやっているためであり、FC2ブログ様の問題ではないので、この点についてもご了解をお願いいたします。ライブドア・ブログは優れた工夫を行っていて高い技術力を感じさせますが、ライブドア・ブログはサイト内で完結しているので問題はありません。さて、「電磁波」に関する項目を大学入試問題研究サイトにアップ致しましたが、高校物理の現行教科書の問題が、「電磁波」の項目に集約されているように思いました。現行教科書は、「ゆとり教育」として制作されているはずなのに、どこにも「ゆとり」のない、知識詰め込み型教科書になっている、という問題点の他に、原理にさかのぼらず、現象だけ列記していくという側面を持つことも問題だと私は思うのです。ウェブサイトでどういう風に記述するか、どうしても悩んでしまいます。もし、こちらをご覧の教育関係者で発言力のある方がいらっしゃいましたら、ぜひ、高校物理の教科書の「電磁波」の記述はこれで良いのか、確かに、図や挿絵はきれいですが、内容的にこれで良いのか、よく、ご検討頂きたいと思います。「電磁波」の発生のメカニズムを一般的レベルの高校生に定性的に説明するのは、私は無理だと思います。高校の範囲としては、もっと基本的な概括的な説明に止めるのでよいのではないでしょうか?世の中に、定性的に説明することが分かり易く説明することだと勘違いしている人が多いのですが、物理法則は、計算して示すのがもっとも分かり易いのです。手許に、東京書籍の「物理II」という教科書があるのですが、この教科書の電磁波発生の説明は、私にもちんぷんかんぷんです。図も掲載されていますが、何のことかサッパリわかりません。電磁波の伝播速度(光速)の導出も行っていますが、私には、どうしてこれで、電磁波の伝播速度になるのか理解できません。この記述で、本当に高校生が、電磁波発生のメカニズムを理解できるのでしょうか?大学入試問題研究サイトにおいては、理屈をうまく説明しないままでおくのでは、高校生に物理をオカルトだと思わせることになってしまうので、マクスウェルの方程式までさかのぼることにしました。電磁波の伝播速度は、マクスウェルの方程式から導出すれば、単なる計算の問題でしかありません。この方がよほど単純明快です(ベクトル解析を勉強すればの話ですが)。このために、偏微分や重積分、ベクトル解析まで記述せねばならず、大変なことになってしまいました。私としては、「電磁波」の発生のメカニズムや偏波や熱放射など教科書で取り扱うべきではないと思います。どうしても、高校の授業で触れてもらいたいのなら、先生向けの解説書にだけ入れるべきです。先生に、「教科書に出ていないけれど、電磁波って実は、こうなっていて、大学の時、オレはこういう風に勉強した」というような話をしてもらえれば良いと思います。物理の教科書で非常に気になるのが、物理学者の生年や没年を入れていることです。物の性質を理解する「物理」という学問ではなく、「物理学史」にしてしまいたいのでしょうか?どうしても入れるのなら、巻末に「科学の歩み」などとして年表をつけておけばよいと私は思います。科学技術者ではなく、評論家を養成しても、日本はやっていけません。高校生が、定期試験の頃になると、意味不明な電磁波発生のメカニズムはさておいて、マクスウェルやファラデーやヘルツの生年や没年の暗記に走るのかと思うと、暗澹とした気分になります。日本史教科書の沖縄戦の記述で日本中が大騒ぎになりましたが、ほんの数行の記述に過ぎません。物理の教科書の問題は、高校物理をどう教えるかというところにまで行きつく、日本史教科書以上の大問題だと私は思います。高校生が、習っている物理の先生の悪口を言うのをよく耳にするのですが、こんな教科書では、高校物理の先生が気の毒としか言いようがありません。大学入試問題研究サイト
2008.02.15
コメント(1)
-
センター試験の数学の問題を解いてみました
センター試験の、数学IAと数学IIBの問題を解いてみました。今年の問題も、これが、数学の能力を見るのに適切な問題だとは私にはとても思えません。まず、数学IAについて。第1問[1]は、台形の面積を立式して2次不等式を解くだけの問題で、計算ミスに注意するだけです。[2]は、必要条件、十分条件の問題で、難しくはありませんが、「かつ」、「または」と「否定」が組み合わされていて、論理の考え方が完璧に理解できていないと正解できない問題です。これは良い問題だと思います。第2問は、2次関数を平方完成し、グラフを考える問題ですが、グラフを描いて考えれば、難しくはありません。計算も面倒にならないように工夫されています。第3問は、図形の問題で、正弦定理、余弦定理、接弦角の定理、方べきの定理を扱う問題で、基礎事項をしっかりマスターできている人は、計算ミスに注意すればよい程度の問題。強いて言えば、EA,EC,EDの長さを考えるあたりで、見落としている条件がないか、はまらないように注意する程度です。この問題では、接弦角の定理や方べきの定理は記憶していなくても、三角形の相似を意識させるようになっているので、解けるはずです。第4問は、場合の数、確率の問題で、場合の検討抜けが怖い問題です。落ち着いて、全ての場合の確率の和が1になることを確認した上で期待値の計算をすれば良いのですが、解答欄に合わなくて困った受験生もいたことだろうと思います。全般的に見ると、易しい方の部類で、十分に検算をする余裕もあって、満点続出だろうと思います。平均点もかなり高いと思われます。数学IIBについて。まず、第1問[1]で問題文を見るなり、精神的動揺を起こしてしまった受験生がいただろうと思います。メアリー・ポピンズの「スーパー・カリフラジ・リスティック・イクスピアリ・ドウシャス」とか、「魔界転生」で天草四郎がつぶやく「エロイムエッサイム、エロイムエッサイム、我は求め訴えたり」(こんなの知っている受験はいませんね)とか、何かおまじないを念じて、正気を取り戻してから取り組むようにしたいものです。変な式ですが、変な部分は消去できるようになっているので、落ち着いてやれば、誘導がていねいで、難しいところはありません。[2]は、弧度法でラジアンの定義や扇形の面積を理解しているかを見る問題。こういう問題で思うのですが、a などという文字を使って計算させる意味が私にはどうしてもわかりません。題意を取り違えたり、途中の計算をミスして、試験中に悩んだ受験生も多いと思います。数学IIBの試験なのに、余弦定理を使わせるのも、私には賛成できません。最後に、正弦の周期を考えさせるところは、数学の力が出るので、なかなか良いと思います。第2問は、放物線の接線や、面積を求め、場合分けをした上で、面積の最小値を微分して求める問題。数学の実力を見るのであれば、もう少し単純素朴な状況設定の方が良いのではないかと私は思います。計算もかなり面倒です。もっとひどい年もありましたが。この辺は、センター試験向けにかなり計算練習を積み、検算の方法をしっかり習慣づけておかないと、試験中にトラブルになる問題です。数学の問題と言うよりも、注意力の問題。第3問は数列の問題です。センターとしては、こういう問題しか作れないのでしょうか?私は、もっと単純な問題で基礎的な力を確認するので充分だと思います。この問題も、完答は容易ではありませんが、面倒でも誘導通りに計算するだけで、考え込むようなところは全くありません。計算ミスに注意するだけです。第4問は空間ベクトルの問題ですが、この問題は、面倒な計算をさせないような工夫が為されていて、比較的よく練られた問題です。それでいて、共線条件などをよく理解していないと、途中で行き詰まります。ベクトルCPの大きさを求めるところがやや面倒ですが、これは仕方がないかも知れません。空間ベクトルでは、どうしてもこういう部分が出てきます。最後の方で、ベクトルCPが三角形と垂直、などと書いてあるので、途中の答がわかってしまったりします。逆に言うと、ここで、[ス] の枠がゼロでなければ、どこかミスしているということに気づけるようになっています。センター試験出題者は、こういう出題を工夫して欲しいと思います。最初でケアレス・ミスをやって最後まで気づかず、大問1題全滅、ということは、受験生には酷です。最後に四面体の体積が出てきますが、「外積」などと言う余計な技巧を使う必要もなく、なかなか良い問題だと思います。数学IIBの方は、満点の人も少なからずいると思いますが、当てずっぽうで正解できる問題もなく、分量が多いので、平均点はなかり低いように思います。毎年思うことですが、計算よりも、もう少し、概念理解とか解法を考えさせるような問題にするべきなのではないでしょうか?明日以降、大学入試問題研究サイトにおいて、各問題を検討してみたいと思います。追記1月22日、数学IAと数学IIBの第1問~第4問をアップしました。上記にリンクを貼ってあります。
2008.01.20
コメント(0)
-
電磁気の抵抗器の記号
予定通りに進行していませんが、大学入試問題研究サイトにおいて、電磁気の基礎事項を引き続き作成しています。抵抗器の回路記号が最近の物理の教科書では、ギザギザ記号から長方形に変更になっています。数学の教科書の「上端」、「下端」(私は、極限なので、「上限」、「下限」と言うべきだと思うのですが)の時にも、どうしようかと思いました。実社会でどちらを使うべきかという観点で、ギザギザ記号にするべきと思ったのですが、日本工業規格でも、長方形にしているようなので、基礎事項の中にある分を順次修正していきます。パソコン上で図を作成する上でも、ギザギザ記号は非常に面倒なので、原則として茶色(複雑な回路では黒にします)の長方形で書くことにします。センター試験がいよいよ間近です。センター試験に挑戦なさる方は、ぜひ、頑張ってください。大学入試問題研究サイト
2008.01.16
コメント(0)
-
あけましておめでとうございます
あけまして、おめでとうございます。本年もよろしくお願いいたします。大学入試問題研究サイトでは、物理の基礎事項を電磁気分野より制作を始めました。始めて思ったのですが、実は、電磁気分野の目次でリンクしているのはブログの各ページではなく、ホームページの方のページなので、ブログに入力しても、どんどん流れてしまうだけなので、あまり意味がないなと感じています。随分と方式も考えたつもりだったのですが、やってみると、不可思議なことが置きます。現状だと、修正はホームページの方のページに加えていくので、ブログで過去の日付からアクセスしたときに、修正が反省されていないということが起きてしまいます。目次からリンクされているわけではないので、大きな支障は出ないと思いますが、かと言ってブログの方のページにリンクするのでは、入試問題の検討をするときに、リンクを貼るのが非常に面倒です。この件については、もう少し、考えさせてください。それと、大学入試問題研究サイトのCSS(表示の方法を制御しているもの)に問題があって、10ページを超えるようなカテゴリーにアクセスできないことが判明しました。現在、直し方を考えているので、こちらについては、しばらくお待ちください。大学入試問題研究サイト
2008.01.02
コメント(0)
-
やっと、再開できました
やっと、再開できました。昨日のうちにデータ作成は完了していましたが、ただ、ブログにアップするだけで、朝から作業を始めて、今15時30分までかかってしまうのです。カテゴリーを作成し、各ページを表示させてURLを取得し、目次にリンクを貼りつける細かい作業ですが、カテゴリーを作っただけではカテゴリーのページが表示されず、一旦、カテゴリーの指定を解除して、カテゴリーを削除、新たに、カテゴリーを作成して、そこにカテゴリーを指定し直して、やっとリンク先を確定、と、まあ、面倒なことをやるしかないのでしょう。ご覧の皆さまには、簡単にやっているように見えるかも知れませんが、作成者は大変な思いをしてやっていることをご理解頂ければ幸いです。入試問題、基礎事項などのデータは、下記のブログで行い、こちらの楽天ブログでは、入試問題の検討、勉強法などについて書いていきます。大学入試問題研究サイト
2007.12.29
コメント(0)
-
再開します
長らく、停止しておりましたが、物理の基礎事項のページをどう構築していくか、という方針がまとまりまして、再開したいと思います。電磁気分野については、教科書の流れがコロコロ変わるので、教科書の流れを無視してやっていきます。「ゆとり教育」見直しで、来年以降、再び、教科書が大きく変わっていくことが予想されますので、ご了解ください。数学の授業で、数学はきちんと証明を積み重ねてできている、と、吹き込まれるので、物理についても、どうして、f=maとなるのか、とか、電磁気学の公式はどこから出てくるのか、証明して見せて欲しい、と、思う高校生がいます。私も、高校時代、そうでした。単に公式を並べて当てはめるだけの科目で味気なく、高校では一番嫌いな科目が物理でした。f=maは、神様が宇宙をそう作ったからだ、としか言いようがありませんが、電磁気学の理論的背景については、高校数学の範囲では扱えないので、普通の高校の物理の先生は、単に公式を暗記しろ、と、言うと思います。それも悔しいので、ベクトル解析まで踏み込んでウェブサイトを作っていくことにしました。ですが、高校物理では、電磁気学を理論的に実証していくことを要求していません。電磁気学の成果を利用できれば良い、という立場です。大学入試もそれで充分です。基礎事項理解については、カリキュラムがうまくできているとは言い難いですが、まずは、教科書の内容を理解することに努めるべきです。明日より、日々、下記リンク先において更新していきます。大学入試問題研究サイト
2007.12.28
コメント(0)
-
東工大物理2007年度前期の問題の検討
2007年度東工大前期の物理の問題を考察してみます。ことしの東工大の物理は厳しい内容でした。こういう時は、あまり無理をせず、無難な問題を確実に取っていく方が合格に近いように思います。力のある受験生が無理に難問にハマりこんで大ケガをしたのではないかと危惧します。第1問の、ベルトコンベア上の物体がバネにつながれている問題は、今年東大[1]でも出題されており、時々見かけるテーマで、いろいろと注意が必要です。東大[1]のように力学的エネルギー保存を用いて単振動の振幅を考えることが多いのですが、この問題では、「箱が滑っている時間が短く、その間のベルトの動きを無視する」という条件設定がついていて、この条件をどう利用するかということが問われる問題になっています。[B](e)で、箱が滑り出すときの各要素の間の関係を、この条件設定のもとでうまく処理するのは、限られた時間の中では困難だろうと思います。結局、摩擦の問題で、滑り出さない条件を考えれば済むことなので、[A](c)で用いたグラフを使って考えれば、滑り出した位置が振動端であることに気づけないことはないと思いますが、厳しかったことでしょう。無理をせず、[A]を無難に正答しておくことが合格する上で有利になったのではないかと思われます。第2問が、今年の3題の中では取り組みやすい問題で、これを落としてしまうと合格は難しかったと思います。気体の問題では、仕事のした、された、仕事の符号に充分に注意する必要があります。[B]では、入り組んだ状況のように見えますが、物理的状況をよく整理して、[A]の結果を利用せよ、というヒントをどう読むか、というところに神経を使ってもらえれば、完答できるでしょう。第3問は、波の絵を描いて、波がいくつ入るか、と、考えてゆけば大したことはないのですが、波の公式や正弦波の式にあてはめようとすると、問題文の意味がつかめないと思います。「物理」という科目は、「物」で理解する科目です。「文理」ではないので、絵を描いて実際の波の動きはどうなっているのかを「物」を見ているかのように把握しながら解答したいものです。とは言え、(d)では、問題文に記されている状況をよく理解して考えないと、時間ばかりロスすることになります。物理の試験と言っても、この辺は国語の読解力が問われるので、高校の授業で、「国語」の時間は理系の内職の時間というような学習態度では、東工大は無理です。将来、研究者として論文を書くようになれば論述力も必要です。この問題を見ていると、たとえ入試に必要のない科目でも、高校の授業を大切にして頂きたいと思います。(d)の意味がわかってしまえば、「精度」を問題にしていますが、後半は簡単な整数の問題でしかありません。どんな本にも書いてあることですが、難関大学の物理の問題をこなすためには、付け刃(やいば)的な学習は不可です。物理では公式の数は少ししかないので暗記して当然、公式の背景に潜んでいる物理的な意味をしっかり理解しておく必要があります。特にことしの東工大では、それが厳しく問われた、ということです。第1問[B]はやや、入学試験としては不適切に難しいように思いますが、確実に合格ラインに届く点数を確保した上で、残された試験時間を楽しませてもらおう、という感覚で取り組めば、点数につながる答案が書けるだろうと思います。CFV21大学入試問題サイトへ
2007.08.30
コメント(2)
-
東工大数学2007年度前期の問題の検討
2007年度東工大前期の数学の問題を考察してみます。ことしの東工大の問題は例年と比べるとやや取り組み易い問題だったように感じます。試行錯誤をいろいろとしてみないと解けないというタイプの問題はなく、どの問題もラクではありませんが、ていねいに見てゆけば最終解答にたどり着けそうです。第1問の整数の問題は、'91年前期[1]と同一テーマなのですが、'91年の問題の方が遙かに迫力がありました。'91年は、団塊ジュニアの時代で受験競争も熾烈を極めた時代、東大、東工大、京大が毎年、うなりをあげるような難問を出題していた頃です。3の5乗を3の3乗で割るとどうなるか、ということを調べれば、問題の仕組みはすぐに分かります。場合分けも単純で、第1問としては、適切な出題だと思います。(2)が問題文を読むだけでは戸惑うかも知れませんが、(1)がついているので、落とすわけにはいかないだろうと思います。第2問は、数学IIの微積と極限を組み合わせた問題で、それなりの計算をさせながら、b/aの極限がうまい数になるように仕組まれていて、出題者のセンスを感じさせてくれます。類題をいろいろと作れるので、今後、予備校の模試や地方国公立の入試問題で、この問題の変形パターンが流行するだろうと思います。やることは、2直線のなす角が指定されたときに正接の加法定理を使う技巧と、定積分の公式の利用だけなので、入試会場では、第1問と同様に正解しておきたい問題です。第3問は、答はすぐに分かりますが、論証が大変な問題で、ことしの4題の中では、最難関の問題だったと思います。恐らく、採点も大変で、100人単位の教授が、3日3晩不眠不休で採点しなければならなかっただろうと想像します。それだけ、日本の科学技術を背負って立つ技術者を育てるために、受験生の探求心を試そうという意欲的な出題と言うことができます。答案を書くポイントは、論証の抜けがないように注意する、ということです。東工大の前期の数学は、充分に時間が与えられているので、焦ることなく、丁寧に場合分けを考えていくことが大切です。大学入試問題サイトに示した解答は、入試会場向けに最も素朴な方針で考えたものですが、「大学への数学」4月号や、旺文社の「全国大学入試問題正解・数学」には、より優れた考え方が紹介されているので、参考にしてください。第4問は、計算が面倒な上に、解答が汚い形になりますが、東工大の計算問題ではこの問題よりも遙かに面倒なものも出題されたことがあります。この程度で投げ出すようでは、一流の研究者・技術者になることはできません。最後の部分が、やや出っ張った感じなのですが、これを気軽に抜かして考えてはいけません。東工大では、はさみうちの原理を使う極限の問題が頻出なので、はさみうちを使って、きちんとした答案を書くようにしてください。ことしの東工大数学は、第1問で勢いをつけて、第2問のきれいな答を見て加速し、第3問で、ちょっと考え込み、一応のところまで攻めておいて、第4問で計算ミス・勘違い・早とちりに注意する、という、起承転結型の戦略で臨めばよい、という感じでしょうか。CFV21大学入試問題サイトへ
2007.08.04
コメント(0)
-
東大物理2007年度前期の問題の検討
定常的に更新して行きたいとは思っているのですが、またまた、休眠状態が続いてしまいました。2007年度東大前期の物理の問題を考察してみます。このところ、東大物理は比較的穏やかな問題だったのですが、今年は考え込んでしまう部分があります。何も考えないで多分こうだろうと安易に考えてしまう方が正解できてしまうかも知れませんが。東大内部で、物理は少し易し過ぎるのではないか、という意見が出ていたのかも知れません。第1問の力学の問題は、バイオリンの弦を題材にしたような問題文になっていますが、ベルトコンベアの問題で、以前にも難問が出題されたことがあるテーマの問題です。前半部分は、基礎的な問題ですが、基礎事項に忠実に考えてもらわないと正解できません。物理では勘に頼ると必ず出題者に裏をかかれるので、教科書に書かれている内容に即してていねいに考察することが大切です。後半部分は、力学的エネルギー保存則を考えます。単振動の途中で速度と変位がわかっていて振幅を求める問題では、エネルギー保存の式を立てるだけで容易に解答が得られます。この考え方は、必ずマスターしておくべきです。最後のII(4)が難しいのですが、要するに、ベルトコンベアに強い力で押さえつけてしまうと、それだけ余計の距離、ベルトコンベアにくっついて動き、周期も長くなる、ということです。振幅が大きくなっても、単振動の周期には変化がないことに注意してください。第2問の電磁気の問題は、円筒形の導体の中で円形の磁石を落下させると、レンツの法則による反発力を受けて、一定速度で落下するようになる、という問題です。この手の問題では、普通は、運動方程式を立てさせて、速度が一定になる状況を考察させることが多いのですが、この問題では、問題文中にその状況が書かれていて、解答に対する要求からは省かれています。数学の得意な方は、微分方程式を立てて解けば、速度一定になる状況がわかると思います。ただし、試験場で「どうして速度一定になるのだろうか」という方向に脱線すると第1問、第3問を考える時間がなくなるので注意してください。この問題は、しっかりと基礎学力をつけた受験生であれば、問題文の指示通りに解答すれば正解できるので、落とせない問題です。第3問の波の干渉の問題が手こずるかも知れません。余計な心配をしないで安易に考えてしまう方が正解できるかも知れません。IIは、一見、単スリットの問題のように見えるのですが、単スリットで考えると正解できません。II(3)は、すき間の幅が広がると通過する波が多くなる、というところにポイントがあります。出題者は、考え方の道筋を指示するために、「x=0から出た円形波の変位が点Pでゼロである瞬間に、すき間内の各点からくる円形波のすべての変位が点Pで同符号である(強め合う)」という書き方をしてくれているのですが、この記述をヒントと見ないで、正攻法で考えようとすると、試験場の限られた時間の中では混乱してしまうかも知れません。複雑になりそうなときには、問題文の指示するところの意味をよく把握するように努力して頂きたいと思います。物理の場合、問題をざっと眺めただけでは、難易度の判断ができないのですが、今年の東大物理では、1題ずつ、時間を20分で制限しながら見ていくという進め方しかないだろうと思います。CFV21大学入試問題サイトへ
2007.07.26
コメント(0)
-
今年の東大物理前期第2問をアップしました
長らく、止まってしまっていましたが、ことしの東大物理の前期第2問をアップしました。URLは、以下です。http://www.cfv21.com/
2007.07.06
コメント(0)
-
東大数学2007年度前期の問題の検討
再び長らくお休みしてしまいましたが、復活します。きょうは、2007年度東大理系前期の数学の問題を考察してみたいと思います。難易度は例年と変化なしという評価が多いようですが、私は、やや易しく、分量的にも小ぶりだったように思います。ですが、普通の国公立大学のレベルと比較すれば、格段の差があるので、東大理系を目指す受験生は安易な気持ちを抱かないで頂きたいと思います。第1問の数学的帰納法の問題ですが、東工大でよく見かけるタイプの問題です。東大受験生なら、証明すべきことが何かということはすぐにつかめると思いますが、数学的帰納法の形にまとめるのが意外と大変な問題です。東大理系でも上位の1割くらいは、これくらいであれば、構想数分でスラスラと答案を書き上げてしまうのですが、一般的レベルの受験生は、即座に答案を書き始めないで、まず、数学的帰納法の証明のストーリーをじっくり練ることから始めてください。この問題では、数学的帰納法の構造を考えるところに注力してください。あやふや点をクリアにしてから、答案を書き始めるべきです。合格のためには、30分以上かけてでも完答すべき問題です。第2問は、普通の国公立大学の入試問題として標準レベルの問題です。余弦定理や極限に関する基本ができているかを見ている問題で、この問題は絶対に落としてはいけません。逆に言うと、このくらいの問題でも難しく感じる受験生は、まだ基礎力が弱いのです。難関大学の入試問題にアタックする前に、学校の数学の授業で使うような基礎的な問題集を1ヶ月くらいの間に仕上げてください。この問題の答案が15分くらいで書けるレベルを目標にして、1日2時間以上、しかもその間、完全に数学に没頭するという感覚で、集中力を身につけながら、スピードもつけながら、みっちり練習を積んでください。第3問は、単純な2次関数の問題に見えますが、構造的にも複雑で難問です。解答を書く作業も手間がかかる問題です。要領の良い受験生なら、論理展開の不備による減点を多少覚悟してでも、計算用紙で計算しつつ、要点だけを拾い出して、グラフや図を多用しながら、解答を書くと思いますが、この問題を懇切丁寧に完璧に説明し尽くそうと思ってしまうと、他の問題に回す時間がなくなります。本年度の問題でも、6割程度を取れば充分合格ラインに入ります。無理をせず、各問題のバランスを考えながら、答案を書くように心がけてください。なお、大学入試問題研究サイトでは、考え易いように「2次方程式の解の配置」という技巧を用いて解いてありますが、この技巧が使える問題は、2次関数の最大最小の問題として解くこともできます(簡潔になりますが考えにくくなります)。第4問は、受験技巧がものを言う問題です。東大でも毎年必ず、よく勉強してきた受験秀才の努力に報いてあげよう、という問題を出します。その中では、「スペクトル分解」はマスターしている受験生の少ないテーマですが、最近、早稲田理工でも出題されています。他大学の過去問で採り上げられているテーマについても関心を持っていて欲しいという出題意図だと思います。東大理系を狙うのであれば、一通りの受験技巧はすべてマスターしておくべきだ、ということです。第5問の確率の問題は、難易度としては大したことはないのですが、場合分けを見落とすと命取りとなります。こういう問題は、科学技術に対する慎重さ、注意深さを見ようとしているのか、わかりませんが、細心の注意を払う必要があって、意外と正解しづらい問題です。こういう問題に対処する注意力を養うためには、数学をしっかり勉強するというよりも、友達づきあいにおいて、友人が一つの言葉でどのように感じるかを友人の目の表情から読み取るようなことを普段から心がけたり、ボランティアに出かけた福祉施設で、障害者の方にどのようにケアをしたら良いかを考えたりすると良いのです。あるいは、いろいろな模擬試験をたくさん受けて、たくさんケアレス・ミスをやって、どうしてミスしてしまうのか、自分の精神構造にまでさかのぼって、自分を見つめ直す、ということも良いと思います。第6問ですが、(1)の図形的考察は、東大受験生なら誰でも気づけると思います。説明が面倒なので、この問題は、引いて微分して計算で対処する、と言う方が、答案が書き易いかも知れません。問題は、(2)です。本年度の問題では、この問題が最後に来ているので、大ケガをする受験生はいなかったと思いますが、こういう問題が第1問に来ていることもあるので、ハマらないように充分に注意してください。一度手がけると、その問題が解けるまでその問題のことが頭を離れなくなる、というタイプの受験生は、この問題で、(a+x)/(a-x)=2として、うまく行かなかった時点で、一旦、断念して他の問題に移り、この問題のことを忘れて次の問題に集中する、という精神的なトレーニングを必ずやってください。ダメな問題にこだわってしまうと、合格切符は逃げてしまいます。実際の入試では、恐らく、数学を得意とする受験生で、完答している人が数十人はいると思いますが、本年度の易しめの問題でも、私は、合否の分かれ目は5割を切っていると思います。実は易しい問題が難問に見えてしまったり、単純ケアレス・ミスに気付かずにその先で解答不能に陥ったり、問題文の条件を見落としたり、で、なかなか、思うように解けないのが普通です。試験会場で、異常心理状態になってしまったり、急激に腹痛を起こしたり、ということもあります。本年度の問題でも、私は無理に満点を狙わずに、安全を考えて取り組むべきだと思います。まずは、第1問、第2問を完答することが第一目標です。英語や理科が得意という受験生は、これだけでも合格できます。第4問がスラスラ書けるのなら、第5問で場合分けを忘れてしまっても、大きな被害にはならないでしょう。ですが、第4問で手間取るのなら、第5問も落とすことはできません。第3問、第6問は、残された時間の中でできる限り取り組んでおけば良いと思います。試験開始となり、一通り、第1問から第6問まで見渡して方針を立てるときに、第5問の確率が簡単そうだ、ということに、気づけると思います。ですが、試験会場で易しく感じる問題にこそ充分に注意が必要です。第5問のような問題でのミスは気づきにくいので、本年度の問題の中では、この問題を最初に解答して、第1問、第2問、スペクトル分解を知っていれば第4問、第6問(1)と解答したところで、一度、この確率の問題に戻り、新鮮な気持ちで問題・解答を見直すと、場合分けの抜けているところに気付き易くなります。その後、第3問、第6問をできる限り考察し、他の問題の解答を一通り見直してから、最後の5分くらいで、再度チェックする、くらいで万全でしょうか。CFV21大学入試問題サイトへ
2007.04.04
コメント(0)
-
システム切替中です
11月26日の日記でもご案内いたしましたが、大学入試問題研究サイトにて、データ作成の入力システムを新システムに切替中です。ライブドア・ブログでの大学入試問題研究サイト上で、特殊文字を表示した場合に表示が崩れてしまいますが、これは、当方の新システム上の問題点です。調査を継続し、できるだけ早く修正するように努力中です。--------------------追記修正できました。きちんと表示していると思います。
2006.11.30
コメント(0)
-
一週間、更新が滞り、申し訳ありません
一週間、本サイトも大学入試問題研究サイトも、更新が滞ってしまいました。現在、制作システムを新システムに入れ替える作業をしております。年内のうちに、ということで、ゆっくり作業する予定でいましたが、諸般の事情により、急がざるを得ないことになり、11月中に本格作動させるべく、努力中です。この土日で、だましだまし何とか動作するようになってきましたので、次に更新されるものから、新システムにて制作作業を行うつもりです。旧システムでは、能力をほぼ限界まで使っており、これ以上の機能拡張が不可能でしたが、新システムでは、機能拡張が柔軟に行えるようになっています。現段階での機能拡張は、文字に色をつけられるようにした点、インデントをつけられるようにした点、京大の物理、慶応理工の数学の問題に出てくるワク囲いに対応した点、その他、新企画のために、省力化するための改良を行いました。日本の科学技術の発展のために、日々努力されている皆さま、まだまだ、頑張る所存ですので、よろしくお願いいたします。CFV21大学入試問題サイトへ
2006.11.26
コメント(0)
-
東大受験生に、国語の勉強法について
本日は、東大理系受験生向けに、国語について考えてみましょう。東大以外では、関係ないかも知れません。私は大学は理学部物理学科出身ですが、中学3年の頃から高校1年頃にかけて小説家を志していて、小説や難解な評論を片っ端から読みふけっておりました。小説もどきを書きためながら、学校の勉強はそっちのけ、成績は下がる一方でした。その頃、ノートになきなぐったものも、どこかに雲散霧消してしまって、無駄な時間をずいぶん使ったもんだと思います。学校の古典漢文の授業は昼休み後の5時間目にあって、常に昼寝の時間でした。古典漢文も当然、サッパリです。高校1年の3学期に、学校の数学では「複素数」というのをやっていましたが、完全にちんぷんかんぷんで、中間試験は何もわからない、という状況にまで至りました。当時、「生物」という科目が、ある事情があって非常に嫌いで、「生物」が1学期、2学期、赤点でありました。私の学校では、2科目赤点をとると落第させられてしまうので、やむなく、数学の勉強を始めて、何とか高2に進級しました。確か、中間試験が実質零点で、期末試験が90点くらいだったと思います。数学の先生に、君はずいぶん波が激しいね、などと言われた覚えがあります。高2になるときに、Z会の通信添削を始めました。Z会も、受験科と基礎科しかなかった当時と、様変わりしてしまってちょっと寂しい気がしますね。大学ごとにコース分けしないと、受験生が集まらないのでしょうか?Z会、英語と数学は、高2の夏休みに猛特訓するまで全くできませんでした。ですが、国語は、それまで勉強したこともなかったのですが、現代文の方は何とか闘えるんだ、ということに気付いたのです。ただ問題文を読んで、聞かれている問いに素直に答を書いているだけなのに、平均点を遙かに上回る点数が取れるので、自分でも不思議に思っていました。今はどうやっているのか知りませんが、当時のZ会の国語は、問題用紙が巻物のように細長くて、現代文の問題文は、読むだけでも30分から1時間くらいかかるような長文でした。小林秀雄という評論家の書いた文章が採り上げられた問題の講評に書いてあったと思うのですが、娘さんが、「この文章、何を言っているか全然わからない」と言って持ってきた文章を見て、小林秀雄さん、「これは、とんでもない悪文だ、こんな文章はわからなくていい」と言ったのだそうです。ところが、娘さんが言うのには、「これ、お父さんの文章だよ。」こういう著述家の文章ばかりが問題に採り上げられるので、Z会の答案を作るのも大変でした。古典漢文は、全くわからないので、すべての単語を古語辞典で調べる、ということをやっていました。というわけで、国語の一回分を仕上げるのに、数十時間を費やしていたと思います。高3の一年36回分のうち、数学は全部答案を書いてZ会に送りましたが、国語の答案を出したのは10回くらいですね。でも、制限時間の10倍も時間をかけてやるので、出したときはほとんど40分の1の成績優秀者に入っていて、しかもそのうち2回は、東大文系志望の諸氏を差し置いて第1位の栄誉に輝く、ということで、国語には自信を深めておりました。一度、苦境に立たされ絶望的な状況を書いた文章が出題されたときに、この文章の作者の叫びを漢字一文字で表せ、という問題があって、私は、苦悩の中で生への指向を強く訴えている文章だと思って、素直に「生」と書いて答案を送ったのですが、まわりの友人が、自殺一歩手前の文章で「生きる」わけないだろ、「死」に決まっているじゃないか、みたいに、コケにされたことがありましたが、正解は「生」でした。それと、Z会の冊子に投稿欄があり、当時、赤軍派の浅間山荘事件など、物騒な事件が頻繁に起こっていた頃で、こうした暴力集団は許せん、という、右翼的文章を載っけてもらっていました。しかし、これが、左翼系に激しく批判されて、激しい罵声の応酬になったことがありました。世の中にはバカなヤツがいるもんだと思っていましたが、不愉快なことに、私とやり合っていた連中も皆、東大に入ってきました。ですが、東大で学費値上げ反対運動や自主ゼミ推進の活動したのは私の方で、やりあっていた連中は何か運動でもしていたのでしょうかね?結局、国語は、Z会の答案を10回くらい送った以外は何もしませんでしたが、入試では、古典漢文は恐ろしく易しく、現代文も含めて、自分では完璧に書けたと思っています。予備校の現代文の授業で、いろいろな記号をつけて読解していくテクニックなどをやっているように聞きますが、小説やオピニオン誌を読むときに、あんな風に、記号を入れて読んでいる人なんているんでしょうかね?国語を技巧的に扱って点数を取ろうというのが私は間違いだと思いますね。そんなことよりも、自分で評論とか小説とか書いてみればよいと思います。できれば、対立する人と激しくやり合うと良いと思うのです。世の中には種々雑多な価値観を持った人がいます。そういう人たちに自分の主張を納得させるのには、どういう書き方をすればよいのかを必死に考えているうちに、「傍線部分と同じこと意味する部分を前段から抜き出せ」とか、「○○という言葉で作者が言おうとしていることをわかりやすく説明せよ」という問題に自然に答えられるようになるのです。自分で文章を書いていると、説得力を強化するために、同じ内容を異なる観点からくり返し主張したくなります。過去の失敗に学ぶべきだということを言わんとして「理系でも歴史を勉強すべきだ」と主張するときに、「第二次大戦に学んだからこそ、憲法9条を貫く日本の経済的繁栄がある」と、言うこともできるし、「いろいろな実験の失敗の教訓の中から新しい理論のアイデアが湧いてくる」と、言うこともできます。このときに、入試問題は、傍線部分を同じ意味の部分を前段から抜き出せ、と、言ってくるのです。また、文章を書いていると、長々と説明したことを別の部分で、また使いたくなることがあります。そういうときに、同じことをまた長々と説明するのは面倒なので、簡単に一言で言い表してしまおう、ということをやりたくなります。このときに、入試問題は、その一言を、わかりやすく説明せよ、と、言ってくるのです。書き手の立場で考えれば極めて自然なことをそのまま答案に書けば点数が取れる、というのが国語です。国語のテクニックをマスターしよう、などというヒマがあるのなら、新聞記事や新聞社説に対して意見を書いて、友人同士で読み合ったり、親や学校の先生に読んでもらって批判してもらう方が遙かに得点につながると私は思います。本来、国語というのは、自分の主張を相手にわからせるための道具です。そういう視点に立って、本来の勉強法を心がけて頂きたいと思います。CFV21大学入試問題サイトへ
2006.11.20
コメント(2)
-
悩みを抱えながら頑張っている受験生・高校生の方へ
昨晩の8時30分頃、横浜市戸塚区品濃町のマンションの10階から私立高校2年生の女子が飛び降りてしまったそうです。私が、電車に乗って東戸塚の駅を通り過ぎたのが7時30分頃なので、私が電車の窓から眺めていたマンション群のどこかに、悩んでいる女子高生がいたのかも知れません。東戸塚のオリンピックにもよく買い物に出かけるので、すれ違ったことがあるかも知れません。私は、大船にあるカトリック系の高校を出ましたが、この高校では、自殺は大罪であり地獄に落ちるぞ、と教えていました。高3のときに私の左の隣の隣に坐っていた友人が、私の学年では唯一東工大に現役合格した友人ですが、大学2年のときに、横浜駅で電車に飛び込んでしまいました。あとで、大学の合唱部で一緒だったという人から、指揮者になれなかったことを苦にしていた、と、聞きました。「いじめ」問題が出てきてから、中学生・高校生の自殺のニュースが相次いでいます。自殺した人に激しい非難の言葉を浴びせる人もいますが、苦しみに耐えかねて、あるいは、希望の灯が消えてしまって、命を絶つという選択をしたことを、私には非難することはできません。どうか、来世においては、この上のない幸福をつかんで欲しいと思います。ですが、このブログでも、そして、大学入試問題研究ブログでも、私の会社のホームページでも、メールやコメント欄を受け付け可能にしてあります。私のブログに気付かなかったのかも知れませんが、広報の努力も一応やっています。どうして相談のメールを送ってくれなかったのでしょうか?私自身、これ以上生きていても無意味だと思うような、耐えきれない苦しみを抱えながらも、大学入試問題研究ブログを作っています。別にやっている個人ブログの方には、私の個人的な事情も荒れた文章ですが書いてあります。東大の問題の解答をカッコよく書いているように見えるかも知れませんが、入試問題の解答をアップしているときに、苦しくて、悲しくて、涙を流しながらアップしている時もあるのです。これをご覧の受験生、高校生の皆さんの中に、苦しい気持ちを抱えている方がいらっしゃるのなら、どうか、私にメールをしてきてください。このブログのメールの入り口のリンクはHOME画面の左袖の上の方にあります。メールを頂いたから何かしてあげられる、ということではありませんけれども、他の誰かに苦しみを打ち明けているだけでも気持ちが和らぐ、ということがあるのです。そのときに耐えきれないような激しい痛みであっても、あとで思い返してみれば、良い想い出になっている、ということがあるのです。余りに早すぎる決断をしてしまわないように、お願いしたいと思います。CFV21大学入試問題サイトへ
2006.11.18
コメント(0)
-

東大理系数学'05年前期の問題について
大学入試問題サイトで、東大理系の昨年度の更新をしておきました。私の受ける印象を書いておきます。旺文社・大学入試問題正解の2006年受験用版の東大前期の講評を見ると、合格者を選別する、という目的においては、少々問題が難しすぎるのではないか、と、書かれています。書いているのは、受験界において著名な人です。実際、難しい問題は受験生には可哀想だ、教科書程度の基礎学力を観るので充分なのではないか、そういう声もよく聞きます。ですが、私はこういう考え方には反対します。こうした考え方では、日本の科学技術の将来はお先真っ暗になります。何としても、意欲溢れる受験生には、東大の難問にチャレンジして頂きたいと、私は思います。科学技術の最先端のところで頑張るときに、必ず、超えがたい壁にぶち当たるときがあります。高い電圧をかけなければ期待する反応が起こらないのに、高電圧をかけても耐えられるような素材が見つからない、というような、相矛盾した要求を満たすような解決法を探す場面に出くわすのです。そうしたときに、教科書に載っていないから解決できませんでは、負けです。ここでこそ、東大入試の難問にも取り組んだ、というチャレンジ精神が功を奏するのです。東大でも、2002年度の入試は易しく、高得点続出なのではないか、という年がありました。しかし、こういう年は、英語や国語で合否が決まってしまい、数学を得意とする受験生は涙を飲むことになっただろうと想像します。この年の、旺文社・入試問題正解の東大前期の講評のところにも、易しすぎるのではないか、と、書かれているのですが、1973年の入試でも前年が難しすぎたために異常に易しくなった年がある、という記述が見えます。実は、1973年の前年、1972年の入試を私は受けています。数学に絶対の自信をもって試験に臨んだ私でしたが、数学が2問しか完答できず、数学の試験終了後は、もうだめだ、と、思いました。後からよく考えると、残り4題も決してできない問題ではなかったのですが、最初に取りかかった空間図形の問題が解けないショックが大きく、動揺が抑えられないまま、試験時間が終わってしまいました。ところが、入学してみて驚いたのですが、周囲に聞くと、数学は1題もできなかったのに合格してしまった、という人ばかりだったのです。いろいろなゼミにも出て思いましたが、数学に自信を持っていた私の遙か上を行く実力者が何人もいました。私が持っている数研出版の教科書の執筆者にも名を連ねていますが、現東大教授の坪井俊さん、法政大教授の雪田修一さんなどもそうです。私は、どちらかと言えば、国語で合格できたようなもので理系の合格者と言えるのか、と思いますが、もし、数学の試験が易しかったら、数学のエキスパートとも言えるような人たちが東大入試をクリアできたのでしょうか?数学の試験が難しければ、数学の得意な受験生が数学で高得点を取り、数学を苦手とする受験生は低い得点となり、ここで差がつきます。しかし、数学の試験が2002年度のように易しいと、数学が苦手と言っても東大受験生はそこそこの問題はできます。数学で点数の差がつかなくなるのです。結果的に、英語や国語の点数で合否が分かれ、数学のエキスパートは合格できない、という、理系の試験にあるまじき結果となります。2006年度の入試では、完答は、数学は確率の問題だけ、ほかは全部途中まで、という合格者もかなりいると思います。それでも、数学を得意とする受験生が合格してくれれば良いのです。合格者の平均点がどうかという問題ではなく、数学の実力の順に数学の得点が並んでくれるか、という問題です。昨年度の問題を見てみます。第1問は、商の微分法の計算をして、導関数の中に出てくる数列の規則性を見破ればよいので、落ち着いて見ていけば誰でもできる問題です。完答できるかどうかの分かれ目は、規則性が見破れるかどうかの一点です。試験場の雰囲気ではどうか、ということはあると思いますが、私としては、東大受験生でなくてもできて欲しい問題です。第2問は難問です。私なら、やれる限りのことをやって、あとは放棄します。150分の試験で、他の問題もそこそこ書いてなお、この問題が完答できるなら、その時点で合格を確信して良いと思います。手を抜くとすれば、θが180度のときに最大になる、と、書いて、cosθ=-1として、|w|の最大値を考えてしまえば良いでしょう。この難度では、これで減点されても、半分くらいの点数は確保できると思います。数学的に厳密にやろうとすると、他の問題を解答する時間がなくなります。ちなみに、この問題の旺文社入試問題正解の解答は白眉です。これが思いつければ、この問題はものにできます。第3問は、定型パターンの問題で、この問題は、平均値の定理を使えばよいことを知っているかどうかで決まります。こういう受験テクニック的な問題も、東大は毎年必ず混ぜています。受験秀才にも道を開いてあげよう、ということでしょうか?第4問は整数の問題ですが、東大や東工大の整数の問題としては易しい部類です。雑誌「大学への数学」でもよく強調されていますが、実験せよ、手を動かせ、ということで、a(a-1)と因数分解して、aか(a-1)のどちらかが、偶数で、どちらかが奇数、ということに気付けば、それで解決に至るでしょう。この問題も、東大受験生でなくてもできて欲しい問題です。第5問は確率の問題ですが、あまりに易しい2007年度の確率の問題は別として、東大の確率の問題は、あまり真剣にやらない方がよいように思います。場合分けが複雑で、場合を見落とす可能性の高い問題が多く、それほど難度の高い問題でなくても、正解するのが難しい問題が多いのです。この問題もそうした問題です。最後に、余力があれば、しっかり見直す、ということで対処すべき問題だと思います。第6問は、定石通りに、立体を断面で切って、断面形状を素直に考えていけば良いのですが、立体の形状にこだわると破滅します。計算はやや面倒なので、体積を求める定積分の式だけでもしっかり書いておくことが大切です。こういう問題は、最後に時間的余裕があれば検算するとしても、完全解答を狙うべきではありません。なお、入試会場での要領の良い解答の書き方は、下記の本を参考にしてください。 CFV21大学入試問題サイトへ
2006.11.17
コメント(0)
-
この時期だから、の、2次試験「物理」対策
理系受験生向けに、11月中旬時点での2次試験の「物理」の対策について書いておきます。まず、いろいろな本に書いてあることですが、物理は「物」を「理解」する科目です。参考書の文章や解法パターンを字面だけ暗記して回るような勉強法は全く意味がありません。実際に起こる物理現象が今、目の前で起こっているかのように思いながら、基礎事項からていねいに考えていく勉強法を心がけてください。物理のセンター試験対策のところにも書いておきましたが、私は、「物理」は基本的に、センター試験用の勉強と2次試験用の勉強を分けない方が良いと思っています。物理Iと物理IIの範囲の分け方は、受験生のセンター試験の負担を軽くするためにかなり無理をしていて、理系の受験生にとって非常に不幸な状況にあります。個人的には、センター試験の数学や理科は(地歴公民もかも知れませんが)、文系用と理系用をはっきり分けてしまって、理系用には、高校物理の全範囲を試験範囲とする方が、理系受験生にとってやりやすいと思っています。従って、センター試験までは、センター試験用に、物理のセンター試験の範囲だけを勉強するというような方針は立てない方が利口だと申し上げておきましょう。センター試験の注意のところでも書きましたが、物理のセンター試験の範囲は、高校物理全範囲の部分集合になっていて、しかも、選択肢問題である、とか、計算をあまりさせない、というようなことを除けば、センター固有の問題、というのは、あまり見られません。2次試験用の勉強で物理の全範囲に渡って総合的に理解を深めながら、その中でセンター試験の問題に対処する、ということで、充分に対応できます。高校で習っている物理の先生の方針、あるいは、塾・予備校の先生の方針によっても、変わってくるかも知れませんが、私は、力学分野・電磁気学分野については、センター試験用の問題集もやるとしても、志望校や志望校と同レベルの大学の過去問をていねいに解いていくことを中心にすべきだと思います。問題集であれば、数研出版の「重要問題集」あたりが最近の問題を主にしていて手頃だと思いますが、入試会場では、1題20分くらいのスピードでやって行かなくてはいけないとしても、入試の準備段階では、1題に数時間くらいかけて、教科書の該当箇所の説明を読んで復習し、基礎事項や物理法則を確認しながら、ていねいに進めていく、という勉強法をオススメします。たくさんの問題を雑駁に解いて解答が合っていることだけで満足し、物理の基礎事項を勘違いして理解してしまうことが本番での大きなミスの原因となってしまう、ということがよくあるのです。たくさんの問題に当たるよりも、深い内容の問題を選んで、1題の問題の中で、その分野で関連する事項をあれこれ考えておく、というのが理想的だと思います。波動分野については、すべて物理Iの範囲でセンター試験の範囲です。波動は、2次試験の出題頻度があまり高くないのにもかかわらず、内容が多岐にわたっており、かと言って、難関大学の入試問題を見ているとそれなりに高度な内容まで出題していて、非常に勉強のしづらい分野です。波動分野の頻度が最も高いのがセンター試験とも言えるので、幅広く基本的なことを勉強するという観点では、波動については、教科書を熟読した上で、センター試験の過去問10年分くらいの中から波動だけ拾って広く解いておく、ということをオススメします。難関大学の2次試験の波動の問題を、波動の全分野見ているのでは、やりきれなくなるか、他の科目の勉強にしわ寄せが行く恐れがあります。少なくともセンターまでは、難関大の過去問は、せいぜい頻出のドップラー効果にとどめておく方がよいのではないでしょうか。現行課程で理系受験生に気の毒なのが、物理IIで選択項目となっている、「物質と原子」、「原子と原子核」です。高校の先生が物理学科出身で素粒子の理論物理をやった人なら「原子と原子核」を選んでいるかも知れません。物理学科でも「材料関係」を専攻した人とか、工学部出身の先生だと「物質と原子」を選ぶだろうと思います。大学によっても、取り扱いにばらつきが見られるので、不運を嘆くよりも、どちらの項目もしっかり教科書を読んでおくと良いと思います。試験に出なかったから損をした、などと思わないで、それなりの素養を身につけて、入試問題を解くための遠いヒントにはなったかも知れない、くらいに考えて欲しいと思います。物理は、東大前期の問題よりも、東工大、京大の問題の方がやや難しい気がします。東大理系前期の場合、古典漢文まで試験をするので、物理が難問揃いでは、東大理系受験生の負担が重すぎるということだろうと思います。その分、東工大では状況設定の複雑な問題が多く、長い問題文の読解だけでも骨が折れます。東工大では、物理が現代文の問題を兼ねていると言っても過言ではありません。従って、読解力をつけるという観点からも、たとえ入試の範囲でなくても、「物質と原子」、「原子と原子核」の両方にわたって、教科書をしっかり読んでおくべきです。余力が有れば、物理問題文の読解力をつけるために、「ニュートン」という科学雑誌にも目を通しておくと、どの辺の分野が出そうか、など、ある程度予測が立ちます。物理の出題者も、ある程度は時事問題を意識していて、宇宙に関する話題の出た次の年には、万有引力の問題が多くなります。雑誌が採り上げるテーマは、時事的な話題から来ているので、入試問題のヤマをかけるのにもある程度は役に立ちます。物理の2次試験用に、コンパクトに整理された良い本がないのも困りものです。駿台の「物理入門」を薦める人もいますが、入試対策向きの本ではないし、私なら、大学教養課程の参考書、例えば、裳華房「物理学」(小出昭一郎著)を読む方が得るものは大きいと思いますね。昔は、前田和貞さんという人の書いた「受験の物理」という優れた本があったのですが、物理のカリキュラムが変わるうちに本屋さんで見なくなってしまいました。物理を選択する高校生が減っていて、物理の参考省が売れないので、良い本を作るだけの資力のある出版社がないのが残念です。物理を苦手にしている人にだったら、「橋元流」を薦めておきます。物理が得意な人は、物理の参考書を探すよりも、英語の勉強に時間をかける方が良いのでは?冒頭にも書きましたが、「物理」という科目は、すべてのパターンを暗記する、という勉強法を採ってはいけません。ドップラー効果だけでも、観測者が近づく場合、遠ざかる場合、音源が近づく場合、遠ざかる場合、風が吹く場合、吹かない場合、斜め方向でのドップラー効果、など、場合分けすれば多種多様になります。受験生全員が、この一つ一つの場合の解法を覚えきれるほど博覧強記の秀才というわけではないと思います。暗記すべきことは、ドップラー効果の公式の考え方一つだけです。ドップラー効果の公式一つなら、すぐに覚えられます。あとは、ケースバイケースで公式を変形させて、問題を解いていくのです。こういう公式、基礎事項は、「物理」では驚くほど少ないのです。「物理」を試験科目で選択する意味は、「化学」や「生物」の半分の時間で入試の準備ができるという点にあります。暗記に走って時間をかけるのなら、「物理」よりも「化学」、「生物」を選択する方が、勉強量に比例して得点を伸ばすことができます。できる限り短い時間で、より高得点をとる、ということを「物理」の勉強の目的にしてください。これを読んでくださった受験生の成功を祈ります。CFV21大学入試問題サイトへ
2006.11.16
コメント(0)
-

この時期だから、の、2次試験「数学」対策
11月中旬時点での理系受験生の「数学」2次試験対策を書いておきます。センター試験まであと2ヶ月の時点で、センターも迫ってきたからセンターの準備に全力投入、と思って失敗する受験生がいるからです。2ヶ月間センター試験にズッポリはまって、1月終わりから2次試験対策を再開する、というのは誤りです。2ヶ月も空けてしまうと、数学の感覚が完全に鈍ってしまいます。センター試験で高得点を取っても、2次試験で失敗しては何にもならないのです。センター試験の準備を必死にやって、進学した大学が慶大理工だった、ということがよくあります。慶大理工のA問題は空所補充式なので、センターと若干感覚が似ていますが、一般の国公立大学の数学の入試問題は論述式がほとんどです。センター試験のように答さえ合えば、という感覚では、2次試験に臨むことはできません。センター試験が近づくにつれて、2次試験準備とセンター試験準備の割合を次第に、センターに比重をかけるように高めていくようにする、という方針を立てるようにしてください。11月のうちはまだ2次試験が7で、センター試験が3の割合。12月中旬くらいで、5対5。正月明けくらいで2次試験が3で、センターが7。センター1週間前でも、2次試験が2で、センターが8くらいです。センター試験前日以外は2次試験用の勉強をゼロにするべきではありません。もっと言うと、センター試験会場で、時間の余裕があるなら、グラフを書く問題や、面積・体積の計算問題をやっているくらいで良いのです。(日本の科学技術レベルを維持したいのなら、センター試験の範囲に数学III・Cも含めるべきだと、個人的には思います)理系受験生にとっては悩みのタネの地歴公民ですが、11月のうちから、暗記作業をやり出すと、1月20日までに忘れてしまうので、何度も覚え直しをやらなければならず、時間の無駄になります。11月のうちは、教科書やセンター試験用にまとめられているものを何回か読み通し、問題集に多少当たっておく程度で良いのです。地歴公民が得意な人を除いて、12月に入ったら、センターで50点を取れるレベルに引き上げ、正月明けの頃から一気にという感じで80点を狙うくらいで妥協すべきです。理系受験生にとっては、地歴公民は日本人としての常識レベルのことをマスターしていれば良いのです。さて、肝心の数学についてですが、どの高校でも数学III・Cの履修がほぼ終わる、11月~12月頃が最も重要な時期です。志望大学の過去問はもちろん、同レベルの大学の過去問を1日に3~4題くらいずつチャレンジしておくことが大切です。できなかった問題は、解答を見て納得しておけばよいのですが、論述式の答案の書き方などを、自分でも答案を書いて、しっかりトレーニングしておくべきです。できるようになった問題を何回も繰り返して解くよりも、できない問題に積極的にチャレンジして、できる問題のレパートリーを広げることに力を入れるべきです。塾・予備校に通っていて忙しい人でも、予備校講師が黒板でやって見せるのを眺めているだけでは、自力で解けるようになりません。自分の頭を使ってやってみることが大切です。この1日に解く問題の数が、4題から3題に、2題、1題と、センター試験が迫るにつれて減ってくるくらいにしておくべきなのであって、気がついてみたら1ヶ月間、2次試験用に1題も解いていなかった、ということがないように努力して欲しいと思います。正月明けの頃からは、「大学への数学」の日々の演習の問題だけでも良いからやっておく、あるいは微積分の計算練習を日に30分で良いからやっておく、ということを心がけるべきです。センター試験の準備中にも2次試験用に何がしかのことをやっておけば、論述式問題や微積分の感覚が頭の中から消えてなくなってしまうと言うことはありません。特に、難関国公立大学を目指す人は、センター試験の点数を多少犠牲にしても、論述対策を欠かしてはいけません。東大や東工大ではセンター試験の点数が加味されると言っても、2次試験のウェイトの方が高いのです。重要度の高い方を優先すべきだと考えてください。この時期、少し難しくなると手が止まってしまう、ということで、数学で伸び悩んでいる諸氏に、下記の本をお薦めしておきます。手を動かさなくても良いので、熟読してください。 CFV21大学入試問題サイトへ
2006.11.15
コメント(0)
-

センター試験「物理」必勝法
昨日の日記で、「センター試験・数学」の勉強法について書きました。きょうは、「センター試験・物理」について書いておきます。数学では、充分な準備をしておかないと失敗しやすい、というようなことを書きましたが、センター物理では、数学ほどに恐怖感を持つ必要はありません。センター物理固有のクセ、とか、問題テーマと言えるものはありません。選択肢問題になっているという点を除けば、学校の定期試験とそれほど雰囲気が違うことはないと思います(高校の物理の先生が風変わりな人なら別ですが)。強いて言うならば、日常生活、時事的話題の中の物理現象がネタとしてよく取り上げられている、くらいのことだと思います。数学のように、時間との闘いになるということはまずないと言えます。複雑な計算も出て来ないし、単発的な問題が並んでいるので、連鎖反応を起こして、最初をミスしたばかりに大問全体を落としてしまうと言うこともありません。また、考え込んでしまうような難問もありません。難問が並んで平均点の低い年もありましたが、そういう例外的な年を除けば、しっかりと準備をして、落ち着いて取り組めば、高得点が狙えます。センター試験の準備をする上で最良の参考書は教科書です。教科書の例題と同じ問題や、同じ図やグラフが登場することもあります。最近の教科書は、色刷りでわかりやすいイラストがふんだんに入れてあって、昔の無味乾燥意味不明の教科書でちんぷんかんぷんだった私たちの頃からすれば羨ましい限りです。物理現象の説明や用語の意味などを、教科書でしっかり把握しておいてください。理系受験生にとって、今の高校物理のカリキュラムは非常に不幸な状況にあるので、教科書を授業で使わない高校の先生も多いと思いますが、センター試験向けには教科書をまず熟読すべきです。教科書に取り上げられている内容は、どの内容でも採り上げられる可能性があります。抜けのないように全般に渡って教科書の記述を理解するように心がけてください。ただし、物理は暗記した知識量を競う科目ではありません。細かい場合分けの一つ一つを暗記しようとすると頭に入り切らなくなります。基本法則をよく理解して、問題文に与えられた状況に基本法則を適用するとどうなるのかを、問題に合わせて考えることが大切です。用語などの知識を問う問題も出ますが、用語の数そのものが他の科目と比べて少ないのです。物理の基礎学力のある人なら、教科書の用語すべてをマスターするとしても、冬休みに2日程度充てれば覚えきれるくらいの分量です。物理は得点が勉強時間に比例する科目ではないので、暗記に走らないように、くれぐれも注意してください。ここ数年間、センター物理の範囲がかなり変化しているので、理系受験生は、センター物理の範囲しか勉強しない、ということではなく、各大学で実施される本試験のための勉強の一部分、という位置づけで、センター試験物理の準備をして欲しいと思います。その分、数学ほど入念にセンター用の準備をしておく必要はないと思います。試験の雰囲気は、'06年度の問題を眺めればつかめると思います。センター試験固有には、センター試験用の問題集を試験10回分くらい練習し、下記に掲げる大数編集部制作の「センター試験必勝マニュアル」を通読し、必要な部分について頭にたたき込んでおけば充分だと思います。あとは、本試験用の勉強をしっかりやっておいてください。センター試験では、細かい計算をさせない配慮から、公式の形から定性的に考えて解答が出せるような出題方法が工夫されています。'06年度の問題で言うと、火星表面と地表とで重力加速度の違いにより、鉛直上方投射された物体の高さのグラフを選ぶ問題がそうです。問題文に、「同じ初速度で」と書かれているので、投射時点での接線の傾きが火星と地球とで同じになるグラフを選べば何でもないのですが、感覚的にグラフを選ぶと失敗します。凸レンズを通過したあとの光の波面を選ぶ問題もそうです。物理法則に基づいてこうなるはずだ、というように考えて解答してください。物理の出題者は、選択肢を並べるときに、当てずっぽうでやったり、感覚的にやると、多分これを選ぶだろう(笑)、いかにもこの選択肢ではない、と、感じるようなものが実は理論的に考えると正解、ということを考えるのです。「うまい話には騙されるな」という感覚で、疑い深く選択肢を見てください。また、物理では、正負の違いを重要視してください。仕事をするのかされるのか、エネルギーは増えるのか減るのか、力の向きと運動の向きは同じか逆か、というようなことに神経を使ってください。ソレノイドに電流を流したときの磁力線の向き、磁石のS極、N極間に置かれた1巻きコイルに電流を流したときの回転の向き、1次コイルに電流を流すときに2次コイルに発生する起電力の向き、こうしたものは、'07年度には必ず出題されるはずなので、暗記して答を書くのではなく、いかなる状況でも、右ねじの法則、レンツの法則やフレミング左手の法則を使って、正しい結論が出せるようにしておいてください。センター物理は以前は出題予想がよく当たりました。全分野を均等に出題し、類題を2年続けないように、という雰囲気があったので、この2年間出ていないからこれだろうと思うとズバリでしたが、最近は、出題予想を意図的に外そうということを考えているようで、同一テーマを2年続けたり、出題分野を偏らせたり、ということが見られます。学校や予備校の先生の出題予想にあまり惑わされないように注意してください。上でも触れましたが、下記の東京出版「センター試験必勝マニュアル・物理」は、センター物理の準備をする上で、必要最小限の事項がコンパクトにまとめられていて役に立つと思います。ただ、この本は、センター試験で勝つことに焦点を絞っている本なので、教科書をまずしっかり読んで、ある程度、問題練習をしてから読んでもらえると良いと思います。 CFV21大学入試問題サイトへ2次試験対策もしっかりやっておきましょう。
2006.11.14
コメント(0)
-

センター試験「数学」必勝法
「大学入試センター試験」については、誤解している向きもあるので、注意点を書いておきたいと思います。「共通1次試験」、「センター試験」については、導入時には基礎学力を観る試験ということになっていましたが、毎年、解いている感じでは、とてもそのようには思えないのです。数学の試験が終わった途端に号泣が聞こえてきた、というような話も聞きます。軽く90点、運が良ければ100点、という感覚で無防備に試験場に臨むとヒドい目に遭います。まず、センター試験「数学IA」「数学IIB」については、数学の試験だと思ってはいけません。予備校の講評に、「良問揃い」などと、入試センターから情報をもらうために媚びを売るようなことが書いてありますが、とんでもありません。「悪問揃い」で、注意力、神経の緻密さ、神経の図太さの試験だと思ってください。特に、難関大学を目指し、高得点を狙う諸氏は、充分なトレーニングを積んで試験会場に臨むことが必要です。センター試験が「基礎学力を観る」という目的にそぐわないのは、複雑な文字計算や根号計算をさせる点にあります。120分くらいの充分な時間の与えられている本試験では、多少の失敗があっても時間内に気持ちを立て直すことができるのですが、センター試験の試験時間は60分です。あっと言う間に終わってしまう試験です。ワクにうまく入らない、とか、遠回りな解法でやってしまったために時間を食ってしまった、というような時に気持ちが動揺してしまうと、立て直す余裕がないのです。"2"と"3"を見間違えた、とか、"0"と"a"を見間違えた、というようなことが50点くらいの違いにすぐになってしまいます。英語や地歴公民の試験ではこういうことにはなりません。地歴公民の不得意な受験生が、数学を放ったらかしにして地歴公民ばかり勉強したら、倫理が90点で、数学が200点満点で90点、という笑えないことが起こります。センター試験の問題は、過去問をちょっとやってみればすぐにわかることですが、センター試験独特のクセの強い問題で、標準的な問題集には載っていないような問題が多いのです。個人的には、センター試験にはオリジナリティーは不要で、学校の定期試験でなじみのあるありふれた問題で充分だと思うのですが、全受験生に対して公平性を期す、ということのようで、風変わりな新奇性の強い問題が主になっています。ただし、高度な知識・技巧が問われることはないので、知識としては教科書で充分です。従って、過去問でセンター試験の問題の雰囲気によく慣れておく、ということが重要です。予備校が実施する模擬試験程度の経験では危険です。知識としては大したことはないので、練習問題が範囲に入っているか、とか、出題傾向が問題ではありません。複素数平面などを除いて、過去問をよく練習しておく必要があります。難関国立大学狙いの受験生ならば、本試験と追試験で、過去問5年分を数回ずつ、目覚まし時計で60分をセットして、週に数回、本番さながらに練習を積んでください。そのときに、以下の点に留意して欲しいと思います。1) 必ず、ミスした点を反省すること。 ミスの原因は何か?問題の読み違いか、計算ミスか、復習の不足か、時間不足か。 計算ミスであれば、どうして計算をミスするのか、文字の書き方や、計算のしかたまで含めて検討してください。 また、捨て問題にすべきやむを得ない問題もあります。面倒な空間ベクトルの計算をするのだったら、ワクが3桁だから、120度にしておけ、で、当たり、ということがあるのです。 一度ミスした点を再確認するためにも、必ず、どの問題も、忘れた頃に複数回やることを心がけてください。やりっ放しでは意味がありません。2) 大問のなかの最初の数問の易しいところでミスをしないように綿密に見直すこと。 センター試験の特徴として、はじめをミスすると連鎖反応的にその大問は全滅ということが起こります。 最初の部分で焦らず、後に響かないように大切に解答するクセをつけてください。 問題の読み違いがないか、条件を見落としていないか、確率の場合分けの不足がないか、放物線の凹凸の勘違いと言ったようなことがないか、チェックを必ず入れてください。3) 余白の使い方を練習すること。 計算するときに、数字を大きく書くクセのある人は、消すか別のページに書かないと次の計算ができない、ということが起こります。 また、あっちに書いたり、こっちに書いたりする人は、見直しができないことになります。 小さな字で、後から見直せるように、左スミからきちんと書くクセをつけてください。 また、速く字を書く練習もしてください。鉛筆の持ち方も重要です。鉛筆を強く握るクセのある人はどうしても計算が遅くなります。4) メンタル・トレーニングを考えること。 試験会場で、ワクにはまらなくなった、気持ちが焦って計算が進まない、確率の場合分けができない、などの状況を想定して、自分の気持ちをどうやって落ち着けるか、おまじないの文句を考えておいてください。 私の頃には、「メアリー・ポピンズ」という映画に出てきた、スーパー・カリフラジ・リスティック・イクスピアリ・ドウシャスとか言うおまじないがありました。 どんどん気持ちを切り替えて、先へ進み、別の問題をやってから戻ってくる、というような対処も考えてください。5) 計算方法・解法の工夫をすること。 より簡便で短時間に解決できる解法を工夫してください。 ワクには整数しか入らないので、場合によっては、計算するよりも、正確にグラフを書いてマス目を数えた方が速い、というようなこともあります。 数列で一般項を聞かれていても、n=1,n=2と代入すると答がわかってしまう場合もあります。隣をのぞくのはルール違反ですが、解法は問われていない、何でもあり、ということも頭に入れておいてください。以上のような練習を効果的に行うために、仲間同志数人で、いっせいに過去問に取り組んで、お互いの問題点を指摘し合いながら(「いじめ」はだめだよ)、反省点を共有していくとよいと思います。不足している知識を補いつつ、練習が進んできたら、下記の東京出版「センター試験必勝マニュアル」を熟読しておくと良いと思います。コンパクトに必要最小限のセンター用の技巧が並んでいて参考になるでしょう。 CFV21大学入試問題サイトへ2次試験対策もしっかりやっておきましょう。
2006.11.13
コメント(0)
-
CFV21の解答方針
きょうは、ライブドア・ブログの方では、昨年の東大数学前期の第2問を再掲しました。元々長くてライブドア・ブログの限界サイズを超えてしまうので、削ってかなり短くしました。逆に説明の抜けている点は補足しました。最近は、東大も他大学と同様、若干易しめですが、この問題は、近年の前期の問題では最難問です。複素数平面の問題で、現在の高校の範囲外なのが残念ですが、歯ごたえのある重量級の問題です。実際に試験会場で思いつけるかどうかは別として、もっと簡単に解く方法が、例えば旺文社入試問題正解などに出ています。ここでは、多少の紆余曲折を経ても充分に時間内に解答し終えることの可能な方法を採用することにします。CFV21大学入試問題サイトへ
2006.11.13
コメント(0)
-
東大入試問題を再掲します
きょうから暫くの間、ライブドア・ブログの方で、昨年'05年度の問題を東大の問題から、再掲示していきます。問題文を本来の問題文に変え、説明文を多少修正し、基礎事項が充実したのに合わせて、リンクを張り直していきたいと思います。今後、物理の基礎事項のブログが混じりますが、数学と物理は本来1科目であって、敢えて別々に考えなくてもよいのではないか、ということと、最近、物理を選択する高校生が減っていることへの警鐘の意味を込めて、このようにします。物理が得意で、物理の基礎事項を見直す必要のない方、入試で物理を必要としない方は、読み飛ばしてください。CFV21大学入試問題サイトへ
2006.11.12
コメント(0)
-
こちらも再開します
前回の書き込みより、2年近く経ってしまいました。ライブドア・ブログで展開している大学入試ブログのうち、「数学」の方の基礎事項の入力が一通り完了しましたので、こちらにも、書き込んでいきたいと思います。ライブドア・ブログ(FC2ブログをミラー・サイトに使っていますが)では、入試問題そのもの、数学・物理の基礎事項そのものを取り上げ、こちらのブログには、経験上から言える難関大学チャレンジの勉強法、試験問題の講評・考察、入試制度への意見などを書いていきたいと思っています。年内は、高3・高卒生の方に向けて、センター試験への対応方法、2次試験への対応方法、高1・2生の方に向けて、難関大学にチャレンジするに当たっての考え方などを書いていこうと思います。CFV21大学入試問題サイトへ
2006.11.11
コメント(0)
-
センター試験数学IIBの検討(その4)
複素数では、教科書に様々な公式・基礎事項が書かれています。それらの有機的な関係が理解できずに複素数を苦手にする受験生が多いようです。しかし、センター試験でも国公立大学の2次試験でも、通り一遍に理解してしまえば、それほど奥深いわけではなく、図形的なことがらと複素数の関係式との間の結びつきをつかめるようになれば、意外と点数の取り易い分野なのです。受験生が井の中の蛙状態になり、ちょっと手を伸ばすだけで理解できる分野、実は奥が深くて点が取りにくい分野にだけ手を出して、実は点が取りやすいのに身の回りに存在しないようなものに関心を示さないのは残念です。新しい分野にどんどん首を突っ込んで行く気持ち、好奇心、チャレンジ精神をもっと持って頂きたいと思います。但し、この分野は、来年度以降はセンター試験の分野からは外れます。来年度からは、複素数の図形的応用面は2次試験でも原則出題されないはずです。この問題自体は、部分的に無意味な問題が含まれていますが、基礎事項だけで得点の取れるセンター試験の問題のレベルとしては適切だと思いますが、もう少し興味を持って解けるような題材的工夫が欲しい気がします。なお具体的な各問題の内容検討を、こちらに書き込んでおきました。
2005.01.26
コメント(0)
-
センター試験数学IIBの検討(その3)
引き続きセンター試験数学IIBの内容の検討を行います。第3問平面ベクトルの基礎問題です。ほんのちょっとした数学的センスと、ベクトル計算、内積計算、垂直なベクトル同志の内積は0になるという基礎事項のみで回答できますが、計算は、根号計算・分数計算が混じるので、かなりややこしい計算になります。慎重に計算することと、検算をしっかりやることが大事です。しかし、あまり丁寧すぎても時間が足りなくなる恐れがあります。良い問題とはとても言えません。もう少し、計算をラクにして、数学的な考え方、図形的考察をベクトルの関係式に転換するような技術を身につけているかを見るような問題を工夫すべきだと思います。スタートのところは、頂点Aと対辺BCの中点を結ぶ線分が辺OPと平行になり、Aのy成分とA1のy成分が等しくなることに気づけばちょっとしたベクトルの成分計算をするだけです。また、Bのx成分とACの中点のx成分も等しくなります。時間的に厳しい数学IIBでは、これにできる限り早く気づくことが重要で、気づくのが遅れると満点は難しくなります。ここが突破できればあとは、一本道です。誘導に乗ってミスをしなければ完答が充分に狙えます。東大京大東工大などを目指す諸君は、この問題を10分程度で軽く完答できるくらいの計算力が必要です。速さだけでなく、俊敏な着想力も必要です。検算をどのタイミングでどのように行うかという戦略も必要です。途中計算をあとで見直しやすく書く習慣が身に付いているかということも問われているのです。なお具体的な各問題の内容検討を、こちらに書き込んでおきました。
2005.01.25
コメント(0)
-
センター試験数学IIBの検討(その2)
引き続き、センター試験数学IIBの検討をしてみます。第2問前半は放物線のグラフに関する問題で頂点を求め、頂点の座標を媒介変数を使って表した後、媒介変数を消去して、頂点の軌跡を求める問題だが、平凡すぎてつまらない。やはり軌跡が円になるか、ならなくても円に関する問題の方がよいと思います。ここでは、積分の問題につなげるために2次関数が選ばれたのだと思いますが、無理につなげる必要もないと思います。ABに分けて、円に関する図形的問題と、積分の計算問題と別問題で構わないと思います。放物線の位置関係のグラフを選ばせる問題も、数学I分野なのではないかと思います。位置関係を考えさせるなら、2円の位置関係か円と直線の位置関係を問うべきです。結果的に数学IIの図形と方程式の分野の内容が実質的にほとんど問われていないことになってしまいました。最後にとってつけたように積分の計算問題がついていますが、定積分の端点が分数になっていて計算がやりづらく、ミスの誘発しやすい問題で、積分の計算方法の基礎を問う問題とは言えないと思います。計算方法の修得をうながす問題にするなら、端点の値は1とか2のような簡単な整数とすべきです。面倒な計算にも耐えるような忍耐力・持久力をみるのは各大学ごとの本試験の課題とすべきです。端点を分数や根号つきの数などにすると、計算結果が枠にはまらないような事になることが多く、精神的に弱い受験生ではパニックに陥りやすいのです。センター試験数学では、試験時間が1時間と短く、精神的に立ち直れないうちに試験が終了してしまい、試験終了時に泣き出すような受験生もいるという話も聞きます。センター試験の計算問題については、計算手法を習得しているかをみるようなものに方針を転換すべきだと考えます。なお具体的な各問題の内容検討を、こちらに書き込んでおきました。
2005.01.22
コメント(0)
-
センター試験数学IIBの問題について
第1問[1] 最初の部分は、2点間の距離の公式を用いるか、余弦定理を使いますが、基本的です。その後、半角の公式を用いて式変形しますが、結果の形が書かれているのでとまどうこともないでしょう。さらに、文字の置き換えにより、2倍角の公式を用いて2次関数の形に変形します。場合分けもしますが、この辺も一本道で、ケアレス・ミスに気をつけるだけです。2次関数になったあとは、平方完成してグラフに書けば、最小・最大はすぐにわかります。教科書をしっかりやってあれば、特殊な技術は不要で、計算も複雑ではないし、センター試験の趣旨からして妥当な問題だと思います。[2] これは見ただけで敬遠してしまう受験生がいたと思いますが、対数を考えて、対数の基本を使って式変形し、何とか大小を比較しやすい2数の形に直すことを目標にします。結果が見えないのでやりにくいと感ずるかも知れません。ですが、途中までは式変形の結果が書かれているので誘導通りに式変形して行くだけです。計算がとくに複雑ということはありません。特に最後でbとcの大小関係を比較するところで、どのように問題文のヒントを使うのか、考え込んだ受験生もいるかも知れません。対数の基本ができていれば充分に解答可能でありながら、受験生の意欲の差で差がつく良い問題だと思います。ただ、参考書などをしっかり勉強していれば、参考書によく出ているタイプの問題であり、受験技巧でこなすことも可能です。なお具体的な各問題の内容検討を、こちらに書き込んでおきました。
2005.01.19
コメント(0)
全58件 (58件中 1-50件目)