全214件 (214件中 1-50件目)
-
問い39.早とちりに注意。^^
太郎君のサイフは、今は何も入っていません。が、明日から、お母さんが毎日100円ずつ入れてくれることになりました。太郎君は、おやつに60円のキャラメルを1日1箱買うことにしました。ただし、サイフに500円以上ある日は、500円の豪華なアイスクリームをキャラメルの代わりにに買います。太郎君が5回目にアイスクリームを買うのは何日後でしょう?^^
2007.10.17
コメント(141)
-
問い38.ジュースの空き瓶
ジュースの空き瓶5本を持っていくと、新しいジュース2本に交換してくれるお店があります。100本買うと、何本のめるでしょう?また、200本以上飲むためには、最低何本買えばよいでしょう?
2007.10.16
コメント(1)
-
入門編、問い13.袋詰め。
5人の女の子がプレゼントのクッキーを袋に入れていきます。5分間で5袋のクッキーを袋詰めできます。では、50分間で50袋のクッキーを袋詰めするには、何人の女の子がいればいいでしょうか?^^
2007.10.12
コメント(2)
-
入門編、問い13.200gの砂糖
ここに砂糖が1kgあります。この砂糖を200gと800gに分けたいのですが、天秤が1台と50gの分銅が1つしかありません。天秤を3回使うだけで、200gと800gに分けてください。^^
2007.10.11
コメント(3)
-
入門編、問い12.何秒で完了?(間の数)
幅1cm、長さ58cmの細長い紙テープには、それを1平方cmずつの正方形に切り分けれるように線が入っています。ある少年は1秒間に1つの線をはさみで切ることができます。この少年が、58の正方形を切り取るのに何秒かかることになるでしょうか?ただし、まとめ切りはせずに、1つ1つ切っていくこととします。^^
2007.10.11
コメント(3)
-
入門編、問い11.ビルの階段(小学生のお子さんにどうです?^^)
ビルの1階から8階まで歩いていきます。さて、1階から2階に行くまでの何倍歩くことになるでしょう?^^
2007.10.11
コメント(1)
-
入門編、問い10.どんだけ~。^^
2人の兄弟が、お母さんからもらったクッキーを同じ数ずつ分けました。弟が食べ終わった後、兄が「ぼくはおなかがいっぱいになったので、残りをあげるよ。」といい、9個のクッキーをくれた。弟はそれも食べました。弟は、兄よりどれだけ多く食べたのでしょう?
2007.10.11
コメント(2)
-
論理の窓、問い9.宝を取り出せ。
黒丸が宝物で、白丸が爆弾です。○○○●○○○の順番で透明なホースに入っています。この爆弾はホースの中で動いているだけでは爆発しませんが、外に出たとたん爆発します。爆発すると、宝は木っ端微塵になってしまいます。さて、うまく宝をとりだすことができるでしょうか?ただし、ホースの中で2つの玉を入れかえることはできません。^^
2007.10.10
コメント(1)
-
問い37. 10個の石
なぞなぞっぽいですが。^^;ここに10個の石があります。これを4個ずつ、まっすぐに5つ並べてください。^^
2007.10.10
コメント(2)
-
問い36
例のように、ある整数のすべての位の数をかけ合わせて、その答えが1桁になるまで繰り返します。例 99→9×9=81→1×8=8 73→7×3=21→2×1=2最後の答えが6になる2桁の整数は、全部で何個あるでしょう。これは慶応の中等部の入試(2007)で出されたものです。^^
2007.09.28
コメント(3)
-
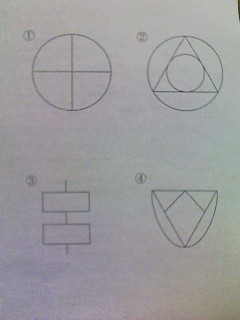
問い35.一筆書き
次のうち、一筆書きができるのはどれでしょう?^^
2007.09.28
コメント(2)
-
問い34の答え
(1)の答え 実は、7×7=49、49×7=343、43×7=301、01×7=07となり、7を繰り返しかけたときの下2けたの数は、07,49,43、01、07、・・・・の繰り返しになります。したがって、2007個かけても、2007÷4=501・・・3なので、3番目になるだけなので、十の位は4です。^^(2)の答えさて、6×6=36、36×6=216、16×6=96、96×6=576、76×6=456、56×6=336なので、6を繰り返しかけると、十の位は、最初の0を除くと、3、1、9、7、5の繰り返しになります。ここで、5*9は、5の倍数なので、求める数は周期の4番目の7であることがわかります。
2007.09.24
コメント(2)
-
問い33の答え
はじめの状態 ある牧場(A,B,C,D)、別の牧場(なし)1回目 Aの馬とBの馬で移動する(2分) ある牧場(C,D)、別の牧場(A.B) そして、Aの馬でもどる(1分) ある牧場(A,C,D)、別の牧場(B)2回目 Cの馬とDの馬で移動する(9分) ある牧場(A)、別の牧場(B,C,D) そして、Bの馬でもどる(2分)3回目 Aの馬とBの馬で移動する(2分) ある牧場(なし)、別の牧場(A,B,C,D) 16分で移動完了。^^
2007.09.22
コメント(2)
-
パターン化ということについて、考えてみる。
学級通信チャレンジさんより、パターン化ということについて、話題をふっていただいたので、少し、考えてみようと思う。^^パターン化というと、一番先に思うのは、公式である。パターン化=公式化と考えていいだろう。私はパターン化=公式化が一概に悪いとは思わない。むしろ、パターン化=公式化をいろいろと進めてきたことによって、とても考えやすくなってきたと思っている。しかし、公式の意味も理解しないまま、とりあえず、公式にあてはめて答えを出すというやり方では、百害あって一利なし、とも思っている。たとえば、円周の公式や円の面積の公式がある。これらを丸暗記させて、問題を解かせるのは単なる計算練習以外の何者でもない。そんなことより、どうして、直径に円周率をかけると円周が求まるのか?とか、半径×半径×円周率=円の面積という公式が、どうして成り立つのか?をきちんと考えさせることの方が大切であろう。それを理解できてから、パターン化=公式化して覚えるとよい。ある小学校の授業で、あきれたことがある。そこでは、「長方形の面積=たて×よこ」と教え、「よこ×たて」で計算したら、すべて間違いにされてしまうのだ。いつから、こんな教え方がされるようになってしまったのだろうか?これこそ、パターン化の典型であろう。こんな教え方が、現在でもその小学校ではまかり通っている。このような公式化、パターン化は、子供たちに考えることを止めさせ、ただ丸暗記を強制するだけの、とんでもないものだ。パターン化そのものが悪いのではなく、その教え方に問題があると言わざるを得ない。これは、小学校だけではなく、中学校も高校も多かれ少なかれ抱えている問題である。公式を丸暗記させてしまうのは、とてももったいない話だ。公式には、考え方のエッセンスがいっぱい詰まっている。公式(パターン)が、どうやってできているのか?を知るだけでも、とても面白く、考えることが楽しくなるはずなのに、本当にもったいない話だと思う。
2007.09.11
コメント(9)
-
問い34.十の位はいくつ?
同じ整数を繰り返しかける計算をします。2×2×2を2*3、3×3×3×3×3を3*5とそれぞれ表します。さらに、(4*3)*2=(4×4×4)*2=64*2=40964*(3*2)=4*(3×3)=4*9=262144 と計算します。(1)7*2007 の十の位はいくつでしょう?(2)6*(5*9)の十の位はいくつでしょう?これは、ある中学校の入試問題なのですが、2007とか、5*9なんかには、びっくりしてしまいますよね。^^;でも、直接計算しなくてもうまい方法があるのです・・・
2007.09.11
コメント(5)
-
問い33.手際のいい仕事
ある牧場から、別の牧場まで、馬たちを移動させなくてはなりません。馬は4頭で、別の牧場まで走るのに、Aの馬は1分、Bの馬は2分、Cの馬は5分、Dの馬は9分かかります。一人のカウボーイが、4頭の馬を運ぼうとしています。ただ、乗った馬ともう1頭しか同時に運ぶことができません。行き来は、馬に乗ってします。馬を連れて行くときは、おそいほうの馬の時間に合わせなくてはいけません。たとえば、Aの馬とDの馬で行くと、9分かかることになります。このカウボーイは、「16分ですべての馬を別の牧場に運ぶ事ができる。」と豪語します。さて、このカウボーイは、どのように馬を移動させたのでしょう?^^
2007.09.08
コメント(2)
-
論理の窓問い8の答え
さて、三人兄弟のうちの真ん中の気持ちになって、考えてみましょう。^^目を開けると、兄と弟2人は白い帽子をかぶっています。そこで、考えます。 「もし、自分が赤い帽子をかぶっていたとしたら、・・・」 兄には、1人が白で、1人が赤と見えるはずです。そのとき、兄は、考えるはずです。「もし、自分が赤をかぶっていれば、一番下の弟は、2人の兄が赤い帽子をかぶっているのが見えるのだから、すぐに白と答えるはずだ。しかし、答えない。ということは、自分は白だ。」と考えて、白だというはずなのに、兄は何も言わなかった。ということから、私のかぶっている帽子は赤ではなく、白だと気付いた。兄と弟も同じように考えたようで、3人同時に「白だ。」と答えることになった。^^
2007.09.08
コメント(3)
-
論理の窓問い7の答え
二人は、お互いの帽子を見た時に、白だとわかりました。^^赤い帽子は1つしかありません。 「もし、自分が赤い帽子をかぶっていたら、頭の良い相手は、すぐに自分は白いとわかっていうはずだ。しかし、何も言わなかった。ということは、自分は赤い帽子をかぶっていない。だから、白だ。」 と考えて、二人とも同時に「白だ」と言ったのでした。^^
2007.09.08
コメント(0)
-
論理の窓問い8.頭の良い3人兄弟
問い7の3人版です。^^;ある国に頭の良い三人兄弟がいました。王さまが3人を呼んで、問題を出しました。「ここに赤い帽子が2つと白い帽子が3つある。今からお前たちは目をつぶって、帽子をかぶらされる。その後目を開けて、自分の帽子の色は何色かあてるのじゃ。ただし、見えるのは相手の2つの帽子の色だけで、お互いに帽子の色を教えあってはいけない。」そして、王様は3人ともに白い帽子をかぶせました。目をあけた三人は、じっと考えた後、同時に「私がかぶっているのは白い帽子です。」と答えました。どうしてわかったのでしょう?^^
2007.09.03
コメント(4)
-
論理の窓。問い7.頭の良い兄弟。
これも有名なので、聞いたことがある人もいるかもしれないですね。^^では、問題です。昔、ある国にたいへん頭の良い兄弟がいました。王様が兄弟をお城によんで、問題を出しました。「ここに、赤い帽子1つと白い帽子2つがある。今から、お前たちは目をつぶって、帽子を1つずつかぶらされる。そのあとで目を開けて、自分の帽子の色をあてなさい。ただし、見えるのは相手の帽子の色だけで、もちろん相手に教えてもらってはいけない。」そして、王様は二人とも白い帽子をかぶせました。目を開けた二人は、しばらく考えて、二人同時に「私のかぶっているのは、白い帽子です。」と答えました。どうして、わかったのでしょう?^^
2007.09.02
コメント(3)
-
問い32.分銅の重さの答え
答え左の皿 右の皿 果実果物 1kg 1kg果物+1kg 3kg 2kg果物 3kg 3kg果物 3kg+1kg 4kg果物+3kg+1kg 9kg 5kg果物+3kg 9kg 6kg果物+3kg 9kg+1kg 7kg果物+1kg 9kg 8kg果物 9kg 9kg果物 9kg+1kg 10kg果物+1kg 9kg+3kg 11kg果物 9kg+3kg 12kg果物 9kg+3kg+1kg 13kg
2007.09.01
コメント(0)
-
問い31.蛸犬鶏算の答え
答えは、くまのすけさんのおっしゃるとおり、7通りあります。蛸を●、犬を■、鶏を▼としましょう。^^合わせて24匹、足の数が102本なので、●+■+▼=248●+4■+2▼=102 ● ■ ▼ 蛸 犬 鶏 2 21 1 3 18 3 4 15 5 5 12 7 6 9 9 7 6 11 8 3 13これが、答えの7通りです。^^
2007.09.01
コメント(0)
-
問い30.さいころの色塗りの答え
(1)答えを先に言うと、1通りです。^^さいころを3色に塗り分ける場合、となりあう色を違えるには、相対する面2面づつに同じ色を塗るしかありません。色の塗り方は、面を固定して考えると、(赤、青、黄)(赤、黄、青)(青、赤、黄)(青、黄、赤)(黄、赤、青)(黄、青、赤)の6通りが考えられます。でも、くまのすけさんがおっしゃる通り、さいころってどこから見てもいいんですね。^^だから、6面のどこから見ても、結局、全部同じことになってしまって、1通りしかないということになります。^^(2)これも答えを先に言うと、6通りになります。^^6面の色の塗り方は、同色を隣り合わせないで4色で塗る場合、2面、2面、1面、1面と塗るしかありません。2面に塗る色を決めると、自然と塗る場所も決まってしまうので、色だけ考えると答えが出てきます。4色のうち、2面をぬる2色の決め方は、(赤、青)(赤、黄)(赤、緑)(青、黄)(青、緑)(黄、緑)の6通りですから、結局、答えも6通りになります。図を入れた解説も後で、アップします。^^
2007.09.01
コメント(0)
-
入門編問い9.暗号
次の記号、■、▲、●は、それぞれ数字を表している。▲▲▲●●=17■▲●●●=33■■●=51だそうだ。^^それぞれいくらを表しているのだろう?
2007.09.01
コメント(3)
-
入門編問い8.小町算の答え
1-2-3+4+5=51+2+3-4+5=71+2-3+4+5=9いかかでしたか?^^入門編問い9入門編問い1問い1植木算
2007.09.01
コメント(1)
-
ブレークタイム1.の説明。
今度は、84×86で説明してみましょう。84×86の計算は、一の位どうしの積と、一の位と十の位の積と、十の位の積の和だから、 (一の位の積) 6×4(一の位と十の位の積)6×80(一の位と十の位の積)4×80(十の位の積) 80×80なので、6×4+6×80+4×80+80×80=6×4+(6+4)×80+80×80=6×4+10×80+80×80=6×4+((10+80))×80=6×4+90×80=24+7200=72246+4=10となるところがミソですね。^^ したがって、十の位が8なので、8×9=72、一の位の積が、6×4=24より、答えが7224となります。十の位以上が同じで、一の位の和が十の場合、すべて成り立つことになります。^^
2007.08.31
コメント(0)
-
ブレークタイム1.面白い計算方法1
75×75の計算をするとき、みなさんはどのようにしているでしょう?^^ふつうに筆算することが多いのではないでしょうか?そこで、ちょっと便利な簡単計算方法を紹介しましょう。^^十の位がどちらも7なので、7×(7+1)=56とします。一の位が5と5なので、5×5=25。したがって、答えは5625。ただし、これは十の位が同じ数で、一の位が足してちょうど10のときにしか利用できません。^^;さて、もうひとつ計算してみましょう。^^153×157=?15×16=240、3×7=21したがって、答えは24021です。^^「どうして、このようになるのか」については、また次回解説をします。^^;ブレークタイム1の説明
2007.08.30
コメント(3)
-
論理の窓、問い6の答え
舟は水面に浮いているので、水面が上がっても、ナワバシゴは船とともに上がる。したがって、相変わらず、一番下の段の棒がちょうど水面にさわっている。
2007.08.28
コメント(0)
-
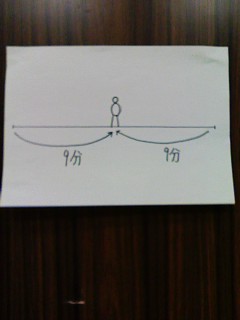
問い29.電車通りの答え
電車は等しい時間をへだてて、一定の速さで動いているので、もし、人が動かなければ、下の図のように、9分ごとに出会うことになります。人が時速4kmで動くことによって、10分ごとに追いこされ、8分ごとに出会うことになります。ということは、人の進む道のりの9倍が電車の進む道のりですから、4×9=36、つまり時速36kmが答えになります。^^もう少し、詳しく考えてみましょう。^^電車の時速をxkmとします。この図の全体の道のりは、時速xkmで進んだときの18分に当たります。したがって、x(km)の18/60倍に当たります。人が時速4kmで歩いたとき、10分ごとに追いこされ、8分ごとに出会うわけですから、その道のりの比は、時間の比と同じです。つまり、xの10/60(倍):xの8/60(倍)=10:8=5:4です。これが時速xkmと時速4kmの和と、時速xkmと時速4kmの差の比になるはずですから、(x+4):(x-4)=5:45(xー4)=4(x+4)よりx=36したがって、電車の時速は36km となります。^^
2007.08.28
コメント(0)
-
問い32.分銅の重さは?
その果物売りは、たった3つの分銅と天秤しか持っていないそうです。しかし、はんぱのない重さなら、1kgから13kgまですべて量れるといいます。さて、3つの分銅とは、それぞれ何kgの分銅なのでしょう?^^問い32.の答え問い1.植木算入門編問い1.論理の窓
2007.08.27
コメント(2)
-
問い31.蛸犬鶏算(江戸時代からの挑戦!)
今回は、江戸時代の数学者、村井中漸が書いた「算法童子問」からです。^^さて、江戸時代からの挑戦を受けてみませんか?^^「まな板の上に蛸、調理場から裏庭を見ると、犬と鶏が遊んでいる。板前さんが数えたら、合わせて24匹、足の数は102本であった。蛸、犬、鶏は、それぞれ何匹いるでしょうか?ただし、足の数は蛸8本、犬4本、鶏2本で、足の欠けたものはいなかったそうです。」これだけなのですが、ちょいとヒント、答えは一つじゃなさそうですね。^^
2007.08.25
コメント(2)
-
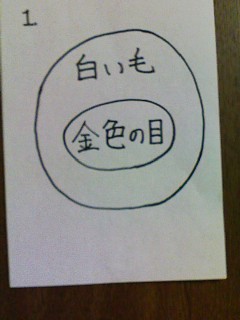
問い4.ちゃんと考えてるのは誰?の答え(論理の窓)
1.まず、「金色の目をしたシャム猫は、すべて白い。」について、考えてみる。この文が正しいとして、「白いと、金色の目をしている」と言えるだろうか?残念ながら、言えない。「金色の目は、すべて白い」のであって、「黒い目で白い」のがいたっていいのである。「白くても、金色の目とは限らない。」のである。逆にすると、正しくなくなる場合があるのだ。^^2.次に、「金色の目をしたシャム猫は、すべて耳が大きい。」について、考えてみる。これも、1.と同様のことが言える。つまり、「金色の目としてると、耳が大きい。」は正しいけれど、「耳が大きくても、金色の目をしているとは限らない。」3.「耳の大きいのは、すべて尻尾が長い。」についても同様である。「耳が大きいと、尻尾は長い。」と言えるが、「尻尾が長くても、耳が大きいとは限らない。」4.さて、ここで、2番と3番をまとめてみよう。「金色の目だと、耳も大きいし、尻尾も長い。」けど「耳が大きいと、尻尾は必ず長いけど、黒目かもしれない。」「尻尾が長くても、耳が小さく、黒目かもしれない。」のである。^^5.さて、1番をここに加えて、まとめてみよう。ちなみに、右の三重丸のほうが4(尻尾、耳、金色の目)で、左の二重丸が1(白い毛、金色の目)です。^^;a.「白くて、尻尾が長く、耳が大きい、金色の目のシャム猫」b.「白くて、尻尾が長く、耳が大きいけど、金色の目ではないシャム猫」c.「白くて、尻尾は長いけど、耳は大きくなく、金色の目でもないシャム猫」d.「白いけど、尻尾は短く、耳は大きくなく、金色の目でもないシャム猫」e.「白くないけど、尻尾は長く、耳が大きい。でも、金色の目ではないシャム猫」f.「白くないけど、尻尾は長い。でも、耳は大きくなく、金色の目でもないシャム猫」と分けることができる。さて、では、それぞれの発言を見てみよう。トシキ君「耳は大きいけれど、目が金色でないシャム猫は、すべて白い毛をしてるんだね。」これは、eのシャム猫が入ってないので、まちがい。カオリさん「白い毛をしているシャム猫は、すべて耳が大きいのね。」これは、cのシャム猫とdのシャム猫が入ってないのでまちがい。コウジ君「白い毛をしているけれど、目が金色でないシャム猫は、すべてしっぽが長いんだ。」これは、dのシャム猫が入ってないので、まちがい。サキさん「しっぽは長いけれど、白い毛をしていないシャム猫は目は金色でないのね。」実は、この発言が正しかったのです。いかがでしょう?だまされませんでしたか?^^論理の窓、問い5.数字の扉、問い1.植木算入門編問い1.
2007.08.25
コメント(0)
-
問い28.小町算3の答え
(1)12+3-4+5+67+8+9=100(2)12+3×45+6×7-89=100どうでしたか?うまくできたでしょうか?^^問い29.電車通り。問い1.植木算入門編問い1.論理の窓問い1.
2007.08.25
コメント(0)
-
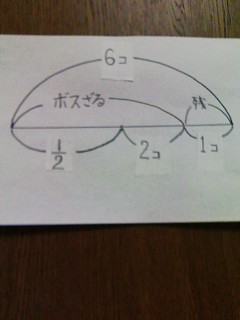
問い27.(2)の答え
ボスざるに半分と2個を取られたら、残りが1個になったのだから、半分は3個とわかるので、この全体は6個とわかる。番犬と出会い、半分と2個を落とした残りが6個だから、半分は8個とわかるので、この全体は16個。番人と出会い、半分と2個を落とした残りが16個だから、半分は18個とわかるので、全体は36個。したがって、もともと36個だったことがわかります。^^問い28.小町算問い1.植木算入門編問い1.論理の扉問い1.赤ワイン
2007.08.23
コメント(2)
-
問い6.ナワバシゴ
港から遠くないところに、舟が浮かんでいます。ふなべりからナワバシゴをたらしています。ナワバシゴは9段で、段と段の間がちょうど20cmあります。今日は海もおだやかで、波がひとつもありません。ナワバシゴの一番下の段の棒がちょうど水面にさわっています。これから、満ち潮になって、水が1時間ごとに10cmずつ上がってくるそうです。さて、今から5時間後には、水面はナワバシゴの何段目までくるでしょうか?^^論理の窓問い6.の答え論理の窓問い1.赤ワイン数字の扉問い1.植木算
2007.08.23
コメント(2)
-
入門編問い8.小町算
□の中に、+かーを入れて、式を完成させてください。^^1□2□3□4□5=51□2□3□4□5=71□2□3□4□5=9入門編問い8の答え入門編問い1問い1.植木算
2007.08.23
コメント(0)
-
問い31.数える。
1もしくは2を小さい順に左から並べて、ある整数を1と2のみの和として表すことを考えます。たとえば、5という整数については、1+1+1+1+1、1+1+1+2、1+2+2の3通り考えられます。このように、2006を1と2のみの和として表すとき、その表し方は何通り考えられますか?^^これは、2006年度のラ・サール中学の入試問題に出題された問題です。まともに数えると大変ですが、工夫をすると、案外楽に答えが出せそうです。^^
2007.08.23
コメント(3)
-
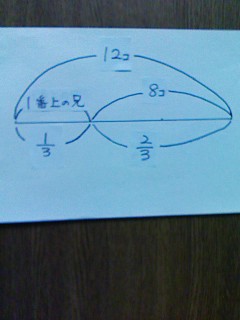
問い27.(1)の答え
1番上の兄が残りの3分の1を取った残りが8個なので、まず、残りの全体が12個とわかる。2番目の兄が取った後の残りが12個とわかったので、末っ子が取った後の残りは、18個とわかる。末っ子が取った残りが18個とわかったので、一番はじめの全体が、27個とわかる。問い27.(2)の答え
2007.08.22
コメント(2)
-
問い30.さいころの色塗り。
普通の立方体のサイコロがあります。まだ、面には何も書いていません。隣り合う面には、同じ色を塗ってはいけません。(1)このサイコロに、赤、青、黄の3色の色を塗ります。 さて、何通りの塗り方があるでしょう?^^(2)このサイコロに、赤、青、黄、緑の4色の色を塗るとき、 何通りの塗り方があるでしょう?^^ 問い30.の答え問い1.植木算入門編問い1.論理の窓問い1.
2007.08.22
コメント(2)
-
入門編問い7.クマのデート鶴亀算の答え
クマちゃんが毎分60mで歩いていったとすると、1800m÷60m=30分もかかる。着くのが、8時30分(10分の遅刻だ!これは彼女に怒られるな。クマちゃ~ん、ピ~ンチ!^^;)で、8時20分の時点では、クマちゃんはどこにいたかと言うと、家から、60m×20分=1200mの地点・・・・まだ後600mも残ってる。^^;毎分120mで走ると、1分に120-60=60m取り戻せるから、600mを取り戻すには、ちょうど10分走らなくてはならない。したがって、走った距離は、120m×10分=1200mでした。^^方程式を使った解も書いておきます。^^走った時間をx分とすると、残りの時間は(20-x)分。全部で1800m行くのだから、60x+120(20-x)=1800∴60x=600となり、x=10走った距離は、120×10=1200(m)入門編問い8.入門編問い1.問い1.植木算
2007.08.22
コメント(0)
-
入門編問い6.の答え
20枚すべて、50円切手を買ったとすると、全部で1000円。50円切手と80円切手の1枚分の違いは、30円。全部で、1450-1000=450円の違いがあるのだから、450÷30=15枚分の差がある。したがって、80円切手は15枚。^^50円切手は、20-15=5枚。連立方程式を使った解です。^^50円切手の枚数をx枚、80円切手の枚数をy枚とします。全部で20枚ですから、x+y=20・・・(1)金額は1450円ですから、50x+80y=1450・・・(2)(2)-(1)×50より30y=450∴y=15 x=20-15=5したがって、50円切手5枚、80円切手15枚。入門編問い7.クマのデート鶴亀算入門編問い1.問い1植木算
2007.08.22
コメント(0)
-
入門編問い5.サバンナで鶴亀算の答え
3000すべてがフラミンゴだとすると、足は3000本です。^^なので、4500-3000=1500本が余分にあります。フラミンゴとヌーの足の数の差は、3本ですから、1500÷3=500したがって、ヌーは500頭。フラミンゴは、3000-500=2500羽。別解です。連立方程式で解いてみます。フラミンゴの数をx、ヌーの数をyとします。全部で3000ですから、x+y=3000・・・(1)足の数は4500ですから、x+4y=4500・・・(2)(2)-(1)より3y=1500 ∴y=500x=3000-y=3000-500=2500したがって、フラミンゴ2500羽、ヌー500頭。^^入門編問い6.郵便局で鶴亀算入門編問い1.問い1.植木算
2007.08.22
コメント(2)
-
入門編問い4.鶴、亀、鶴、亀の答え
答えのアップ、遅くなりました。すみません。^^;では、答えです。^^もし、13が全部、鶴だとしたら、足は26本のはずです。^^全部で38本ですから、余分に38-26=12本も余分にあります。亀と鶴の足の差は、2本ですから、12÷2=66匹が亀とわかります。残りが鶴ですから、13-6=7、7羽が鶴とわかります。したがって、亀6匹、鶴7羽が答えです。^^別解連立方程式を作ってみましょう。^^亀の数をx、鶴の数をyとおきます。全部で13ですから、x+y=13・・・(1)足の数は38ですから、4x+2y=38・・・(2)(2)-(1)×2より 2x=12 ∴x=6、y=13-6=7 したがって、亀6匹、鶴7羽。^^入門編問い5.サバンナで鶴亀入門編問い1.問い1.植木算
2007.08.22
コメント(0)
-
入門編問い3.二倍、二倍。の答え
半分が2倍になれば、全体(1)になります。^^40日目に全体(1)をおおったのだから、その1日前が半分だったのです。したがって、39日目が答えです。^^喜文治さん、正解です。^^b入門編問い1.入門編問い4.
2007.08.19
コメント(0)
-
入門編問い2.の答え
入門編問い2の答えです。^^4+5=98-7=12×3=6やはりかけざんから、考えると簡単でしょう。2×3=6か、2×4=8しかありません。^^2×4=8だと、残りの1,3,5,6,7,9から足し算を作らなくてはなりません。しかし、できません。2×3=6が見つかったら、1,4,5,7,8,9で足し算と引き算をつくりましょう。この中で、足し算が成り立つのは、1+4=5と、4+5=9しかありません。したがって、2×3=6 4+5=9 8-7=1 とわかります。入門編問い1.入門編問い3.二倍、二倍。
2007.08.19
コメント(0)
-
入門編問い1.の答え
答えは次の通りです。^^1+4=52×3=6かけざんから、考えるとわかりやすいね。1の段は同じ数字になるので、無理!2×3=6しか使えないので、決まり!^^b入門編問い2へ
2007.08.19
コメント(0)
-

入門編問い7.クマのデート、鶴亀算。
今日は、クマのデートの日。^^クマの家から、クマの彼女の家まで、1.8kmあります。クマは今朝8時に家を出ました。(うきうき気分。^^)クマは物思いにふけりながら、分速60mの速さで彼女の家に向かいます。約束は8時20分。途中でハッと時計をみると、やばい時間になってる!間に合いそうにないので、分速120mで走りました。(ハアハア、ゼイゼイ)夏の暑さが応えバテ気味でしたが、ちょうど8時20分に着くことができました。(やったね。クマちゃん。)くまのすけさんの愛猫クマちゃん。画像、お借りしました。^^;さて、クマの走った道のりは何mでしょう?^^方程式を使わずに解いてね。^^
2007.08.19
コメント(4)
-
入門編問い6.郵便局で鶴亀算。
あやちゃんが、郵便局に切手を買いに行きました。50円切手と80円切手を合わせて、20枚買いました。全部で1450円でした。50円切手、80円切手をそれぞれ何枚ずつ買ったでしょう?^^方程式を使わずに解いてみてね。^^
2007.08.19
コメント(0)
-

入門編問い5.サバンナで鶴亀算。
サバンナの水飲み場。フラミンゴとヌー(ウシカモシカ)の群れがたくさんいてる。フラミンゴはすべて1本足で立っているとします。フラミンゴとヌーを合わせて、3000います。見えている足の数は、全部で4500。さて、それぞれ何匹づついてるでしょう?^^方程式を使わず、解いてみてね。^^
2007.08.19
コメント(0)
-
入門編、問い4.鶴、亀、鶴、亀。
オーソドックスな鶴亀算です。^^つると亀が合わせて、13います。足の数は全部で38本あります。つると亀は、それぞれ何匹いるでしょう?^^
2007.08.19
コメント(2)
全214件 (214件中 1-50件目)










