くぴんのブログ

プロフィール

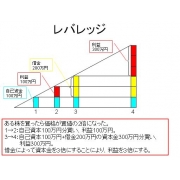
くぴん７４

フォローする

フリーページ

家電

(1)

バックナンバー

2024年11月
2024年10月
2024年09月

2024年08月
2024年07月

お気に入りブログ

DOW 44722.06 -138.2… New! どらりん0206さん

2024～25主力株概況3… New! みきまるファンドさん

楽天ラッキーくじ更…

じゃっかすさん

自分を愛することは… まりあのじいじさん
パワーアシストロボ… jhiranoさん

ニューストピックス

キーワードサーチ

▼キーワード検索

< 新しい記事

新着記事一覧(全4785件)

過去の記事 >

2012年01月02日

算数からはじめよう！数論

(2)

カテゴリ：本の紹介

【送料無料】算数からはじめよう！数論
価格：2,520円（税込、送料別）

１　割り算から合同式へ
２　素数と素因数分解
３　不定方程式ー方程式の製数解をさがす
４　合同式の発展ーフェルマーの小定理・オイラーの定理
５　平方数の和
６　連立合同式
７　平方剰余
８　連分数
９　連分数の応用ーπが無理数であることの証明

かつて、かの大数学者ガウスは「数論は数学の女王である」といった。
難しい数論を、具体的で簡単な計算例を豊富に入れて解説している。

第１章から第７章までは、合同式とその応用について書かれている。

ぼくは工学部の出身だが、高校でも大学でも合同式を習ったことがない。
大学院を出てから、人生に迷っていた時期に、通信教育で数学の教職課程をとろうとしていたときに初めて合同式というものを知った（単位はとりましたが、教職には就きませんでした）。

無限にある整数を、ある数で割ったときの余りで分類すれば、余りは割る数よりも必ず小さいので、限られた数に分類することができる。

例えば、どんな整数でも、3で割ったときの余りは0、1、2の3通りしかない。
5を3で割っても、3002を3で割っても余りは2である。

3002≡5 (mod 3)
5≡2 (mod 3)

上の式は、「3002と5は3を法として合同である」と読むのだが、意味は、3002も5も3で割ったと

これを使うと、すべての整数は、法とする整数で割ったときの余りが周期になっているかのように扱うことができる。

例えば、以下のような問題も簡単に解ける。

3^12を5で割ったときの余りはいくつか。

解)
3^12≡3^(3*4) (mod 5)

≡2^4 (mod 5)
≡16 (mod 5)
≡1 (mod 5)

よって1

ぼくが数学に魅せられる理由の１つは、このように、一見、まともに手をつけるととてもできないような問題が、見方を変えることによって簡単に解けるところにある。