PR
X
フリーページ
おすすめCD

DREAM THEATER

EXTREME

DEF LEPPARD

MR.BIG

METALLICA

MEGADETH

LOSTPROPHETS

HOOBASTANK

TRAPT

FOO FIGHTERS

EAGLES

System Of A Down
ローンの計算方法
橘玲
クレジットカードのしくみ
大切な言葉集
この世界を混乱に導く悪魔のルール
ETF140銘柄チャート画像取得マクロ
エクセルVBAで高速フーリエ変換
株・資産運用

1.株式会社の始まり

2.資産形成の方程式

3.利回りに対する理解

4.単利と複利

5.債券価格

6.キャピタルゲインとインカムゲイン

7.株式投資の投資戦略

8.BS(貸借対照表)とPL(損益計算書)の関係

9.リスクと不確実性について

10.72の法則

11.家賃から物件価格を推定する方法

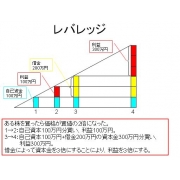
12.レバレッジ

13.ファンダメンタル指標

14.サラリーマンの生涯賃金

15.BPS+EPS×10の有効性

16. 裁定取引 (arbitrage)
fortran90で高速フーリエ変換
カレンダー
楽天ラッキーくじ更…
 New!
じゃっかすさん
New!
じゃっかすさん
2025年11月のまとめ。 New! みきまるファンドさん
DOW 47427.12 +314.6… どらりん0206さん
まさかの Maryu21さん
自分を愛することは… まりあのじいじさん
 New!
じゃっかすさん
New!
じゃっかすさん2025年11月のまとめ。 New! みきまるファンドさん
DOW 47427.12 +314.6… どらりん0206さん
まさかの Maryu21さん
自分を愛することは… まりあのじいじさん
キーワードサーチ
▼キーワード検索
カテゴリ: 本の紹介
1 体感してみよう!(素数/無理数/乱数/四元数/キス数/微分積分/二次方程式/三角関数/対数関数/デルタ関数/ベータ関数/テイラー関数/フィボナッチ関数/固有値/極座標/ラグランジアン/群論/トポロジー)
抽象的な数学の概念を、わかりやすく身近な例に置き換えて説明している。
ぼくにとって、わかりにくいもののひとつが、虚数だった。
数直線上で見ることができず、2乗して-1になる虚数単位i。
なぜ、こんなものを考えなきゃならないのかわからなかった。
しかし、考えてみると、マイナスの数というのも、ちょっとわかりにくい。
長さ、面積、体積、質量などは、マイナスになりえないし、目に見える形でマイナスを表現しようとするとちょっと戸惑う。
マイナスの数を実感するとすれば、お金の勘定がマイナスになるというのが一番実感しやすいと思うが、これはちょっとした抽象概念だ。
一番わかりやすく、しっくりくる数は自然数(1,2,3,…)だ。
そして、自然数どうしの四則演算(加減乗除)では、足し算と掛け算は結果が自然数となり問題ない。
しかし、引き算と割り算では、1-2=-1や、1÷2=0.5(1/2)となり、結果が自然数ではなくなる。
まず、自然数どうしの引き算の結果を定義するにはゼロと自然数にマイナスの符号をつけた数が必要となる。
そこで、自然数とゼロとマイナスの数をつけた自然数を合わせて整数と定義する。
これで、自然数どうしの引き算の結果はすべて定義される。
次に、自然数どうしの割り算では、循環小数と分数を導入すればすべての結果を定義できる。
ただし、ゼロで割ることだけは定義できない。
整数と分数と循環小数を合わせて有理数と定義している。
有理数どうしの四則演算では、結果は必ず有理数となり、数の体系として有理数だけ考えればいいように思える。
しかし、よく知られているように、円周率や面積2の正方形の辺の長さは有理数(循環小数)では定義できない。
そこで、有理数と無理数を合わせて実数と定義すれば、数の体系はすべて定義されたように見える。
しかし、x^1=-1の解は実数では定義できない。
そこで、この解を虚数単位iとして定義する。
しかし、実数の体系は数直線上で目に見ることができたのに対し、iは数直線上に出てこない。
2乗してはじめて、数直線上に現れる。
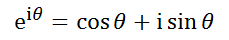
iとは、オイラーの公式でθ=90°(π/2)のときであり、虚数軸上にある。
i^2とは、iを90°回転するので、実数軸上の-1の位置にくる。
オイラーの公式は、波をうまく記述できるため、振動工学、電磁気学、量子力学などでは必須になる。
虚数が回転をあらわすことがわかると、本書にもある四元数が3次元空間の回転を定義するといわれてもなんとなくわかる気がする。
本書では四元数のおかげで、3Dゲームが楽しめることが紹介されている。
実数と虚数を合わせて複素数として定義する。
しかし、複素数まで考えたとしても、ゼロで割った結果は定義できない。
y=1/xのグラフでx=0の点が定義できないが、これが定義できればブラックホールのこともわかるようになるのだろうか?
数学は、荒唐無稽なことを書いているように思ったこともあったが、実は、宇宙を含めたこの現実世界を説明するためには必要不可欠であり、現代社会は数学の恩恵の上に成り立っていることを知ると興味が出てくる。
気楽に読めて、面白い本だった。


にほんブログ村
抽象的な数学の概念を、わかりやすく身近な例に置き換えて説明している。
ぼくにとって、わかりにくいもののひとつが、虚数だった。
数直線上で見ることができず、2乗して-1になる虚数単位i。
なぜ、こんなものを考えなきゃならないのかわからなかった。
しかし、考えてみると、マイナスの数というのも、ちょっとわかりにくい。
長さ、面積、体積、質量などは、マイナスになりえないし、目に見える形でマイナスを表現しようとするとちょっと戸惑う。
マイナスの数を実感するとすれば、お金の勘定がマイナスになるというのが一番実感しやすいと思うが、これはちょっとした抽象概念だ。
一番わかりやすく、しっくりくる数は自然数(1,2,3,…)だ。
そして、自然数どうしの四則演算(加減乗除)では、足し算と掛け算は結果が自然数となり問題ない。
しかし、引き算と割り算では、1-2=-1や、1÷2=0.5(1/2)となり、結果が自然数ではなくなる。
まず、自然数どうしの引き算の結果を定義するにはゼロと自然数にマイナスの符号をつけた数が必要となる。
そこで、自然数とゼロとマイナスの数をつけた自然数を合わせて整数と定義する。
これで、自然数どうしの引き算の結果はすべて定義される。
次に、自然数どうしの割り算では、循環小数と分数を導入すればすべての結果を定義できる。
ただし、ゼロで割ることだけは定義できない。
整数と分数と循環小数を合わせて有理数と定義している。
有理数どうしの四則演算では、結果は必ず有理数となり、数の体系として有理数だけ考えればいいように思える。
しかし、よく知られているように、円周率や面積2の正方形の辺の長さは有理数(循環小数)では定義できない。
そこで、有理数と無理数を合わせて実数と定義すれば、数の体系はすべて定義されたように見える。
しかし、x^1=-1の解は実数では定義できない。
そこで、この解を虚数単位iとして定義する。
しかし、実数の体系は数直線上で目に見ることができたのに対し、iは数直線上に出てこない。
2乗してはじめて、数直線上に現れる。
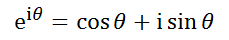
iとは、オイラーの公式でθ=90°(π/2)のときであり、虚数軸上にある。
i^2とは、iを90°回転するので、実数軸上の-1の位置にくる。
オイラーの公式は、波をうまく記述できるため、振動工学、電磁気学、量子力学などでは必須になる。
虚数が回転をあらわすことがわかると、本書にもある四元数が3次元空間の回転を定義するといわれてもなんとなくわかる気がする。
本書では四元数のおかげで、3Dゲームが楽しめることが紹介されている。
実数と虚数を合わせて複素数として定義する。
しかし、複素数まで考えたとしても、ゼロで割った結果は定義できない。
y=1/xのグラフでx=0の点が定義できないが、これが定義できればブラックホールのこともわかるようになるのだろうか?
数学は、荒唐無稽なことを書いているように思ったこともあったが、実は、宇宙を含めたこの現実世界を説明するためには必要不可欠であり、現代社会は数学の恩恵の上に成り立っていることを知ると興味が出てくる。
気楽に読めて、面白い本だった。

にほんブログ村
お気に入りの記事を「いいね!」で応援しよう
[本の紹介] カテゴリの最新記事
-
サトシ・ナカモトはだれだ? 世界を変え… 2025年10月26日
-
日本人拉致 2025年08月13日
-
最高の老後 「死ぬまで元気」を実現する5… 2025年07月12日
【毎日開催】
15記事にいいね!で1ポイント
10秒滞在
いいね!
--
/
--
© Rakuten Group, Inc.