PR
X
Calendar
Freepage List
カテゴリ: 語り
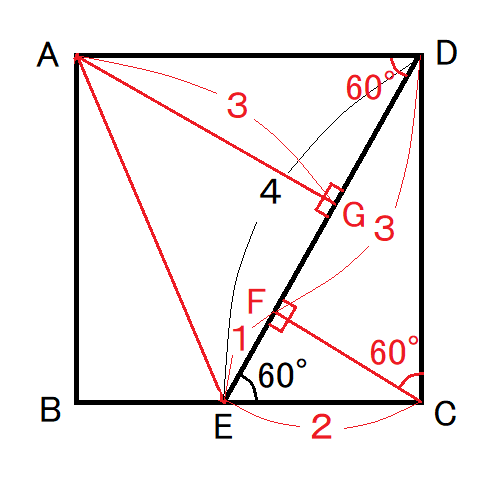
これは小学生にも分るだろうということで、方程式を解くようなことをせずに解きましょう。
ポイントは、補助線をどう引くかによって、自ずから答えが出てきます。
点Cから辺DEに垂線CFを引くと、∠DEC=60°なので、辺EC=辺DEの1/2=2、
ゆえに、辺EF=辺ECの1/2=1です。よって、辺DF=辺DE-辺EF=4-1=3となります。
次に、点Aから辺DEに垂線AGを引くと、三角形AGDは三角形DFCと同じ形(合同)であり、辺AG=辺DF=3である。
次に、点Aから辺DEに垂線AGを引くと、三角形AGDは三角形DFCと同じ形(合同)であり、辺AG=辺DF=3である。
よって、三角形AEDの面積は底辺DE×高さAG×1/2=3×4×1/2=6となる。
ここに、三角形AEDの面積は底辺をAD、高さをABと見れば、正方形ABCDの面積の1/2である。
したがって、正方形ABCDの面積=三角形AEDの面積×2=6×2=12となります。
したがって、正方形ABCDの面積=三角形AEDの面積×2=6×2=12となります。
お気に入りの記事を「いいね!」で応援しよう
【毎日開催】
15記事にいいね!で1ポイント
10秒滞在
いいね!
--
/
--
© Rakuten Group, Inc.











