JINさんの陽蜂農遠日記

素数探しのプロジェクトGIMP（Great Internet Mersenne Prime Search）という

パソコンのソフトウェア。

この計算に使われた式（メルセンヌ数）を最初に発見したのは、フランスの数学者の

メルセンヌという人物。

ソートイ教授は言う。「計算方法は、まず２の累乗をどんどん求めていく。

この場合、43,112,609乗。ここから『１を引く』と突然、素数に変わった。

これが2008年に発見された、初めて1,000万ケタを超えた素数だった」と。 

そしてつい2013に、1,700万ケタを超える大きな素数が発見されたと。

三角数であれフィボナッチ数であれ、すでに公式が知られたものであれば、

それを利用して10億ケタの数を探すことは力尽くできる。

しかし、素数に関しては完全なミステリー。

私たちは素数について、まだあまりにも無知なんだと。 

『物事があまりに複雑になりすぎた時は、そもそも正しい質問だったのか問い直すべきだ。』

これは素数の専門家、エンリコ・ボンビエリの言葉。

彼の言う通り、一時期、素数の問題はあまりにも複雑になりすぎていたと。

この「新たな問い」は15歳の少年によって投げかけられたのだと。

その天才の名は「ガウス」。

15歳の誕生日にプレゼントされた「対数の本」が、素数の世界に新たな幕を

開くことになったと。 

素数の並びの手がかりとして『素数階段』というものを考えていた。 

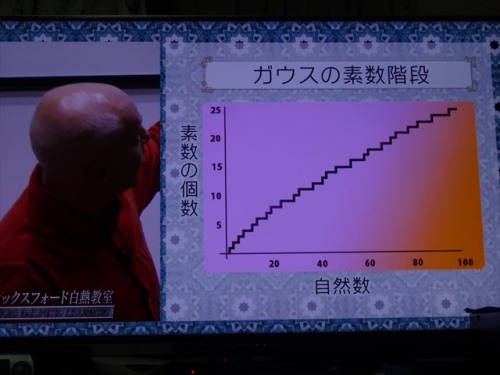
数字の列を書き、素数に出会ったとき階段を一段上がるというものをイメージしたの。

グラフを、ソートイ教授はこう説明する。

「ここでガウスは、これまで『一つ一つの段差がどこにあるのか』とこだわり過ぎていたと。

それよりも、この階段が『どのように増えていくのか？』、一步下がって大まかな傾向が

ないかを見てみることにした。

そうすることで、ガウスの前に『秘密のパターン』が浮かびはじめたんだ」と。

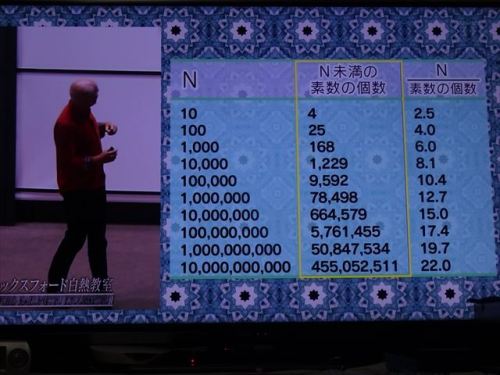
素数がどんどん大きくなるにつれて、パターンが見えてきたと。

１～１０の間に、素数は４個、割って２．５（Ｎ＝１０の時、Ｎ未満の素数の個数が４、

Ｎ／素数の個数＝２．５）という感じで調べていったと。

1～1,000までに168個の素数があるということは、およそ「6個に1個」の割合で

素数が現れると。

1万までなら、およそ「8個に1個」。10万までは、およそ「10個に一個」が素数。

10倍ずつの階段を上るにつれ、素数の現れる確率は下がっていっているのだと。

より正確に記すなら

1,000まで「6.0個に一個」、10,000まで「8.1個に一個」、100,000まで「10.4個に一個」

1,000,000まで「12.7個に一個」

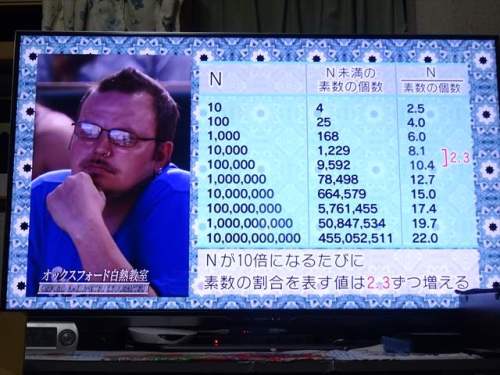
見えてきたパターンは、確率が低下する割合。

8.1から10.4への差は「2.3」

10.4から12.7への差も「2.3」

すなわちＮ／素数の個数がおよそ2.3ずつ増えていくことを突き止めた。

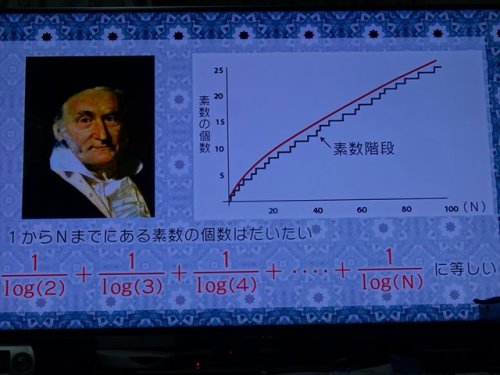
ガウスは対数を使い、「ガウスの素数階段」を大まかに表す式を作った。

この式で表すグラフで、どの範囲にどれくらいの素数があるか大まかに解るようになった。

これを見つけたのはガウス１５歳の時だ。

つまり、階段の「段差の高さ」は奇妙にも整って来たのだと。 

素数階段の近似式は下記の式で表されると。

ドイツの数学者ベルンハルト・リーマンが1859年に自身の論文

「与えられた数より小さい素数の個数について」において

リーマンの素数公式（Riemann's prime number formula）発表したと。 

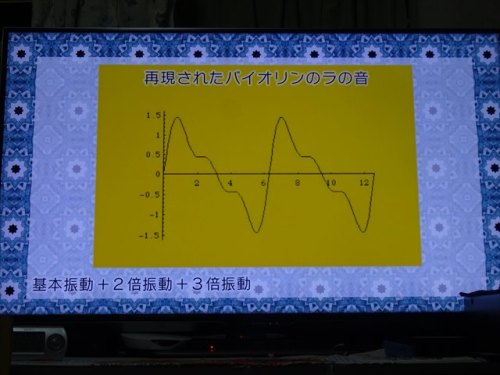
バイオリンという楽器の音の描くカーブは「ギザギザの波」。

それは、その音がたくさんの音（正弦波）が重なり合ってできているから。

バイオリンの出す正弦波は、バイオリンの弦の長さでそれが決まる。

これが基本振動となり、さらにそこに「倍音」と呼ばれるいくつもの音の波が重なり合う。 

そして『リーマン予想』の説明が。 

この辺から説明に付いていくのがしんどくなって来たのであった。

リーマンによる素数階段へのアプローチ。 

君たちがCDプレーヤーで音楽を聞くとき、その『音量』も大切だとソートイ教授。

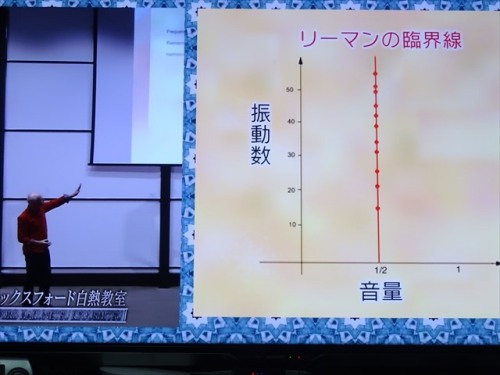
そこでリーマンは、波の振動数と音量を別のグラフにまとめた。すると驚くことに、

振動数はそれぞれ違うものの、波の音量はどれもまったく同じだった。

すべての音が魔法のように一直線上に並んでいたんだと。

てんでバラバラでも不思議でなかった、それぞれの音量。

ところが、それらは完璧に同じだったのだ。それは偶然の一致には思えなかった。

この直線はのちに、「リーマンの臨界線」と呼ばれるようになると。 

この辺は私の能力の限界以上で理解が出来なかったが教授の話は上記の如く。

リーマン予想について

ミレニアム懸賞問題（一億円問題）の一つ。2015年現在，未解決。

ミレニアム懸賞問題とは，100万ドルの懸賞金がかけられている数学の重要な7つの難問。

『ゼータ関数の非自明なゼロ点はすべて臨界線上にあるはずだ』と。

 これでは？？ 何のことかよく全くよく分からない。

素数の配列には何かの規則性があるはずだと考えていた数学者オイラーは、

次のような式を考えた。そして、この素数だけの式の値がある数に収束することを証明した。

あらゆる整数は一意的な素数の積として表わすことができるので、次のように変換できる。

素数という、一見ランダムに出現するかに見える数を無限にかけていくと、

完全な図形である円を表わす円周率が出現するのである。

素数という単純な数が、ま だ我々には理解できない宇宙やこの時空を構成している

基本的な法則と何らかの関係があるのではないかと想像され、ドキドキするではないか。

整数や素数の級数を眺めていても円周率が出てくるような気配はまったく感じられない。

しかし、突然πがでてくる。これには発見したオイラー自身も感動したと。

一 見ランダムに出現している素数に、何らかの規則性がありそうだということ。

それが円周率と関係しているらしい。

素数のまだ明かされていないその不規則さを、人類はすでに利用しているのだと。

インターネット上で安全性を確保する「暗号」がそれである。

たとえば、9999911という数字。この数は、ある２つの素数の掛け算の上に成り立っている。

そして、暗号を解くカギは、いわばその２つの素数。

「君がクレジットカードを使ってオンラインで買い物をしたいとする。

当然、カード番号の暗号化が必要だ。するとお店はこうした番号を送ってくる。

実際はもっと大きな数だが、この数とカード番号を使った暗号がつくられ、

お店とやり取りをする」とソートイ教授は言う。

もし、その暗号の数字を簡単に素数に分解できる公式があるとすれば、暗号化された数字は

あっさりと見破られてしまう。ところが素数にそうした式はまだ発見されていない。

ゆえに、素数が用いられた暗号を解くには、途方もない時間と労力が必要とされることになる。

これがインターネット上の暗号が安全だと考えられる理由であると。

ソートイ教授はさらに「とにかく、インターネット上の暗号は、まだ素数を求める式が

解明されていないことが前提になっている」と。

実際には下の写真のごとき巨大な数字が暗号化に用いられているのだと。 

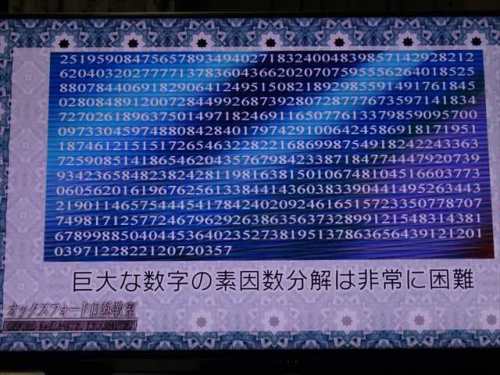
後半は殆ど理解できなかったが

ソートイ教授は数学者に対する最大の挑戦は「素数」であると。

「化学物質を分子や原子に分けることはできても、数字を素数に分解する簡単な方法は

まだ存在しない」とソートイ教授は言う。

それでもいずれ、リーマン予想でさえ証明される日が来るのだろうと。

「その成果そのものよりも、そこに至る進歩そのものが私たちの大きな財産になるだろう」と

ソートイ教授は確信する。

「私にとって、数学がまさに『生きた学問』であるのは、こうした問題のおかげだ。

リーマン予想や素数を追い求める挑戦こそ、私にとって数学の醍醐味だと感じている」と。

久しぶりに暫く使っていなかった頭をフル回転し録画放送を楽しんだ？？のであった。

次はフェルマーの最終定理を復習しようかとも。

フェルマーの最終定理とは

自然数 ｎ に対して、

 　 a ⁿ ＋ b ⁿ ＝ c ⁿ

を満たす自然数a,b,c  は存在しない。

a ² ＋ b ² ＝ c ² の場合は、 ３ ² ＋４ ² ＝５ ² ( a =3, b =4, c =5)と

いう解や多くの解が見つかるが、

n ≧ 3 (n が３以上）の場合、 つまり、 a ³ ＋ b ³ ＝ c ³ や a ⁴ ＋ b ⁴ ＝ c ⁴ や a ⁵ ＋ b ⁵ ＝ c ⁵ の場合は、 その式を満たす自然数 a 、 b 、 c は絶対に存在しないと。