PR
jinsan0716
『ＪＩＮさんの陽蜂農遠日記』にアクセスありがとう ございます。 このブログは、 陽：太陽光発電、 蜂：趣味の養蜂、 農：菜園、花、スロー＆アクティブシニアライフ、 遠：旅行、 を中心とした備忘録を兼ねた17年間にわたる毎日のブログ(雑記帳）です。 書き込んでいただける方は、写真下の『コメントを書く』から 気楽に、ご感想、ご意見ご質問等を書き込んでいただきたく。
Keyword Search
▼キーワード検索
Comments
私はイスラム教徒です@ Re:アイルランド・ロンドンへの旅(その131)： ロンドン散策記・アルバート記念碑（Albert Memorial)-2(11/06)
神神は言った: コーランで 『 (21) 人々…
私はイスラム教徒です@ Re:アイルランド・ロンドンへの旅(その122)： ロンドン散策記・Victoria and Albert Museum・ヴィクトリア&アルバート博物館-5(10/28)
神神は言った: コーランで 『 (21) 人…
【甥のステント挿入…
New!
Ｇママさん
2025年版・岡山大学…
New!
隠居人はせじぃさん
続日本100名城東北の… New! オジン0523さん
ムベの実を開くコツ…
noahnoahnoahさん
エコハウスにようこそ ecologicianさん
New!
Ｇママさん2025年版・岡山大学…
New!
隠居人はせじぃさん続日本100名城東北の… New! オジン0523さん
ムベの実を開くコツ…
noahnoahnoahさんエコハウスにようこそ ecologicianさん
Calendar
2023.07.18
カテゴリ： ＪＩＮさんの農園
整数の桁を並べ替えて、最大にしたものと最小にしたものとの差を取る。
この操作によって元の値に等しくなる数を『カプレカ数』と呼ぶ。
（カプレカ数とは裄を並ひ替えて、最大にしたものから最小にしたものの差を取った時
元の値に等しくなる数をカプレカ数と言う）
例えば
2023 2023−0223＝1800・・・・・・ダメ
8100−0018=8082・・・・・・ダメ
8820−0288=8532・・・・・・ダメ
8532−2358=6174・・・・・・ダメ
7641−1467=6174・・・・・・ ◯
となり、この後は 6174 が繰り返される。
どのような4桁の数でも最終的に 0 または 6174 になることが確かめられる
よって 6174は「カプレカ数」 。
カプレカ数を小さな順に並べる
0, 495, 6174, 549945, 631764, 63317664, 97508421, 554999445, 864197532,
6333176664,・・・・・・
「0」も含めてこれまでに 全部で20個のカプレカ数が見つかっているとのこと。
■ 3桁のカプレカ数が495のみであることの証明
証明
3桁のカプレカ数ｎの各桁の数字を大きい順に並べたものをabcとする。
0≤c≤b≤a≤9である。
このとき，
(100a+10b+c)−(100c+10b+a)=99(a−c)より
nは 99の倍数である。
したがって99の倍数かつ 3桁の自然数は9個しか存在しないため、
すべて実験して確かめてみると、カプレカ数495が導けます。
99 の倍数を1つずつ調べる。
198 →981−189=792 ダメ
297 →972−279=693 ダメ
396 →963−369=594 ダメ
594 →954−459=495 ダメ
693 →963−369=594 ダメ
792 →972−279=693 ダメ
891 →981−189=792 ダメ
990 →990− 99=891 ダメ
■ 2桁の場合
例えば 28 から始めて最大－最小のカプレカ操作を繰り返すと、
28： 82-28=54：54-45=9：90-09=81：81-18=63：63-36=27 ：72-27=45： 54-45=9
となり9 を中心に 9→81→63→27→45→9 の循環をする．
73の場合は
73：73-37＝36：63-36＝27：72-27＝45：54-45＝9：90-09＝81：81-18＝63：63-36＝
27：72-27＝45：54-45＝9
となりこれも、9 を中心に 9→81→63→27→45→9 の循環をする。
したがって、数が 2 桁の場合は、ある範囲の数を循環するが 2 つの混循環小数の形に似ている。
よって、 2桁のカプレカ数は存在しない。
■ 3桁の他の数字、例えば「523」で引き算操作を行ってみましょう。
532－235＝297
972－279＝693
963－369＝594
954－459＝495
右端の答えの部分、十の位の数字が全部「9」で、百の位の数字は上から順に
「6」⇒「5」⇒「4」とひとつずつ小さくなっており、一の位の数字は上から順に
「3」⇒「4」⇒「5」とひとつずつ大きくなっています。
また、ここに並ぶ3桁の数字は、一の位と百の位の数字を足すと9になるというも
特徴かもしれません。
■ 4桁の場合
4桁なので、0≦d≦c≦b≦a≦9
0≦d≦c≦b≦a≦9を満たす自然数 a、b、c、d<を使って、
N(大)=1000a+100b+10c+d
N(小)=1000d+100c+10b+a
と表すことができる。
よって、カプレカ操作を 1回行った数 N′は
N′=N大−N小=(1000a+100b+10c+d − (1000d+100c+10b+a)=999a+90b−90c−999d=
999(a−d)+90(b−c) となる。
さて、a－dは 1 と 9 の間の数値をとり、b－ cは 0 と 9 の間の任意の値をとり得るから、
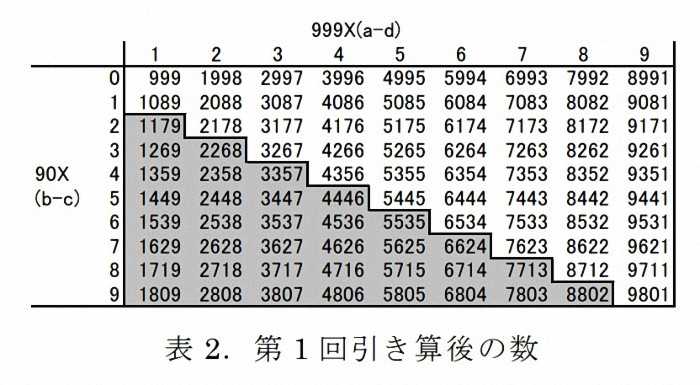
上記の形の数は全部で 90 個ある。そこで、確認のため数の表を作成した（表２）。
6,174に到達するのかを系統図で示したのが図 1である。これで、すべての 4桁の自然数が
6,174 に到達することが一目にしてわかるであろう。
この操作によって元の値に等しくなる数を『カプレカ数』と呼ぶ。
（カプレカ数とは裄を並ひ替えて、最大にしたものから最小にしたものの差を取った時
元の値に等しくなる数をカプレカ数と言う）
例えば
2023 2023−0223＝1800・・・・・・ダメ
8100−0018=8082・・・・・・ダメ
8820−0288=8532・・・・・・ダメ
8532−2358=6174・・・・・・ダメ
7641−1467=6174・・・・・・ ◯
となり、この後は 6174 が繰り返される。
どのような4桁の数でも最終的に 0 または 6174 になることが確かめられる
よって 6174は「カプレカ数」 。
カプレカ数を小さな順に並べる
0, 495, 6174, 549945, 631764, 63317664, 97508421, 554999445, 864197532,
6333176664,・・・・・・
「0」も含めてこれまでに 全部で20個のカプレカ数が見つかっているとのこと。
■ 3桁のカプレカ数が495のみであることの証明
証明
3桁のカプレカ数ｎの各桁の数字を大きい順に並べたものをabcとする。
0≤c≤b≤a≤9である。
このとき，
(100a+10b+c)−(100c+10b+a)=99(a−c)より
nは 99の倍数である。
したがって99の倍数かつ 3桁の自然数は9個しか存在しないため、
すべて実験して確かめてみると、カプレカ数495が導けます。
99 の倍数を1つずつ調べる。
198 →981−189=792 ダメ
297 →972−279=693 ダメ
396 →963−369=594 ダメ
594 →954−459=495 ダメ
693 →963−369=594 ダメ
792 →972−279=693 ダメ
891 →981−189=792 ダメ
990 →990− 99=891 ダメ
■ 2桁の場合
例えば 28 から始めて最大－最小のカプレカ操作を繰り返すと、
28： 82-28=54：54-45=9：90-09=81：81-18=63：63-36=27 ：72-27=45： 54-45=9
となり9 を中心に 9→81→63→27→45→9 の循環をする．
73の場合は
73：73-37＝36：63-36＝27：72-27＝45：54-45＝9：90-09＝81：81-18＝63：63-36＝
27：72-27＝45：54-45＝9
となりこれも、9 を中心に 9→81→63→27→45→9 の循環をする。
したがって、数が 2 桁の場合は、ある範囲の数を循環するが 2 つの混循環小数の形に似ている。
よって、 2桁のカプレカ数は存在しない。
■ 3桁の他の数字、例えば「523」で引き算操作を行ってみましょう。
532－235＝297
972－279＝693
963－369＝594
954－459＝495
右端の答えの部分、十の位の数字が全部「9」で、百の位の数字は上から順に
「6」⇒「5」⇒「4」とひとつずつ小さくなっており、一の位の数字は上から順に
「3」⇒「4」⇒「5」とひとつずつ大きくなっています。
また、ここに並ぶ3桁の数字は、一の位と百の位の数字を足すと9になるというも
特徴かもしれません。
■ 4桁の場合
4桁なので、0≦d≦c≦b≦a≦9
0≦d≦c≦b≦a≦9を満たす自然数 a、b、c、d<を使って、
N(大)=1000a+100b+10c+d
N(小)=1000d+100c+10b+a
と表すことができる。
よって、カプレカ操作を 1回行った数 N′は
N′=N大−N小=(1000a+100b+10c+d − (1000d+100c+10b+a)=999a+90b−90c−999d=
999(a−d)+90(b−c) となる。
さて、a－dは 1 と 9 の間の数値をとり、b－ cは 0 と 9 の間の任意の値をとり得るから、
上記の形の数は全部で 90 個ある。そこで、確認のため数の表を作成した（表２）。
この表で，
(a − d) ≧ (b − c)
であるから，左下の 36 個（網がけ）については意味のない数である．
次に、第 2 回引き算を実行するために、表2の数を大きい順に並べ変えると表 3 になる．
次に、第 2 回引き算を実行するために、表2の数を大きい順に並べ変えると表 3 になる．
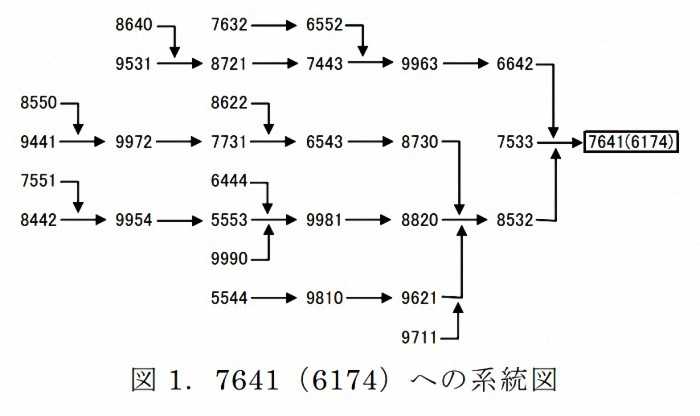
6,174に到達するのかを系統図で示したのが図 1である。これで、すべての 4桁の自然数が
6,174 に到達することが一目にしてわかるであろう。
最大 7 回で到達する
こともわかる．それにしても不思議なものだ。
■ 5桁の場合
53,955→95,553－35,559＝59,994
59,994→99,954－45,999＝53,955
(53,955 59,994)2つの数でグルグルと循環します。
よって、 カプレカ数は存在しない ということ。
■ 6桁の場合
549,945 → 995,544−445,599=549,945
631,764 → 766,431−134,667=631,764
とカプレカ数が 2個見つかっています 。
■ 7桁の場合 存在しません 。
■ ８桁の場合 2個 見つかっています 。
■ 5桁の場合
53,955→95,553－35,559＝59,994
59,994→99,954－45,999＝53,955
(53,955 59,994)2つの数でグルグルと循環します。
よって、 カプレカ数は存在しない ということ。
■ 6桁の場合
549,945 → 995,544−445,599=549,945
631,764 → 766,431−134,667=631,764
とカプレカ数が 2個見つかっています 。
■ 7桁の場合 存在しません 。
■ ８桁の場合 2個 見つかっています 。
63,317,664
→76,664,331−13,346,667 ＝63,317,664
97,508,421 →98,754,210−01,245,789 = 97,508,421
■ 全部で20個のカプレカ数が見つかっている・・・この先には？？
1桁のカプレカ数 0
3桁のカプレカ数 495
4桁のカプレカ数 6,174
6桁のカプレカ数 549,945 631,764
8桁のカプレカ数 63,317,664 97,508,421
9桁のカプレカ数 554,999,445 864,197,532
10桁のカプレカ数 6,333,176,664 9,753,086,421 9,975,084,201
11桁のカプレカ数 86,431,976,532
12桁のカプレカ数 555,499,994,445 633,331,766,664 975,330,866,421
997,530,864,201 999,750,842,001
13桁のカプレカ数 8,643,319,766,532
14桁のカプレカ数 63,333,317,666,664
15桁のカプレカ数 ???,???,???,???,???
・・・END・・・
97,508,421 →98,754,210−01,245,789 = 97,508,421
■ 全部で20個のカプレカ数が見つかっている・・・この先には？？
1桁のカプレカ数 0
3桁のカプレカ数 495
4桁のカプレカ数 6,174
6桁のカプレカ数 549,945 631,764
8桁のカプレカ数 63,317,664 97,508,421
9桁のカプレカ数 554,999,445 864,197,532
10桁のカプレカ数 6,333,176,664 9,753,086,421 9,975,084,201
11桁のカプレカ数 86,431,976,532
12桁のカプレカ数 555,499,994,445 633,331,766,664 975,330,866,421
997,530,864,201 999,750,842,001
13桁のカプレカ数 8,643,319,766,532
14桁のカプレカ数 63,333,317,666,664
15桁のカプレカ数 ???,???,???,???,???
・・・END・・・
お気に入りの記事を「いいね！」で応援しよう
[ＪＩＮさんの農園] カテゴリの最新記事
-
六つの村の睦み合い・藤沢市六会地区の歴… 2025.11.15
-
六つの村の睦み合い・藤沢市六会地区の歴… 2025.11.14
-
六つの村の睦み合い・藤沢市六会地区の歴… 2025.11.13
【毎日開催】
15記事にいいね！で1ポイント
© Rakuten Group, Inc.
