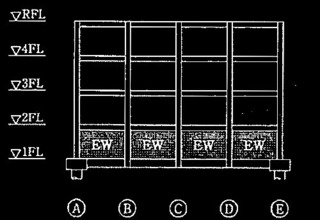
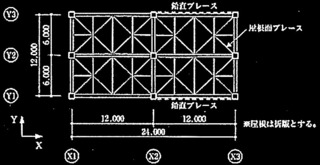
図1に示す2層の鉄骨ラーメン構造の建築物の崩壊メカニズムに関する以下の設問に解答せよ。なお、長期荷重による影響は無視するものとし、柱及び梁の部材断面、材種、基準強度F及び塑性断面係数Zpは、表1のとおりとする。
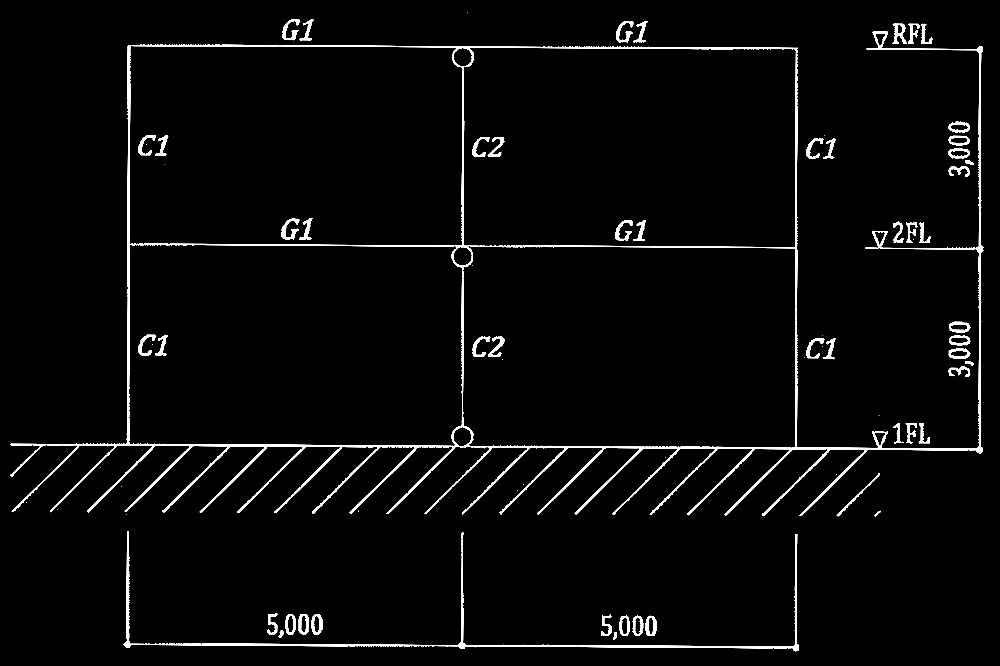
図1 骨組の解析モデル図(単位:mm、◯はピン接合を示す。)
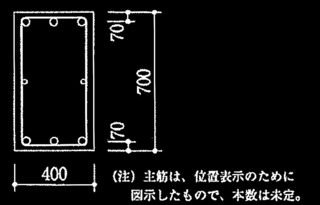
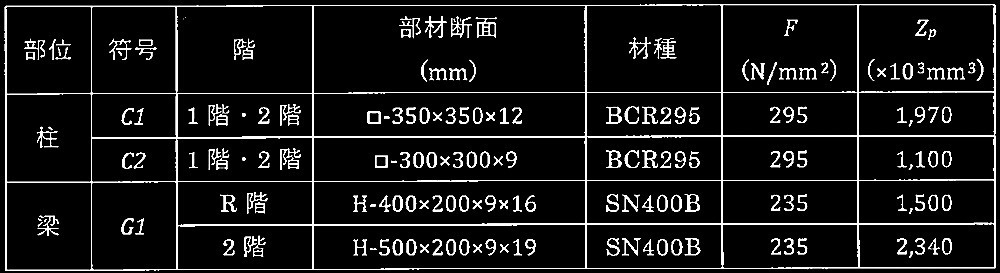
表1 柱及び梁の諸元
[ No.1 ]
表1に示した全ての柱及び梁の全塑性モーメントを算定せよ。なお、全塑性モーメント算定時の鋼材の降伏強度は基準強度Fの1.1倍とし、柱及び梁の全朔性モーメントは全断面有効と仮定し、柱の全塑性モーメントは軸力による低減はないものとする。解答は単位をkN・m とし、小数点以下を切上げて整数で示すこと。
答え
[ 解答解説 ]
・全塑性モーメントの算定
柱 1,2F
C1 c
M p
= c
F × c
Z p
= 295 × 1.1 × 1,970 × 10 3
/ 10 -6
= 640kN・m
柱 1,2F
C2 c
M p
= c
F × c
Z p
= 295 × 1.1 × 1,100 × 10 3
/ 10 -6
= 357 kN・m
梁 R
G1 b
M p
= b
F × b
Z p
= 235 × 1.1 × 1,560 × 10 3
/ 10 -6
= 404 kN・m
梁 2
G1 b
M p
= b
F × b
Z p
= 235 × 1.1 × 2,340× 10 3
/ 10 -6
= 605 kN・m
[ No.2 ]
図2は、左側から水平力が作用したときの、崩壊メカニズム形成時の曲げモーメント図である。答案用紙のフレーム図に、全ての塑性ヒンジの発生位置を●で示せ。
塑性ヒンジが柱と梁のどちらに発生するかは、接合部に取り付く柱の全塑性モーメントの和と、梁の全塑性モーメントの和との比較により判断すること。ただし、梁は保有耐力接合がなされており、パネルゾーン及び部材の中間部に塑性ヒンジは発生しないものとする。
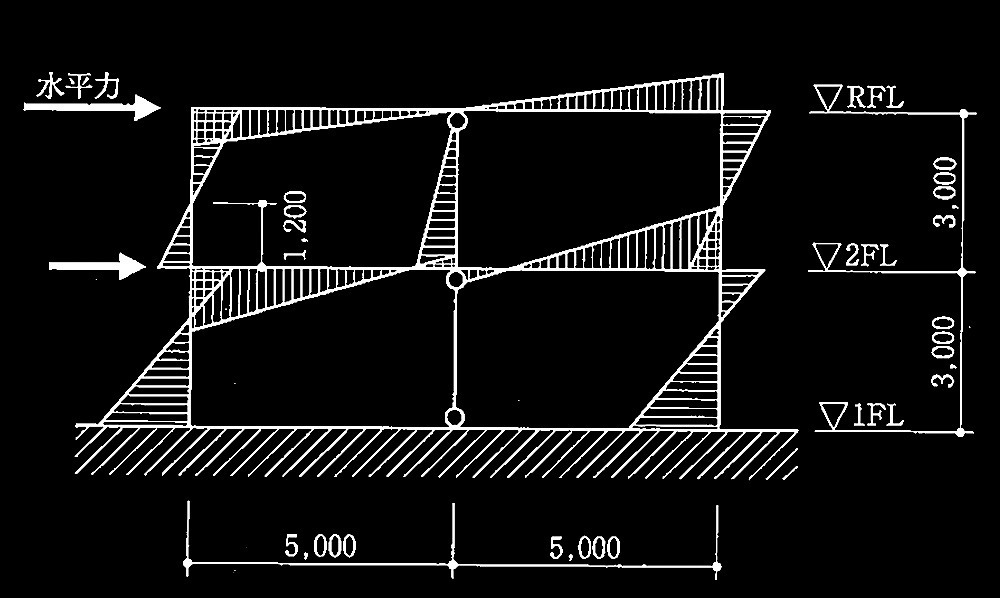
図2 崩壊メカニズム形成時の曲げモーメント図 (単位:mm)
答え
[ 解答解説 ]
・ヒンジの発生位置
RF 側柱 c
M p
( 2F
C1)
= 640 kN・m > b
M p
( RF
G1)
= 404 kN・m → 梁端部
2F 側柱 c
M p
( 2F
C1) + c
M p
( 1F
C1)
= 639 kN・m + 639 kN・m
=1278 kN・m > b
M p
( 2F
G1)
= 605 kN・m → 梁端部
2F 中柱 c
M p
( 2F
C2)
= 357 kN・m < 2 × b
M p
( 2F
G1)
= 605 kN・m × 2
= 1210 kN・m → 柱脚部
崩壊メカニズム形成のため、1階C1柱脚にもヒンジが発生する。また、崩壊メカニズムとしては全体崩壊型、部分崩壊型のどちらかが想定されるが、図2の1階柱頭の曲げモーメントが柱脚に比べて小さいため、全体崩壊型とした。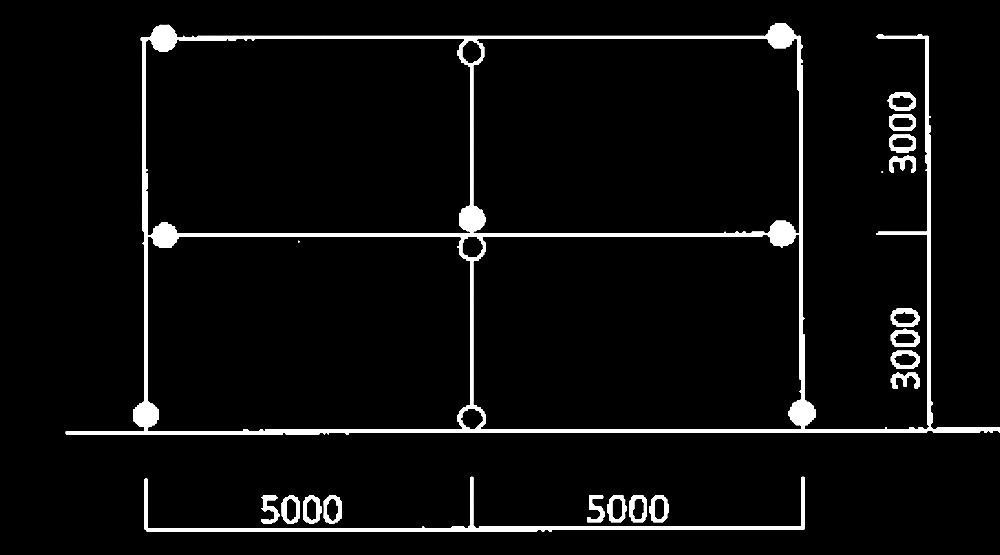
骨組のヒンジ発生位置を示す図(●がヒンジ発生位置)
[ No.3 ]
設問 [ No.2 ] の崩壊メカニズム形成時における右側の柱C1について、水平力によって生じる 2階の軸力 2F(C1-R) Nu、及び1階の軸力 1F(C1-R) Nuを求めよ。解答は圧縮を正、単位はkNとし、小数点以下を切上げて整数で示すこと。なお、塑性ヒンジの発生位置は節点位置としてよい。
答え
[ 解答解説 ]
問題[ No.1 ]で求めたヒンジ位置から軸力を算定する。
・2階軸力の算定
RFL梁端部にヒンジが発生することから、崩壊メカニズム形成時の柱付加軸力は下式となる。
2F(C1-R)
Nu = 2 × b
M p
( RF
G1)/梁スパン
=2 × 404kN・m/10m
= 81 kN
・1階軸力の算定
2階側柱は梁端部、中柱は2階柱脚にヒンジが発生することから、崩壊メカニズム形成時の柱付加軸力は下式となる。
1F(C1-L)
N E
= 2F(C1-R)
N u
+ ( b
M p
( 2F
G1) + c
M p
( 2F
C2) / 2) /梁スパン
= 81 kN+ (605 kN・m + 356 kN・m/ 2) / 5m
= 238 kN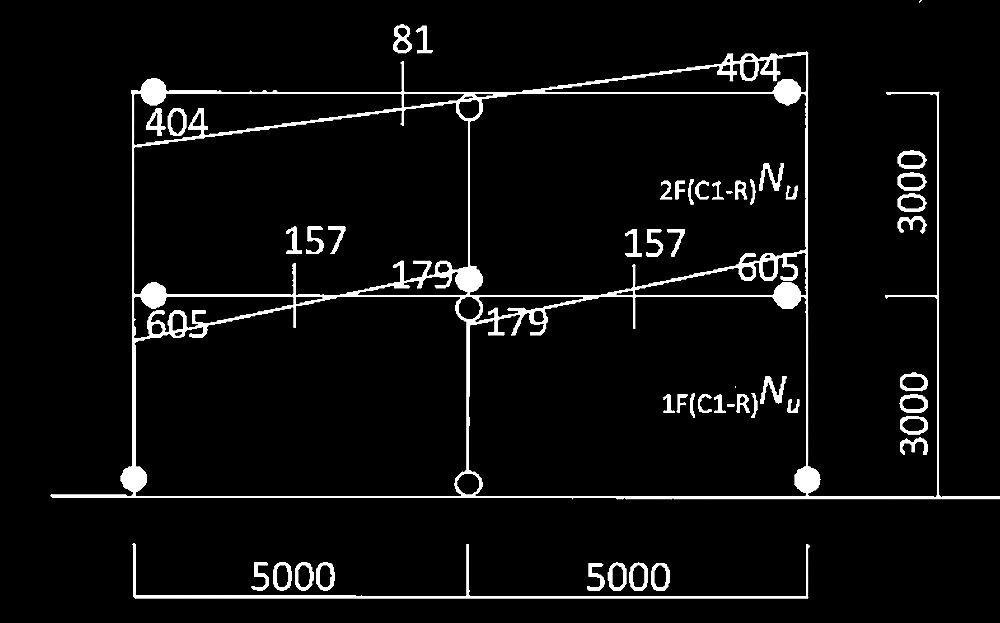
梁の曲げモーメント・せん断力図
[ No.4 ]
設問 [ No.2 ] の崩壊メカニズム形成時における2階の保有水平耐力 2F Q u 、及び1階の保有水平耐力 1F Q u を求めよ。解答は単位をkNとし、小数点以下を切上げて整数で示すこと。なお、 2階側柱の曲げモーメントの反曲点高さは、2FL+1,200mmとする。
答え
[ 解答解説 ]
問題 [ No.1 ]で求めたヒンジ位置から保有水平耐力を算定する。
・崩壊メカニズム時の曲げ応力及びせん断力分布は下図となる。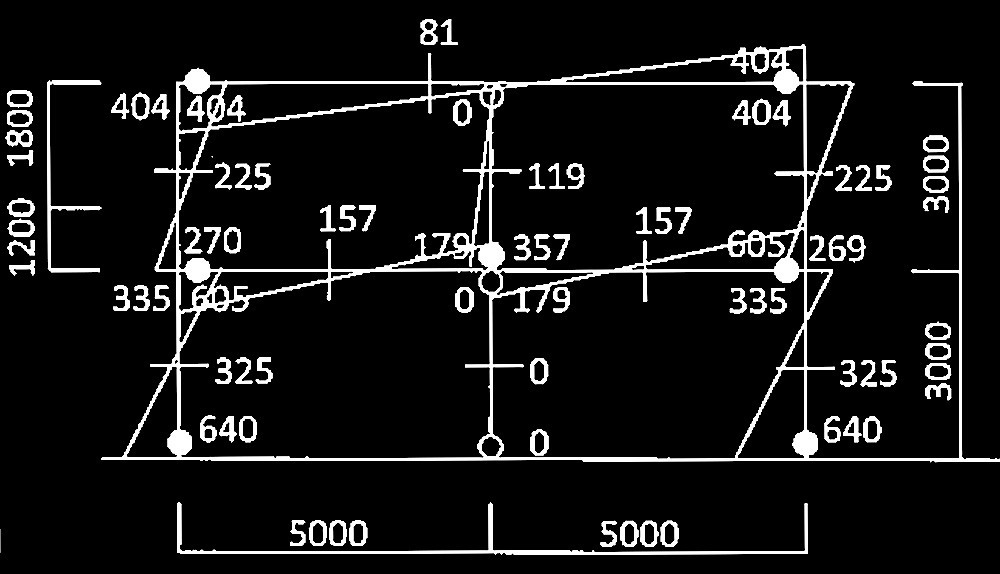
?@ 2階C1せん断力
404 kN /1.8m = 225kN
?A 2階C1柱脚曲げモーメント
225 kN × 1.2m =270 kN
?B 2階C2せん断力
375 kN /3.0m = 119 kN
?C 1階柱頭曲げモーメント
つり合い条件より
605 kN - 270 kN =335 kN
?D 1階C1せん断力
(335kN + 640kN)/3m = 325 kN
・保有水平耐力は下式となる。
2F
Q u
= 225 kN + 119 kN + 225 kN = 569 kN
1F
Q u
= 325 kN + 0 kN + 325 kN = 650 kN