2024年08月16日
令和二年度修了考査 構造設計(4肢択一式)No.1 〜 No.20
[ No.1 ]
建築物の耐震設計に関する次の記述のうち、最も不適当なものはどれか。
1. 事業継続計画(BCP)のために、地震時においても、建築物に財産保全と機能維持が要求される場合が増えている。
2. 建築基準法は、過去の地震災害等から得られた教訓及び最新の学術的知見によって改正されてきたことから、設計者はたとえ施行される前であっても、改正を先取りした構造設計を行うことが望ましい。
3. 地震を受ける構造物の挙動は動的なものであるが、動的解析は高度で繁雑であることから、耐震設計は動的効果を考慮した等価な静的荷重を用いる方法が認められている。
4. 鉄筋コンクリート造純ラーメン構造は、壁式構造とは異なり、柔軟で大きな塑性変形能力を有していることにより、中程度の地震動(稀に発生する地震動)に対して塑性変形を考慮した設計を行うことができる。
答え
4
[ 解答解説 ]
1.◯
記述のとおり。
2.◯
記述のとおり。
3.◯
記述のとおり。
4.×
中程度の地震動に対しては許容応力度設計が求められており、塑性変形は許容されていないため、誤り。
(テキスト第3章 2-2(1)稀に発生する地震動に対する許容応力度設計)
[ No. 2 ]
図A〜Dに示す鉄骨柱の座屈耐力Pの大小関係として、正しいものは、次のうちどれか。ただし、全ての柱は等質等断面であり、柱及び梁の重最は無視し、柱頭の面外方向の移動は拘束され、柱と梁は剛接されているものとする。また、ブレースは柱頭の水平移動を拘束し、ブレースの座屈は考えないものとする。
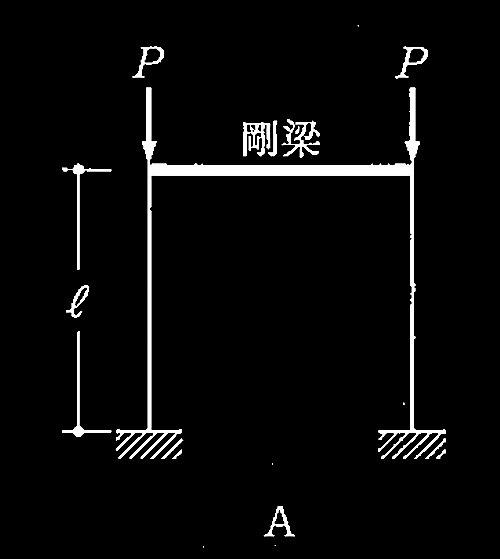
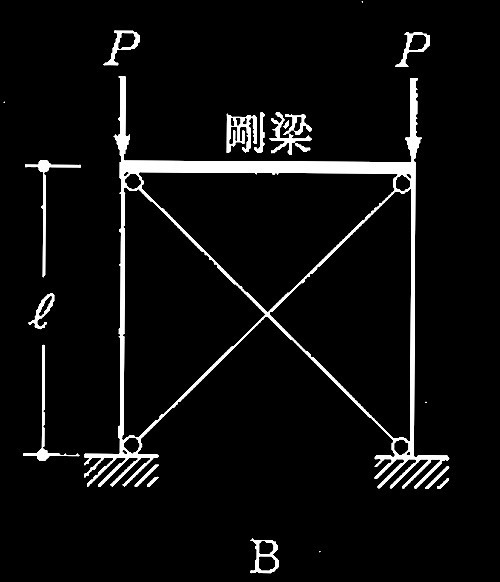
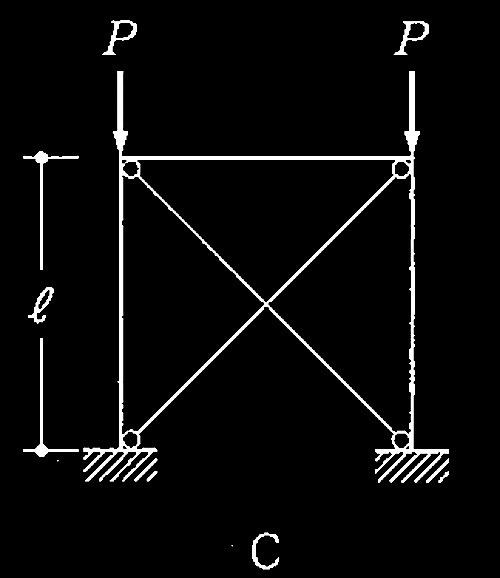
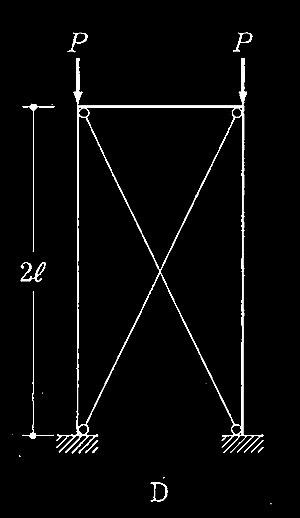
1. A = D < B = C
2. A < D < C < B
3. D < A < B < C
4. D < A < C < B
答え
4
[ 解答解説 ]
オイラーの座屈荷重は下式で示される。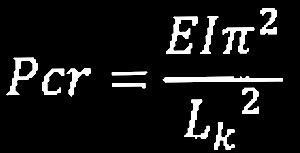
よって、座屈耐力Pは座屈長さLkの2乗に反比例する。
それぞれの架構の座屈長さは下記のとおりとなる。
A:下部固定端、上部固定端 、上部横拘束なし → Lk = 1.0?
B:下部固定端、上部固定端 、上部横拘束あり → Lk = 0.5?
C:下部固定端、上部ラーメン、上部横拘束あり
梁の長さや梁の断面についての記載がないため、
正確な座屈長さはわからない。
梁の剛性が無限に小さい場合は、
Lk = 0.7?から 0.5?< Lk < 0.7? となる
D:下部固定端、上部ラーメン、上部横拘束あり
Cと同様の拘束条件のため
0.5(2?) < Lk < 0.7 (2?) から
1.0?< Lk < 1.4?
以上より、各パターンの座屈長さ Lk は
B < C < A < D となるため、座屈耐力Pは
D < A < C < Bとなる。
[ No.3 ]
図のような2つの静定平面トラスがあり、トラス I はA点に、トラス ?U はB点に、それぞれ2Pの鉛直荷重を受けている。それぞれの載荷点の鉛直変位δAとδBの組合せとして、正しいものは、次のうちどれか。なお、全ての部材について断面積をA、ヤング係数をEとする。
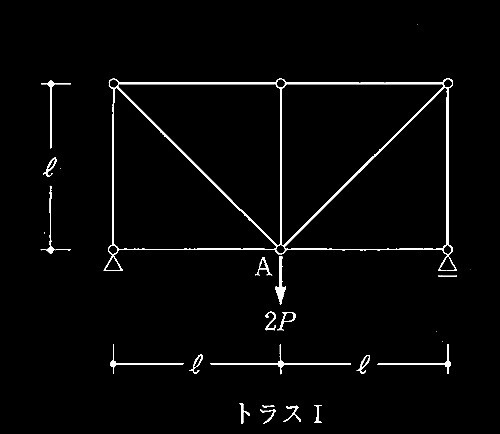
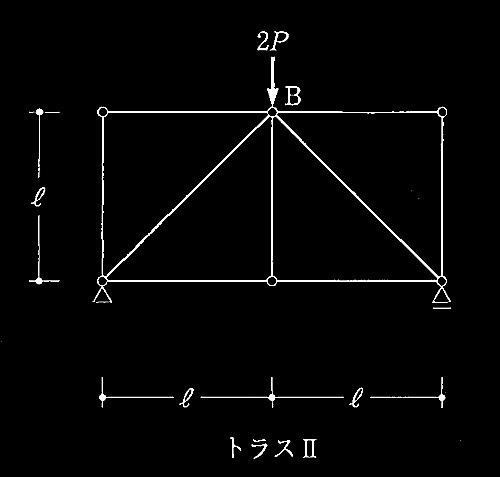

答え
3
[ 解答解説 ]
テキスト(第2章 1-3仮想仕事の原理とトラスの解析)にある仮想仕事の原理の単位仮想荷重法の式は次の通り。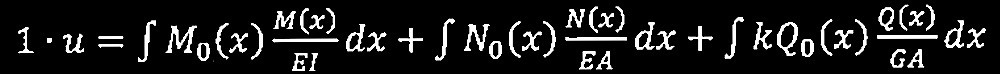
この問題はトラスのため、各材において曲げモーメント、せん断力の項は0であり、軸力は材軸にわたって一定である。よって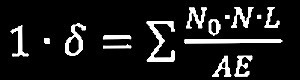
となる。
トラス I
トラスの軸力の解(引張を正とする)
実際の軸力N o
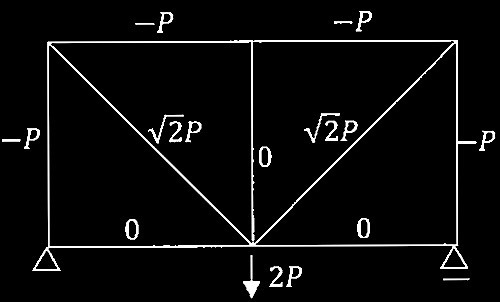
単位荷重による軸力N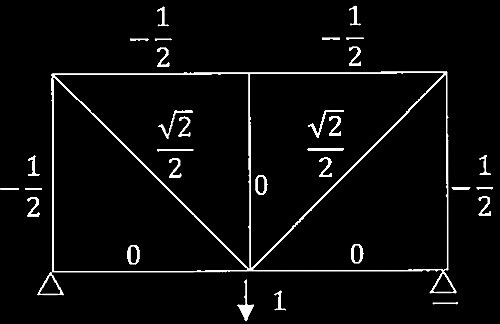
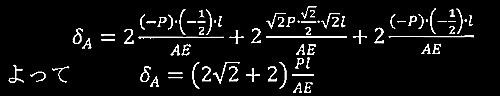
トラスII
トラスの軸力の解(引張を正とする)
実際の軸力N o
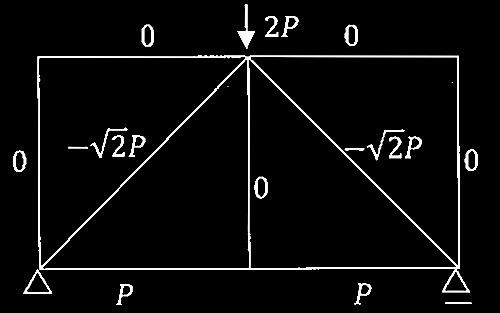
単位荷重による軸力N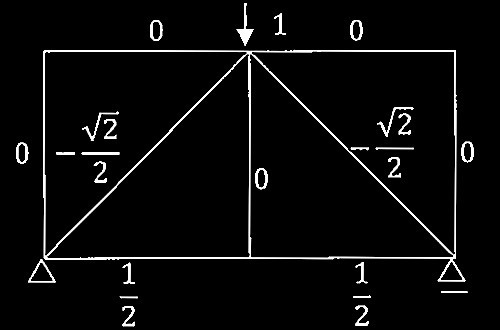
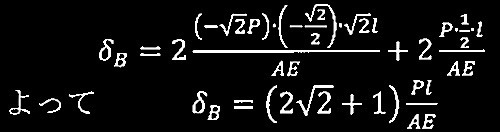
[ No.4 ]
構造材料に関する次の記述のうち、最も不適当なものはどれか。
1.コンクリートの圧縮強度時のひずみは、強度の高いコンクリートほど大きくなり、その値は、およそ0.015〜0.03%程度である。
2. 建築構造用鋼材の一軸載荷試験において、降伏点以上の応力度で正負交番繰返し荷重を作用させると、第1サイクル目の引張時には、弾性→降伏→降伏棚→ひずみ硬化という履歴特性が見られるが、それ以降の履歴には降伏棚は見られなくなる。
3. 耐火鋼は、SN材に耐熱性を高めるモリブデンなどの合金元素を添加して、高温域での耐火性能を高め、許容温度600℃(鋼材の長期許容応力度を600℃まで保持すること)を保証するように製造された鋼材である。
4. 木質構造においては、一般に、主要部材には含水率20%以下のものを使用するが、クリープ変形などを考慮して、含水率15%程度以下の材料を使用することが望ましい。
答え
1
[ 解答解説 ]
1.コンクリートの圧縮強度時のひずみはおよそ0.15%〜0.3%で、0.015%〜0.03%ではない。
(テキスト第2章 2-2(3)コンクリートの強度と材料定数)テキスト4章(テキスト第4章 3-1コンクリートの材料特性)では圧縮強度時のひずみは強度にも依存しないと記載されているが、2章に示されている実験結果からある程度強度が高いほど歪も大きくなっていると考えられる。
2. 記述の通り。
(テキスト第2章 2-1 (1)鋼材の機械的性質 )
3. 記述の通り。
(テキスト第2章 2-1(3)新しい建築構造用鋼材 )
4. 記述の通り。
(テキスト第2章 2-3(3)木材の含水率および耐久性」では、多くとも20%以下と記載している。「テキスト第4章 1-2(6)含水率」では、できるだけ乾燥材を使用しなければならないと記載している。また、含水率の表示で最も厳しいのが「D15」で15%以下であるから、記述は正しいと考えられる。)
[ No. 5 ]
建築物の構造計画に関する次の記述のうち、最も不適当なものはどれか。
1.地震力に対する抵抗メカニズムが強度型の構造は、鉄筋コンクリート造の耐震壁や鉄骨造のブレースなど、強度の大きい耐震要素を用いるものであり、塑性化の効果はほとんど期待していない。
2. 昭和46年建設省告示第109号に「高さ31mを超える建築物の屋外に面する帳壁は、1/100の層間変位に対して脱落しないこと」と規定されている。
3. 耐震要素の偏在により偏心が大きくなる場合には、直交方向のフレームの水平剛性を大きくし、地震時のねじり剛性を高めることで、偏心の影響を低減することができる。
4. 一般的な高層多スパンラーメン構造の場合、外柱の水平荷重時負担せん断力は、柱軸変形を考慮した場合のほうが考慮しない場合よりも小さくなる。
答え
2
[ 解答解説 ]
1.記述の通り。
(テキスト第3章 2-2(2)極めて稀に発生する地震動に対する保有水平耐力計算)
2. 1/150となっており、誤り。
(テキスト第2章 3-5(2)主に風荷重のみを受ける部材)
3. 記述の通り。
(テキスト第2章 3-4(2)水平荷重に対する計画)
4. 記述の通り。
(柱の軸方向変形を考慮した場合、梁に部材角が生じることにより梁部材端回転角が減少し曲げモーメントが小さくなる。)
[ No. 6 ]
建築物の構造解析に関する次の記述のうち、最も不適当なものはどれか。
1.耐震壁のモデル化において、耐震壁とその付帯柱を一体の柱とみなし、梁の部材に壁幅分の剛域を設ける「線材置換法」は、耐震壁が不規則に配置されている架構に対しても、精度よく解析できるモデル化である。
2. 建築物と地盤の力のやり取りを解析する場合、建築物の地下部分が深い場合などの特殊な条件での精算値を求めるには、地盤・建築物一体型解析モデルを用いる。
3. 一般に、動的解析における剛性比例型の減衰特性は、高次モードの影響が応答に表れにくいため、注意が必要である。
4. 等価せん断型の質点系振動モデルにおいては、ある層のせん断力は当該階のみの層間変形に依存し、他の層の変形の影響を受けないものと考え、質点をせん断バネで直列につないだ系としてモデル化している。
答え
1
[ 解答解説 ]
1.耐震壁が不規則に置換されるとき、剛域の考え方が難しく、精度が悪い(テキスト第2章 図4-2耐震壁のモデル化)、線材置換法は応力が小さい耐震壁に適用すべき(テキスト第4章 3-4部材のモデル化)とされており、誤り。
2. 記述の通り。
(テキスト第2章 4-2(3)動的解析c.建築物と地盤の相互作用)
3. 記述の通り。
(テキスト第3章 2-3(2)建築物の振動系モデル)
4. 記述の通り。
(テキスト第2章 4-2(3)動的解析)
[ No.7 ]
荷重・外力に関する次の記述のうち、最も不適当なものはどれか。
1.建築基準法は最低基準を規定しているという理由から、耐震規定には重要度係数や用途係数は規定されていない。
2. 通常、地震時に建築物が弾塑性挙動をすると仮定すると、建築物の最大応答加速度は入力地震動のおおむね3倍から5倍程度の値となる。
3. 昭和56(1981)年施行のいわゆる新耐震基準では、稀に発生する地震動に対する設計と、極めて稀に発生する地震動に対する設計の2段階の耐震設計が導入された。
4. 限界耐力計算の耐震計算における地震力は、まず建設地域の工学的基盤の標準地震動スペクトルを設定し、次に建設地点の表層地盤の増幅特性係数を用いて上部構造物の設計用応答スペクトルを設定して、算定する。
答え
2
[ 解答解説 ]
1.記述の通り。
(テキスト第3章 1-3(1)設計用荷重および外力に対する建築物の要求性能)
2. 建築物の最大応答加速度は、2.5倍〜3倍となるので、誤り。
(テキスト第3章 1-3(2)設計用荷重および外力の考え方)
3. いわゆる新耐震基準には、「稀に発生する地震動」や「極めて稀に発生する地震動」という言葉は書かれていないが、テキストにはそのように記載されているため、記述の通り。
(テキスト第3章 2-2(2)極めて稀に発生する地震動に対する保有水平耐力計算)
4. 記述の通り。
テキスト(第3章 1-3 (2)設計用荷重および外力の考え方)には限界耐力計算の地震力が工学的基盤のスペクトルで表現されていることが書かれている。設計では記述の通り、表層地盤の増幅特性係数を用いて設計用応答スペクトルを設定する。
[ No. 8 ]
耐震設計に関する次の記述のうち、最も不適当なものはどれか。
1.地震波にはいろいろな周期成分が含まれており、一般に、伝搬する過程において短周期成分は比較的早く減衰し、震源の遠い地震では相対的に長周期成分が多くなる。
2. 許容応力度設計では、終局時に構造物のどのような性能を保証しているかは明確ではない。
3. 限界耐力計算は構造物の地震動による応答が1次モードで近似できると仮定しているので、高さ方向に剛性あるいは質量分布が不均等となるような構造物には適用が難しい。
4. 時刻歴応答解析において内部粘性減衰に剛性比例型を用いると、高次モードの減衰は振動数に反比例して小さくなる。
答え
4
[ 解答解説 ]
1.記述の通り。
(テキスト第3章 2-1(1)地震と地震動)
2.記述の通り。
(テキスト第3章 2-2(1)稀に発生する地震動に対する許容応力度計算)
3.記述の通り。
(テキスト第3章 2-2(3)限界耐力計算)
4.×
剛性比例型の減衰では高次モードになる(振動数が大きいなる)ほど、減衰は大きくなるため。誤り。
(テキスト第3章 2-3(2)建築物の振動系モデル、テキスト第2章 4-2(3)動的解析)
[ No. 9 ]
耐風設計に関する次の記述のうち、最も不適当なものはどれか。
1.地表付近の風の性状は、建築物や樹木など地表面の粗さによって影響され、海岸付近や田園地帯など地表面が滑らかなほど、上層の風が地表付近でもそれほど弱まらず、乱れの少ない強風が吹く。
2. 平成12年建設省告示第1454号に定める基準風速Voは、平坦で開けた田園地帯などにおける高さ10mでの、再現期間50年の暴風の最大瞬間風速に相当する値である。
3. 風によって建築物に生じる振動については、通常の低層・中高層建築物では風方向振動を考慮すればよいが、超高層建築物ではそれに加えて、建築物の後流に発生する渦による風直交方向振動やねじれ振動の影響を考慮する必要がある。
4. 風によって生じる振動に対する居住性については法令上の規定はないが、建築物の用途によっては重要な課題であり、一般には、再現期間1年の風速による応答加速度により評価されることが多い。
答え
2
[ 解答解説 ]
1.記述の通り。
(テキスト第3章 3-3(2)地表面粗度区分の判定)
2. 基準風速V0は10分間平均風速に相当する値であり、誤り。
(テキスト第3章 3-3(2)地表面粗度区分の判定)
3.記述の通り。
(テキスト第3章 3-2(4)風により建築物等に生じる振動現象)
4.記述の通り。
(テキスト第3章 3-3(9)居住性の評価)
[ No. 10 ]
木質材料及び木質構造に関する次の記述のうち、最も不適当なものはどれか。
1. 木材は荷重継続の影響が大きいため、積雪荷重に対して「中長期」、「中短期」という概念を取り入れている。
2. 厚さ30mm前後の挽き板を1層ごとに繊維方向を直交させて積層接着したパネルを、CLT(Cross Laminated Timber)という。
3. 木造のいわゆる「四号建築物」の場合、構造計算を行えば、「壁量計算」を行う必要はない。
4. 1階が鉄筋コンクリート造で、2階及び3階が木造の混構造の場合、Aiを求める際の地震カ算定用重量の扱いが単一構造形式の場合と異なるので注意する必要がある。
答え
3
[ 解答解説 ]
1.記述の通り。
(テキスト第4章 1-2(7)荷重継続の影響)
2.記述の通り。
(テキスト第4章 1-4(8)集成材・合板・LVL・OSB等)
3.木造の場合、「壁量計算」は他の構造でいう「仕様規定」にあたるもので、構造計算を行った場合でも「壁量計算」を満足する必要があり、誤り。
(テキスト第4章 1.1(2)構造計算のルート)
4.記述の通り。
(テキスト第4章 1.1(3)構造のモデル化)
[ No. 11 ]
木質構造に関する次の記述のうち、最も不適当なものはどれか。
1.軸組構法の「耐力壁形式」の建築物では、一般に、柱と梁桁からなる軸組で鉛直荷重を支え、耐力壁が水平力を負担するものとしている。
2. 実験から耐力壁の許容せん断耐力を算定する際には、ばらつきを考慮して、複数の試験体を用いて実験を行い、それらの実験値の下限値を用いなければならない。
3. 性能表示制度の単位床面積当たりの必要壁率には、部分2階建てにおける地震力の違いが考慮されている。
4. 釘やボルト、ドリフトピンなどは、一般に、せん断に働くように用いる。
答え
2
[ 解答解説 ]
1.記述の通り。
(テキスト第4章 1-1(3)構造のモデル化)
2.実験の結果は3体の試験体の平均値にばらつき係数を乗じた値とするため、誤り。
(テキスト第4章 1-4(3)実験による壁の許容値の求め方)
3.記述の通り。
(テキスト第4章 1-7(6)性能表示の壁量計算)
4.記述の通り。
(テキスト第4章 1-5(6)「接合具」の強度評価)
[ No. 12 ]
鉄骨構造に関する次の記述のうち、最も不適当なものはどれか。
1. 鋼材は、温度が高くなると靱性が低下するので、鋼材の靱性を表す値として、シャルピー衝撃試験による0℃のときの吸収エネルギーが用いられる。
2. 鋼管柱の曲げ降伏耐力は、圧縮軸力の増大にともない低下する。
3. 根巻型柱脚では、鉄筋コンクリート部分で曲げモーメントを負担するので、塑性変形能力に優れたアンカーボルトを使用する必要はない。
4. 柱梁接合部の設計において、接合部パネルは幅厚比が大きくても塑性変形能力に優れていることが実験的に確認されていることから、柱の軸耐力に余裕がある場合、接合部パネル崩壊形を避けなくてもよい。
答え
1
[ 解答解説 ]
1.温度が低くなると靱性が低下するため、誤り。
(テキスト第4章 2-1(2)靱性)
2.記述の通り。
(テキスト第4章 2-2(3)曲げ圧縮材)
3.記述の通り。(誤りではないが、根巻き柱脚脚部の曲げ変形に応じてアンカーボルトにも大きな軸応力が生じ、かつせん断力を伝達する必要があるため、塑性変形能力が高いことが望ましい)
4.記述の通り。
(テキスト第4章 2-2(4)柱梁接合部パネル)
[ No. 13 ]
鉄骨構造に関する次の記述のうち、最も不適当なものはどれか。
1. 日本建築学会「鋼構造設計規準」では、鋼材の基準強度Fは、降伏点又は引張強さの70%のいずれか小さいほうの値を採用することが示されている。
2. 鋼材の応力ーひずみ関係において、一般に、温度が高くなると降伏点は低下し、ひずみ速度が速くなると降伏点が増大する特性を持つ。
3. 露出型柱脚を有する架構のモデル化では、アンカーボルトの配置に対応した回転剛性を評価したばねを柱脚部に設けるのが一般的である。
4. 限界細長比を超えた圧縮材の曲げ座屈耐力は、鋼材の降伏強度を大きくすることで増大させることができる。
答え
4
[ 解答解説 ]
1.記述の通り。
(テキスト第2章 2-1(2)鋼材の種類)
2.記述の通り。
(テキスト第4章 2-1(1)応力-ひずみ関係)
3.記述の通り。
4.圧縮材の曲げ座屈耐力は座屈長さと断面形状で決まる。よって鋼材の降伏強度を大きくしても座屈耐力は大きくならないため、誤り。
[ No.14 ]
図は、鉄筋コンクリート造2層多スパン均等平面骨組に水平力が作用したときの一部架構を切り出して示したものである。1階柱、2階柱梁接合部、及び2階柱にひび割れが発生する場合、ひび割れの方向を示す図として、最も適当なものは、次のうちどれか。

水平力を受ける鉄筋コンクリート造2層多スパン均等平面骨組
(一部架構を切り出して表示)




答え
3
[ 解答解説 ]
2階の柱は曲げ変形は主体となり、曲げモーメントの引張側にひび割れた発生する。1階柱は腰壁によりせん断変形が主体となり、変形する平行四辺形で延びる対角線の反対にひび割れが生じる。
柱梁接合部は左上-右下方向に引張られる(右上-左下方向に圧縮される)せん断変形となるので、右上-左下方向にせん断ひび割れが発生する。
[ No.15 ]
鉄筋コンクリート構造に関する次の記述のうち、最も不適当なものはどれか。
1.コンクリートのヤング係数は、圧縮強度が増大すると、ほぼ圧縮強度の平方根又は立方根に比例して増大するので、構造解析における部材剛性算定では、設計基準強度に対応したヤング係数を用いなければならない。
2. 鉄筋コンクリート造の柱では、鉛直荷重によってコンクリートに圧縮クリープが生じ、主筋の圧縮応力が徐々に増大していく。
3. 十分な量かつ適正な形状のせん断補強筋を用いれば、コア部分のコンクリートが拘束され、応カーひずみ関係が改善されることから、大地震時の1階柱脚断面での中立軸位置は、せん断補強筋量が少ない場合に比べて、断面中心に近くなる。
4. 付着割裂破壊の検討において、割裂面を横切る横補強筋櫨が多いほど付着割裂強度は上昇するが、横補強筋の降伏点を上げても付着割裂強度の上昇にはつながらない。
答え
3
[ 解答解説 ]
1. 記述の通り。
(テキスト第2章 2-2(3)コンクリートの強度と材料定数、
テキスト第4章 3-1コンクリートの材料特性)
2. 記述の通り。
(テキスト第4章 3-1コンクリートの材料特性、3-2鉄筋の材料特性)
3. コア部分のコンクリートが拘束された場合、ひずみが大きい領域での耐力低下が小さくなり、結果として中立軸の位置は断面中心から遠くなる。その結果、断面の応力中心間距離は大きくなり、より大きな抵抗モーメントが期待できる。よって誤り。
(テキスト4章3-8部材の変形性能)
4. 記述の通り。
[ No. 16 ]
免震構造・制振構造に関する次の記述のうち、最も不適当なものはどれか。
1. 免震構造の設計において、免震層に変形を集中させるためには、上部構造の層せん断剛性を大きくすることが効果的である。
2. 建築基準法上、制振建築物の設計は時刻歴応答解析(令第81条)によるほか、鋼材ダンパーに関しては、告示エネルギー法(平成17年国土交通省告示第631号)により行うことができる。
3. 制振建築物の設計において、主架構の応答加速度を低減するためには、できる限り多くのダンパーを用いることが効果的である。
4. 中高層の制振建築物の設計において、軸剛性及び軸耐力の高い制振部材を連層配置する場合、主架構の柱の軸剛性が十分に高くないと、制振部材周りの架構の曲げ変形成分が卓越し、層のせん断変形比率が下がり、ダンパーの効果が低下する。
答え
3
[ 解答解説 ]
1.記述の通り。
(テキスト第4章 6-1(1)免震構造の原理)
2. 記述の通り。
(テキスト第4章 6-2(3)制振部材による地震応答低減効果)
3. 入力する地震動にもよるが、設計用地震動のスペクトルが速度一定領域のあるスペクトルであるとすると、ダンパーを付加していくと、建物周期が短くなり、変位応答は小さくなるが、ある一定以上の剛性となると加速度低減効果が小さくなる特徴がある。そのため、ダンパー量が多すぎると加速度応答はかえって増加してしまうことがあるため、誤り。
(テキスト4章6-2(3)制振部材による地震応答低減効果)
4. 記述の通り。
(テキスト第4章 6-2(4)設計上の留意点)
[ No. 17 ]
地盤・基礎に関する次の記述のうち、最も不適当なものはどれか。
1. 標準貫入試験を実施すると対象地盤のN値が求められるが、同時にサンプラーにより採取した土を分析して、その土質と粒度分布などの物理特性を求めることができる。
2. 擁壁が背面の土に対して離れる方向に動くときに、擁壁に働く土圧は比較的小さな変位で極限釣合い状態(主働土圧状態)になる。
3. 直接基礎下に粘性土がある場合、建築物の自重によって圧密沈下が発生するかどうかの予測は、圧密試験を行い地盤自体の応力と建築物からの荷重による増加応力の合計が圧密降伏応力を超 えるかどうかで判断する。
4. 地震時に建築物からの水平力が杭に作用する場合に、杭体に発生する曲げモーメントの算定には、杭先端部付近の地盤の水平地盤反力係数の評価が重要である。
答え
4
[ 解答解説 ]
1. 記述の通り。
(テキスト第4章 7-3(2)地盤調査法)
2. 記述の通り。
(テキスト第4章 7-2(5)土圧・水圧)
3. 記述の通り。
(テキスト第4章 7-5(3)直接基礎)
4. テキスト(7-7)、(7-8)式にて算定する杭の曲げモーメントは杭頭部が大きく、杭頭部付近の水平地盤反力係数の影響が最も大きいため、誤り。
(テキスト第4章 7-5(4) d.杭の水平抵抗)
[ No. 18 ]
地盤・基礎に関する次の記述のうち、最も不適当なものはどれか。
1.地下水位より以深の飽和した緩い砂質土は、地震などの繰り返しせん断応力の作用により間隙水圧が上昇し、有効応力が消失すると、液状化現象が発生する。
2. 土のせん断強さを求めるときには粘着力と内部摩擦角を決めることが必要であり、砂質土の場合は粘着力が、粘性土の場合は内部摩擦角が支配的となる。
3. 直接基礎と杭基礎を併用した異種基礎を採用する場合には、異種基礎の境界部に発生することが想定される障害等を見極め、設計上の配慮を行う。
4. 杭の種類は、既製杭と場所打ちコンクリート杭に大別されるが、杭先端部付近を掘削時に杭径以上に拡大して、セメントミルクと土砂を撹拌混合する工法があるのは既製杭である。
答え
2
[ 解答解説 ]
1. 記述の通り。
(テキスト第4章 7-2(2)液状化)
2. 砂質土の場合は内部摩擦角、粘性土の場合は粘着力が支配的であり、誤り。
(テキスト第4章 7-2(4)せん断強さ)
3. 記述の通り。
(テキスト第4章 7-5(5)併用基礎)
4. 記述の通り。
[ No. 19 ]
建築物の非構造部材の設計に関する次の記述のうち、最も不適当なものはどれか。
1.外装材は建築物を構成する重要な要素であり、その耐風設計においては、構造骨組設計用と同じ風荷重を用いて、外装材の破損や飛散に対する安全性を検討する必要がある。
2. カーテンウォールの層間変位に対する追従性能を確保する方法としては、?@固定方式、?A 面内変形追従方式、?Bスウェイ方式(スライド方式)、?Cロッキング方式の4つの考え方があり、この中ではロッキング方式が最も高い層間変位追従性能を期待できる。
3. エキスパンションジョイントは中小地震時に構造体どうしが衝突しないクリアランス寸法を確保するとともに、当該ジョイント部が避難経路となる場合などでは大地震時においても可動部分の部品やカバー等が脱落しないように配慮する必要がある。
4. 特定天井とは、吊り天井であって、高さが6mを超える天井の部分で水平投影面積が200m 2 を超え、天井面構成部材等の単位面積質量が2kg/m 2 を超え、かつ、人が日常立ち入る場所に設置されているものをいう。
答え
1
[ 解答解説 ]
1.構造骨組み設計用の風荷重は平成12年建設省告示第1454号で算出するが、外装用は平成12年建設省告示第1458号によるため、誤り。
(テキスト第3章 3-3(5)構造骨組設計用と外装材等設計用の速度圧と風力係数)
2. 記述の通り。
(テキスト第4章 9-2変形追従型の耐震設計)
3. 記述の通り。
(テキスト第4章 9非構造部材)
4. 記述の通り。
[ No. 20 ]
既存建築物の耐震診断・耐震補強に関する次の記述のうち、最も不適当なものはどれか。
1. 1995年に阪神・淡路地域を襲った兵庫県南部地震では、1981年以前に設計 施工された建築物に甚大な被害が生じ、耐震補強の重要性が強く再認識された。
2. 鉄筋コンクリート造の耐震診断において第3次診断は、梁よりも先に、柱・壁などの鉛直部材が破壊する柱崩壊型建築物の耐震性能を簡略的に評価することを目的として開発された診断手法である。
3. 鋼構造では構造体の耐力が接合部耐力によって決定される場合が多く、その製作・施工状況により大きく影響を受けるため、鋼構造の耐震診断を精度よく行うためには構造体の接合部の現地調査が不可欠である。
4. 木造住宅の耐窟診断法における専門家向けの「一般診断法」は、耐震補強の必要性を判定することを主目的としており、診断は「地盤・基礎」と「上部構造」についてそれぞれ行うこととしている。
答え
2
[ 解答解説 ]
1.記述の通り。
(テキスト第5章 1-2既存建築物に対する耐震化対策)
2. 記述の内容は第2次診断についてもので、第3次診断は梁先行降伏が評価できる診断方法となっているため、誤り。
(テキスト第5章 2-2耐震性の判定)
3. 記述の通り。
(テキスト第5章 3鋼 耐震診断・耐震補強)
4. 記述の通り。
(テキスト第5章 4-2 一般診断法)
2024年08月14日
令和二年度修了考査 構造設計(記述式)問題1
問題1
図1は、鉄筋コンクリート造の耐力壁とスラブで構成され、スラブの重心位置で水平力2Qを受け、脚部が固定支持されている1層1スパンの架構モデルを表す。耐力壁は厚さ t、スラブは厚さ2tで、いずれも面外変形は拘束され、面内せん断力によるせん断変形のみが生じると仮定する。スラブと耐力壁の接合部は剛結されているものとする。
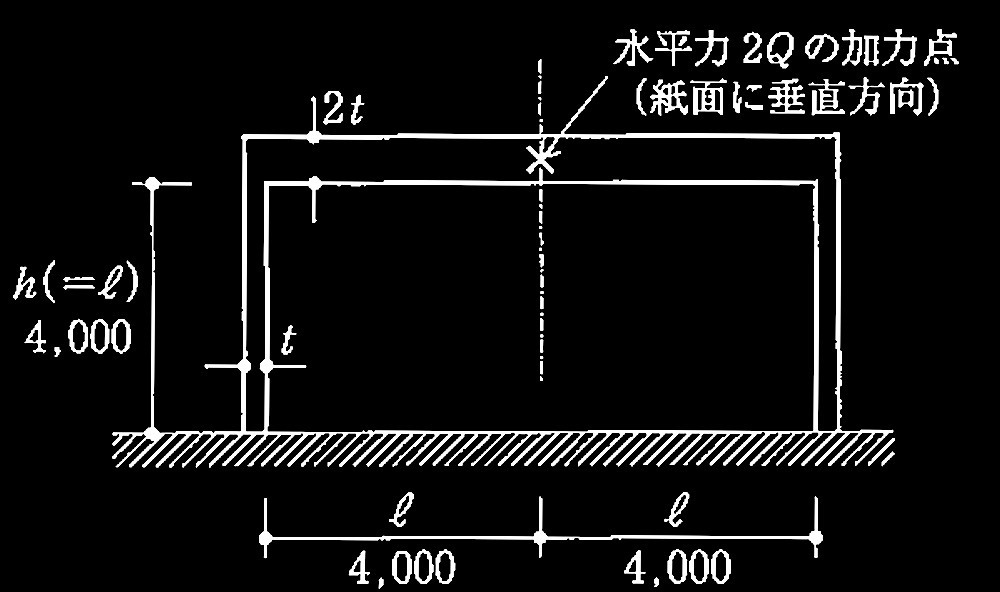
立面図(寸法単位mm)
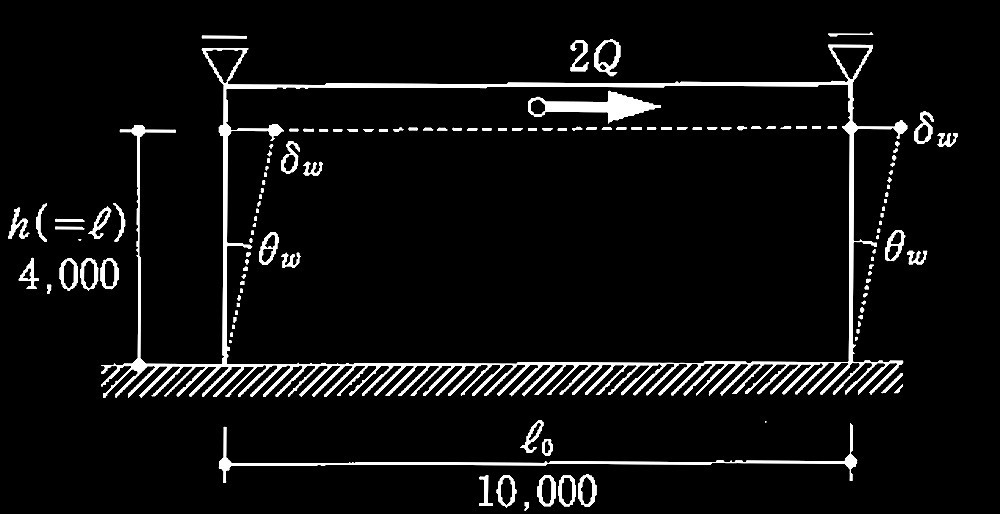
側面図及び耐力壁の変形図(寸法単位mm)
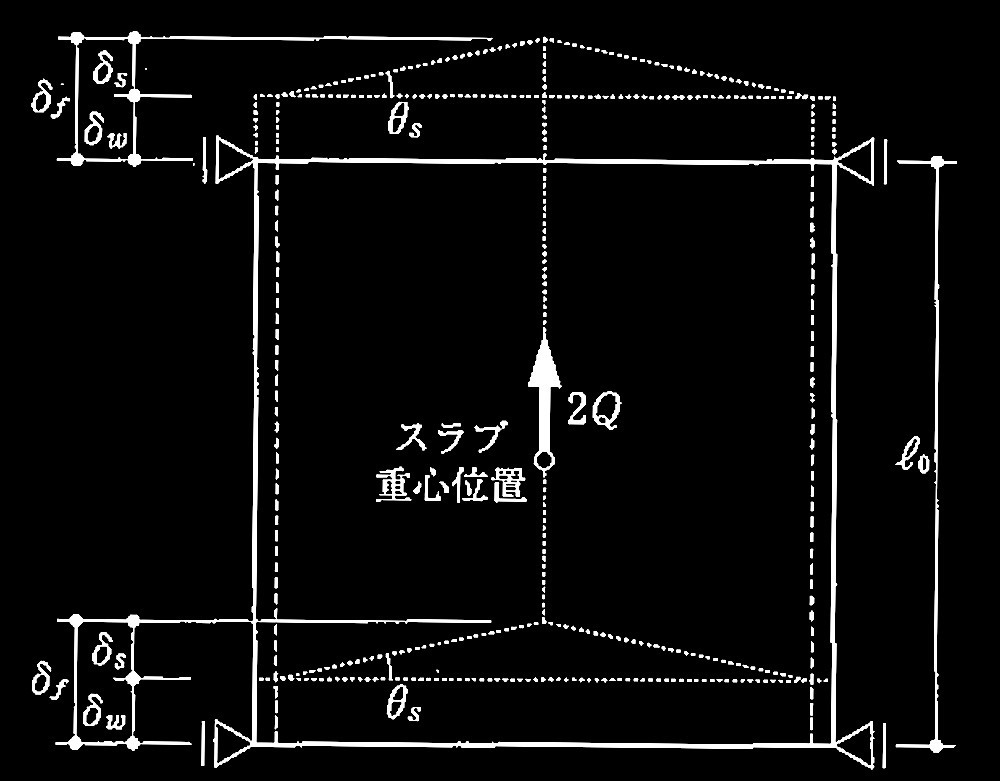
平面図及び加力点位置の変形図
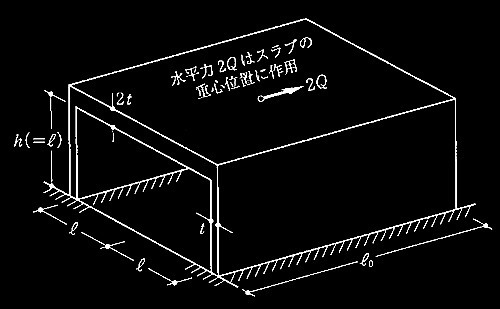
図1 架構モデル
スラブ及び耐力壁とも、十分なせん断補強筋が配置されており、面内せん断力によるせん断応力度τとせん断変形角θの関係は図2のようなバイリニア関係に理想化できるものとする。なお、スラブ及び耐力壁のせん断応力度τは、せん断力を断面積で除したものとする。
図2において第1折れ点は、せん断ひび割れが生じて剛性が低下することを示す。この時のせん断応力度τは 0.05Fc(コンクリートの短期許容せん断力相当、Fc はコンクリートの設計基準強度)とし、せん断変形角θは 0.25 × 10 -3 rad. とする。第2折れ点はせん断破壊が生じ、耐力を消失することを示す。この時のせん断応力度τは 0.20Fcとし、せん断変形角θは 4 × 10 -3 rad.とする。
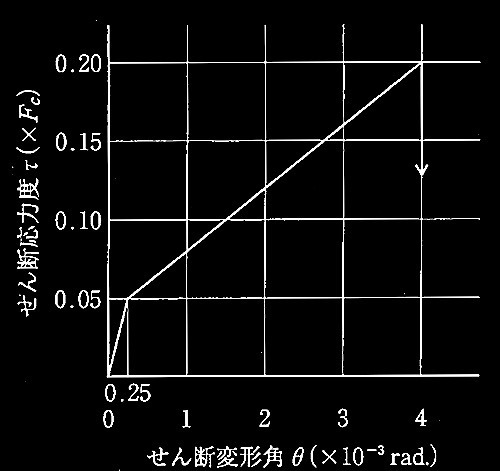
図2 スラブ及び耐力壁のせん断応力度τ-せん断変形角θ関係
この架構に関する以下の設問に解答せよ。
ただし、h = ?= 4,000mmとする。
[ No.1 ]
耐力壁がせん断破壊するときの、耐力壁のせん断変形量δ w 、スラブのせん断応力度τ s 、スラブのせん断変形量δ s 、及び架構の加力点位置の水平変位量δ f1 (= δ s + δ w )を求めよ。
答え
[ 解答解説 ]
・耐力壁がせん断破壊するときのせん断変形量δwは、そのときのせん断変形角をθwとすると、
δ w
=θ w
・h = 4 × 10 -3
× 4,000 = 16.0mm
・スラブのせん断応力度τ s
は、耐力壁のせん断応力度をτ w
(=0.20Fc)とすると、
τw = Q/( I o
・t) であることから、
τ s
= Q/( I o
・2t) = Q/( I o
・t)/2 =τ w
/2 = 0.20Fc/2 = 0.10Fc
・スラブのせん断変形量δ s
については、
スラブのせん断応力度τ s
= 0.10 Fcの時のせん断変形角θ s
は図2より
θ s
= 0.25 × 10 -3
+ (4.0 – 0.25) × 10 -3
/(0.20 – 0.05) × (0.10 – 0.05) =1.5 × 10 -3
rad.
従って、δ s
= θ s
・? =1.5 × 10 -3
× 4,000 = 6.0mm
・架構の加力点位置の水平変位量δ f1
、
δ f1
= δ s
+ δ w
= 6.0 + 16.0 = 22.0mm
[ No.2 ]
スラブの厚さを2tから半分のtに低減した場合について、耐力壁がせん断破壊するときの架構の加力点位置の水平変位量δ f2 を求めよ。また、この水平変位量は、設問 [ No.1 ]で求めた水平変位量δ f1 の何倍になるか、小数点以下2桁で示せ。
答え
[ 解答解説 ]
スラブ厚さが t のときのスラブのせん断応力度τ s2
は、耐力壁がせん断破壊するときのせん断応力度τ w
と等しくなり、
τ s2
= Q/( Io・t) = τ w
= 0.20Fc
そのときのスラブのせん断変形角θ s2
は
θ s2
= 4 × 10 -3
rad.
従って、δ f2
= δ s2
+ δ w
= θ s2
・?+ δ w
= 4 ×10 -3
× 4,000 +16.0=32.0mm
δ f2
/δ f1
= 32.0/22.0 ≒ 1.45
[ No.3 ]
耐力壁がせん断破壊するときでも、スラブのせん断変形を弾性範囲内(図2の第1折れ点以前)に収めるためには、スラブの厚さを耐力壁の厚さの何倍以上にすればよいか答えよ。
答え
[ 解答解説 ]
必要なスラブ厚さをn・tとすると、スラブのせん断応力度τ sn
は、
τ sn
= Q/(I o
・n ・t) = Q/(I o
・t)/n = τ w
/n
ここで、耐力壁がせん断破壊するときの τ w
= 0.20Fcで、
τ sn
≦ 0.05Fc となるためには、
τ sn
= 0.20Fc/n ≦ 0.05Fc
従って、 n ≧ 0.20Fc/0.05Fc = 4倍
となり、スラブの厚さを耐力壁の厚さの 4倍以上にすればよい。
[ No.4 ]
耐力壁を有する一般的な鉄筋コンクリート造建築物の設計を行うに当たり、耐力壁に確実にせん断力を伝達するために、スラブに生じる面内せん断応力度をどの程度に抑えればよいと思うか、その理由も含めて構造設計者としての考えを述べよ。
答え
[ 解答解説 ]
各荷重レベルに応じて、スラブに生じる面内せん断応力度のレベルを以下に記載するように抑えるべきと考える。
1) 土圧などの長期荷重時には、スラブに確実にせん断ひび割れを生じさせないために、コンクリートの長期許容せん断応力度以内とすべきである。
2) 短期荷重時(地震荷重時)、及び極めて稀に発生する風荷重時には、弾性剛性に基づいた応力解析によって層せん断力の配分を行なっていることから、スラブの剛性低下が生じないレベルとしてコンクリートの短期許容せん断応力度以内にすべきと考える。
3) 保有水平耐力時、又は極めて稀に発生する地震時には、スラブにせん断ひび割れが生じても大きな剛性低下が生じず、かつせん断破壊を生じさせないで剛床仮定を成立させなければならない。その為には、スラブのせん断応力度をFc/10程度以内に抑えるべきと考える。
近年では、スラブのせん断応力度を「鉄筋コンクリート造建物の靭性保証型耐震設計指針・同解説」による面内せん断ひび割れ応力度としての 0.33√ (σ B
)以内とする場合が多い。
2024年08月13日
令和二年度修了考査 構造設計(記述式)問題2
問題2
図に示すように水平力が作用する筋かい付き鉄骨架構に関する以下の設間に解答せよ。なお、筋かいは、断面積 A = 4,000mm 2 、弱軸回りの断面二次半径 i y = 40mmとし、引張、圧縮ともに働くものとする。鋼材はすべてSN400材(基準強度F=短期許容引張応力度σ y = 235N/mm 2 )である。また、柱は引張、圧縮いずれに対しても十分な耐力を有しているものとする。
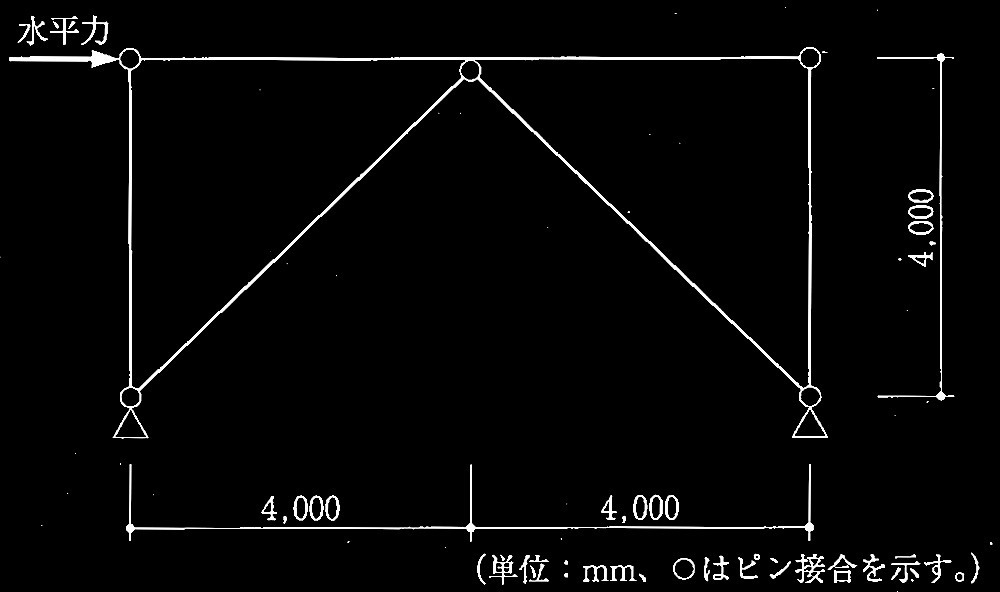
[ No.1 ]
本架構の引張筋かいの終局引張軸耐力を求めよ。なお、終局引張軸耐力は母材の短期許容引張軸力 N y ( = A・σ y ) とする。解答は単位をkNとし、小数点以下を切上げて整数で示すこと。
答え
[ 解答解説 ]
終局引張軸耐力は、
終局引張軸耐力 = N y
= A・σ y
= 4,000mm 2
× 235N/mm 2
= 940,000N → 940kN
となる。
(問題文に「終局引張軸耐力は母材の短期許容引張軸力 N y
(=A・σ y
)とする」および
「基準強度F=短期許容引張応力度 σ y
= 235N/mm 2
」
との記載があるため、材料強度用の1.1倍したF値は用いず、σ y
の値をそのまま用いた。)
[ No.2 ]
圧縮材の座屈時の材料強度 f c は式(1) で表される。本架構の圧縮筋かいについて、式(1) のf c に断面積Aを乗じた値を座屈時圧縮軸耐力 N c とする場合の N c を求めよ。解答は単位をkNとし、小数点以下を切上げて整数で示すこと。

答え
[ 解答解説 ]
圧縮筋かいの長さLは
L=√ (4,000mm 2
+ 4,000mm 2
) = 5,657mm
圧縮筋かいの両端部は面内並びに面外方向にも材軸直行方向の移動が拘束されたピン固定とすると、
細長比λは λ= L/i y
= 5,657mm/40mm = 141
となる。
限界細長比Λ は問題文の式より
Λ = 1,500/√(235N/mm 2
/1.5) =120
となる。
以上より
λ=141 > Λ=120であるため、
f c
は式(1)の下に示された式を用いて
f c
= { (3/5)/(141/120) 2
} × 235N/mm 2
×1.0= 102 N/mm 2
よって、座屈時圧縮軸耐力応 N c
は
N c
= 4,000mm 2
× 102 N/mm 2
= 408,000N → 408kN
となる。
(問題文に材料強度 f c
との記載があるが、
「基準強度F=短期許容引張応力度 σ y
= 235N/mm 2
」
とあることから材料強度用の1.1倍したF値は用いず、σ y
の値をそのまま用いた。通常は、材料強度の基準強度F値はJIS材であるため1.1倍とした値を用いている。)
[ No.3 ]
本架構の圧縮筋かいについて、終局圧縮軸耐力を座屈後安定耐力N u とする場合の終局圧縮軸耐力を求めよ。なお、筋かいの座屈後安定耐力は、式(2)で評価できるものとする。解答は単位をkNとし、小数点以下を切上げて整数で示すこと。
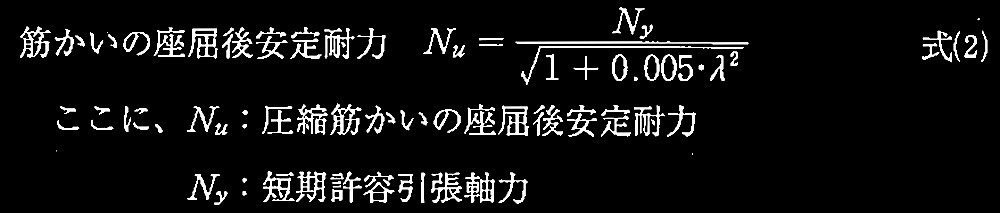
(日本建築学会:建築耐震設計における保有耐力と変形性能(1990)より)
答え
[ 解答解説 ]
筋かいの座屈後安定耐力
N u
= 940kN/√(1 + 0.005 × 141 2
) = 94KN
となる。
[ No.4 ]
水平力を増加させ、引張筋かいが終局引張軸耐力N y に達し、圧縮筋かいが座屈を生じた後、座屈後安定耐力N u となったときの梁の最大曲げモーメントM max を求めよ。また、そのときの曲げモーメント図を描け。ただし、梁は十分な曲げ耐力を有するものとする。曲げモーメン卜図は引張側に描き、M max は単位をkN・mとし、小数点以下を切上げて整数で示すこと。
答え
[ 解答解説 ]
筋かいに生じる軸力は、下図のようになる。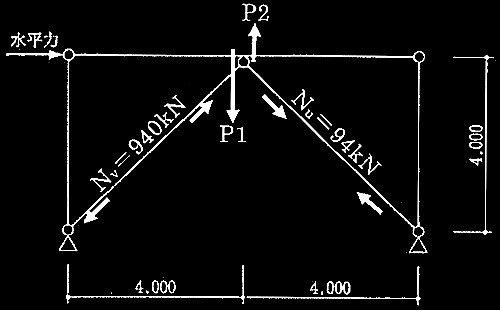
引張筋かいにより梁中央に生じる鉛直力P1ならびに、圧縮筋かいにより梁中央に生じる鉛直力P2はそれぞれ
P1 = 940kN × (4,000mm/5,657mm) = 665kN
P2 = 94kN × 同上=67kN
以上より、梁中央には軸力の変動により
P(下向き) = P1 − P2 = 665 − 67 = 598kN
の鉛直力が働く。
大梁は両端ピン支持の単純梁であるため、この鉛直力に応力は
両端部 Q = 598kN/2 = 299kN
梁の中央に生じる最大曲げモーメントは
M max
= 299kN × 4.0m = 1,196 kN・m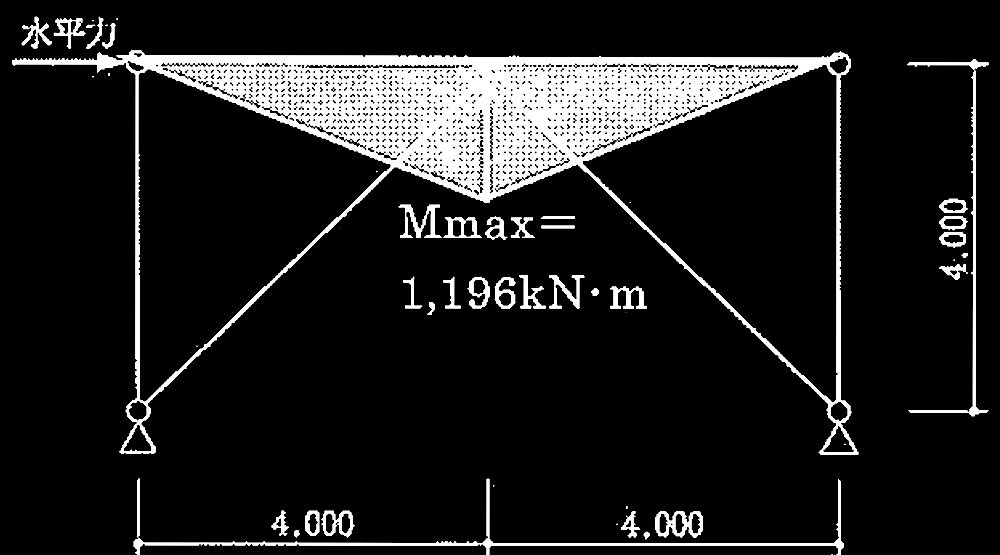
曲げモーメント図
[ No.5 ]
軸力による変動を考慮した梁の全塑性モーメントM p を1,000kN・mとしたときの崩壊メカニズム形成時の保有水平耐力P u を求めよ。なお、圧縮筋かいの軸力は座屈後安定耐力N u とする。解答は単位をkNとし、小数点以下を切上げて整数で示すこと。
答え
[ 解答解説 ]
梁の中央に生じる最大曲げモーメントM p
が 1,000kN・mとなる際に、梁中央に加わる鉛直力Pは
P = 1,000kN・m/4.0m × 2 = 500kN
圧縮筋かいの座屈後安定耐力N u
から梁中央に加わる鉛直力P2は全問のように
P2 = 67kNであるため
引張筋かいから梁中央に加わる鉛直力P1は
P1 = P + P2 = 500kN + 67kN = 567kN
となり、引張筋かいに生じている軸力は
N = 567kN × (5,657mm/ 4,000mm) = 802kN
となる。
崩壊メカニズム形成時の保有水平耐力 P u
は、引張・圧縮筋かいの負担軸力の水平成分の合計であるため
P u
= (802kN + 94kN) × (4,000mm/5,657mm) = 634kN
となる。
2024年08月12日
令和二年度修了考査 構造設計(記述式)問題3
同一敷地内に鉄筋コンクリート造地下1階、地上8階建ての事務所棟と、鉄骨造地上3階建ての付属棟を計画する場合の基礎の設計に関する以下の設問に解答せよ。当該敷地の地盤調査の結果から想定される地盤概要を図1に示す。
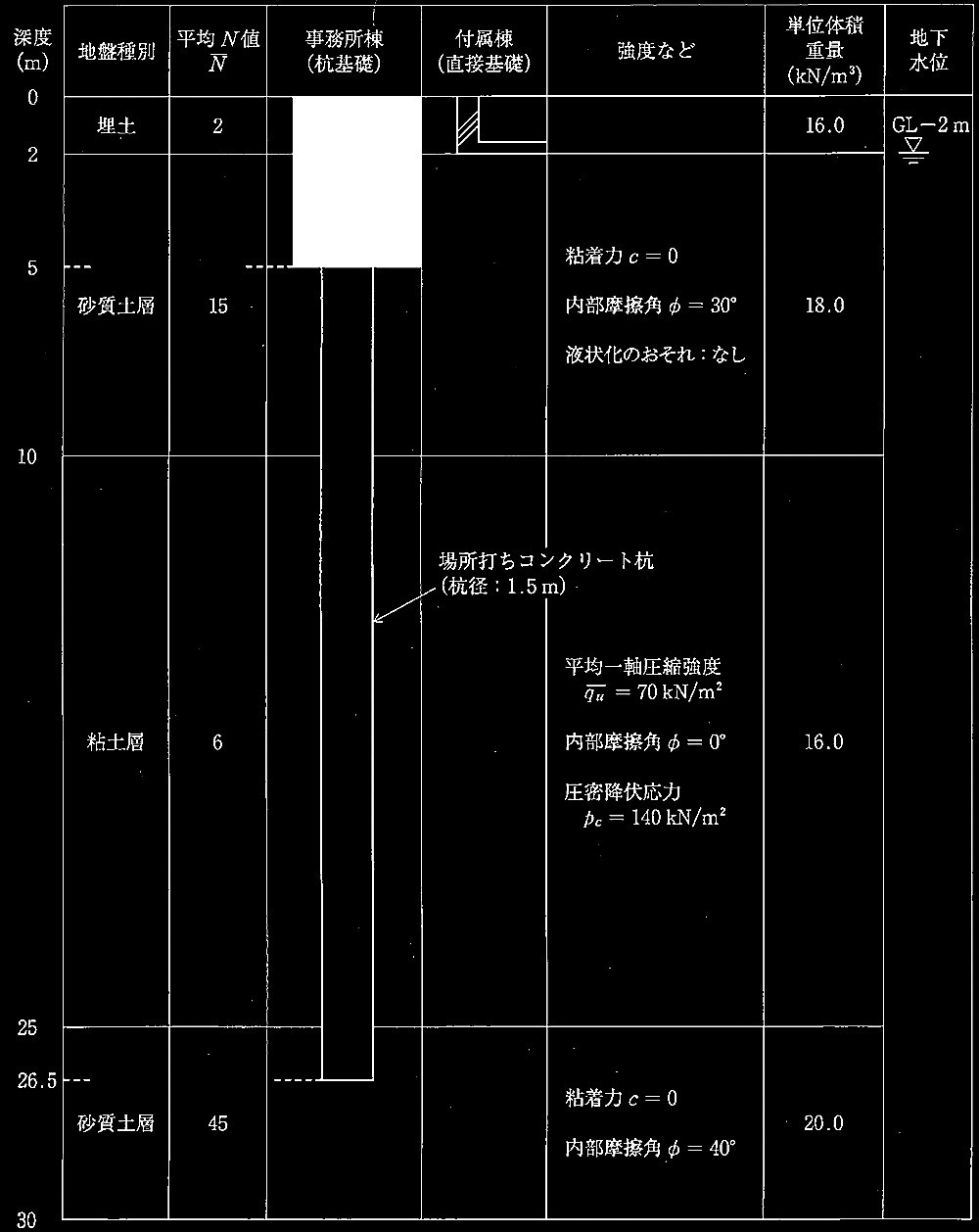
図1 地盤概要
[ No.1 ]
事務所棟の基礎形式は杭基礎を採用し、GL-25m以深に現れる砂質土層を支持層と想定して、以下のような杭の条件を設定した。次の?@〜?Bの設問に解答せよ。
<杭の種類> 場所打ちコンクリート杭(直杭)
<杭 径> 1.5m
<杭 長> 21.5m(杭先端深さGL-26.5m)
く基礎スラブ深さ> GL-5m
?@ 当該杭の1本当たりの極限先端支持力R p を式(1)より求めよ。

答え
[ 解答解説 ]
※数字の有効数字について、答えは3桁で表し、途中の計算も3桁で行った。最終桁の丸め方は四捨五入している。
?@ 平均N値:N =45
杭の先端支持力度 :q p
= 120・N
= 120・45 = 5400 (kN/m 2
)
杭 径:d = 1.5 (m)
杭先端の閉塞断面積:
A =πd 2
/4 = 3.142・1.5 2
/4 =1.77 (m 2
)
以上より、極限先端支持力R p
は式(1)より以下となる。
R p
= q p
・A= 5400・1.77 = 9558 → 9560(kN)
?A 当該杭の1本当たりの極限周面抵抗力Rfを式(2)より求めよ。ただし、杭先端の根入れ部分の周面抵抗力は無視するものとする。

答え
[ 解答解説 ]
砂質土部分の N値平均値:
N s
= 15
砂質土部分の周面抵抗力度:
τ s
= 3.3・N s
= 3.3・15 = 49.5 (kN/m 2
)
砂質土部分の長さ:
L s
= 5(m)
粘性土部分の周面抵抗力度:
τ c
= c u
= q u
/2 = 70/2 = 35.0 (kN/m 2
)
粘性土部分の長さ:
L c
= 15 (m)
杭の周長:
φ = π d = 3.142・1.5 = 4.71 (m)
砂質土部分の周面抵抗力:
R fs
=τ s
・ L s
・φ = 49.5・5・4.71 = 1170 (kN)
粘性土部分の周面抵抗力:
R fc
= τ c
・L c
・φ = 35・15・4.71 = 2470 (kN)
以上より、極限周面抵抗力R f
は式(2)より以下となる。
R f
= R fs
+ R fc
= 1170 + 2470 = 3640 (kN)
?B ?@及び?A で求めたRp及びRfを用いて、当該杭の1本当たりの長期許容鉛直支持力Raを求めよ。ただし、杭の自重は考慮しないものとする。
答え
[ 解答解説 ]
長期許容鉛直支持力R a
は極限先端支持力R p
及び極限周面抵抗力R f
より、以下となる。
R a
=( R p
+ R f
)/3 = (9560 + 3640)/3 = 4400 (kN)
[ No.2 ]
付属棟の基礎形式は直接基礎(べた基礎)を採用し、GL−2m以深に現れる砂質土層を支持層と想定して、以下のような条件を設定した。次の?@〜?Cの設問に解答せよ。
く基礎形式>
直接基礎(べた基礎:基礎底面 B × L=10m × 30m)
基礎の平均鉛直荷重度:40kN/m 2
く基礎荷重状況と地盤概要> 図2参照
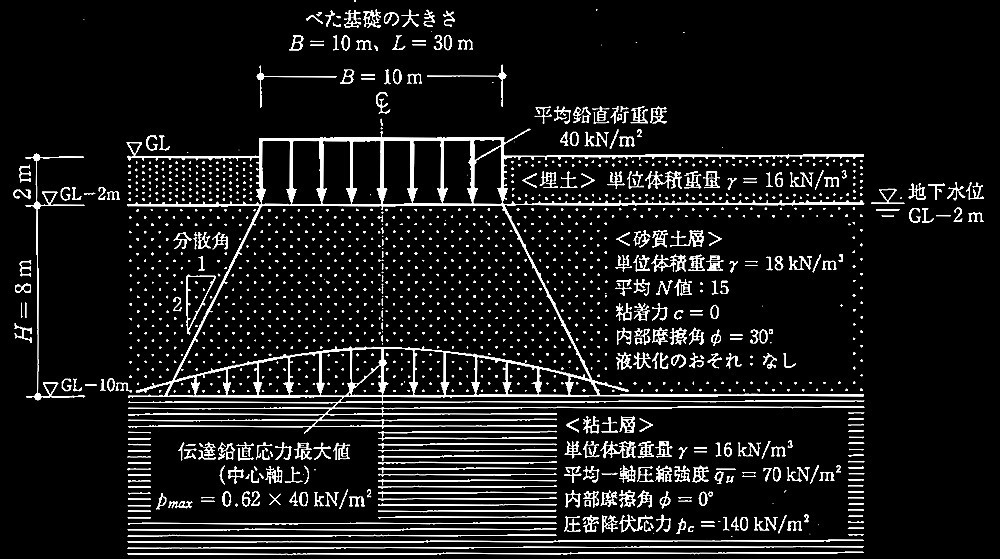
図2 基礎荷重状況と地盤概要
?@基礎直下の砂質土層の長期許容鉛直支持力度 q a1 を、式(3)を用いて求めよ。ただし、根入れ深さD f には埋土は考慮しないものとする。

表 支持力係数

答え
[ 解答解説 ]
※数字の有効数字について、答えは3桁で表し、途中の計算も3桁で行った。最終桁の丸め方は四捨五入している。
基礎の形状係数:
α= 1.0 + 0.2・B/L =1.0 + 0.2・10/30 = 1.07
基礎の形状係数:
β = 0.5 – 0.2・B/L = 0.5 - 0.2・10/30 = 0.433
支持力係数(φ = 30°):
N c
= 30.1、N γ
= 15.7、N q
= 18.4
支持地盤の粘着力:c = 0
支持地盤の単位体積董量:
γ 1
= 18 – 10 = 8 (kN/m 3
)
(地下水位以下のため水中単位体積重量)
根入れ部分の士の単位体積重量 :
γ 2
= 16 (kN/m 3
)
根入れ深さ:
D f
= 0 (m) (埋土は考慮しないため)
以上より、基礎直下の砂質土層の長期許容鉛直支持力度q α1
は式(3)より以下となる。
q α1
=(α・c・N c
+ β・γ 1
・B・N y
+ γ 2
・D f
・N q
)/3
= (1.07・0・30.1 + 0.433・8・10・15.7 + 16・0・18.4)/3
= 181 (kN/m 2
)
?A 直接基礎底面(GL-2m)に作用する鉛直荷重が、分散角1/2で粘土層表面(GL-10m)に(B + H)・( L + H )の大きさに均等に載荷されるものとして、直接基礎底面(GL-2m)に換算した粘土層の長期許容鉛直支持力度q α2 を、式(4)を用いて求めよ。ただし、根入れ深さD f は砂質土層厚Hとし、埋土は根入れ深さに考慮しないものとする。

答え
[ 解答解説 ]
基礎の形状係数:
α= 1.0 + 0.2・(B + H)/(L + H)
= 1.0 + 0.2・(10+ 8)/(30+ 8)
= 1.10
基礎の形状係数:
β= 0.5 – 0.2・(B + H)/(L + H)
= 0.5 – 0.2・(10+ 8)/(30+ 8)
= 0.405
支持力係数(φ =0°):
N c
= 5.1、N γ
= 0.0、N q
= 1.0
支持地盤の粘着力:
c =q u
/2 = 70/2 = 35 (kN/m 2
)
支持地盤の単位体積重量:
γ 1
= 16 – 10 = 6 (kN/m 3
)
(地下水位以下のため水中単位体積重量)
根入れ部分の土の単位体積重量:
γ 2
= 18 –10 = 8 (kN/m 3
)
(地下水位以下のため水中単位体積重量)
根入れ深さ:D f
= H = 8 (m)
以上より、直接基礎底面(GL-2m)に換算した粘土層の長期許容支持力度q α2
は式(4)より以下となる。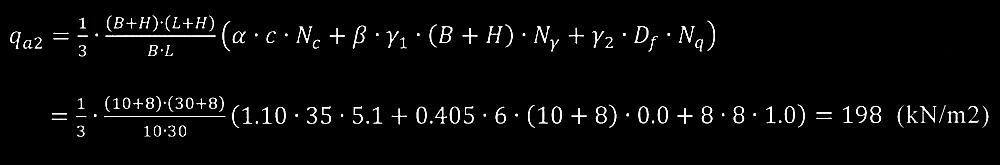
く参考>
通常、基礎底から存在している砂質土層下の2層地盤としての粘土層の許容支持力から砂質土層の重量を引く必要があり学会基礎指針2019に準拠して算出する。粘土層の長期許容支持力度q’ α2
は式(3)より以下となる。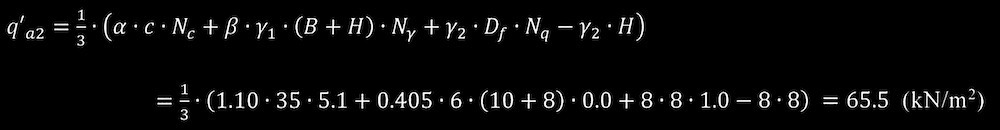
粘土層の長期許容支持力度q'a2から直接基礎底面(GL-2m)に換算した粘土層の長期許容支持力度q a2
は以下となる。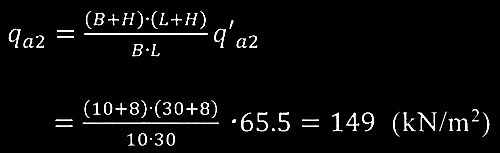
?B 圧密沈下が発生するか否かを計算により判定せよ。ただし、基礎の鉛直荷重度による粘土層の上面(GL-10m)の中心軸上の伝達鉛直応力の最大値P max は、図2に示すように 0.62 × 40 kN/m 2 とする。圧密沈下の検討では埋土の重量も考慮するものとする。
答え
[ 解答解説 ]
埋土の重量:
wb =γ・2 =16・2 = 32.0 (kN/m 2
)
砂質土層の重量:
w s
= (γ − 10) ・H = (18 − 10)・8 = 64.0 (kN/m 2
)
伝達鉛直応力の最大値:
P max
= 0.62 × (40 − 32) = 4.96 (kN/m 2
)
粘土層にかかる最大荷重:
P d
= w b
+ w s
+ p max
= 32.0 + 64.0 + 4.96 = 101 (kN/m 2
)
くPc= 140 (kN/m 2
)
以上より、粘土層にかかる最大荷重pdは101kN/m 2
であり、粘士層の圧密降伏応力度
p c
= 140kN/m 2
未満であるため、圧密沈下は発生しない。
?C 以上の?@〜?Bの検討より、本付属棟を図2に示すような直接基礎(べた基礎)で設計することが可能か否かを判断せよ。あわせて、その理由を述べよ。
答え
[ 解答解説 ]
基礎直下の砂質土層の長期許容鉛直支持力度q α1
は181kN/m 2
、直接基礎底面(GL-2m)に換算した粘土層の長期許容支持力度q α2
は198kN/m 2
であり、直接基礎底面の長期許容鉛直支持力度q α
は両者を比較して小さい方を採用し、181kN/m 2
となる。基礎の平均鉛直荷重度は40kN/m 2
であり、長期許容鉛直支持力度以下である。?Bの検討により、圧密沈下も発生しない。以上より、基礎の構造安全性に問題はなく、本付属棟を直接基礎(べた基礎)で設計することが可能である。

