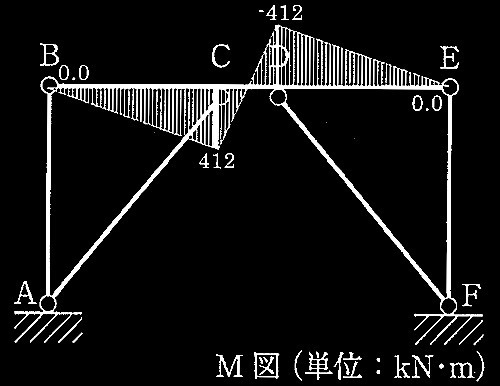
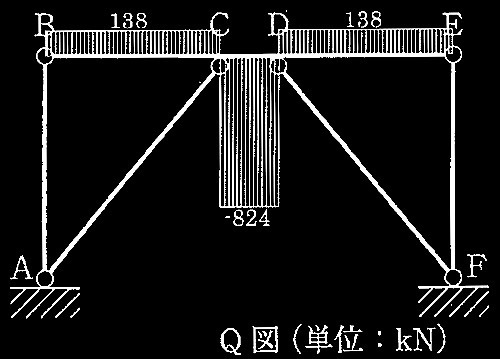
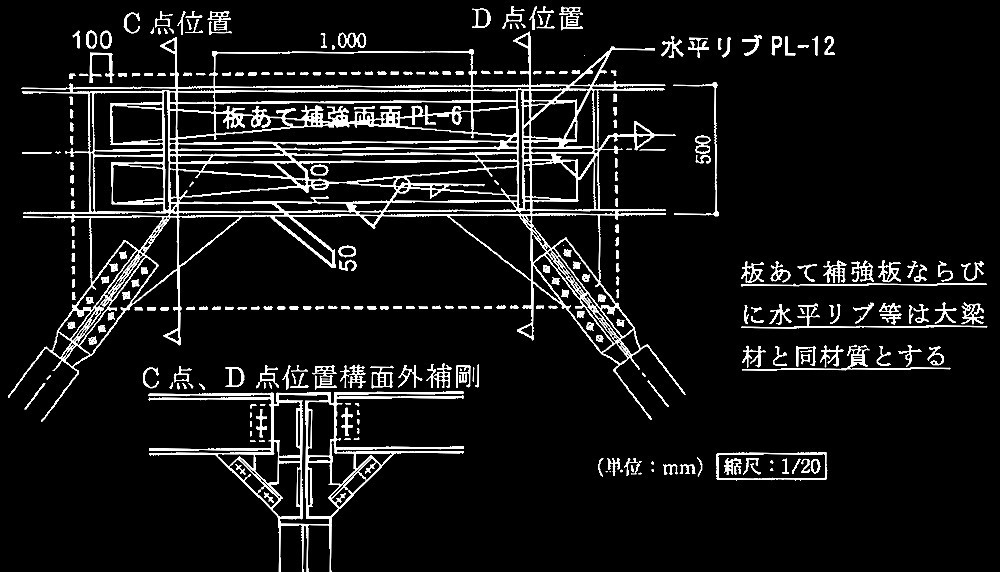
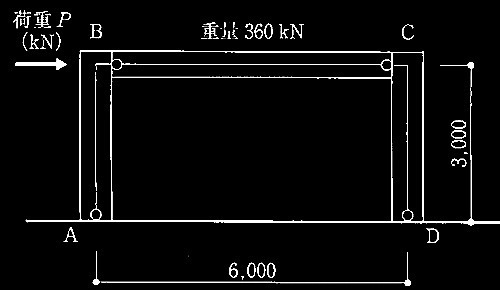
(選択理由記述式4肢択ー問題)
[ No.1 ]
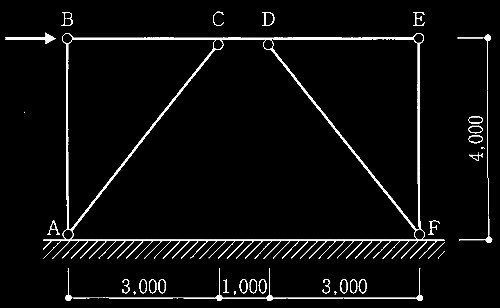
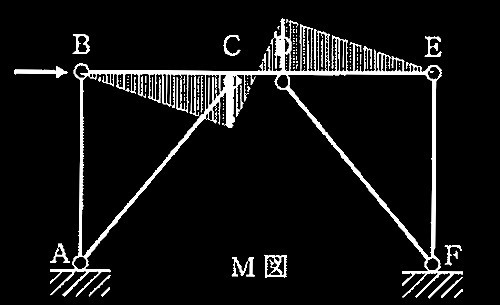
図のようなスパンL、高さHが同じであり、柱脚の固定条件が異なる2つの骨組A、骨組Bがある。骨組A、骨組Bとも、梁は剛体、柱は完全弾塑性体からなり、全ての柱は同断面、同材料からなる。次の記述のうち、 誤っているものを1つ選び、 誤りとする理由を述べよ。
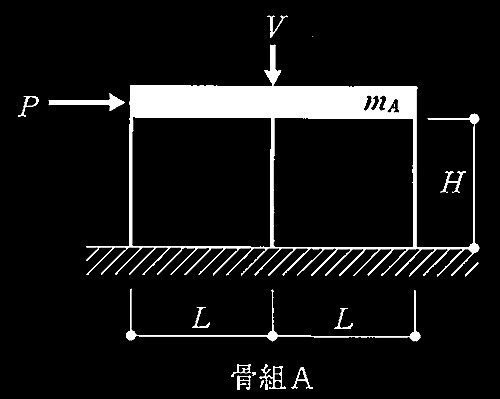
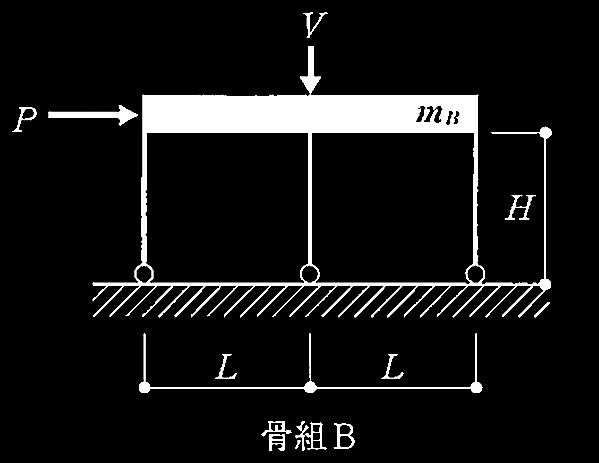
1. 水平荷重Pを受ける場合、骨組Aの水平剛性K A 、骨組Bの水平剛性K B の比は、K A : K B =4: 1である。
2. 水平荷重Pを漸増させていくと、塑性崩壊に至る。軸力の影響を考慮しなければ、骨組Aの塑性崩壊荷重P A 、骨組Bの塑性崩壊荷重P B の比は、P A :P B =2: 1である。
3. 骨組Aと骨組Bの固有周期が同じ場合、骨組Aの質量m A 、骨組Bの質量m B の比は、m A : m B = 2: 1である。
4. 水平荷重Pは作用しないものとし、鉛直荷重Vを漸増させていくと座屈が発生する。骨組Aの弾性座屈荷重V A 、骨組Bの弾性座屈荷重V B の比は、V A :V B = 4 : 1 である。
答え
3
[ 解答解説 ]
1.記述の通り。
変形から剛性を求める。
柱1本あたりの荷重はP/3となり、片持ち梁のたわみの公式から骨組Bの変形は
δ B
= H 3
/3EI × (P/3)
両端固定の場合は長さが1/2の場合の片持ち梁の2倍と同じになるので、
骨組Aの変形は
δ A
= 2(H/2) 3
/3EI × (P/3)
水平剛性 K = P/δより
K A
= 36EI/H 3
、K B
= 9EI/H 3
よって、K A
:K B
=4 : 1
2.記述の通り。
塑性破壊が曲げ降伏による崩壊形であるかは記述されていないが、せん断破壊しないものとして検討を行う。
柱の塑性モーメントをM u
とすると、骨組Aは柱上下端がM U
となり、骨組Bは上端のみM u
となる。この時の柱1本あたりのせん断力は骨組Aでは Q A
=2Mo/H 骨組BではQ B
=Mo/H となるので、P A
:P B
= 3 × Q A
:3 × Q B
= 2:1
3.固有周期の公式は T = 2π√(m/k)。 1.より水平剛性の比は4: 1のため、周期が同じとなるためには質量比もm A
:m B
= 4:1である必要がある。
よって、不適当。
4.記述の通り。
オイラーの座屈荷重は
P cr
= π 2
EI/L k
2
ここで、L k
は座屈長さ
両端固定で水平拘束なしの場合、
L k
= H よって P crA
= π 2
EI/H 2
片側ピンで水平拘束なしの場合、
L k
= 2H よって P crB
= π 2
EI/(2H) 2
よって、V A
: V B
= P crA
: P crB
= 4 : 1
[ No. 2 ]
構造材料に関する次の記述のうち、 最も不適当なものを選び、 不適当とする理由を述べよ。
1. 鋼材の引張試験から得られた応カーひずみ関係は、通常の設計で使用するような塑性ひずみの小さな範囲では圧縮側でも成立するとして、座屈を考慮しない範囲で同じ値が適用される。
2. ステンレス鋼の機械的性質の特徴は、明瞭な降伏点を示さないラウンドハウス形の応カーひずみ関係をもつこと、降伏比が高いことである。
3. コンクリートの応カ-ひずみ関係は、設計基準強度によってヤング係数が変わり、圧縮強度が高いほど剛性も高い。
4. 木材の含水率が繊維飽和点(おおむね30%)以下では、含水率の低下に伴ってその強度は増加する。
答え
2
[ 解答解説 ]
1.記述の通り。
(テキスト第Il 編第1章2-1鋼材P. 123)
2.降伏比は低いので、不適当。
SUS304 約0.4 < SS400 約0.6
(テキスト第Il 編第1章2-2鋼材 P. 126)
3.記述の通り。
(テキスト第Il編第1章2-2鉄筋コンクリート P. 131)
4.記述の通り。
(テキスト第Il編第1章2-3木材 P. 134)
[ No. 3 ]
構造計画・構造解析に関する次の記述のうち、 最も不適当なものを選び、 不適当とする理由を述べよ。
1. 同断面積で鋼管厚が同厚のCFT柱では、角形鋼管より円形鋼管のほうが、充填コンクリートのコンファインド効果が大きく、曲げ剛性も大きい。
2. L形の平面形をした建築物の構造計画において、基礎免震構造を採用し、免震層の剛心を上部構造の重心位置と一致させることにより、偏心の影響を小さくすることができる。
3. 大きな吹抜けのある鉄骨造建築物の耐震設計を行うに当たり、構造解析においてスラブの面内変形を考慮し、柱•梁•スラブなどの部材設計を行った。
4. 鉄筋コンクリート造建築物において、偏心を小さくするために耐力壁にスリットを設ける場合があるが、偏心が多少大き<なっても耐力壁の量を確保したほうが耐震性能として優れている場合もある。
答え
1
[ 解答解説 ]
1.コンファインド効果の説明は正しいが、曲げ剛性は向きによっては角型鋼管の方が大きくなるので不適当。
2.記述の通り。
3.記述の通り。
4.記述の通り。
[ No. 4 ]
耐震設計に関する次の記述のうち、 最も不適当なものを選び、 不適当とする理由を述べよ。
1. 建築物の地震力を求める場合、一次設計の標準せん断力係数Coは0.2以上としなければならないが、地盤が著しく軟弱な区域として特定行政庁が規則で指定する区域内の木造建築物(除外規定あり)にあっては0.3以上とする必要がある。
2. 地盤の液状化現象は、一般に、均ーで緩い砂質地盤において地下水位が浅い場合に、地震の揺れによって間隙水圧が低下し土粒子間のせん断抵抗を失うことによって生じる。
3. 保有水平耐力計算において、構造物が水平力を受けて崩壊形が形成されるときの層せん断力を、保有水平耐力とする。
4. 時刻歴応答解析による耐震設計において、地震動に与える表層地盤の影響は、工学的基盤より上部の地盤による入力地震動の増幅を評価することで考慮される。
答え
2
[ 解答解説 ]
1.記述の通り。
(施行令第88条第2項)
2.液状化は間隙水圧の上昇によって有効応力が減少することで発生するため、誤り。
(テキスト第II編第3章7-2地盤に関する基礎知識P. 333)
3.記述の通り。
(テキスト第II編第2章2-2耐震設計法P. 177)
4.記述の通り。
(テキスト第1I編第2章2-3時刻歴応答解析による耐震設計P. 185)
[ No. 5 ]
鉄骨構造に関する次の記述のうち、 最も不適当なものを選び、 不適当とする理由を述べよ。
1.鋼材の降伏比が小さいほど、塑性ひずみが部材の長さ方向に広がるため、粘りのある部材となる。
2. 冷間成形角形鋼管の柱に筋かい材のガセットプレートを取り付ける場合には、筋かいの力による鋼管板要素の面外変形などの局部的な変形を防止する必要がある。
3. 細長比が弾性限界細長比以下の圧縮材が繰返し軸力を受け曲げ座屈すると、座屈後の軸耐力が低下し、ある一定値に漸近するような荷重ー変形挙動を示す。
4. 同じスパンの単純梁において、均等曲げを受ける場合と逆対称曲げを受ける場合では、均等曲げを受ける場合のほうが、横座屈曲げ耐力が大きくなる。
答え
4
[ 解答解説 ]
1.記述の通り。
(テキスト第II編第1章2-1鋼材P. 123)
2.記述の通り。
3.記述の通り。
(テキスト第II編第3章2-2部材の設計P. 255)
4.モーメント勾配がある場合は、等曲げの場合に比べて横座屈耐力は大きくなるので、均等曲げを受ける場合の方が、横座屈曲げ耐力は小さくなる。
よって誤り。 (テキスト第II 編第3章2-1鋼材の特性P. 256)
[ No. 6 ]
鉄筋コンクリート造の構造設計に関する次の記述のうち、 最も不適当なものを選び、 不適当とする理由を述べよ。
1. 柱梁接合部の鉄筋折曲げ定着部において、折曲げ内法直径が小さいほど折曲げ部分の内側に発生する支圧力が大きくなるので、コンクリートの局部圧縮破壊を避けるために、鉄筋の折曲げ内法直径の最小値が規定されている。
2. コンクリートの乾燥収縮は、水セメント比が同じであれば、セメント量の多い調合のものほど大きくなる。
3. 必要保有水平耐力の算定に当たり、コンクリートの設計基準強度 Fcに対する崩壊メカニズム時の柱の平均せん断応力度τuの比が大きくFC部材になったので、せん断補強筋を増やして FA部材とした。
4. 1階をピロティとした計画において、2階の耐力壁の下枠梁に、1階柱の主筋が十分に定着できる梁せいを確保し、耐力壁の下枠梁の主筋は、2階耐力壁の水平せん断力の1/2 程度を負担できる量を確保した。
答え
3
[ 解答解説 ]
1.記述の通り。
2.記述の通り。
3.柱の部材種別の決定のうちせん断に関するものは、τu/Fc の数値であり、せん断補強筋を増やしても部材種別は変更できないため、不適当。(昭 55建告第1792号第4)
4.記述の通り。
[ No. 7 ]
木質構造等の構造設計に関する次の記述のうち、 最も不適当なものを選ひ、 不適当とする理由を述べよ。
1. スキップフロアを有する木造建築物においては、スキップ境界面に接して直交方向に面材張り耐力壁等を設けるのが望ましい。
2. 1階が鉄筋コンクリート造で2階及び3階が木造の建築物において、1階を耐力壁の多い構造としておけば、木造階の剛性率が0.6以下の場合であっても、剛性率による割増し(Fs)は必要ない。
3. 耐力壁を主たる水平耐力要素とする木造建築物では、一般に、水平力に対する各層の荷重変形性能は独立とみなせる。
4. 曲げ応力を受ける横架材の引張側に欠込みがある場合、欠込み部分の曲げの検定では、欠込み部分を除いた断面に対する断面係数を用いた。
答え
2
[ 解答解説 ]
1.記述の通り。
2.混構造の場合、木造階の剛性率は0. 6以上を満足する必要があるため、不適当。
(テキスト第1I編第3章1-1木質構造建築物の概要P. 224)
3.記述の通り。
4.記述の通り。
[ No. 8 ]
免震構造•制振構造に関する次の記述のうち、 最も不適当なものを選び、 不適当とする理由を述べよ。
1. 制振ダンパーの接合部は、変形能力を確保するために、剛性を小さく設計することが望ましい。
2. 免震建築物における免震層の固有周期は長くすることによって応答加速度を小さくできるが、上部構造の固有周期は長くするより短くし、免震層に振動エネルギーを集中させることが望ましい。
3. 免震構造では、免震層を含む建築物の固有周期が長くなるため、免震層上部の応答加速度は減少するが、地面に対する応答変位は増大する。
4. 制振建築物の計画において、長周期地震動や台風などの多数の繰返し振動によって制振ダンパーの性能が低下する場合があるので、その性能低下を考慮に入れた構造設計を行う必要がある。
答え
1
[ 解答解説 ]
1.制振ダンパーの接合部は、ダンパー軸剛性•軸耐力に対して十分な剛性を有している必要があり、不適当。
(テキスト第 ?U 編第3章6-2制振構造P. 329)
2.記述の通り。
(テキスト第 ?U 編第3章6-1免震構造P. 319)
3.記述の通り。
(テキスト第 ?U 編第3章6-1免震構造P. 319)
4.記述の通り。
[ No. 9 ]
地盤•基礎に関する次の記述のうち、 最も不適当なものを選び、 不適当とする理由を述べよ。
1.地震動を受ける地盤では、地盤のせん断ひずみの増大とともに、せん断剛性Gは低下し、減衰定数hは増大する。
2. 地盤中から採取した粘性土の室内力学試験を行う際に、試料採取深さが比較的深い場合には、三軸圧縮試験(UU試験)より一軸圧縮試験のほうが有効である。
3. 原位置で固化材(主にセメント)と地盤を攪拌混合する地盤改良では、地盤及びセメントの特性によっては、改良体から六価クロムの溶出の可能性があるので、事前に溶出試験を行うことが重要である。
4. 杭の鉛直方向の抵抗要素として先端抵抗と周面摩擦抵抗があり、杭頭部に鉛直力が作用したときに、沈下の発生とともに周面摩擦抵抗が先行して発揮され、沈下が増加すると先端抵抗が発揮される。
答え
2
[ 解答解説 ]
1.記述の通り。
2.サンプリング深さが深い場合には、サンプリングから試験時までに応力開放などで資料にひび割れなどが発生することがあるため、3軸圧縮試験を行うのが望ましいため、不適当。
(テキスト第 ?U 編第3章7-2地盤に関する基礎知識P. 334)
3.記述の通り。
(テキスト第 ?U 編第3章7-4基礎構造計画P. 340)
4.記述の通り。
(テキスト第 ?U 編第3章7-5基礎の設計P. 347)
[ N'o. 10 ]
建築物の耐震診断•耐震補強に関する次の記述のうち、 最も不適当なものを選び、 不適当とする理由を述べよ。
1. 鋼構造建築物の耐震診断において、床面の面内剛性が小さく、地震時にその形状保持が難しいと判断される場合は、必要に応じて平面骨組に分け、骨組の形状、荷重の伝達と各部の挙動を考慮した検討が必要である。
2. 「既存鉄筋コンクリート造建築物の耐震診断基準•同解説」において、第1次から第3次までの3種の診断レベルが用意されており、第2次診断は、柱、壁に加えて梁の耐力を考慮して耐震性能を評価するなど、第1次診断より計算精度の改善を図っている。
3. 鋼構造建築物の耐震補強において、補強設計時には、耐震診断時の実態調査結果の確認を行うとともに、ボルト接合部や溶接接合部については必要に応じて追加確認をすることが重要である。
4. 鉄筋コンクリート造建築物の耐震補強において、既存柱に対する鋼板の巻き付けによる補強は、極脆性柱や下階壁抜け柱のせん断耐力改善に効果が期待できる工法である。
答え
2
[ 解答解説 ]
1.記述の通り。
(テキスト第II編第4章3-2耐震性の判定P. 387)
2.第2次診断で想定しているのは柱崩壊型の構造特性で、梁は剛強と考え計算では考慮しないため、不適当。
(テキスト第II編第4章2-2耐震性の判定P. 381)
3.記述の通り。
(テキスト第II編第4章3-2耐震性の判定P. 387)
4.記述の通り。