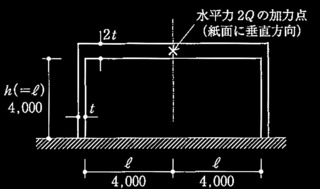
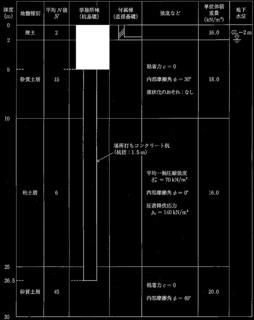
問題2
図に示すように水平力が作用する筋かい付き鉄骨架構に関する以下の設間に解答せよ。なお、筋かいは、断面積 A = 4,000mm 2 、弱軸回りの断面二次半径 i y = 40mmとし、引張、圧縮ともに働くものとする。鋼材はすべてSN400材(基準強度F=短期許容引張応力度σ y = 235N/mm 2 )である。また、柱は引張、圧縮いずれに対しても十分な耐力を有しているものとする。
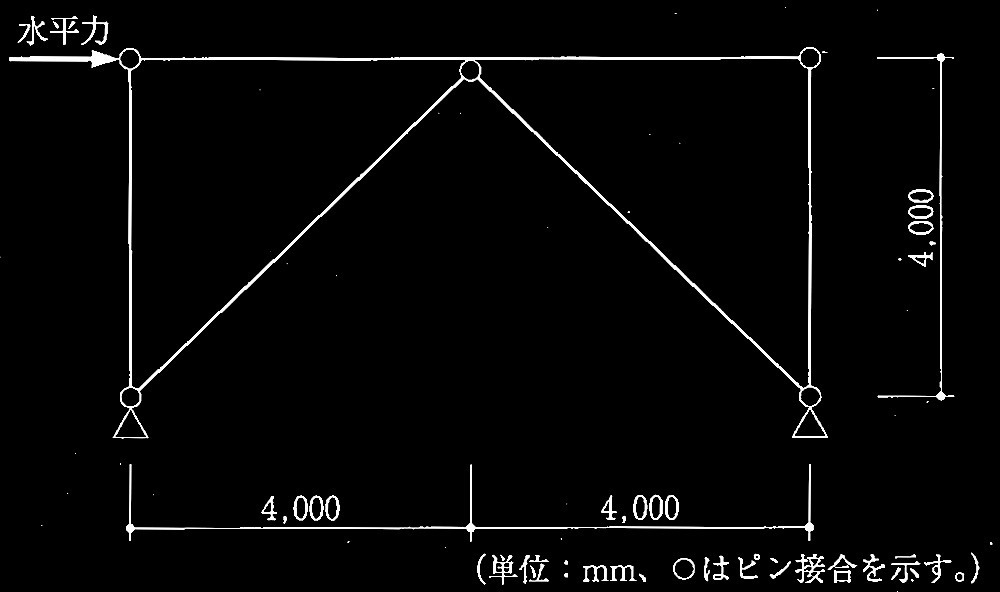
[ No.1 ]
本架構の引張筋かいの終局引張軸耐力を求めよ。なお、終局引張軸耐力は母材の短期許容引張軸力 N y ( = A・σ y ) とする。解答は単位をkNとし、小数点以下を切上げて整数で示すこと。
答え
[ 解答解説 ]
終局引張軸耐力は、
終局引張軸耐力 = N y
= A・σ y
= 4,000mm 2
× 235N/mm 2
= 940,000N → 940kN
となる。
(問題文に「終局引張軸耐力は母材の短期許容引張軸力 N y
(=A・σ y
)とする」および
「基準強度F=短期許容引張応力度 σ y
= 235N/mm 2
」
との記載があるため、材料強度用の1.1倍したF値は用いず、σ y
の値をそのまま用いた。)
[ No.2 ]
圧縮材の座屈時の材料強度 f c は式(1) で表される。本架構の圧縮筋かいについて、式(1) のf c に断面積Aを乗じた値を座屈時圧縮軸耐力 N c とする場合の N c を求めよ。解答は単位をkNとし、小数点以下を切上げて整数で示すこと。

答え
[ 解答解説 ]
圧縮筋かいの長さLは
L=√ (4,000mm 2
+ 4,000mm 2
) = 5,657mm
圧縮筋かいの両端部は面内並びに面外方向にも材軸直行方向の移動が拘束されたピン固定とすると、
細長比λは λ= L/i y
= 5,657mm/40mm = 141
となる。
限界細長比Λ は問題文の式より
Λ = 1,500/√(235N/mm 2
/1.5) =120
となる。
以上より
λ=141 > Λ=120であるため、
f c
は式(1)の下に示された式を用いて
f c
= { (3/5)/(141/120) 2
} × 235N/mm 2
×1.0= 102 N/mm 2
よって、座屈時圧縮軸耐力応 N c
は
N c
= 4,000mm 2
× 102 N/mm 2
= 408,000N → 408kN
となる。
(問題文に材料強度 f c
との記載があるが、
「基準強度F=短期許容引張応力度 σ y
= 235N/mm 2
」
とあることから材料強度用の1.1倍したF値は用いず、σ y
の値をそのまま用いた。通常は、材料強度の基準強度F値はJIS材であるため1.1倍とした値を用いている。)
[ No.3 ]
本架構の圧縮筋かいについて、終局圧縮軸耐力を座屈後安定耐力N u とする場合の終局圧縮軸耐力を求めよ。なお、筋かいの座屈後安定耐力は、式(2)で評価できるものとする。解答は単位をkNとし、小数点以下を切上げて整数で示すこと。
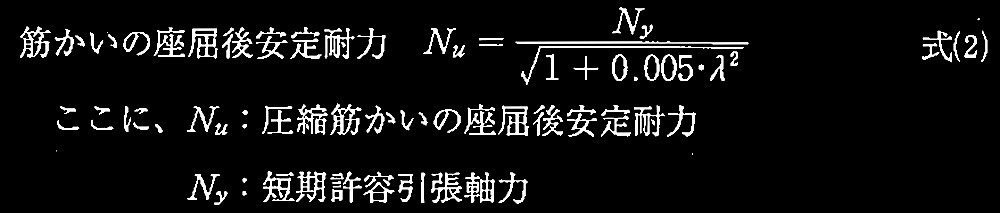
(日本建築学会:建築耐震設計における保有耐力と変形性能(1990)より)
答え
[ 解答解説 ]
筋かいの座屈後安定耐力
N u
= 940kN/√(1 + 0.005 × 141 2
) = 94KN
となる。
[ No.4 ]
水平力を増加させ、引張筋かいが終局引張軸耐力N y に達し、圧縮筋かいが座屈を生じた後、座屈後安定耐力N u となったときの梁の最大曲げモーメントM max を求めよ。また、そのときの曲げモーメント図を描け。ただし、梁は十分な曲げ耐力を有するものとする。曲げモーメン卜図は引張側に描き、M max は単位をkN・mとし、小数点以下を切上げて整数で示すこと。
答え
[ 解答解説 ]
筋かいに生じる軸力は、下図のようになる。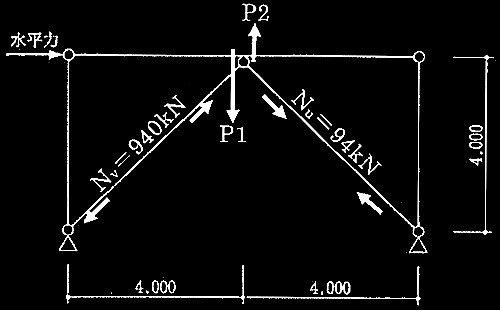
引張筋かいにより梁中央に生じる鉛直力P1ならびに、圧縮筋かいにより梁中央に生じる鉛直力P2はそれぞれ
P1 = 940kN × (4,000mm/5,657mm) = 665kN
P2 = 94kN × 同上=67kN
以上より、梁中央には軸力の変動により
P(下向き) = P1 − P2 = 665 − 67 = 598kN
の鉛直力が働く。
大梁は両端ピン支持の単純梁であるため、この鉛直力に応力は
両端部 Q = 598kN/2 = 299kN
梁の中央に生じる最大曲げモーメントは
M max
= 299kN × 4.0m = 1,196 kN・m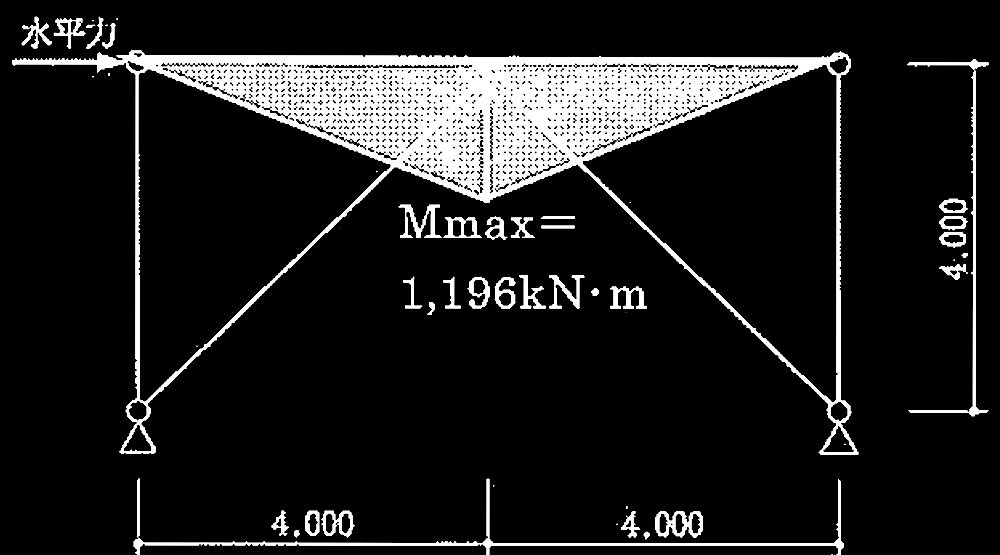
曲げモーメント図
[ No.5 ]
軸力による変動を考慮した梁の全塑性モーメントM p を1,000kN・mとしたときの崩壊メカニズム形成時の保有水平耐力P u を求めよ。なお、圧縮筋かいの軸力は座屈後安定耐力N u とする。解答は単位をkNとし、小数点以下を切上げて整数で示すこと。
答え
[ 解答解説 ]
梁の中央に生じる最大曲げモーメントM p
が 1,000kN・mとなる際に、梁中央に加わる鉛直力Pは
P = 1,000kN・m/4.0m × 2 = 500kN
圧縮筋かいの座屈後安定耐力N u
から梁中央に加わる鉛直力P2は全問のように
P2 = 67kNであるため
引張筋かいから梁中央に加わる鉛直力P1は
P1 = P + P2 = 500kN + 67kN = 567kN
となり、引張筋かいに生じている軸力は
N = 567kN × (5,657mm/ 4,000mm) = 802kN
となる。
崩壊メカニズム形成時の保有水平耐力 P u
は、引張・圧縮筋かいの負担軸力の水平成分の合計であるため
P u
= (802kN + 94kN) × (4,000mm/5,657mm) = 634kN
となる。