問題2
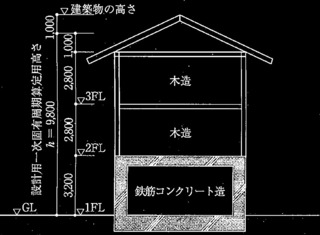
図1に示す2層 1スパンの鉄骨造筋かい付きラーメン構造による建築物に関する次の[ No.1 ]〜[ No.4 ]の設問について解答せよ。本建築物は、図1に示す架構が断面直交方向に2面存在し、各床の剛床仮定が成り立つものとする。表1に構造計算に用いる諸元、表2及び表3に柱、梁及び筋かいの諸元を示す。なお、柱・梁はH形鋼、筋かいは山形鋼とし、柱、梁及び筋かいの鋼種はSN400Bとする。
また、筋かいに長期軸力は生じず、筋かいは圧縮力を負担しないものとする。
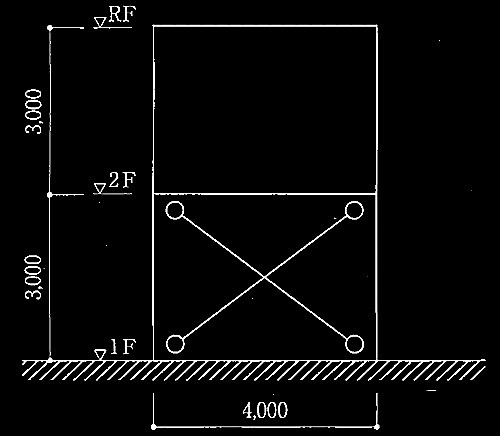
図1 架構の解析モデル図(単位:mm)
表1 対象建築物の構造計算に用いる諸元
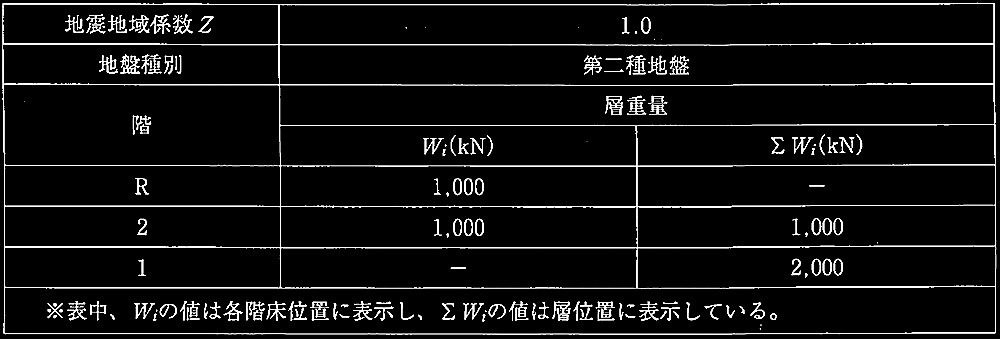
表2 柱、梁の諸元

表3 筋かいの諸元

[ No.1 ]
本建築物に耐震計算ルート2を適用する場合、許容応力度計算において、 各階の層せん断力Q 1 、Q 2 を求めよ。ただし、層せん断力の算定において、標準せん断力係数Coは用い得る最小の値とする。
答え
[ 解答解説 ]
・下記の式にて層せん断力を算定する。
Qi= Ci・ΣWi
Ci = Z・Rt・Ai・Co
・地域係数Zの算定
地域係数 Z = 1.0
・振動特性係数Rtの算定
地盤種別が第二種地盤なので Tc = 0.6秒
建物高さ h = 3m + 3m = 6m
当該建物は 1階、 2階とも鉄骨造なので
設計用1次固有周期を算定する際
α = 1
設計用 1次固有周期
T = h (0.02 + 0.01α)
= 6×( 0.02 + 0.01× 1 ) = 0.18秒
T く Tc より Rt = 1.0
・せん断力分布係数Aiの算定
下記の式にて算定する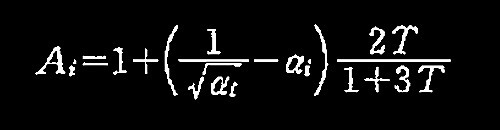
2 階αi = 2 階のΣWi/全体のΣWi
= 1000kN/2000kN = 0.50
1階αi = 1階のΣWi/全体のΣWi
= 2000kN /2000kN= 1.00
2 階の Aiは上式より 1.21
1階の Aiは上式より 1.00
・標準せん断力係数Coの算定
許容応力度計算において用い得る最小の値なので Co = 0.2
・各階の地震層せん断力係数Ciの算定
2 階:Ci = Z・Rt・Ai・Co
= 1.0 × 1.0 × 1.21 × 0.2 = 0242
1 階:Ci = Z・Rt・Ai・C0
= 1.0 × 1.0 × 1.00 × 0.2 = 0.200
・地震力 Q 1
およびQ 2
の算定
2 階 Q 1
= Ci・ΣWi = 0.242 × 1000kN = 242 kN
1 階 Q 2
= Ci・ΣWi = 0.200 × 2000kN = 400 kN
[ No.2 ]
本建築物に耐震計算ルート2を適用する場合、許容応力度計算において、[ No.1 ] にて算出した層せん断力に対する筋かいの短期設計用軸応力Nを昭和55年建設省告示第1791号第2第一号に示す表の数値を考慮して求め、令第82条第三号の規定に適合するか判定せよ。なお、建築物の層せん断力に対する筋かいのせん断力負担率は90%とする。
答え
[ 解答解説 ]
・筋かいの短期設計用軸応力Nの算定
筋かいの負担せん断力
筋かいは建物の 1階に2面存在し、
また圧縮力を負担しないため、地震時に有効な筋かいは
2面 × 1台 = 2台
建築物の層せん断力に対する筋かいの
せん断力負担率は90%であるため、
2 台の筋かいが負担する地震力は
Q 1
×0.90=400kN × 0.90 = 360kN
1台の筋かいが負担する地震力は360kN/2台 = 180kN
昭和55年建設省告示第1791号第2第一号
に示す表の数値を考慮する前の筋かいの軸応力
筋かいの長さはスパン 4m、高さ 3mより
√( 4 2
+ 3 2
) = 5m
1台の筋かいの軸応力 = 180kN × ( 5/4 )=225kN
昭和55年建設省告示第1791号第2第一号
に示す表の数値を考慮した筋かいの軸応力N
建築物の層せん断力に対する筋かいのせん断力負担率 β = 0.90
下表より β > 5/7 より筋かい軸応力の割り増し係数=1.5
表
筋かいの短期設計用軸応力
N=225kN × 1.5 = 338kN
・令第82条第三号の規定に関する検討
筋かいの短期許容軸応力
= 筋かいの基準強度 × 有効断面積
= 235N/mm 2
× 1,289mm 2
= 302915N → 303kN
筋かいの短期設計用軸応力Nが短期許容軸応力を上回っているため、 令第82条第三号の規定に適合しない。
[ No.3 ]
本建築物に耐震計算ルート3を適用する場合、保有水平耐力計算において、各階の形状 係数F es1 、 F es2 を令第82条の6、昭和55年建設省告示第1792号第7に従い求めよ。ただし、[ No.1 ]にて算出した層せん断力に対する2階の層間変形は1階の層間変形の3倍とし、偏心率に応じて求められる各階のFeは1.0とする。
答え
[ 解答解説 ]
・各階のFsの算定
1階の層間変形角を 1/X と仮定する
2階の層間変形は 1階の層間変形の 3倍であり、
1階と 2階の階高は同じであることから、
2 階の層間変形角は 3/X となる。
各階の層間変形色の逆数 rs は下記となる。
2階:X/3
1階:X
rs の相加平均 rs
= ( X/3 + X )/2 = 2/3 X
剛性率Rs = rs/ rs
より各階の Rs は下記となる
2階:Rs = (X/3)/(2/3X) = 1/2 = 0.50
1階:Rs = (X)/(2/3X) = 3/2 =1.50
Fsは昭和55年建設省告示第1792号第7の表にて算定する。
2階:Rs く 0.6 であるため、
Fs = 2.0 − Rs / 0.6
= 2.0 − 0.5 / 0.6 = 1.17
1階:Rs ≧ 0.6 であるため、
Fs = 1.00
・各階の Fes の算定
Fes = Fe × Fs
Fe は1.0であることから各階のFesは下記となる。
2階:Fes2 = 1.0 × 1.17 = 1.17
1階:Fes1 = 1.0 × 1.00 = 1.00
[ No.4 ]
本建築物に耐震計算ルート3を適用する場合、保有水平耐力計算において、昭和55年建設省告示第1792号第3に従い、筋かい並びに柱及び梁の部材群としての種別を判定し、各階の構造特性係数D s1 、D s2 を求めよ。ただし、各階梁の部材種別はFA、組立材としての筋かいの細長比は253とし、架構は水平力に対して引張筋かいの引張降伏後、各階の梁両端部と1階柱脚部母材に曲げ塑性ヒンジが形成される全体崩壊系のメカニズムとなるものとする。また、1 階の保有水平耐力に対する筋かいの水平耐力の割合は60%とする。
答え
[ 解答解説 ]
・筋かいの種別の判定
筋かいの細長比は253
基準強度F = 235N/mm 2
1980/√F=129 ≦ λ = 235 なので下表より筋かいの種別は BB となる。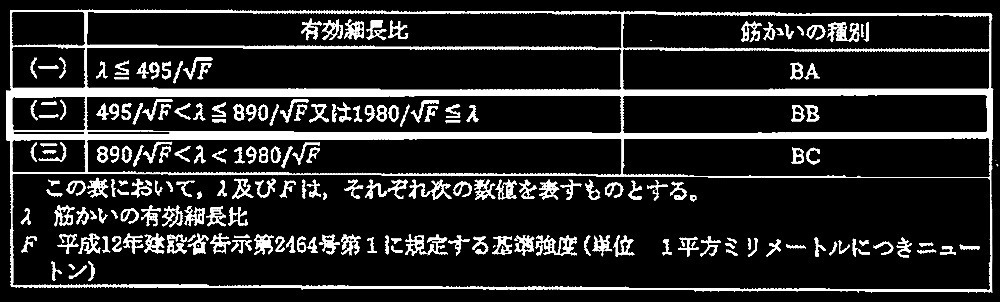
・筋かいの部材群としての種別の判定
筋かいの種別がBBであることから下表のγ A
及びγcは0となる。
従って、筋かいの部材群としての種別はB となる。
・柱及び梁の部材としての種別の判定
梁はFA
柱は H-300 × 300 × 10 × 15
フランジ幅厚比 10 ウェブ幅厚比 27
基準強度 F=235N/mm 2
であることから、
下表より FB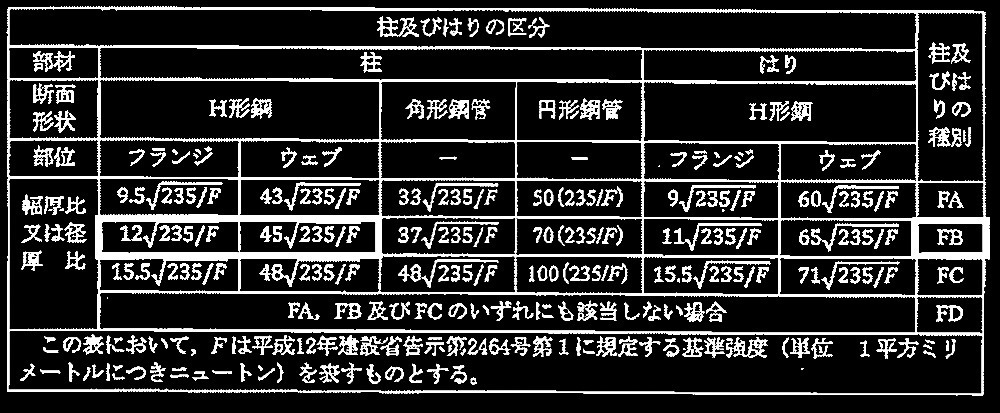
・柱の種別の判定
2階:梁両端部に曲げ塑性ヒンジが形成されることから
梁の種別を採用しFA
1階:柱脚部母材の曲げ塑性ヒンジが形成されることから
柱の種別を採用しFB
・柱および梁の部材群としての種別の判定
2階:全ての柱の種別が FAなので
γ A
= 1.0 γc =0.0 から下表より A
1階:全ての柱の種別が FBなので
γ A
= 0.0 γc =0.0 から下表より B
・ Dsの算定
2階:柱及び梁の部材群としての種別 A
筋かいはないのでβu=0
従って下表より Ds = 0.25
1階:柱及び梁の部材群としての種別 B
筋かいの部材群としての種別 B
保有水平耐力に対する筋かいの水平耐力の割合は60%なのでβu=0.6
従って下表より Ds = 0.30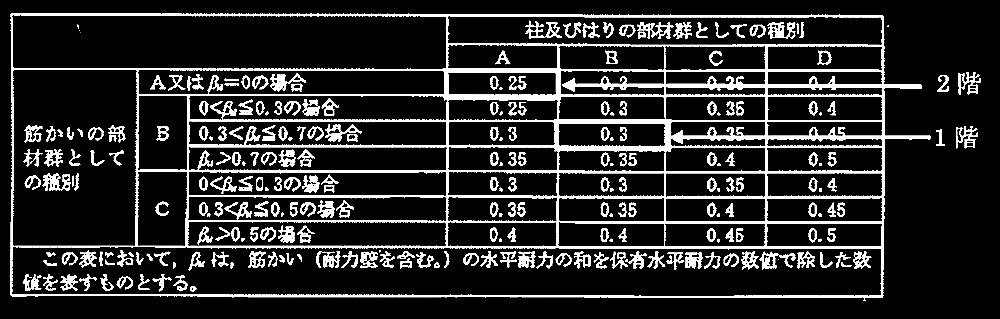
問題文には、柱脚のアンカーボルトの伸び能力の有無、αを考慮した柱脚の保有耐力接合の判定について記述が無いが、保有耐力接合と満足していると仮定した場合、 Ds の割増しは考慮しないとし 1階の Ds は 0.30 となる。
- no image