全323件 (323件中 1-50件目)
-
ナンバーズ3、今週2つめのストレートが当選しました(^.^)
7月2日に書いた数字から、また当選数字が出ました!再掲すると「2.火曜日~金曜日が賞味期限の予想数字です。025 026 035 036 205 206 235 250 253 335 350 352 360 362 363 502 503 520 523 530 532 533 602 603 620 623 630 632 633055 056 065 255 256 355 365 505 506 525526 535 536 562 563 625 635 636 650 660662 663(以上51点)」と書きました。このうちの 055 が本日の当選番号です。これでナンバーズ3の今週の成績は 2勝2敗 になりました。明日はどうでしょう?今、ポアッソン分布で予想できるかな? などと試験しています。そんなに難しく考えなくて問題はありません。これはあくまでも僕の個人的研究に過ぎませんので・・・でも、世の中の動きは、このポアッソン分布に影響されているように見えてなりません。参議院選挙など、まさにこの好例になります。株価も同様の動きをしているものが多いと見受けられます。いずれ、この日記に分析結果を書こうかと思います(^.^)
2007.07.05
コメント(0)
-
ナンバーズ3と4の両方に当選(^.^)
◎ナンバーズ4の本日の当選数字は0454でした。今日の昼に書いた日記の中に、このボックス数字があります。1.すぐに出るかも数字群(週前半)4037 4038 4042 4043 4045 4046 4056 40673.待伏せするといいかも数字群(週央)3766 4405 4406 4436 4506 4536 4626 4636の2つに入っていますね(^.^)◎ナンバーズ3の当選数字は447でした。1.今週いっぱいが賞味期限の予想数字です。044 112 114 115 117 118 121 124 141 142144 145 147 148 151 154 171 174 181 184214 241 244 404 411 412 417 418 421 440441 442 445 447 448 451 454 474 481 484511 514 541 714 744 811 814 841 844 (以上49点)の中に当選数字がありますね。月曜日からシナリオどおりの数字が出ています。◎もし、このブログを見て当選数字に投票した方がおられたら、おめでとうございました。とりあえず、当選報告をお伝えしました(^.^)
2007.07.02
コメント(0)
-
ナンバーズ4にサインが出た
最近、日曜日の日課のひとつとなっているのは、ナンバーズの週間予想を作ることです。ある仮定のもとに5日先の未来まで行ってきて、三段論法でシナリオを作るというわけです。未来を見てくるというまるでタイム・トラベルのような感覚になります。数学の世界は時間の移動が簡単にできてしまいます。これを勝手に「シナリオ法」と命名しています(^.^)すると、ナンバーズ4に異変が起きていました。あるサイン(兆候)が点灯しているのです。勝手に作った関数式です。ある数の組合せが不足したときに教えてくれる関数で、その値が極小値になっていました。この数字は、もう一段進むと、経験上ほぼ98%の確率で出現します。・・・などと、いろいろなシナリオを考えて、次のように1週間分の予想数字をつくりました。毎日微調整していきますが、こんなタイプの数字が出現しやすいというイメージを持つために、目安としての数字群を書き出すわけです。使い方は、1 → 2 → 3 の順にシフトしていきます。1が出たら2へ、2が出たら3へ・・この順番で出てくれると理想的です。1.すぐに出るかも数字群(週前半)1006 1008 1015 1016 1026 1027 1033 10351036 1037 1038 1045 1046 1056 1057 10661067 1068 1108 1127 1137 1138 1192 12131216 1233 1236 1237 1243 1246 1266 12771293 1296 1316 1336 1338 1343 1345 13461356 1367 1368 1378 1396 1408 1427 14371442 1443 1493 1927 1938 1992 4003 40054006 4008 4023 4026 4027 4033 4035 40364037 4038 4042 4043 4045 4046 4056 40674068 4078 4233 4236 4237 4243 4245 42664267 4277 4293 4296 4335 4336 4337 43384346 4356 4357 4366 4367 4368 4377 43784393 4395 4396 4427 4437 4438 4492 44934927 4937 4938 4992 4993 9237 9267 92779367 9378 9927 (以上115点)2.いきなり出るかも数字群(週前半)1008 1027 1037 1038 1057 1148 1167 11781198 1237 1277 1338 1378 1448 1457 14671468 1478 1497 1498 1607 1608 1637 16381677 1678 1756 1766 1866 1967 1968 19781998 4008 4027 4037 4038 4078 4277 43374338 4377 4378 4457 4467 4468 4478 44974498 4537 4577 4607 4608 4627 4637 46384677 4678 4756 4766 4866 4957 4967 49684977 4978 4997 7871 7874 9237 9277 93789627 9637 9677 9756 9766 (以上77点)3.待伏せするといいかも数字群(週央)1105 1106 1126 1136 1405 1406 1426 14351436 1506 1536 1606 1626 1926 1936 20672367 2677 2766 3057 3367 3677 3678 37563766 4405 4406 4436 4506 4536 4626 46364926 4935 4936 5077 5700 6077 6078 67007056 7066(以上42点)なお、この数字でエントリーする物好きな方がしても、当方はその結果に一切責任を負いません(^.^)ところで、ナンバーズ3の方は、平均化しているので、予想作業はあまり楽しいものではありませんでした。それでも、今日出そうな数字のスタイルは見えました。友人にその数字を伝えているので、残念ながらここでは掲載できません。そこで、それ以外の数字を作ってみました。1.今週いっぱいが賞味期限の予想数字です。044 112 114 115 117 118 121 124 141 142144 145 147 148 151 154 171 174 181 184214 241 244 404 411 412 417 418 421 440441 442 445 447 448 451 454 474 481 484511 514 541 714 744 811 814 841 844 (以上49点)2.火曜日~金曜日が賞味期限の予想数字です。025 026 035 036 205 206 235 250 253 335 350 352 360 362 363 502 503 520 523 530 532 533 602 603 620 623 630 632 633055 056 065 255 256 355 365 505 506 525526 535 536 562 563 625 635 636 650 660662 663(以上51点)2.は真ん中で微妙に区切ってあります。区切りより上の方が出やすい数字という意味です。1.2.とも、待伏せるというイメージの数字群です。どちらかひとつに絞って待伏せると効果があるかもしれません。以上、今週のナンバーズ3、4予想をお伝えしました。
2007.07.02
コメント(0)
-
ナンバーズ4、今日は何が出る?
今回は、ナンバーズ4の予想です。ボックスで検証しています。なぜなら、ストレートは当選金額が100万円程度でそれなりに大きいのですが、当選確率が1万分の1・・・これでは、かなりリスキーな予想しか立てられません。まだ、実験していませんが、どうしてもストレートを狙いたければ・・仮説ですが・・ダブルで待伏せをする作戦が有効なのではないかと想像できます。ところで、仮説の何割が実証されればいいかという話で吉四六(きっちょむ)の原則というのがあります。仮説は6割が実証されればOKなのです。これが10割であると、当たり前のことを仮説でわざわざ実験する意味がないとみなされてしまいます。そして、残りの4割にスポットを当てて、そこからまた新しい発見をしていくというのが、統計調査の伝統的なノウハウです。この6割-4割の割合から「四六」、それを「吉」とするから「吉四六」といわれます。◎前置きはこれくらいにして、本日のナンバーズ4の予想結果を発表しましょう。仮定法未来で予想してみたら、以下の60点が候補として現れました。1037 1038 1046 1056 1057 1067 1068 1078 1095 1096 1236 1237 1246 1267 1293 1296 1345 1346 1356 1367 1368 1378 1396 1407 1408 1427 1437 1438 1492 1493 1927 40264027 4035 4036 4037 4038 4056 4057 40674068 4078 4236 4237 4267 4268 4293 4356 4357 4367 4378 4396 4927 4937 4938 9236 9267 9356 9367 9368 「ダブルは来ない」という前提です。引っ張りが少なくとも4回に3回は起きるので、それを考慮に入れたらもっと絞り込めますね(^.^)
2007.06.29
コメント(0)
-
ナンバーズを楽しもう~その3
少ない資金でナンバーズを楽しむには?候補を絞って待伏せするのがいいでしょう。絞るといっても最低でも20点前後で待伏せしないと、かえって効率が悪くなります。どう絞り込めばいいの?どんなシナリオを描くか、それが勝敗の分かれ道になります。シナリオは3つぐらい作ると、どれかが当たります。時間を無視すれば、どれかがいずれ出現します。それでは時間とお金の効率が悪いのでは?時間とお金を最小にして、当選金を最大にするという最大・最小問題です。予想には、常にこの問題がつきまといます。技術進歩関数というのがあります。生産力は資本、労働力のほか技術力によって決定されます。なので、時間関数にして、さらに技術力(ナンバーズの場合は経験値)という外生変数を入れるというイメージです。予想する場合、だれでも自然と「これが出ないとこうなる」「あれが出るとこうなる」という時間軸を使うことになります。このシナリオを作ることこそが、ナンバーズの楽しさなのだと思います。☆昨晩、ナンバーズ3の過去データを見ていて気になることがありました。数0があまり出ていない!ということです。なので、この反動が近いうちに起こりそうです。023 033 034 035 036 037 043 047 054 056065 067 073 074 076 230 320 330 340 350 360 370 403 430 450 470 503 504 506 530 603 630 650 670 730 740 760 0に絡んだ数字が出るとしたら、今日・明日の期限付きでこの37点が有力です。こういったシナリオをあれこれと考えるのが、ナンバーズの楽しさであると思います(^.^)
2007.06.28
コメント(0)
-
ナンバーズ3のストレートが当たりました!
予想数字が当選していました。前回の日記で掲載した予想数字のうち、482なので、攻撃型予想の方が当たりました(^.^)まだまだ予想法は開発途上ですが、当選すると嬉しさもひとしお。整数の世界はとても美しいもの・・・そう感じられるから予想も苦になりません。482は、オール偶数で美しい形です。4=2+28=3+5偶数は素数の和で表せます。不思議です(^.^)
2007.06.27
コメント(1)
-
ナンバーズ3、こんな数字が出るかも?
ここのところナンバーズ3で気になる数字があります。非対称的な出方をする典型的なサンプルとして、「もし今日出現するとしたら」と仮定して予想数字を出してみました。☆賞味期限は今日だけの超予想数字です。1.慎重に予想したら・・・027 037 067 072 073 076 077 227 237 270 272 273 276 278 287 327 370 372 387 627 670 730 732 738 770 837 872 873(28点)2.攻撃的な予想では・・・074 127 138 183 217 218 248 274 279 281 284 297 381 427 437 438 472 473 482 483712 729 734 842(24点)数字を絞り込んであるので、今日だけの予想数字になっています。でも、この形はいつ出てもおかしくないほど出ていません。変な日本語になりましたが、それだけ置き去りにされている数字たちです。※万が一、この数字でエントリーする物好きな方がいても、当方はその結果に一切責任を負いません(^.^)
2007.06.27
コメント(0)
-
ナンバーズを楽しもう~その2
ナンバーズ3は絞込み過ぎて、あえなく敗退(-_-;)925が当選番号だったので、強がりで言えば 279 297 792の3つが数字の組合せとしてはニアピンでした。ナンバーズに実際にエントリーするかどうかは問題ではありません。それよりも、予測する脳力を磨くという観点から、僕は取り組んでいます。そんなレベルの予想ですが、「これは来る!」と思える日が週に何回かやってきます。例えば、ナンバーズ4のデータを見ると、近いうちに次の数字が絡む数字が当選数字になると予想できます。05 06 25 26 35 36の6組の数字です。話を単純化するため、ボックス当選狙いで考えてみましょう。05の組なら 10H2 =11C2=55通りに絞ることができます。他の組も同じなので、55×6=330通り・・・ブーッです。重複している数字がありますね。0506と0605のようなケースです。なので、結論をいえば、245通りになります。そして、このうち実現しそうもない候補には退場してもらいます。まず、4桁の数字の和で絞り込む方法が有名です。奇数や偶数に着目して絞り込む方法もあります。引っ張り現象が頻繁に起きるのがナンバーズ4の特徴なので、引っ張り数字だけに絞る方法が有力です。※引っ張り(引き)とは、今回の当選数字が1234の場合、次回の当選数字に1 2 3 4のどれかが含まれるという現象です。確率で計算してみると4回に3回、ないし5回に4回、この現象が現れます。僕の予想法では180点ほど候補が残りました。これでもまだ多いので、シングルかダブルか、それで選別したりして、最終的に80点程度に絞込み、曜日別に分けます。今気になるのは、55 56 66 の組合せです。この組合せの出現する回数がかなり不足しているのです。すると、05 06 25 26 35 36 とミックスして、0556 や 0566 のような数字が近い将来に出るのでは? と予想できます。おそらく、このミックスした数字は来週前半までに出現することでしょう。こんな具合に、将来起こりそうなことを予測する脳力が鍛えられる・・・これがナンバーズ予想の最大のメリットと思います。算数や数学を学ぶ目的も、まさにこの予測する脳力を磨くことにあります。こどもたちから「数学を勉強して何の役に立つの?」と聞かれることがありますが、数式モデルをつくって将来を予測するため、と第一に答えます。世の中の現象に対して仮説をつくり、データを数値化して数式モデルをつくり、テストする・・・このテストの結果をフィードバックしてモデルに改良を加えていく。このような脳力が21世紀の主役となるこどもたちに必要不可欠と思います。自分でモデリングしないまでも、将来を予測する脳力は生きるために必要です。算数・数学は紙と鉛筆があれば、いつでもどこでも実験できます。このように手軽に脳力アップができる勉強は、ほかにはありません。では、「役に立たないのでは?」とこどもたちが思い込むのはなぜ?原因は、教える側にあります。今日はここまで(^.^)
2007.06.27
コメント(0)
-
ナンバーズを楽しもう!
2年ぶりに帰ってきました。今、高校生の数学を教えるのがメインになってしまい、大好きな算数はご無沙汰しています。その代わりと言っては何ですが、友人からナンバーズ攻略法を考えて・・・と頼まれ、いろいろと試行錯誤しています。ナンバーズが宝くじであることも、つい最近まで知りませんでしたので(-_-;)ロトやミニロトというのもあるそうですが、ロトの場合、当選確率が、ざっとですが600万分の1・・・これじゃ、ほんとに「賭け」です。その点、ナンバーズは賞金がはるかに少なめですが、当選確率はナンバーズ4のストレートで1万分の1、ナンバーズ3に至ってはストレートで1000分の1なので、数学的に面白い研究対象になります。話し変わって、確率論はトランプゲームに勝つために研究された分野です。そして、数字だけの世界なので、ナンバーズ3と4を同時に分析していますが、どちらも予想しやすいと感じています。先週は・・・・ナンバーズ4のボックスが2回連続で当選しました。また、ナンバーズ3のストレートが1回当選しました。研究段階で、まだ買っていないのが悔しいのですが、お金に関係なく、当たると嬉しいものです。友人にもこの予想法を少しずつ伝えていますが、要は数学の応用です。それで、当選確率を上げる作戦とは?確率変数として何を採用するか、ここが肝です。精度の高い変数を見つけられたら、あとは正規分布モデルをつくり、「大数の法則」に従って予想していけばいいだけの話です。予想法はとてもシンプルですが、数字で予想するのはほんの一部です。ちなみに、変数xは秘密です(^.^)今回、超予想してみました。今日は火曜日、締め切りまでわずかの時間しかありませんので、参考に見ておいてください。☆ナンバーズ3の超予想☆138 183 279 297 347 381 437 438473 483 729 734 813 834
2007.06.26
コメント(1)
-
応用自在算数問題集マラソン(22)
☆☆☆がんばれ小学生!★★★ 応用自在算数問題集マラソン(22)明日から新学期がスタートします。と、気分を変えて行こうとしたら・・・英語の宿題をあたためていた子が1名いました。大切にするものがちがいます(-_-;)こうして、きょうは、宿題を仕上げていない子向けの講義になりました。★ ★ ☆ ☆ 今日の講義 ☆ ☆ ★ ★きょうと次回は、応用自在20ページの[21]です。わかる!できる!応用自在問題集 算数ロビン「比例の関係は、魔法の式で表すと?」マック「それじゃ、じゅもんを唱えよう。魔法の式よ、出でよ!」●×▲=■●はいつも同じ数、魔女のモニカ●は変わらない・・・魔法のつえ▲が2倍になったら、クララ■も2倍。魔法のつえ▲が3倍になったら、クララ■も3倍。●はいつも同じ数だから、「比例定数」と呼びます。そして、比例の関係は■=●(比例定数)×▲と表すのがふつうです。ロビン「すると、●×▲=■で表されるかどうか、これを最初にチェックすればいいんだね。」マック「そうだよ。次に、●の位置に比例定数がきているかどうか? これをチェック!」☆表をつくってみると、もっと感覚的に分かります。表づくりは慣れないとむずかしいでしょう。でも、前にも言ったように、線分図をかいたり、表をつくったりしているうちに、問題の意味が読み取れてきます。逆に、線分図や表のイメージが出てこないというのは、問題の意味が正しく理解できているとはいえません。イメージがとても大切です。このイメージングの作業は、空間の図形を扱うときにとても役に立ちます(^.^)[ささやかな宿題](1)三角形の面積は 面積=底辺×高さ÷2 で出てきますね。では、三角形の面積で、比例するのはどれとどれでしょう?(2)半径が2倍になると、円周の長さは( )倍になります。また、円周の長さが3倍になると、半径は( )倍になります。※次回は、反比例のお話に入ります。
2005.08.31
コメント(2)
-
応用自在算数問題集マラソン(21)
☆きょうは、表をつくって考えるワークをします。「表」がつくれる、つくれない・・・これはサイエンスの世界ではとても大切な能力です。算数でも理科でも社会でも、表をつくると分かりやすくなります。実際、書いたもん勝ちです(^.^)でも、1回目にかんぺきな表をつくることは無理というもの。だから、どんな表でもいいんです。書いているうちに、何かが発見できます。書いているうちに、表も改良されていきます。さあ、力を抜いて・・・まちがってもいいから表をつくりましょう。この行動力の差が、算数などのサイエンスでは後々、決定的な差につながっていきます。☆☆☆がんばれ小学生!★★★ 応用自在算数問題集マラソン(21)[宿題の解説]ダイヤグラムで考えた子はいますか?ロビン「ダイヤグラムをかいたけれど、うまくいかないね。」マック「そんなときは、見通しをよくするために表をつくってみると、手がかりが得られるかもしれないよ。」(1)そこで、ロビンは次のような表をつくりました。 行き 帰り予定より短くなった時間 20分 45分その対象となるきょり 40km ( )kmロビン「この区間は速さ一定!すると、時間の比がきょりの比と同じになるはず。」一定を使っていますね(^.^)20分:45分=40km:( )km( )=45×40÷20=90ロビン「90kmになった!これが60%にあたるから、90÷0.6=150km。これが答え。」これで、(1)の関門を通過しました。(2)全体の距離が分かったので、ここからは楽です。もしも、もしもの考え方でいきましょう。ロビン「もしも時速30kmで150kmを進んだら、5時間かかるな。でも、40kmだけ、もっとはやく進んだので、25分短くなった・・・待てよ、40kmの区間だけで調べてもいいはず。110kmは時速30kmで進んできたのだから。40km÷30km/時=4/3時間=1時間20分これより20分短いと言うことは、1時間20分-20分=60分 」一息ついて、ロビンは言いました。ロビン「きょり一定だから、時間の比の逆比が、速さの比になる。」1時間20分:60分=80:60=4:3時速30km:時速( )km=3:4ロビン「( )の中は40だ!」答えは 時速40km「もしも、もしも」や「一定」・・・こんな言い回しを覚えておくと、きっと役に立ちます(^.^)☆さて、次回から2回連続で、応用自在20ページの[21]の講義をします。数の関係では、中学数学に一番近い比例と反比例の関係です。2つの変量(変数)の関係は、ある条件を満たすと、比例や反比例になります。特に、反比例の関係は、グラフにするととても美しく見えます。このセンスが大切です。グラフに慣れてくると、正しいものが美しく見えはじめます。美しいグラフにならないと、なにかがまちがっている可能性があります。解答も美しく、そしてシンプルでなければ、やはりどこかがちがっている場合が多いのです。たとえば、天動説で惑星や星の動きを説明しようとすると、とても複雑なシステムを考えるハメになります。でも、いくら複雑にしても、すべての星の動きが説明できず、かなり苦労したあとがみられます。ところが、地動説にして太陽を中心にすると、とてもシンプルなシステムで説明できてしまいます。描かれる星や惑星の動きも、美的です。本物は、いつだって、シンプルで美しい。こんなことを、頭のかたすみに入れておいてくださいね。(つづく)
2005.08.30
コメント(1)
-
応用自在算数問題集マラソン(20)
☆きょうは応用自在問題集の解説編です。比や逆比が飛び回ります。でも、どれが比でどれが逆比か、はじめのうちは混乱するかもしれません。そこで、口ぐせにしてほしい言葉を覚えてもらいます。この言葉がすぐ出るようになるまで、声に出して練習しましょう(^.^) ☆☆☆がんばれ小学生!★★★ 応用自在算数問題集マラソン(20)★ ★ ☆ ☆ 今日の講義 ☆ ☆ ★ ★今日は、応用自在20ページの[20]をいっしょに勉強していきましょう。わかる!できる!応用自在問題集 算数ゴールの問題は、比で解きます。時計の遅れや進みも、比の問題ですね(^.^)マック「次回の講義の比例・反比例にも関係してくるけれど、ロビンに覚えてほしい言葉があるんだ。」ロビン「式ではなくて、言葉・・・」マック「式も言葉も元は同じ。だから、式もできるだけ言葉で表現してみると、式の本質が見えてくるよ。」ロビン「マック先生、その言葉って何?」マック「一定! ●×▲=■ の中で、何かが一定のときに、比例や反比例という現象が起きる。」ロビン「一定・・・いつも同じということだね。」マック「一定なものは、きみには動かすことはできない。たとえば、あるきょりを往復する問題なら、きょりが一定さ。かべに打ちつけた釘のようにね。」ロビン「釘のようになったきょりは動かせない。動かせるのは、速さと時間だね。」マック「これが反比例の関係。比の世界なら逆比さ。」☆きみに覚えてほしい言葉一 定 比や比例の世界では、何が釘になったのか 気をつけないと、まったく逆のことをしてしまう。 口ぐせのように「○○一定」とつぶやいて、 問題にとりかかろう(^.^)(学校で声に出すと、あやしまれるかも・・・) (1)きょり一定なので、時間の比から速さの比は、すぐに求まります。(太郎君の速さ):(お兄さんの速さ)=□:□このことから、お兄さんが100m走ったとき、太郎君は□m走ることがわかります。(2)時間一定ですね。 すると、速さときょりの( )は等しくなります。このことから、まず速さの比を求めます。(太郎君の速さ):(お兄さんの速さ)=□:□次に、「同時にゴールイン」するので、再び、時間一定の世界です。ロビン「だから、速さの比からきょりの比が出てくるんだね。」マック「次の問題から、比例・反比例の関係に入るよ。」ロビン「予習しておこうかな・・・」[宿題]A町とB町の間を時速30kmで往復する予定でしたが、行きは途中40kmの長さの区間を速度をはやめて走ったので予定より20分早く着きました。帰りは60%の区間を、行きにはやめた速度と同じ速度で走ったので、行きにかかった時間よりさらに25分短い時間で着きました。次の問いに答えなさい。(1) AB間は何kmありますか。(2) はやめた速度は時速何kmですか。 (独協中)
2005.08.29
コメント(0)
-
応用自在算数問題集マラソン(19)
☆もうじき学校が始まります。各学年とも、学習内容が佳境に入っていきますね。この問題集マラソンも、今回から隔日で 応用自在 → 累題演習と繰り返していきます。じっくりと力をつけていきましょうね(^.^)☆☆☆がんばれ小学生!★★★ 応用自在算数問題集マラソン(19)[宿題の解説]ダイヤグラムを描きながら解くのが、一番素直です(^.^)でも、ここでは比の練習なので、比を使って解きましょう。マック「時速60kmの速さ と 時速40kmの速さの速さの比は?」ロビン「60:40=3:2 だよ。」マック「では、時間の比は?」ロビン「きょりが一定だから、 2:3!」マック「時間の差はどれだけあるかな?」ロビン「30分と1時間の合計で1時間30分。そうか! 比の差が1時間30分にあたるんだね。比の2を(2)比の3を(3)と表すと(3)-(2)=(1)この(1)が1時間30分にあたる!!!」マック「すると、(2)は何時間何分のこと?」ロビン「1時間30分×2=3時間0分だから・・・時速60kmなら3時間かかるということだね(^.^)そして、予定の時間は3時間30分。マック「まず、道のりから求めよう。」ロビン「時速60km×3時間=180kmこの道のりは 180km あるんだ!!」>この道のりを、時速50kmで3時間進みました。マック「何km進んだことになる?」ロビン「時速50km×3時間=150kmまだ、180-150=30kmも残っているね。残りの時間は30分。30km÷0.5時間=60km 」答え 時速60km■明日の学習範囲□ 応用自在20ページの[20]力をつけるために、予習しておきましょう(^.^)
2005.08.28
コメント(0)
-
応用自在算数問題集マラソン(18)
☆友人のKさん、映画プロデューサーですが、その彼が3日前、駅頭で倒れました。気がついたら救急車の中だったそうです。検査結果待ちですが、映画制作を止めるわけには行かないので、仕事は休めません。こう暑いのでは、体に異常が出てきてもおかしくはありません。規則正しい生活が何よりです。そういう私も、規則正しいかというと・・・(-_-;)☆☆☆がんばれ小学生!★★★ 応用自在算数問題集マラソン(18)[宿題の解説]マック「速さの比と時間の比がヒントだよ。」ロビン「そうか!同じ距離だから(歩く速さ):(自転車の速さ)=1:3 の逆比だ!」(歩いてかかる時間):(自転車でかかる時間)=3:1 ロビン「歩いてかかる時間は45分だから、3:1=45:( )自転車でかかる時間は 15分!だから、自転車の方が30分早く着くはず・・・」マック「でも、その差が12分。ということは・・・」ロビン「30分と12分の差が修理にかかった時間だ!」答え 18分★ ★ ☆ ☆ 今日の講義 ☆ ☆ ★ ★きょうは、応用自在20ページの[19]です。わかる!できる!応用自在問題集 算数これもきょりが一定なので、速さの比と時間の比の逆比の関係を使えばいいのですね。イメージで復習しましょう(^.^)●×▲=■ を使って●×▲=■○×△=■●×▲=○×△●:○=△:▲逆比が分かったら、△:▲=( ):6[宿題]時速60kmの速さで行けば、予定より30分早く着き、時速40kmの速さで行けば予定より1時間おそく着く道のりがあります。この道のりを、時速50kmで3時間進みました。予定の時間に着くには、残りの道のりを、時速何kmで進めばよいですか。 (昭和女子大付属昭和・改題)
2005.08.27
コメント(0)
-
応用自在算数問題集マラソン(17)
☆海岸を散歩していたら、赤とんぼの大群と遭遇しました。夜になると、公園や植え込みから虫の音が聞こえてきます。いつの間にか、秋の気配が色濃くなってきています。まだまだ、残暑が続きそうですが。夜、窓を開けた拍子に、赤とんぼくんが1匹部屋の中に入ってきました。明るいところを目指して飛び回り、天井に安住の地を見つけて休んでいました。やがて、状況をやっと把握できたのか、焦って窓から出て行きました(^.^)☆☆☆がんばれ小学生!★★★ 応用自在算数問題集マラソン(17)[宿題の解説]逆比の問題ですね。4時間を行きと帰りに分けます。ロビン「どのように分ければいいのかなー?」マック「行って帰ってこなくてはいけないよね。」ロビン「ぴったりと元に戻ってくるということだよね。ということは・・・行きも帰りもきょりが同じ!!!」マック「それに気づいたら、つぎは・・・」ロビン「速さの比 50:30 の逆比が時間の比。そうか! 4時間を 3:5(逆比)に分ければいいんだ!」行き 4時間×3/(3+5)=1.5時間帰り 4時間×5/(3+5)=2.5時間行きで調べると50km/時×1.5時間=75km答え 75km[追加の宿題2の解説](1)30分進んで5分休み を (30分,5分)で表しましょう。これを1セットとすると、35分。「3時間(180分)かかった」ということは180分÷35分/セット=5セット あまり 5分ロビン「それじゃ、休んでいた時間は25分。走っていたのは 180-25=155分 だから、答えは 2時間35分 だね。」マック「その通り!(2)ロビン「帰りの速さは行きの5/6だから、速さの比は 6:5時間の比は 5:6あとは、比を使って5:6=155:( )( )=6×155÷5=186分1セットは(40分,8分)だから186÷48=4セット あまり 26分(40分+8分)×4セット+26分=218分!」答え 3時間38分★ ★ ☆ ☆ 今日の講義 ☆ ☆ ★ ★きょうは、応用自在20ページの[18]です。わかる!できる!応用自在問題集 算数線分図をかいて考えましょう。全体の道のりを 1 とおけばいいのですね。(1) 2日目は 残り2/3の3/4 比の積を使います。(2) たとえば最初の200mと次の300mを進むのに、歩く速さの比を 3:2としましょう。すると、かかる時間の比は●×▲=■○×△=□で考えると3×▲=2002×△=300したがって、時間の比は▲:△=200/3:300/2=400:900 =4:9200mと300mを 2と3 としても同じです(^.^)連比をうまく使いましょう。[宿題]歩くと45分かかる道のりを自転車で走っていったところ、道のりを2/3まできたところで故障してしまいました。自分で修理し、残りの道のりを同じ速さで走ったところ、歩くより12分早く着きました。修理にかかった時間は何分ですか。ただし、自転車の速さは歩く速さの3倍でした。 (日本大豊山)
2005.08.26
コメント(1)
-
宿題の追加です
台風接近で、テンションが上がったせいか、宿題をまちがえてしまいました。そこで、宿題の追加です。速さの周期の問題です。[宿題2]自転車でA市からB市へ行くのに、30分走っては5分休んで行ったところ、3時間かかりました。帰りは行きの5/6の速さにして40分走っては8分休みました。次の問いに答えなさい。(1) 行きは自転車で何時間何分走りましたか。(2) 帰りは何時間何分かかりましたか。 (広島学院)
2005.08.25
コメント(0)
-
応用自在算数問題集マラソン(16)
☆台風11号が接近中です。近くの商店街に出かけてきましたが、いつもの賑わいが消え、ひっそりとしていました。マックの塾も臨時休講です。しかし、上の娘カオリンの数学講義があります。積分の「区分求積法と積分の関係」です。ここで使う算数は図形の面積と植木算、中学数学では、文字式の計算、因数分解、高校数学から関数の考え方と、不等式、極限値・・・これらが一体となって、区分求積法ができあがっています。でも、基本は●×▲=■なのです(^.^)だから、魔法の式がわかっている子には、積分法も楽に学べるのです。☆☆☆がんばれ小学生!★★★ 応用自在算数問題集マラソン(16)[宿題1の解説]魔法の式を使います。行き ●×▲=■帰り ○×△=■で表すことにしましょう。●と○は速さ▲と△は時間■はきょり●×▲=○×△=■すると、■を仮に1とおいてもかまいません。●×▲=○×△=1 (あ)▲:△=1/●:1/○=○:●もちろん、(あ)から直接▲:△=○:●としてもかまいません。36:48=○:●つまり、●:○=48:36=4:3答えは 4:3 です。※きょり1.4kmは、別になくてもいいわけです。 [宿題2の解説]こんどは、きょりが出ていません。こんなときは、あわてずに、きょりを 1 とします。すると、時間は 1/● と 1/○合計で 1/●+1/○きょりは 往復なので 22÷(1/●+1/○)=2÷(1/90+1/60)=72答え 時速72km★ ★ ☆ ☆ 今日の講義 ☆ ☆ ★ ★きょうは、応用自在20ページの[17]です。わかる!できる!応用自在問題集 算数「速さの周期算」です。進んでは休み、また進んでは休み・・・このくりかえしの問題です。(歩く時間,休む時間)というように表すことにしましょう。ロビン! 数を入れてみて!ロビン「 (50分,10分) だよ。1時間の組み合わせだね。休みを入れないで歩けば、12km÷3km/時=4時間 でも、4時間のうち歩くのは比例配分の考え方を使って、50÷(50+10)=5/6だから、歩いた時間は4時間×5/6=240分×5/6=200分 」マック「すると、200分で歩いたきょりは?」ロビン「時速3kmは分速で3000m÷60分=50m/分ということは、50m/分×200分=10000m=10kmまだ、2km残っているね。」マック「この2kmを分速50mで歩くと・・・」ロビン「わかった! これで答えが出てくるね。」[宿題]自動車で4時間だけドライブするのに、行きは時速50km、帰りは時速30kmの速さで走るものとすると、何kmはなれたところまで行ってこられますか。(東洋英和女学院)
2005.08.25
コメント(0)
-
応用自在算数問題集マラソン(15)
☆☆☆がんばれ小学生!★★★ 応用自在算数問題集マラソン(15)[宿題の解説](1)比を使って解きましょう。60分で45km□分で18km だから 60分:□分=45km:18km60:□=5:2□=24 答え 24(2)時間の計算です。60進法を使いこなそう(^.^)マック「ロビンの考え方は?」ロビン「1時間21分40秒 が● 60%が▲ 魔法の式にあてはめて ●×▲=■ 1時間21分40秒×0.6=・・・」マック「81分40秒×0.6 にしてもいいけれど、 まだ計算してはダメ!81×0.6 では小数が出てきてしまうね。」ロビン「81分40秒は80分100秒だから 80分100秒×0.6=48分60秒=49分 」 答え 49 (3) 3時間30分で175km進むから 210分で175km 42分で35km 2520秒で35km ここから先は比を使って 2520秒:□秒=35km:1km □=2520÷35=72 答え 72★ ★ ☆ ☆ 今日の講義 ☆ ☆ ★ ★きょうは、応用自在19ページの[16]です。わかる!できる!応用自在問題集 算数2つの速さの平均を求めます。ロビン「つい、2つの速さをたして2で割ってしまうことがあるけれど、これはダメだよね。」マック「実際に問題を解いてみるといいね。2で割っていいのは、特別な場合だけだよ。」(1)時間を追って考えてみよう。 15分間は、15/60時間 時速80kmで15/60時間進むと●×▲=■ から20km と出てくるね。つぎは、時速40kmで1時間だから40kmこれを表にしてみよう!速さ 時間 きょり時速80km 15/60時間 20km時速40km 1時間 40km時間ときょりに注目して1/4時間 20km1時間 40km合計で、時間は5/4時間、きょりは60km●×▲=■ から●×5/4=60●=60÷5/4=48☆ 特別な場合とは、時間が同じとき!速さ 時間 きょり時速80km 1時間 80km時速40km 1時間 40km上のような表の場合合計で、時間は2時間、きょりは120km●×▲=■ から●×2=120●=120÷2=60ロビン「そうか! 魔法のつえ▲が同じときだけ足して2で割っていいんだ!」(2)も時間を追って、表をつくってみよう。 上の段が行き、下の段が帰り だよ(^.^)(3)は別な考え方で解いてみようね。ロビン「それって、むずかしい?」マック「●×▲=■ を利用すればいいのさ。」行きは ●×▲=■ だから ●=■/▲帰りは ○×△=■ だから ○=■/△●と○は速さだよ。▲と△は時間、きょりは同じだから■表をつくってみよう。速さ 時間 きょり● ▲ ■○ △ ■合計で、時間は ▲+△、距離は■+■平均の速さ<●>は<●>×(▲+△)=2×■<●>=2×■/(▲+△)右の辺の分子にある■は分母にもっていくと、<●>=2×■/(▲+△) =2/(▲/■+△/■) =2/(1/●+1/○)ロビン「分かったような気もするけれど・・・」マック「■を1と置いてみると、もう少しかんたんになるよ。」☆ この公式は、速ささえ分かれば、平均の速さが求まるということを語っています。分母の 1/● と 1/○ は時間です。分子の 2 は往復のきょりのことです。[宿題1]家から学校まで1.4kmあります。花子さんは、学校へ行くときに36分かかりました。帰るときは、ゆっくり歩いたので48分かかりました。このとき、往きと帰りの速さをもっともかんたんな比で求めなさい。 (聖心女子学院)[宿題2]次の□に適する数を求めなさい。A町とB町を自動車で往復します。行きは時速90kmで、帰りは時速60kmでした。このとき平均の速さは時速□kmです。 (鎌倉学園)
2005.08.24
コメント(0)
-
応用自在算数問題集マラソン(14)
☆公園を散歩していると、蝉時雨がとどろいていました。夏の一大交響曲のようです。こどもたちが網でつかまえる光景は、昔の自分の姿がタブります。しかし、こういう情緒に浸れるのは日本人の特権。アメリカ人の義姉は、ノイズにしか聞こえないと言っていました。確かに、騒音と思うと、忍耐の必要なものすごいボリュームです(-_-;)アイスキャンデーを咥えて、自転車を駆る男の子とすれちがいました。アイスは、とてもおいしそうでした。こうして、こどもたちの夏休みも、もう少しで終わります。☆☆☆がんばれ小学生!★★★ 応用自在算数問題集マラソン(14)[宿題の解説]ロビン「比の差をすぐ使うのかと思ったら、そうかんたんには解けなかった・・・」マック「いろいろと落とし穴があるんだよ(^.^)でも、入試の前に失敗しておかないと困るんだ。素直なだけじゃ、入試は乗り切れない。」ロビン「女王の教室のようになってきた・・・」マック「入試の季節には、受験生はインフルエンザの予防注射を打つよね。あれと同じ。今、失敗してワクチンをつくっておかないと、本番で失敗するよ。」ロビン「そうか。じゃあ、今のうちに思いっきり失敗しそうな問題をやっておこうかな。」マック「宿題に入るよ。比の差は使えないね。この手の前後のある問題をやるときは、全体は変わったのか? 変わっていないのか?ここに気がつけば、あとは自動ドアのように答えにたどりつくトビラが開くよ。」ロビン「前後? 水を移しているけれど、全体の重さは変わらない・・・・・」はじめ 3:1移した後 4:3ロビン「はじめは 3+1=4移した後では 4+3=7この4と7は、どちらも同じ重さを表している。4と7の最小公倍数は28。わかった!!!はじめは 比を7倍して、 21:7 足して28移した後は 比を4倍して、 16:9 足して28ビーカーAは 21から16に減っている。」マック「ここで比の差が出てきたよ(^.^)」ロビン「仮に21g-16g=5g5gを20倍すれば100gになるから、ビーカーAははじめは 21g×20倍=420g移した後は 16g×20倍=320g!」答え 420(g)★ ★ ☆ ☆ 今日の講義 ☆ ☆ ★ ★きょうは、応用自在19ページの[15]です。 わかる!できる!応用自在問題集 算数どうせ努力するなら、公式を必死になって覚えるよりも、●×▲=■を使って本質をとらえることにしましょう(^.^)速さは 1単位あたりの量時間は その何倍?きょりは 全体の量だから、●×▲=■速さ×時間=きょり覚えるのはこれだけ・・・だよ。(1)は●を求める問題(2)は■を求める問題(3)は●を求める問題(4)は▲を求める問題ここで、時間が60進法であることに注意!マック「時速36kmは分速□m、秒速□mロビン!□に数を入れてみて。」ロビン「時速36kmは時速36000m60分で36000m1分では 36000m÷60分=600mだから、分速600m。1分で600m60秒で600m1秒では 600m÷60秒=10mだから、秒速10m!」[宿題]次の□にあてはまる数を求めなさい。(1)時速45kmで進む車は□分で18km進みます。 (聖学院)(2)1時間21分40秒の60%は□分です。 (江戸川女子)(3)3時間30分で175km進む車は、 1km進むのに、□秒かかります。 (品川女子学院)
2005.08.23
コメント(0)
-
応用自在算数問題集マラソン(13)
☆「もしも、地球に100人のこどもしかいなかったら」「もしも」の世界・・・つるかめ算の解き方で有名です。「もしも、ぜんぶがカメだったら・・・」この考え方は1.仮に、単純なモデル(模型)を つくって、2.実際と違いが出てきたら、その違いを なくすように調整するこのステップで進みます。きょうの講義にも、この「もしも」が出てきます(^.^)あなたのまわりの世界も、「もしも」で見てみると、おもしろい特徴がわかるかもしれません。☆☆☆がんばれ小学生!★★★ 応用自在算数問題集マラソン(13)[宿題の解説]ロビン「昼の長さと夜の長さの比は 5/7:1=5/7:7/7=5:7 全体を12に分けたうちの5つ分が、昼の長さ。 だから、24÷12×5=10 答えは (10)時間( 0)分★ ★ ☆ ☆ 今日の講義 ☆ ☆ ★ ★きょうは、応用自在19ページの[14]です。比の差に注目します。わかる!できる!応用自在問題集 算数(1)の問題は線分図をかいてもいいですね。線分図のかわりに、○で表すと姉 ○○○○○○○○○妹 ○○○○○○○ ロビン「差は○○だね。これが420円にあたる・・・」すると、○は( )円マック「仮のモデルをつくってもいいね。」ロビン「仮のモデルって、つるかめ算もそうだね。」マック「公式に頼らなくても、この「仮」という考え方ができれば、それで解いてかまわない。」☆厳格な私立小学校では、学校で教えた解き方でしか解答を許さないというところもあります。でも、この「仮」という考え方がスムーズにできないと、難問や入試では苦戦しますよ(^.^)たとえば、姉と妹を5:3として、差が120円こんなケースで考えてみよう。仮だから、5円と3円にしてしまうと・・・ロビン「差は2円。でも、実際は120円だから、60倍してあげないといけない・・・」姉 5円×60倍=300円妹 3円×60倍=180円(2)3人の比を出して・・・ロビン「それから、仮のモデルをつくって解く(^.^)」[宿題] □にあてはまる数を答えなさい。ビーカーAとビーカーBに入っている水の重さの比は、はじめ3:1でしたが、ビーカーAから100gの水をビーカーBに移したら、重さの比が4:3になりました。はじめにビーカーAに入っていた水は□gです。 (武蔵工業大学付属)
2005.08.22
コメント(0)
-
応用自在算数問題集マラソン(12)
☆きょうも暑い一日でした。夏休みの宿題は終わりましたか?中学校で2学期制をとっているところは、9月の中旬には前期期末試験が、さっそくあります。その対策もスタートしました。マックのところには、日曜日でもこどもたちがやってきます。もうそろそろ、元気な声が聞こえて来ます(^.^)☆☆☆がんばれ小学生!★★★ 応用自在算数問題集マラソン(12)[宿題の解説]女学院中学の問題です。なかなか、てごわかったかもしれません。ロビンはどうだった?「倍数の考え方に気がつかなかったから、かなり計算が大変。。「商品Bと商品Cのねだんは80円と62円。これを個数3:4の比で買ったから、一番小さな3個と4個買ったとしたんだ。すると80円×3個+62円×4個=488円商品Bと商品Cの合計の代金は、488円の倍数になるって、これでわかった。「それで、商品B3個と商品C4個の詰め合わせを1セットとして、△セット買ったと考えることにしたよ。商品Aは○個買ったことにした。式をつくってみたら37円×○個+488円×△セット=22200円 」マック「なかなか、いい線行ってるよ!問題はここからだね。」ロビン「そうなんだ。ここから先が・・・」マック「22200を37で割ってみて!」ロビン「22200÷37=600 割り切れた!」マック「つぎに、488の方は?」ロビン「488÷37=13 あまり7」マック「37と488は、互いに素の関係にあるよね。ということは、△が37の倍数でないと、式が成り立たない。」△=37×( )ロビン「すると、式は37円×○個+488円×37×( )セット=22200円 」マック「これで、どれも37の倍数になったね。37でそれぞれを割ると・・・」ロビン「○+488×( )=600( )にあてはまる数は 1 しかないなー。」マック「それじゃ、1を入れて!」ロビン「○+488=600○=600-488=112商品Aは112個セットの数は37だから商品Bは37×3=111個商品Cは37×4=148個」比の問題というより、倍数の問題でした。たまには、このレベルの問題を解くのもいいかもしれません(^.^)★ ★ ☆ ☆ ☆ ☆ ☆ ☆ ★ ★きょうは、応用自在19ページの[13]です。比例配分ですね。比を使いこなしましょう。わかる!できる!応用自在問題集 算数(1)全体はいくつに分けられていますか?1本が5つ分と3つ分の8つ分に分けられています。○○○○○○○○差は ○○ です。(2) 時間の計算は60進法ですね。時間の問題は、こんな形でも出てきます。[宿題]( )にあてはまる数を求めなさい。ある日の昼の長さは夜の長さの5/7でした。この日の昼の長さは( )時間( )分でした。 (目白学園)
2005.08.21
コメント(0)
-
応用自在算数問題集マラソン(11)
☆「女王の教室」をはじめて見ました。遅れています(-_-;)心に思っていることをそのまま口にしたらこうなるという、「ほんとにこんなのあり?!」という内容。小学生のこどもたちを相手にここまで言うのも精神が病んでいると感じましたが、テレビなのでドラマ仕立てになっているのでしょう。こういうあり得ない世界を擬似体験させてくれる、という点で、映像の世界は優れています。しかし、進学校や塾の受験クラスのこどもたちの意識、「勉強以外はムダ」・・・この部分は、確かに存在します。あながち、荒唐無稽な世界でもないのです。こういうドラマがテレビに登場するというのはなにか、こどもたちの世界も大人の論理に強く支配されている現代を暗示させます。マーケティングといえば会社だけかと思ったら、学校にもマーケティングの考え方が入ってきています。少子化対策として、学校間相互のこども争奪戦がはじまっているのです。これと軌を一にするかのようなドラマです。学校も、いろいろなサービス、受験に特化する学校とか、起業家をめざすこどもたちを支援するプログラムを提供する学校など、学校自体が生き残りをかける時代に入っていく予感がします。☆☆☆がんばれ小学生!★★★ 応用自在算数問題集マラソン(11)[宿題の解説](1)文章をそのまま式にしてしまいましょう。1000円×0.75=5000円×□5000円×□=1000円×0.75=750円□=750÷5000=15÷100=0.15 答え 15%ロビン「せっかく習ったのだから、逆比でやってみたよ。」1000円:5000円=1:5ということは、0.75:□=5:1□×5=0.75×1□=0.75÷5=0.15ロビンくん、スマートに計算しています(^.^)(2)速さの比が 4:9 だから・・・ロビン「時間の比は 9:4 だね!」この比を使って、時間を○で表すと歩く ○○○○ ○○○○○走る ○○○○差の○○○○○ が10分にあたるから、○ひとつは、 10分÷5=2分ロビン「だから、走る時間は○4こで8分だ!」あとは計算(^.^)9×8/60×1000=1200 答え 1200mおまけの、応用自在P23の[12]はどう?ロビン「3本の棒は、水面の下が同じ長さになっているはず・・・」そこに気がつけば、あとは計算だけだね(^.^)A×(1-1/3)B×(1-1/4)C×(1-1/5)が同じ長さ。A×2/3=B×3/4=C×4/5=1逆数を利用して、比で表すとA:B:C=3/2 : 4/3 : 5/42,3,4の最小公倍数を右の辺にかけて・・・あとは、問題集の答えのとおり。同じページの[10]と[11]も、逆比の問題だよ。★ ★ ☆ ☆ ☆ ☆ ☆ ☆ ★ ★きょうは、応用自在18ページの[12]です。わかる!できる!応用自在問題集 算数(1) ロビンのやり方は、こうです。男の子 ○○○○○女の子 ○○○○○○○○ が 16人 だから、 ○ は 16÷4=4人 クラス全体は ○が9こ 比をビジュアルにして解くやり方です。 こどもたちには、一番わかりやすいやり方です(^.^)<比の利用>比で扱うとしたら、 5:4=( ):16 こうして、男子の人数が出てきます。<魔法の式+比の利用> ●×▲=■ で、 ▲が女の子の割合4/(5+4) つまり、4/9 です。 ●がクラス全体の人数、割合でいえば 1 ですね。 (クラス全体の人数)×(女子の割合)=(女子の人数)(2) 連比の問題です。 A:B:C が求められたら、 ●×▲=■ で解くのが一番速くできます。 この考え方は、次の「比例配分」につながっていきます。[宿題] 次の□にあてはまる数を入れなさい。花子さんは、1個37円の商品Aと1個80円の商品Bと1個62円の商品Cを何個かずつ買いました。値段の合計は22200円で、商品Bの個数と商品Cの個数の比は3:4 でした。 花子さんは、商品Aを□個、商品Bを□個、商品Cを□個買いました。 (女子学院)
2005.08.20
コメント(0)
-
応用自在算数問題集マラソン(10)
☆☆☆がんばれ小学生!★★★ 応用自在算数問題集マラソン(10)[宿題の解説](1)ポイント:小数と分数は、どちらかにまとめる!ロビンくんは、どうやった?「小数に統一してやってみたら、速かったよ。」7.2 : 13.6 (10倍して)= 72 : 136 (8で割って)= 9 : 17答えは 17(2)単位も、どちらかにまとめる!これも、立方センチメートルに統一しよう。1リットル=1000立方センチメートルだから、0.84リットル=840立方センチメートル840 : □ =14 : 3□ =840×3÷14=180 答え 180★ ★ ☆ ☆ ☆ ☆ ☆ ☆ ★ ★きょうは、応用自在18ページの[11]です。逆比の問題です。わかる!できる!応用自在問題集 算数ロビン、2:3 の逆比は?「3:2 だよ。比が逆になる・・・」そのまんまだけれど、それが逆比です。きみが家から学校を往復するときに、行きと帰りの速さが2:3 なら、かかる時間は3:2になる、というイメージです。逆比の性質をもうひとつ、練習しておきましょう。2つの整数AとBがあって、Aの3倍とBの5倍が等しいときA:Bを最もかんたんな整数の比で表しましょう。ロビン「Aを5とおくと、5×3=15 Bを3とおくと、3×5=15 だから、5:3 」 ほかに、考え方は?ロビン「A×3=B×5 内項=外項 を使って A:B=5:3 」こんな考え方もあるよ。逆数を使う方法・・・。3つ以上の比の場合、逆数を使った方がすっきり解ける。ロビン「逆数は、3の逆数なら1/3 2つかけて、1になればいいんだよね。」その調子。Aの2倍、Bの3倍、Cの5倍が等しいとき、A×2=B×3=C×5=1Aは2の逆数だから 1/2Bは3の逆数だから 1/3Cは5の逆数だから 1/5だからA:B:C=1/2 : 1/3 : 1/52、3、5の最小公倍数は 30 これを右の辺にかけてA:B:C=15:10:6[宿題]( )にあてはまる数を求めなさい。(1)1000円の7割5分は、5000円の( )%です。 (女子聖学院)(2)家から( )mはなれた公園まで時速4kmで歩いていくと、時速9kmで走っていくときより時間は10分多くかかります。(香蘭女学校)おまけ:応用自在P23の[12]も宿題です(^.^)
2005.08.19
コメント(0)
-

応用自在算数問題集マラソン(9)
☆このところ、時間が遅くなっています。良い子のみなさん、ごめんなさいm(__)m夏休みも、残り少なくなってきました。この「応用自在」のコーナーは、夏休みが終わっても続けようと思います。でも、こんなスタイルで、みなさん、分かりますか?☆☆☆がんばれ小学生!★★★ 応用自在算数問題集マラソン(9)[宿題の解説]5000円もっていたら、消費税なしの定価が何円のものまで買うことができますか。ただし、小数点以下は四捨五入します5000÷1.05=4761.9…5001÷1.05=4762.8…4761.9…と 4762.8…との間の整数は4762 です。実際、4762×1.05=5000.1…で四捨五入すれば 5000円! 答え 4762円このように、はさみうちにして求めるのが、四捨五入や切り上げ、切捨ての問題のポイントになります。 ★ ★ ☆ ☆ ☆ ☆ ☆ ☆ ★ ★応用自在18ページの[9]です。わかる!できる!応用自在問題集 算数比の性質の問題ですね。(1) 1.05を分数にしてもいいし、3/5を小数にしてもいいです。 どちらでもできるのが、もっといいです(^.^)(2) 比の値 たとえば、 3:4 なら 比の値は 3/4 この逆に、比の値が 3/4 なら、比は 3:4(3)すなおに「連比」を使って解くのがいいでしょう。――――――――――――――――――――応用自在18ページの[10]もやってしまいましょう。(4)と(5)が間違えそう・・・ロビンなら、(4)はどうする?「48分を秒にかえて、計算かなー?」48分をまるまる計算しない手もあるよ。5の倍数で48に近い数というと・・・「そうか!48分を2つに分けて・・・計算だね。」(5)は、□-2=?という形にもちこめば、いいね。[宿題]次の□の中にあてはまる数を求めなさい。 (1)は山手学院(2)は香蘭女学校の入試問題です。
2005.08.18
コメント(1)
-
応用自在算数問題集マラソン(8)
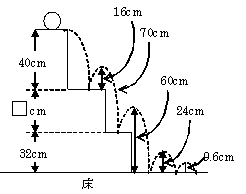
☆親戚の連中とワイワイやっていたら、とんでもない時間になっていました。また、良い子はとっくにお休みの時間になっています(-_-;)明日(正確には今日)は親戚も帰り、再び、規則正しい?日々になります。湘南も、今週一杯で、海辺の賑わいもほぼ終わり、また、静かな季節に戻ります。それにしても、昼は車が大渋滞です。シラス丼をつくろうということになって、近所にシラスを買いに行きました。網本のショップです。裏道を通ってたどり着きました。海岸線も国道1号も何キロという渋滞・・・横須賀の親戚の家に行きたいのですが、今週は諦めました。横須賀に行くと、三崎の新鮮な魚が食べ放題なのです(^.^)早く行きたい・・・☆☆☆がんばれ小学生!★★★ 応用自在算数問題集マラソン(8) [きのうの問題の解説] 床に落ちてからの動きで、跳ね上がる割合がでてきます。 24cm → 9.6cm いま、 24:9.6=5:2=1:2/5 です。 5分の2だけ跳ね上がる、というわけです。すると、ひとつ手前は ( )cm → 24cm ( ):24=5:2 より、 ( )=60cm図に書き入れてみましょう。段の高さ32cmを引いて、60cm-32cm=28cmこれが跳ね上がった高さです。すると、< >:28=5:2 より、< >=70cmこれも、図に書き入れます。はじめに、40cmの高さから落としたら、その2/5の16cm跳ね上がりますね。これも図に書き入れて・・・すると、求める段の高さは70-16=54cm答え 54cm★ ★ ☆ ☆ ☆ ☆ ☆ ☆ ★ ★応用自在の17ページ[8]です。わかる!できる!応用自在問題集 算数消費税の問題が3つあります。(1)(2)は、●×▲=■ですぐに解決します。(3)は実際に、お使いに行ったときに、直面する問題です。でも、今は総額表示なので、計算しなくても済みそうです(^.^)ロビン「消費税の円未満は切り捨てだよね。 消費税なしで900円の品物を買うと、900×(1+0.05)=945円消費税なしで950円の品物を買うと、 950×(1+0.05)=997.5円 だから、997円!」つぎに、ロビンはこんな計算をしました。 ●×▲=■ ●×1.05=1000 ●=1000÷1.05=952.381 ロビン「952円が答えかなー?」952×1.05=999.6円 → 999円 ためしに、 953×1.05=1000.65円 → 1000円 954×1.05=1001.7円 → 1001円 答え 953円☆これがほぼ応用自在の答えに近い考え方です。マックなら ●×▲<■ ●×1.05<1001●×1.05=1001 とおいて●=1001÷1.05=953.…つまり、●<953.…この不等号を満たす最大の整数は953このように考えます。本番のときは、ロビンのようにやる子が多いと思いますが。1000円を5000円にしたら・・・次の問題にチャレンジだよ、ロビン![宿題]5000円もっていたら、消費税なしの定価が何円のものまで買うことができますか。ただし、小数点以下は四捨五入します。(つづく)
2005.08.17
コメント(0)
-
応用自在算数問題集マラソン(7)
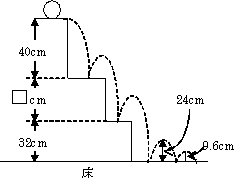
☆☆☆がんばれ小学生!★★★ 応用自在算数問題集マラソン(7)[きのうの問題]ある図書館では、その日の入場者数を前日の120%と予想していましたが、実際は予想していた人数の90%で270人でした。前日の入場者は何人でしたか。[解説]名探偵ホームズのように、現場の状況を見落としのないように調査しましょう(^.^)前日の入場者数を●人とします。魔法のつえ▲は 120%、つまり 1.2 です。魔法の式に登場してもらいます。じゅもんを唱えて、●×▲=■これに当てはめていきます。●×1.2=■このクララ■が、予想していた人数ですね。ところが、この90%しか入場しなかった、というのです。■×0.9=270■=270÷0.9=300こうして●×1.2=300 になりました。●=300÷1.2=250答え 250人ところで、●の120%の90%・・・比の積が使えます。●×(1.2×0.9)=270●×1.08=270●=300÷1.08=250この比の積の問題が、今日のテーマです。★ ★ ☆ ☆ ☆ ☆ ☆ ☆ ★ ★応用自在の17ページ[7]です。わかる!できる!応用自在問題集 算数●の3/5この繰り返しです。1→3/5 1→3/5 1→3/5こんな場合にこそ、比の積を使ってあげます。1回目に跳ね上がる高さは●×3/52回目に跳ね上がる高さは●×3/5×3/5こんな調子で3回目の式を立て、計算すればいいのです。この問題がクリアできたら、P22の[3]にチャレンジしてみましょう。(1) Aからどれだけ落ちて、どれだけ跳ね上がりましたか。 ここが分かれば、跳ね上がる割合が求まります。 たとえば、75cmの高さから落として、50cm跳ね上がったら75:50=3:2=1:2/3こうして、跳ね上がる割合を調べます。BからCは、P17の[7]と同じ問題になります。(2)もP17の[7]の変化形に過ぎません。 次の問題にチャレンジしてみましょう。[問題]あるボールは、落とした高さに対していつも同じ割合ではね上がります。下図のような階段を一番上から点線のようにボールが落ちたとき、一番下の床で1回目は24cmはね上がり、2回目は9.6cmはね上がりました。このとき、2段目の段の高さは何cmですか。(成蹊中学校)つづく
2005.08.16
コメント(0)
-

応用自在算数問題集マラソン(6)
☆☆☆がんばれ小学生!★★★ 応用自在算数問題集マラソン(6)わかる!できる!応用自在問題集 算数[前回の問題の答え]線分図をかいて考えましょう。 まず1日目です。全体を1として、1/2読みました。これを線分図で表すと・・・2日目は残りの2/3を読みました。比の積の登場です。残り1/2の2/3は、1/2×2/3=1/3 です。3日目は12ページ読みました。残りは1/2の1/5です。1/2×1/5=1/10 この後は、2とおりで計算できます。かんたんにやるのなら、線分図から答えは 180ページ です。★ ★ ☆ ☆ ☆ ☆ ☆ ☆ ★ ★さて、きょうの課題は17ページ[6]です。魔法の式●×▲=■ で魔女のモニカ● が1つまり、100%です。これはいつも変わることがありません。ここから、増えたり減ったり・・・これが、魔法のつえ▲になります。●の10%増しなら、 100+10=110%●の20%増しなら、 100+20=120%今回の問題には出てきませんが、●の10%減なら、 100-10=90%●の20%減なら、 100-20=80%これがみーんな魔法のつえ▲です。あとは、●×▲=■にあてはめて、答えを出します。P22の[2]に進んでみましょう。前日の入場者数を●として、さあ、ロビン、その108%とは、何%増しのこと?ロビン「100+8=108 だから、 8%増し!」予想していた人数の95%って、何%減ったの?ロビン「100-5=95 だから、 5%減った!」その調子(^.^)この問題、もうひとつ、比の積で片付けてしまうと早く解けるね。数字を変えて、問題を出してみるよ。[問題]ある図書館では、その日の入場者数を前日の120%と予想していましたが、実際は予想していた人数の90%で270人でした。前日の入場者は何人でしたか。(つづく)
2005.08.15
コメント(0)
-
算数の考え方に強くなる(5)
☆きのうの夜は、親戚の面々と海岸通りの焼肉店に押しかけました。かなりの人が並んでいましたが、予約を取っておいたので、マックたちはすぐに着席&食べられました。海岸にくる人は、浜で遊ぶ前に、予約しておいた方がいいですよ(^.^)☆なかなか本題に入れません。もう少し、さらっと書いた方がいいのかな?とも思います。しかし、話が教育論の方へ行ってしまいがちです。方法論も大切ですが、その基盤となる教育の考え方を明確にしておかないと、せっかくの方法論も、じょうずに使いこなせません。勉強方法は、いろいろあります。しかし、どの方法がいいのかと悩む前に、勉強してどうしたいのか?どういう目的で学びたいのか?どんな人間になりたいのか?答えはすぐには出てこないかもしれません。しかし、こういったことを考えていかないと、勉強に対する気持ちがぐらつきます。そんなわけで、ノウハウよりも姿勢や態度に先に視点がいってしまいます(-_-;)☆算数の考え方に強くなる(5)★「もっとたくさんの穴を、独自の場所で掘ってみる必要がある。そのうちの多くは、たしかに労力の無駄遣いとなるかもしれないが、いくつかはたいへん役立つものとなるはずである。このような穴たくさん掘りはじめるためには、これまで全体を支配してきた大きな穴に対する執着をはっきりと放棄しなければならないだろう。」 (P48)一箇所だけを掘り進めれば、いつかは専門家になれます。こういう方法が、先生や親から推奨されます。いってみれば、リスクの小さい安全な方法です。こどもたちの教育という点にしぼってみると・・・先生や親の立場として、「もっと冒険してみたら?」とは、なかなか言えないものです。こどもに苦労はさせたくない・・・安全で将来を保証された道を歩んでほしい・・・こう考えると、冒険をストップさせてしまう思考方法に傾いてしまいがちです。では、偉人たちの親、とくにお母さんたちはどうでしょう?こどもたちの才能を思いっきりのばすために、世間体や評価を跳ね除け、相手にしません。ひたすら、こどもの才能を開花させることに全力を傾けます。たとえば、発明家のエジソンのお母さんも、学校の評価にこだわりませんでした。そして、こどもを守り、支えるるという点ではだれにも負けませんでした。やがて、エジソンは才能を開花させます。学校の評価では、最低のエジソンでした。その評価は、デボノ博士のいう「ただひとつの穴」、「支配的なアイデア」のもとで下される評価でした。ここまで読んできて、ルソーの「エミール」の思想に似ていることに気がつきました。ルソーも、学校で行なわれている教育に、批判の矢を放ちました。(つづく)
2005.08.15
コメント(0)
-
応用自在算数問題集マラソン(5)
親戚の訪問もピーク・・・早朝から起きてしまいました。きょうの日記も書けたことだし、これで思う存分、遊べます(^.^)☆☆☆がんばれ小学生!★★★ 応用自在算数問題集マラソン(5)[前回の問題の答え]十の位で四捨五入して300になる整数のうち、3の倍数は何個ありますか。ロビン「いっぺんにやっても、混乱しそうだ・・・」ならば、まず300より小さくしていきましょう。290 は 300 になる280 も 300 になる250 までは 300 になる!つぎは、300より大きくしていきましょう。310 は 300 になる320 も 300 になるずっと先に行って350 は 400 になるから300 になるのは 349 まで!ロビン「各位の数字を足して3で割れれば、3の倍数だったから・・・」もっと速く出すには、割ってしまえばいいね(^.^)349÷3=116 あまり 1つまり、1~349に3の倍数は116個249÷3=831~249に3の倍数は83個116-83=33個 答え 33個 わかる!できる!応用自在問題集 算数P17の[5]です。これは、受験生にはおなじみの問題、線分図を描かないと、混乱します。線分図は1本で表すよりも、下へ下へと1日目、2日目、3日目と下ろしていく方が、すなおです。この問題が解けたら、次の問題にチャレンジしましょう。[チャレンジ問題]ある本を読むのに、1日目にその1/2、2日目には残りの2/3、3日目に12ページ読んだところ残っているページ数は1日目に読んだページ数の1/5でした。この本のページ数を求めなさい。(聖和学院中学校)答えは、次回、掲載します。
2005.08.14
コメント(0)
-
算数の考え方に強くなる(4)
☆算数の考え方に強くなる(4)★デボノ博士は、教育、なかでも詰め込み教育を批判します。「教育の目的は、有益だと思われる知識を広く役立てること」教育は垂直思考の世界と言うのです。それに対して、「すでに進んでいる穴を、放棄して、べつな新しい穴を掘り始めることによって、しばしば新しいアイデアや大きな科学的進歩が生まれるのである。」と言います。教育は、古い穴を掘り進めて行く作業なんですね。だから、「それは(筆者注:教育のことです)、伝達的ということはいえても、けっして創造的とはいえない。」かなり厳しく批判しています。つまり、創造性を「教育の場」に求めても、それは無理というもの・・・こういう主張です。たとえで、ファラデーらを挙げています・・・電気の法則に出てきますね・・・彼は正規の教育を受けていませんでした。ダーウィンやマックスウェルも、全面的に教育されなかったから、創造力をふるうことができ、大発見しました。こう書くと、人が人を教育することは、プラスの面ばかりではないという命題が帰結されます。ものごとにはいい面と悪い面がある、表と裏がある、これは教育も同じことなのです。あまり過度に教育されてしまうと、創造力が失われます。芸術の世界が顕著です。たとえば、楽聖モーツァルトに音楽をならっても、彼の影響下にいる限りは、モーツァルトのコピーに過ぎません。もちろん、芸術と科学は違います。芸術には普遍性があり、いいものはいつまでもいいわけです。一方、科学は進歩的です。古い学問は役立たなくなる運命にあります。実際、大学のときに得た知識のままでは、社会に入ってからいずれ通用しなくなります。教育は、科学の知識を教えていくことが主たる目的です。古い穴を掘り進めていきます。しかし、この穴に嵌ってしまうと、今度はそこから出ることがリスクになります。なぜなら、新しく穴を掘って、そこに何もなければ「ムダ」になるからです。自分の地位は、古い穴が基盤です。ここから出て行ったら、地位も失われるかもしれません。なにやら、どこぞの「○政○営化の話」に似ています(^.^)「何かはっきりした結果がでてきてこそ、努力が報いられるもので、その成果が早くでてくるものであればあるほど、努力のしがいがあるといえる。すでに掘り進められた穴をもっと広げることは、実際、将来の発展と成功とを約束してくれる。そして最後に、大きな穴ができあがった時、快適な満足感をうるのである。」(和訳がかなり、直訳っぽいですね。)ある意味、受験勉強そのものです。「将来の発展と成功」が目標になります。「桜咲く」という合格通知は「快適な満足感」そのものです。しかし、他方では、化学オリンピックや哲学オリンピックに日本代表として行っている高校生の子たちもいます。世界の英知が集まる場で、堂々と渡り合うこの子たちは、新しい穴を発見してくれる最有力候補です。そのような青年たちがいるということも、また、事実です。「水平思考の世界」と「教育」とは、本当は互いに補完する・・・マックは、このように捉えています(^.^)脱線しながら、先を続けます。(つづく)
2005.08.13
コメント(0)
-
応用自在算数問題集マラソン(4)
世間は、お盆の休みをとっている方が多いと思います。マックのところにもきょう、明日とそれぞれ親戚がやってきます。静岡や東京都内と近県ですが・・・☆☆☆がんばれ小学生!★★★ 応用自在算数問題集マラソン(4) わかる!できる!応用自在問題集 算数[前回の問題の答え]0.007平方キロメートルの60%は( )平方メートルです。1平方キロメートルは、たても横も1000mの正方形の面積のこと!1000m×1000m=1000000平方メートルロビン「0がいっぱいあって、まちがえそうだよ」そんなときは、1歩ずつしんちょうに進めばいいよ(^.^)0.7平方キロメートルは 700000平方メートル0.07平方キロメートルは 70000平方メートル0.007平方キロメートルは 7000平方メートル用意ができたら ●×▲=■ にあてはめて7000平方メートル×0.6=(4200)平方メートルP17の[4]に入ります。[4] 赤玉も白玉も整数であることに注意しよう。 Aの袋をみてみると、 玉の総数が81個 そのうち、赤玉は30% この0.3は四捨五入したから・・・ 四捨五入する前は、 一番小さくて 0.295 一番大きくて 0.304 の可能性がある。 ●×▲=■ 81×0.295=23.895 以上 81×0.304=24.624 以下 だから、赤玉は24個 <お父様・お母様へ> 自在問題集の解答は、マックにはやや疑問です。 かなり直感的な解答になっています。 お子さんがもし解答を見て悩んだら、とてもできる お子さんです。マックが保証します(^.^) Bの袋も ●×▲=■ 9×0.555=4.995 以上 9×0.564=5.076 以下 よって、赤玉は5個 とするのが、よりよい解答と思います。 ただし、この考え方は、理解がやや困難で、 計算がめんどうくさいという欠点があります。 でも、四捨五入の範囲の計算、入試には必須です。 こどもたち、がんばれ![おまけの問題] 十の位で四捨五入して300になる整数のうち、3の倍数は何個ありますか。 (聖和学院中学校)
2005.08.13
コメント(0)
-
算数の考え方に強くなる(3)
今回はデボノ博士の水平思考の3回目です。話の中で、試験でいい点をとるワクチン法について触れました。参考にしてください(^.^)☆算数の考え方に強くなる(3)★『水平思考の世界』(エドワード・デボノ著、白井實訳)、講談社BLUE BACKS 第3章「古いアイデアの支配」に入ります。冒頭で、博士は改善の方法には2つあると述べます。「一つのものごとを改善するには、それを直接改善する方法と、それを阻害している原因を探り出して、取り除く方法の二つがある。」(P42)成績を上げたければ、いい成績をとっている友だちにノートを見せてもらい、また、勉強方法を教えてもらう・・・これが第一の方法です。逆に、成績がふるわない友だちの勉強方法を観察するというのが第二の方法です(^_^;)その原因がわかれば、彼と同じことをしないように勉強すれば、成績が上がるというのです。いい見本よりも悪い見本の方が、勉強になる?!「失敗学」という学問があります。たとえば、大企業でも、つぶれる企業があります。なぜそうなったのか、その原因を探り、同じ過ちを事前に避ける・・・そんなことを研究する学問です。これをやると失敗する、そういう原則があります。算数なら、割合と比、そして整数の特別な性質を理解しないで分数に入ると、分数が分からない状態になります。順序立てて進めればいいのですが、分数計算が先に入ってきます。こどもたちにとっては、割合や比に入るまで、苦しい季節が続きます。また、勉強時間が多いから、成績がいいという関係は時として成り立ちません。ポイントのずれている勉強をいくらしても、成績は上がりません。このスタイルは、まじめな子に多いといえます。たしかめ算をしない子は、つまらないところで点を落とします。こういうつまらないミスをして、泣く子がたくさんいます。算数や数学でいい成績を取るための方法のひとつをそっと教えます。それは ・ ・ ・ワクチンを打っておく!ということです(^_^;)ふだんの勉強で、ミスを誘導するようないじわる問題・・・たいていは、入試問題がそうです(^.^)・・・に数多くあたっておくのです。これがワクチンになります。本番でミスをしない予防薬になってくれます。素直な問題だけ解いているだけでは、本番でワナにはまります。温室育ちではダメ! ということです。素直なだけじゃ、いい子でおしまい・・・たとえば、車の運転の場合、どんな条件でも、ベテランは切り抜けます。体にワクチンができているからです。事故が起こりそうな状況を事前に読めるので、自然に注意力が高まります。さて、デボノ博士のアイデア創出法も、アイデアをつぎつぎと生み出す人のマネをしようとする方法と、アイデアが出てこない人をじっくり観察する方法の2つがあるというのです。「ある人がどうして発明できたかを調べる代わりに、他の人にはどうして発明できないのかを調べた方が意味がある。新しいアイデアを生み出す場合にも、一般の人々、ある種の人々になぜアイデアが生まれないのかを見通すことができれば、新しいアイデアを生み出す能力を育てることができるかもしれない。」(P42)一言で言えば、失敗例に学べ! ということですね(^.^)(つづく)
2005.08.12
コメント(0)
-
応用自在算数問題集マラソン(3)
☆☆☆がんばれ小学生!★★★ 応用自在算数問題集マラソン(3) わかる!できる!応用自在問題集 算数[前回の問題]1500円は( )円の125%です。125%は1.25のこと。森の計算機で100%をめもり1にして、125%を計算すると出てくるね(^.^)慣れると、頭の中で計算できるよ。●×▲=■にあてはめて( )円×1.25=1500円( )円=1500円÷1.25=1200円答えは 1200円計算ミスを防ぐために、すぐに「たしかめ算」をしておきましょう。1200円×1.25=1500円OKですね(^.^)では、P16の[3]に進みます。[3](1) 定員が100人としたら、その140%は何人? ●×▲=■ にあてはめて、 100人×1.4=( )人 これが出れば、あとは分かるね(^.^)(2) 330人は●か■かどちらかだよ。 きみはどっちだと思う? この問題は、これが山場! (3) 半分の半分て、どう考える? ヨウカン1本持ってきて、分けてみよう。 ヨウカン1本を半分にして、 半分になったヨウカンをまた半分にすると、 4分の1 になったね。 どんな計算がかくれているのかな? 0.5×0.5=0.25 1/2×1/2=1/4 比と比はかけ算ができる。比の積だね。 それじゃ、別にヨウカンをもう1本持ってきて、 はじめに3等分、2回目に3等分したうちの1本を 2等分したら、それはもとのヨウカンの( )分の1になる。 かけ算をしてみよう。 1/3×1/2=1/6 だから、6分の1になったんだね(^.^) もちろん、2回に分けてもいいね。 後ろから計算して、 まず、女子の人数を出し、 それから、全生徒の人数を出してもいいよ。 でも、これから先の問題で、比の積を利用した方が 答えは速攻で出てくるから、ヨウカンのイメージを 繰り返しておこうね。 [おまけの問題] 0.007平方キロメートルの60%は ( )平方メートルです。 (十文字中学校)
2005.08.12
コメント(0)
-
算数を実験してみよう(3)
☆きょうもひたすら暑いですねー。湘南地方は小雨が降ったので、いま、涼しい風が吹きはじめました。暑さに負けず、きょうも算数ラボを始めます(^_^;)□■□■□■□■□■□■□■□■□■□■□■算数を実験してみよう(3) [前回の問題の解説]100m競争でスタートラインが違う! そんなイメージの問題です。Aさんがちょうど真ん中まできたとき、BさんはW駅につきました。歩く速さは同じ。ということは、きょりも同じです。Aさんのちょうど真ん中、BさんはW駅、ここをスタートラインにしましょう。同じきょりは・・・ “カット”して考えましょう。複雑系からシンプル系へと、向かうのです(^.^)これが問題を解くときの テクニック です。この時点で、Aさんは900m得をしています。でも、Bさんは電車に乗る分早くつきます。ところで、BさんはAさんがスタートしてから1分後にスタートし、6分早くつきました。ということは・・・差に注目します。もしもいっしょにスタートしていたら、Bさんは、Aさんより7分早くついていたことになりますね。電車は時速30kmです。分速になおすと30000m÷60分=500m「7分早くついた」をきょりにかん算すると500m×7分=3500mここで、ふたたび、差に注目!!!Bさんは900mの差をつけられていました。でも、T駅についたときには、3500mの差をつけていました。合計で、4400mの差をつけた・・・このように考えられます。1分間で2人のきょりは500m-60m=440mずつ差がつきす。魔法の式よ、出でよ!●×▲=■●は 440m■は 4400m440m×▲分=4400m▲分=10分スタートラインと考えた地点から10分後、AくんはT駅につきます。●×▲=■60m×10分=600mこの地点はちょうど真ん中でした。なので、Aくんはこの倍のきょりを歩いたのです(^.^)答え 1200m☆ダイヤグラムで表すと、話はかんたんになります。ビジュアルに考えやすくなります。力のある子は、真ん中の地点からのダイヤグラムをつくって、実験してみましょう。☆こういう変則ダイヤグラムで考える、という問題が出てくるのが入試です。だから、ダイヤグラムの意味をしっかりと理解することが大切なんですね(^.^)※きょうは宿題はありません。
2005.08.12
コメント(0)
-
応用自在算数問題集マラソン(2)
日刊の発行めざしていますが、時間が遅くなってしまいました。良い子はもうお休みの時間ですね(^_^;)☆☆☆がんばれ小学生!★★★ 応用自在算数問題集マラソン(2) わかる!できる!応用自在問題集 算数P16の[2]です。百分率の問題です。魔法の式●×▲=■をイメージして解いていきます。ロビンはノートに書き出しました。● もとにする量▲ 割合■ くらべられる量マックは黒板に書き出しました。● 魔女のモニカ▲ 魔法の杖■ クララマック:名前をくらべてみよう。ロビン:なんか、似ているね。覚えたら、つぎは、割合の表し方。「きみは100%の力を出しきったか?」ドラゴン桜に出てきそうなセリフです。この100%は「すべて」「全部」「もと」ということ。もとにする量●が100%だよ。数直線で1のところ・・・ここが100%(1) kgとgの単位を合わせよう。 小数点を使いたくないなら、gに統一しよう。(2) 1時間は何分だっけ? 時間を求めるから、24分を時間に直した方が速そう。(3) たても横も100cm(1m)の正方形の面積が1平方m(4) まず、前半からかたづけて、それから後半に移る。 むずかしそうに見えても、バラバラにすれば簡単になる例 だね(^.^) 1割を小数で表すと・・・(5) これも、前半→後半 で2つに分けて計算しよう。 1割1分を小数で表すと・・・ 野球をイメージしてみよう。 どんなにうまいバッターでも、3割台を打つのはかなりハード。 3割っていうと、10回打席に立って、ヒットが3回ということ。 10回打席3安打 10分の3 0.3 このイメージで、数を変化させることに慣れようね。 [おまけの問題] ※答えは次回に掲載します。 1500円は( )円の125%です。 (相模女子大中等部)(つづく)
2005.08.11
コメント(0)
-

算数を実験してみよう(2)
問題によっては、線分図で表すのが難しい場合があります。そんなときは、表であらわせないかな? と一歩先へ進みます。表はつくり慣れないと、線分図よりもむずかしいかもしれません。でも、理科や社会では、たくさん表が出てきます。教科書の表を自分でつくり直すと、表の性質が分かってきます。表の中でも、今回の問題のように状態を表すだけというのは、比較的、手がつけやすい問題です(^.^)□■□■□■□■□■□■□■□■□■□■□■算数を実験してみよう(2) [前回の問題の解説]A、B、C、Dの4つの電球で、明かりがついているときを○、消えているときを×としましょう。そして、2秒間ついていれば ○○ などと表します。すると、A、B、C、DはそれぞれA ○×○× ○×○× ○×○× ○×○×B ○○×× ○○×× ○○×× ○○××C ○○○○ ×××× ○○○○ ××××D ○○○○ ○○○○ ×××× ××××になります。目がチカチカしてきますが・・・(1)スイッチを入れてから、最初に4つの電球の明かりが同時に消えて いるのは何秒後から何秒後の間ですか。 はじめに、全部の明かりがついているのは、0~1秒後です。 表を見ていくと、最後のところで全部消えています。 答え 15秒後から16秒後(2)電球の明かりが2個だけついているのは、スイッチを入れてから 1分間に合計で何秒ありますか。 0~16秒後では、6秒間ありますね。 16~32秒後も、6秒間。 32~48秒後も、6秒間。 つぎからは、数え上げです。 51~52秒後 そして 53~54秒後、54~55秒後、57~58秒後、58~59秒後でおのおの1秒間、 合計すると、 6×3+5=23 答え 23秒次も、学習院女子の問題です。[問題]学校からT駅へ行くのに、直接歩いていく行き方と、W駅まで歩いてから電車に乗っていく行き方があります。道のりは直接歩いていく方が900m短いです。いまAさんとBさんが同時に学校を出発し、Aさんは毎分60mの速さでT駅に直接向かいました。Bさんは毎分60mの速さでW駅に向かい、Aさんがちょうど半分まで来たところでW駅につきました。1分間電車を待ってから乗ったところ、Aさんより6分早くT駅につきました。電車は時速30kmです。Aさんが学校からT駅まで歩いた道のりを求めなさい。 (学習院女子中等科)
2005.08.11
コメント(0)
-
算数の考え方に強くなる(2)
☆算数の考え方に強くなる(2)★『水平思考の世界』(エドワード・デボノ著、白井實訳)、講談社BLUE BACKS 第2章「アイデアを生み出す法」をもう少し続けます。新しいアイデアは、そうそう簡単に生まれてくるものではありません。「新しいアイデアを実用化する技術が、長い間すでに存在していても、アイデアはまったく散発的にしか生まれてこない」(P38)なにかアイデアは出てこないかと、いろいろなノウハウを使ってみます。たいていは、3日坊主で終わります。既にあるものを解釈しなおせばいい、並べ換えればいいと言われて試みます。しかし、何も見えてきません・・・新しいアイデアを発展させるというのは、日本人の得意とするところです。しかし、そのスタートになるアイデアとなると、「アメリカにいいアイデアがある」ということで、アメリカに学びにいきます。これは、江戸時代の末に福沢諭吉一行が咸臨丸でアメリカに行った頃とほとんど変わっていません。アイデアはどうしたら生み出せるのか? この章末でデボノ博士は一つの命題を出しています。「発明家や有名な科学者たちは、いつも一つだけではなく、一連の新しいアイデアを生んでいる。」つまり、アイデアを出す人は、たくさんのアイデアを多産するというのです。偏りがあるということです。「これは、新しいアイデアを生み出す能力には、人によって程度の違いがあることを示している。」アイデアを出すような頭の構造(考え方)があるといっています。「この能力は、すべて知能に関連しているというより、特定の思考習慣、特定の思考様式に関連があるように思われる。」考え方、ものの見方を変えればアイデアが出てくるようになる!希望が出てきました。成績や知能ではなく、どうやら考え方のスタイルが、アイデアの創生に重要な関係があるのですから。(つづく)
2005.08.11
コメント(1)
-
応用自在算数問題集マラソン(1)
☆☆☆がんばれ小学生!★★★応用自在算数問題集マラソン(1) 今回から、「応用自在算数問題集」を使ってこの問題集の問題を制覇(せいは)していきます。わかる!できる!応用自在問題集 算数問題集を持っているけれど、答えを見ても???のロビンといっしょに進めます。ロビンがこの物語の主役です。ロビンは、マックが以前教えたことのあるフランス人の子がモデルです(^.^)日本語は話せるけれど、字が分からないというKくんでした。レッスンは、共通語の英語でやりました。それはそれは、お互いにとってとてもやりにくい状況でした。Kくんのお母様は日本人で、私の先輩のお姉様。日本の学校に入れたいということで、特訓しました(^.^)このKくんに算数基礎から説明し直しました。応用自在を使ってでしたが、フランスの学校の教え方と当然異なります。引き算はアメリカ式、分数も1/3を3分の1とは読みません。九九もありません。漢字の勉強と併行して、算数と数学、理科の勉強をやりました。このKくん、台風の日に海に出かけて泳ぐといういたずらん坊でした。いろいろなエピソードが残っています。フランス語は当然きれいで、マックの娘たちが「話して」とおねだりすると、フランス語で詩を暗唱してくれました。哲学はよく知っていました。学校の授業で、こういう勉強をするというのは、日本と土壌が異なります。たぶん、フランスの人にとって、哲学は日常生活の一部なのでしょう。日本の学校でいう「考える」ということに、とても近いと思いました。ものごとを分析したり、統合したりして、論理的に話を進めていくのが特別なことではないのです。もうひとつ、強く感じたのが、受けられる教育レベルの差が、とても大きいということです。社会層が固定しているので、ハイクラスに属するこどもたちは、質のよい教育を受けられます。しかし、それ以外のこどもたちは・・・たいていはチャンスがありません。そこで国外に行くという選択肢を採ることになります。さて、ロビンくん、応用自在問題集をどこまでやり切れるか?第1回目は、P16の<数量関係>からスタートします。[1]からです。単位の計算問題です。ヒントを出します。[1](1)重さはキロ(k)がつくから、1000倍の世界(2)面積は、正方形をイメージして 長さを10倍ずつしていきます。 スタートは1辺が1mの正方形。(3)牛乳パックやペットボトルをイメージします。 1リットルの1000分の1が、1ミリリットル、 この1ミリリットルが1立方cmです。(4)デシ(d)は10分の1・・・ 1リットルの10の1が1デシリットル キロ(k)は1000倍・・・ 1リットルの1000倍が1デシリットル(5)時間は60進法ですね(^.^) 1時間→60分→3600秒 これを「森の計算機」に書き込み、 計算していきます。(6)あまりの12秒がおジャマムシです。 32÷5=6・・・2 ならば、 (32-2)÷5=6 ですね。 これと同じように、あまりから処理していきます。 こんな感じで毎日1問ずつ進めて行きます。スピードはゆっくりですが、着実に進んでいきましょうね。ところで、このブログを読んでいただいているきみだけに、「森の計算機」を紹介しておきます。フリーページのどこかに、隠れています(^.^)
2005.08.10
コメント(0)
-

算数を実験してみよう(1)
☆気がついたら、カウンターが1万アクセスを超えていました。楽天日記スタートからほぼ2年間、3分の2はお休みしていましたが(^_^;)今回から、「算数で実験」コーナーをスタートします。中身は変わり映えしない可能性もありますが・・・算数は、紙の上で気軽に実験できます。その書くという作業が、ひらめきにつながります。レオナルド・ダ・ビンチはメモを大量に残しました。なんでもメモしていたのですね。このメモする習慣がアイデア、自分だけの発想力をつけてくれます。こんなことを頭の片隅において、問題をいっしょに解いていきましょう(^.^)□■□■□■□■□■□■□■□■□■□■□■算数を実験してみよう(1) 図のようにA、B、C、Dの4つの電球があります。スイッチを入れると4つの電球の明かりが同時につき、その後Aは1秒ごとに、Bは2秒ごとに、Cは4秒ごとに、Dは8秒ごとに明かりがついたり消えたりします。例えば、Dは8秒間明かりがつき、次の8秒間明かりが消えます。(1)スイッチを入れてから、最初に4つの電球の明かりが同時に消えて いるのは何秒後から何秒後の間ですか。(2)電球の明かりが2個だけついているのは、スイッチを入れてから 1分間に合計で何秒ありますか。 (学習院女子中等科)(つづく)
2005.08.10
コメント(0)
-
算数の考え方に強くなる(1)
☆算数の考え方に強くなる(1)★『水平思考の世界』(エドワード・デボノ著、白井實訳)、講談社BLUE BACKS を読み返しています。「アイデアを生み出す法」という章があります。「新しい情報は、確かに新しいアイデアを生み出せるが、かりに新しい情報がなくても、新しいアイデアを生み出すことはできる。それには、あらゆる古い情報を検討し直して、それらをきわめて有効な新しい方法で一つにまとめればよい。」(引用)最先端の知識や技術に触れていないと、画期的なアイデアが出てこないと諦めるのは早い!ということです。アイデアを生み出すチャンスは誰にでもあるということです。その例としてアインシュタインが紹介されています。「そのもっともよい例は、アインシュタインだろう。彼は何ひとつ実験もせず、新しい情報も集めずに、新しい相対性理論を考え出している。何一つ実験をしなかったのだから、いいかえると誰でも入手できる情報に新しい見方を与えたにすぎない。むしろ相対性理論を裏づける実験は、後になって行なわれている。」(引用)それまで常識だったニュートン力学に一石を投じました。そして根本から、ひっくり返してしまいました。もとになる情報は同じです。常識的な見方を変えただけです。これが、革命的な変化を物理の世界にもたらしました。アイデアは、ものの見方をほんのちょっと変えればいい!それで、新しいアイデアが生み出される、というのです。この考え方は素敵です。誰もが、偉大な発見者、発明家になる可能性があります。逆に、これまでの理論や体系化された知識から離れられないと、アイデアは生まれてこないと、デボノ博士は警告しています。算数の公式も、そういった面があります。デボノ博士は実験をして、公式の有用性と限界を示しています。第3章 古いアイデアと新しいアイデア でその実例が示されることになります。(つづく)
2005.08.10
コメント(0)
-
数の動きって? その46(再)
☆親戚の面々とおしゃべりやら海水浴やらで、騒々しかった休みが終わりました(^.^)日記の更新もままならず、失礼いたしましたm(__)mやっと正常な日々が戻りつつあります。きのうは、その間隙を抜けて、早朝、歴史的建造物の清掃作業に参加してきました。坂道を熊手で掃いていたのですが、腰にきました(-_-;)きょうは、これから家の周囲の草刈りです。藪蚊とのバトルをやってきます・・・■数の動きって? その46[宿題]青陵博物館の入館料は、大人料金が子ども料金よりも100円高くなっています。この博物館に大人5人、子ども5人で入館するときの入館料の合計と、大人6人、子ども5人で入館するときの入館料の合計の1割引きは同じでした。このとき、割引き前の大人料金を求めなさい。[解説]比に注目します。大人料金と子ども料金の比です。大人は5人から6人に増えています。1割引きの6人の料金は、割引き前の5.4人分です。子どもは人数は変わりません。料金は割引き前の4.5人分になっているはず・・・大人が0.4人分料金が増え、子どもは0.5人分料金が減り、全体としては料金は同じです。大人料金と子ども料金の比が出てきました!大人0.4人分と子ども0.5人は、同じです。比は、0.5:0.4小数でわかりにくければ、10倍して(大人料金):(子ども料金)=5:4この差が100円でした。5:4=500:400これで解決!答え 500円☆応用自在問題集をやっている方はいますか?次回から、ランダムに解説していきます。リクエストがあれば、掲示板などでお知らせください(^.^)
2005.08.08
コメント(1)
-
数の動きって? その46
☆親戚が泊まりに来ています。海が近いもので、親戚が泊りがけでやってくるのです。しかし、8月に入ると、鵠沼の海は電気クラゲが出始めるので、気をつけないと刺されます。ときどき、救急車でサーファーが運ばれていきます(-_-;)浜辺の近くにも、波に乗って移動してくるので、鵠沼の住民は、泳ぐために海に行く事は、ほとんどありません。でも、親戚が来たときは別。プールでは納得してくれません。それで、いっしょに海に行くのですが、電気クラゲにやられないように、周囲をキョロキョロしなければなりません。変な人に間違われそうです・・・浜辺には、小さなクラゲが漂着して、浜にへばりついているのを、ときどき見かけます。半透明で、きれいですよ。ところで、電気クラゲは、正式には「カツオノエボシ」といって、日本の海ならどこにでもいます。刺されたら、気絶するほど痛いそうです。8月の海は、危険な香りがします(^.^)■数の動きって? その46[宿題]青陵博物館の入館料は、大人料金が子ども料金よりも100円高くなっています。この博物館に大人5人、子ども5人で入館するときの入館料の合計と、大人6人、子ども5人で入館するときの入館料の合計の1割引きは同じでした。このとき、割引き前の大人料金を求めなさい。答えを書こうとしたら、親戚がやってきました。また後ほど書きます・・・m(__)m
2005.08.06
コメント(1)
-
数の動きって? その45
☆中学生の子たちに英文日記の補講をしています。いまどきのこどもたちは、人前で○○になりたい!ということを言いたがりません。とてもクールになっています。夢と現実が違うということが、いろいろな情報経路から入っているのです。夢をこわすような伝達の仕方で情報が入ってくると彼らは冷めた眼差しで世の中を見がちになります。いいことも悪いことも両方をきちんと教えてあげることが必要です。インフォームド・コンセントです。しかし、情報は一方的に入ってきます。判断力がまだ充分でないこどもたちには、情報の真価がわかりません。しかし、場の空気で情報に反応してしまいます。そして、入ってくる情報はマイナスの情報が多いのが現状です。ニュースやマスコミでは、宇宙飛行や陸上競技の話などの明るい話題もあります。しかし、事件が多すぎます。未来に希望をもつことのできる情報がたくさん入ってこなければ、夢は育ちません。自分たちの将来像も描けません。一方、こうなりたいという模範(モデル)がない時代、主役不在の時代といえるのかもしれません。豊かな時代に育つこどもたちです。あくせくするなんていうことは、原始時代の考え方のように受け取られがち・・・そこそこ生きていける、という思考をしています。ほんとうは、現実ってそんな生易しくはないのですが、そういう過酷な現実に直面する経験をすることは、たいていの子にはありません。でも、これから何年か後に、社会に出て行く彼らに必要なのは夢であり、希望です。「自分の会社、ショップを持つとしたら、どう?」こう振ってみました。最初はもたつきました。・好きなことは何?・自分に向いていることは何?・きみの個性って何?質問をしていくと、だんだん話が出始めるようになりました。・すぐに、現実的かどうかは判断しないこと・成功する人たちは、どういう特質をもっているか?質問を交え、こどもたちの心の中を掘り下げていきます。「具体的な未来が描けなければ、努力することができません。 辛抱することもできません。」こどもたちを取り巻く環境は恵まれているようで、実はその内容は貧しい、そう思えることもたくさんあります。さらに、少子化や高齢化で、この日本は未体験ゾーンに突入していきます。そういう波を乗り越えていく力を身につけていくことがこどもたちにとって大切なことなのです。■数の動きって? その45[宿題]ビデオデッキで、あるテープに録画するとき、標準モードでは2時間、3倍モードでは6時間、それぞれ録画することができます。4時間20分のテレビ番組をこのテープにぴったり録画する場合に、標準モードで録画しはじめると、途中から3倍モードに切りかわります。3倍モードに切りかわるのは、標準モードで録画しはじめてから何分後ですか。 西部学園文理中学校※つるかめ算で解く方法で解説します。全体の量も1で表します。1は100%で、全体を表すというテクニックは算数でよく使われます。この表し方、ほんとうは、こどもたちにとって、かなりの負担になります。不親切といってもいいでしょう。分数の世界に入っていくので、計算もたいへんです(-_-;)だからマックの塾では、別のやり方でやっています。慣れてきたら、1でやってもらいます(^.^)[宿題の答え]迷ったら、「魔法の式よ、出でよ!」●×▲=■はい、出てきました。全体の量■を1としましょう。標準モードなら2時間かかる・・・少女クララ▲が2です。●×2時間=1●=1/2時間3倍モードなら6時間かかる・・・●×6時間=1●=1/6時間単位あたりの量●は、速さを表していますね。ここからが、つるかめ算になります。もしも、もしも、・・・標準モードで4時間20分撮ってしまったら、・・・この「もしも」で、スタートします。4時間20分は、13/3時間です。速さ×時間の感覚です。1/2×13/3=13/6テープは1しかありません。13/6では、13/6-1=7/6 もオーバーしています。この原因、わかりますね。「もしも」がワルサをしているのです。1/2 を 1/6 に変えないと、ダメです。1/2 - 1/6=1/3この差の1/3があるから、7/6もオーバーしているのです。7/6÷1/3=7/2時間3倍モードは7/2時間必要ということがわかりました。全体で13/3時間でした。13/3 - 7/2 = 5/6時間つまり、50分答え 標準モードで50分[宿題]青陵博物館の入館料は、大人料金が子ども料金よりも100円高くなっています。この博物館に大人5人、子ども5人で入館するときの入館料の合計と、大人6人、子ども5人で入館するときの入館料の合計の1割引きは同じでした。このとき、割引き前の大人料金を求めなさい。 青陵中学校(つづく)
2005.08.05
コメント(1)
-

数の動きって? その44
☆問題の基礎力を磨くという意味で、応用自在問題集「算数」から話題を拾っていこうかと思います。わかる!できる!応用自在問題集 算数この問題を題材に、どういうアプローチをしていけば算数の力がつくのか・・・その基本の部分についてプログでどう展開できるか、実験していきます(^.^)■数の動きって? その44[前回の宿題]3つの品物A、B、Cがあります。A1個の値段はB1個の値段の7割5分に等しく、C1個の値段はA1個の値段の20%増しです。また、Aの品物2個とBの品物3個とCの品物5個の合計の値段は1800円となります。このとき、次の問いに答えなさい。(1) A1個とB1個の値段を最もかんたんな整数の比で表しなさい。(2) A1個とC1個の値段を最もかんたんな整数の比で表しなさい。(3) A1個の値段はいくらですか。 成城学園中学校[解説]順番に解いていけば、すぐに解答が終わってしまう、とても親切な問題です(^.^)(1) このままでわかってしまう子はOKです。 迷ったら、魔法の式を使います。 ●×▲=■ B×0.75=A A:B=(B×0.75):B =3/4:1=3:4 答え 3:4(2) 魔法の式よ、出でよ! ●×▲=■ A×(1+0.2)=C A:C=A:A×(1+0.2)=1:1.2=10:12=5:6 答え 5:6(3) ここからは連比になります。 A : B : C 3 : 4 5 : 6 ──────── 15 : 20 : 18 そこで、A1個の値段を15円、B1個の値段を20円、 C1個の値段を18円と、かりにおいてみます。 合計の金額は 15円×2個+20円×3個+18円×5個 =30+60+90 =180円 実際の金額は 1800円 なので、 かりの値段を10倍してあげればいいのですね。 答え 1800円いまどき、ビデオデッキは減って、こどもたちの中には知らない子がいるかもしれません。でも、入試には出てきます。いろいろなことを見たり体験したりする子の方が強い!!!このことは、入試にもあてはまります(^.^)[宿題]ビデオデッキで、あるテープに録画するとき、標準モードでは2時間、3倍モードでは6時間、それぞれ録画することができます。4時間20分のテレビ番組をこのテープにぴったり録画する場合に、標準モードで録画しはじめると、途中から3倍モードに切りかわります。3倍モードに切りかわるのは、標準モードで録画しはじめてから何分後ですか。 西部学園文理中学校(つづく)
2005.08.04
コメント(1)
-
Rくん、剰余系を使う(15)
☆剰余系のお話、今回が最終回です。剰余系の体系化には、ドイツの数学者ガウスなども携わっています。また、素数の話、整数論の話も剰余系の性質をうまく使うことで、いろいろと展開していくことができます。この日記で、剰余系をまた扱うことがあるかもしれません。中学入試に、この分野の問題がときどき出てきますから・・・それでは最終回にいきます。■■■ Rくん、剰余系を使う(15) □□□□[宿題]次の( ア )と( イ )にあてはまる数を求めなさい。4,5,6のどれで割っても2余る2けたの整数( ア )と、2,3,4のどれで割っても1余る整数( イ )の和は111になります。 鎌倉女学院中学校(改題)[考え方]この問題もシンプルです。( ア )≡2 (mod4)( ア )≡2 (mod5)( ア )≡2 (mod6)(( ア )-2)≡0 (mod4)(( ア )-2)≡0 (mod5)(( ア )-2)≡0 (mod6)つまり、( ア )-2 は、4、5、6のどれで割っても割り切れます。4、5、6の最小公倍数は60なので、( ア )-2=60( ア )=622,3,4の方は、最小公倍数は12( イ )-1=12,24,36,48,60,・・・・( イ )=13,25,37,49,61,・・・( ア )+( イ )=111 となるような組み合わせはアが62、イが49 しかありません。 ・・・答え☆次回から、『Rくん、中学数学ベーシック』を連載します。それで、このコーナーはテーマが<中学生の勉強>になります。さて、どんな内容にするか? これから考えます(^.^)魔法の式 ●×▲=■ がベースです。中学数学にチャレンジしていきます。こんな内容がいい! という希望があれば、掲示板に書いていただけると、うれしいです(^.^)
2005.08.03
コメント(1)
-
数の動きって? その43
☆江の島花火大会 きょうの夜は空けています。なんといっても花火大会です。お祭りが好きなマックとしては、血が騒ぎます(^.^)下の娘サーヤは浴衣姿で出かけていきました。上の娘カオリンは受験勉強のため、家でがんばると言っています。しかし、ロフトから花火が見えます(^.^)多分、スイカを食べながら、見ることになるでしょう。私たち夫婦は・・・散歩がてら夜の浜辺に出かけてきます。■数の動きって? その43[前回の宿題]A国、B国、C国の人口の比は30:25:2で1平方キロメートル当たりの人口はそれぞれ二千人、一万人、五百人です。A国、B国、C国の面積の比を最も簡単な整数の比で表すと、□:□:□です。[宿題の解説]比の商の問題ですね。魔法の式●×▲=■を使えば、答えが自然に見えてきます(^.^)面積の比を ア:イ:ウ としましょう。●×▲=■にあてはめて、A国 二千人×ア=30B国 一万人×イ=25C国 五百人×ウ=2二千人、一万人、五百人を簡単な比で表すと2000:10000:500=20:100:5=4:20:1すると、この比を使うことでA国 4×ア=30B国 20×イ=25C国 1×ウ=2と簡単になります。ア:イ:ウ=30/4:25/20:2 =30/4:5/4:8/4 =30:5:8答え 30:5:8混乱しそうになったら、魔法の式!●×▲=■を紙に書いて、机の前に貼っておきましょう(^.^)比の問題を続けましょう。[宿題]3つの品物A、B、Cがあります。A1個の値段はB1個の値段の7割5分に等しく、C1個の値段はA1個の値段の20%増しです。また、Aの品物2個とBの品物3個とCの品物5個の合計の値段は1800円となります。このとき、次の問いに答えなさい。(1) A1個とB1個の値段を最もかんたんな整数の比で表しなさい。(2) A1個とC1個の値段を最もかんたんな整数の比で表しなさい。(3) A1個の値段はいくらですか。 成城学園中学校(つづく)
2005.08.02
コメント(1)
-
Rくん、剰余系を使う(14)
☆親戚が来ているので、いろいろと話が盛り上がり、な、なんと、午前0時を回っています(-_-;)きょうは中学生の子たちと、未来日記をつくりました。ただし、日本語ではなく、英語で書いていくというもので、学校の宿題でもあるのです。常備してある「13歳のハローワーク」をみんなで眺め、将来のシナリオをほぼ3年間隔でつくる作業です。でも、まだ分からないこと、未確定なことが多過ぎて、みんな苦労していました。こどもたちは、それぞれ個性があります。表現するのが好きな子は活発です。じっとして講義を聴くというスタイルよりも、参加型の講義を好みます。自分で体験しないと納得しないタイプです。組織の中では、うるさがれる可能性もあります。学校で優秀な成績をとる子に多いのが、調整型の性格の子です。みんなをまとめていくのが上手です。意見は中庸で、ときに自分を抑えてしまうこともあります。系統だって分析するのが好きなので、組織の中で重宝な存在です。上役が使いやすいタイプでもあるのです。学校の先生方にも、好かれるタイプの子です。どちらかというと、ひとりでこつこつと研究していくのが好きな性格の子もいます。発明家タイプです。表現型の子と反対に、ふだんは静かな環境を好みます。しかし、アイデアが閃くと、とても行動的になります。組織の中では、扱いにくいとみなされてしまうおそれもあります。一貫して静かな雰囲気を好むのが、哲学者タイプの子です。考え方もしっかりしています。じっくり、ものごとに取り組んでいきます。組織の中では、スローテンポがマイナスに受け取られる可能性があります。しかし、話をするととても刺激的な思考方法をしているので、研究者として大成する可能性が高いといえます。このほかにも、いろいろなタイプの子がいます。そして、たいての子は、2つか3つのタイプを合わせ持っています。どのタイプが優勢かで、こどもに対する教え方も違ってきます。将来の職業も、こどもたちの個性を明らかにして、それからいっしょに考えてあげる・・・ほんとうはこういう作業が必要なのだと思います。今の日本、自分の個性がわからないまま職業を選ぶというミスマッチが起こっています。学習の仕方でも、同じ現象が起きています。講義でも話で終始するスタイルの講義、動きをとり入れて、参加型のスタイルをとる講義、ビジュアルに展開し、イメージを多用する講義など・・・こどもたちの個性にあわせ、才能を引き出すことができるように、いろいろな実験が行われていくべきと思ったりしています。ほんとうは、一人一人のこどもたちに合った講義を行うのが理想です。個性を見つけてあげる・・・学習でも、将来の職業の選択でも、この個性が分からなければ、ミスマッチが起こります・・・■■■ Rくん、剰余系を使う(14) □□□□[前回の宿題]38を割っても、54を割っても6余る整数をすべて求めなさい。 明治大学付属中野中学校[考え方] 割る数をAとおきましょう。 38≡6 (modA) 54≡6 (modA) 割り切れる形に変えましょう。32≡0 (modA)48≡0 (modA 32と48の公約数は・・・ 2×2×2×2 が最大公約数 2のファミリーしかありません。 1,2,4,8,16 になります。 でも、最後のつめで、あわてると・・・ このうち、6より大きくないと、余りの6が出てきません(^.^) 答えは 8,16 [宿題]次の( ア )と( イ )にあてはまる数を求めなさい。4,5,6のどれで割っても2余る2けたの整数( ア )と、2,3,4のどれで割っても1余る整数( イ )の和は111になります。 鎌倉女学院中学校(改題)(つづく)
2005.08.01
コメント(0)
-
数の動きって? その42
☆親戚が来たり、先輩の家に行ったりで、1日がたちまち過ぎてしまいました。塾のこどもたちも、ご両親の実家に行く子がいたり、旅行にいく子がいたりで、スケジュールが変則的です。スケジュールを立てるのも、1対1対応の問題なのですが、体が2つほしいところです(-_-;)■数の動きって? その42[前回の問題の解説と答え][1]と同じ規則で・・・とあるので、[1]をよーく見てみましょう。たても横もななめも、ドレを取ってもみーんな15になっています。1~9までの数の和は、45各列(各行)とも和が同じなので45÷3=15各列(各行)とも、和は15になります(^.^)もうふたつ、ウルトラ大切なことがあります。これを見落とすと、ゴールまでの道のりは果てしなく遠くなります。何でしょう?ひとつめは ま ん な かど真ん中の数が、5この5は1~9までの数の平均です。この5が真ん中に入っています。[2]の真ん中の数と比べてみましょう。[2]は、1~25の整数で、その和は25×26÷2=325平均を求めると、325÷5=65そして、真ん中の数は1~25の整数の平均の数、つまり13です。[1]の真ん中の数が 5[2]の真ん中の数が 13ふたつめにいきます(^.^)[1]で、5を中心に、点対象の位置にある数を足してみると・・・あたりまえですが・・・10になります。5と10で平均の15!(ア)+5+(イ)で、 (ア)+(イ)=15 [2]も同じことが起こるはず!13を中心に、世界は回ります。(ア)+(イ)+13+(ウ)+(エ)で、(ア)+(イ)+(ウ)+(エ)=65-13=52対象の位置にある17と9をみると、和は2652と26の関係は・・・半分になっている!!!(ア)+(エ)=26(イ)+(ウ)=26たとえば、対象の位置にある23と3も和は26!20と6も和は26になっています。これだけ分かれば、あとは簡単に答えまでたどり着けます。(1) Aにあてはまる数を求めなさい。(ア)+(エ)=26(イ)+(ウ)=26の関係を使えば、16+A=26よって、A=10 が答えです(^.^)(2) 斜線部分にあてはまる数の和を求めなさい。まず、 8 ■ ■ ■ 11となることは、OKですか?26-15=11 ですね。この11を出さないと、答えはなかなか出てきません(-_-;)したがって、■ ■ ■ =65-(8+11)=46答えは46です。☆近日中に、フリーページに、魔方陣の考え方を図入りで説明しますね。言葉だけでは、いまいちピンときませんので(^.^)つぎは、比の問題です。みなさんは、どんなイメージを浮かべて、こういう問題を解くのでしょうか?[宿題]A国、B国、C国の人口の比は30:25:2で1平方キロメートル当たりの人口はそれぞれ二千人、一万人、五百人です。A国、B国、C国の面積の比を最も簡単な整数の比で表すと、□:□:□です。渋谷教育学園渋谷中学校(つづく)
2005.07.31
コメント(1)
-

Rくん、剰余系を使う(13)
☆東京は暑かった・・・きょうは、日記を書くのが遅くなりましたm(__)m実は、四国のわらし仙人が東京の渋谷でセミナーを開催しました。下記のベストセラーを書いている、あのわらし仙人です。そのセミナーに参加しました。・夢とお金が押し寄せるわらし仙人の「売れる自分」のつくり方・わらし仙人の30倍速読術・普通の人が本を書いて怖いくらい儲かる秘術わらし仙人、チタン合金マンさん、セミナーをいっしょに受講したみなさん、どうもお世話様でした(^.^)こうして、二重の意味で暑い日になりました(^.^)セミナーの内容はもりだくさんでしたが、「ブーム」という言葉がとても印象に残りました。これから何がブームになるのか、そのブームを先取りして読む方法という話がありましたが、ブームこそ、これからの時代を生き抜くポイントであると思いました。そのために、これからの時代に身につけておくべきこととは?これは、うちの塾に来ている子たちに、早速話します(^.^)大人も同じです。Life-long Scale Education 『生涯教育』の時代です。自分磨きをしていかないと、あっという間に旧式な人間になるという時代です。このスピードは加速されていきます。今のこどもたちはそういう波をもろにかぶっていきます。マックはほぼ毎日、海岸を散歩しています。波が絶え間なく押し寄せてきます。その波を背に逃げようとすると、ときに溺れます。泳いでいて、1度溺れかかりました。引く波に吸い寄せられるのです。小学4年のときです。そのとき、死ぬかもしれない・・・と思いました。この様子に気づいた父が、浜辺の方から、「沖に逃げろ」と声をかけてくれました。波に逆らって岸に向かうから、波の引く力から逃げられなかったのです。それで、波の力に身を任せ、沖に出ました。すると、体が急に軽くなり、再び泳げるようになったのです。父の姿が、すぐそこに見えました。あのまま波の力に逆らっていたら、溺れていたと思います。人生という波も、逆らっていると溺れれます。そういう大波が2年くらいでやってくる・・・きょうのセミナーでの最大の収穫でした(^.^)■■■ Rくん、剰余系を使う(13) □□□□[前回の宿題]整数AをAのそれぞれの位の数の和で割り、余りを[A]で表すことにします。たとえば、[123]については123を1+2+3の6で割ると余りは3なので、[123]=3となります。また、[7]は、7を7で割ると割り切れるので、[7]=0[[98]]は、[98]=13なので、[[98]]=[13]=1となります。(1) [58]、[[862]]をそれぞれ求めなさい。(2) Aが2けたの整数のとき、[A]が最も大きくなるような Aを求めなさい。(3) [[A]]=9となる整数Aのうち、最も小さいものを求めなさい。 桐明中学校(1)剰余系で表せば、[58]≡( ) mod(5+8)ということです。 58を13で割れば、余りは6 答え 6[[862]]は、2段階で、まず[862]≡( ) mod(8+6+2)だから、862を16で割ってあげましょう。すると、余りは14[[862]]=[14] mod(1+4)14を5で割れば、余りは4です。[[862]]=[14]≡4答え 4(2)問題文がとてもわかりにくいです。マックも、・・・正直に言います・・・一度目に読んだときには、何のこと? という反応でした(^.^)[A]が最も大きくなるような・・・という文章は、余りが最も大きくなるような・・・と通訳しないと、ピンときません。それで、余りが大きくなるって、割る数が大きいほど、理想的!このことに気がつかないと、前に進めません(-_-;)ここが、「飛躍」です。ところで、割る数が大きいって、どんなことなの?[A]≡( ) (mod 割る数 )この割る数は、2けたの各位の和です。思いっきり大きく取ると、99はどうでしょう。[99]≡( ) (mod9+9) それで、99を18で割ってみると、余りは9[99]≡9 (mod18) なんか、小さいですね。余りが17になれば、答えなのですが・・・・・98はどうかな?[98]≡( ) (mod9+8)[98]≡13 (mod17)この逆の89では?[89]≡4 (mod17)これは、ダメでした。18,17で割って、今のところ、最も大きい余りは13。97と79で試してみましょう。[97]≡1 (mod16)[79]≡15 (mod16)おや!新記録更新です!最も大きい余りは15になりました。そして、この記録をぬくことは、もうできません。割る数が16、余りが15この先、16よりも小さい数で割っても、余りはかならず15より小さくなります。答え 79(3) (2)に比べれば、ましな問題です。[[A]]=9剰余系で表せば、[[A]]≡9 (mod Aの各位の和)こんな形なら、理想的です。[[A]]≡9 (mod10)ということは、[[A]]≡9 (mod1+9)[[A]]≡9 (mod2+8) ・・・最も小さいAを見つけるためには、[[A]]≡9 (mod1+9)が使えると、いいですね(^.^)では、[A]≡19とおいてしまいましょう。これを何で割ればいいのかというと、[A]≡19 (mod Aの各位の和)割る数が20なら理想的だけれど、[A]≡19 (mod 20)「20で割って余りが19になる数Aって?」B=A-19 としたら、「20で割って余りが0になる数Bって?」ということと、同じですね。 もうひとつ、Aは ( ア )+( イ )+( ウ )=20 になり、 ( イ )は奇数 ( ウ )は9になる! ということです。だから、( ア )+( イ )=11 候補は、8と3,6と5,4と7,2と9 しかありません。このうち、最も小さくなるのは、2と9アが2 、イが9、ウも9 という組みあわせが答えです。 答え 299お疲れ様でした。つぎは、やさしめの問題です。[宿題]38を割っても、54を割っても6余る整数をすべて求めなさい。 明治大学付属中野中学校(つづく)
2005.07.30
コメント(1)
-
数の動きって? その41
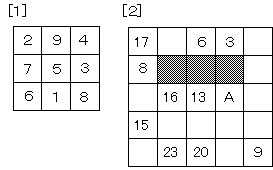
☆魔方陣というと、おどろおどろしい魔の数の世界?のようです。でも、秩序だって数を並べていけば、魔方陣が、だれにでもすぐにできてしまいます(^.^)なんといっても、3×3の魔方陣が基本です。この魔方陣、知っておくべき性質が3つあります。それはいつかまた、取り上げることにして、次の問題に挑戦してみてください。■数の動きって? その41[問題][1]と同じ規則で、[2]についても1~25の整数を並べます。このとき、次の各問いに答えなさい。(1) Aにあてはまる数を求めなさい。(2) 斜線部分にあてはまる数の和を求めなさい。 栄東中学校(つづく)
2005.07.29
コメント(0)
全323件 (323件中 1-50件目)
-
-

- 共に成長する家族!子供と親の成長日…
- はじめまして
- (2024-10-26 13:01:20)
-
-
-

- 0歳児のママ集まれ~
- P5倍😀資生堂 ベビーパウダー プレ…
- (2024-12-03 20:34:19)
-
-
-

- 大学生母の日記
- 娘が可愛いと褒められて自己肯定感上…
- (2024-11-30 21:13:19)
-








