2013年05月の記事
全11件 (11件中 1-11件目)
1
-

雲取山 その3 ---課長・快調・体調---
初日は雲取山手前で一泊です。夜8時に就寝し、朝2時に起床しました。同室の8人はまだ夢の中です。するりと部屋を抜け出しました。当然ながら山の中です。目を覚ますと山にいるのはいつも不思議な気持ちになります。山中他界。食堂にあった本をランタンの明かりで読みながら、夜明けを待ちました。図1 : 朝食朝食は朝5時半です。豆・昆布・フキ・鮭・海苔・生卵に御飯と汁物です。 『具合が悪いんかな・・・』ご飯をお代わりしながら親友Sがぼそっと呟きました。昨夜はご飯を一杯しか食べれなかったので、体調が気になったそうです。しかしそれは親友Sの勘違いでした。昨夜、自分がご飯をお代わりする際に親友Sの茶碗を見るとご飯が一口しか残っていなかったので、ついでにご飯を入れてあげたのです。当然ご飯をよそったことに気が付いていると思いましたが、それは違いました。親友Sはご飯をお代わりしようと茶碗を手にとり、ご飯がこんもり茶碗に入っていることに驚いたそうです。そして 『山登りで疲れていて、ご飯を食べたのは気のせいだったのか』と考えたそうです。・・・そんなアホな。かくしてご飯を一膳(実際は二膳)しか食べなかった親友Sは可哀そうな事に、 『体調』 と 『課長K』 を気にしながら就寝したのでした。そんなこんなで体調に関しては解決しましたが、課長Kに関しては帰ってから極秘捜査をすることになりました。----------歯を磨こうと水場に行くと、先客がいました。図2 : ヤママユガ科 オオミズアオなかなか重量級です。図3 : オオミズアオ 御尊顔雄のチャームポイントは、フカヒレのような触角です。脚が紫色なのもお洒落です。大きな蛾は不思議と手乗りできるのが面白いものです。やがて窓から、ばたばたと重そうに飛んでいってしまいました。図3 : 朝6時出発 親友S雲取山山頂を目指して白岩山から霧藻ヶ峰を縦走し、三峰神社までいくルートをとりました。このルートは方角と標高が常に変わる為、植生も場所により大きく異なります。景色がころころと変わるのが写真から分かると思います。図4 : 奥に見える山は約1550メートル (撮影・S)図5 : 熊笹の急坂を登る親友S図5は等高線に対して垂直に登るという、小細工なし問答無用のルート。雲取山山頂まで一気に登ります。図6 : 雲取山山頂からのぞむ4時間かけて雲取山山頂に到達しました。(内、写真撮影で1時間使用。ううむ・・・。)図6で見えるような山の峰を、つらつらと辿るのが縦走です。今回の縦走も、図6と似たような形状です。次は峰を歩いて、白岩山を目指します。図7 : 台風の被害根こそぎ。図8 : 鹿鹿の群れに何度も驚かされました。なにせ熊が出没するところなので気が抜けません。図9 : 白岩山へ足元の岩が、雲取山のとは違ってきました。この岩石は石灰石を含んでいるので、白岩山なのだと思います。(続く)----------
2013.05.31
コメント(4)
-

雲取山 その2 ---傾く世界---
急斜面を何時間も歩いた為か、写真撮影で水平が取れなくなりました。うまく撮影できても度が過ぎた斜面は、その傾き具合が伝わりにくくて困ります。図1 : 直立不動のホモサピエンス (撮影・S)図1は人間が立っていないと、良くわからない画像になってしまいます。ためしに指でホモサピエンスを隠すと、地面を斜めに撮った画像に見えます。図2 : このはしわたるべからず (撮影・S)しばしばこのような丸太に板を載せた橋を渡ります。よくもまあこんなにも太い丸太を使用したもんです。感服しつつ、そっと橋の端を渡ります。図3 : 友人S先に友人を渡らせて様子見です・・・よし、大丈夫そうだ。図4 : 倒木をくぐる (撮影・S)おそらく台風の被害です。ひっかからないように慎重にくぐります。図5 : 考える人 (撮影・S)自分は高いところが好きではありません。この橋の板がずるっと動いた時は、久しぶりに声を出して驚きました。図6 : 休憩中の親友S図7 : そろりそろりと (撮影・S)図9 : 山小屋今宵の宿に到着しました。思わず笑みがこぼれる親友S。図10 : (撮影・S)間違えて、未開の部族の村に侵入してしまったわけではありません。ここは温泉がある山小屋です。ちょっと中途半端な場所にあるので、もう少し先の山小屋に泊まるのが一般的です。図11 : 部屋ここの山小屋は80人が宿泊できます。自分達は図11の部屋 『けやき』 に案内されました。図12 : 食堂この食堂向かいでは、大きな竃で湯をわかしていました。 『お釜の横でオカマ座り』という、山小屋主人が爆笑した自分の写真があるのですが、掲載は見合わせます。図13 : 夕食上段(梨・グリーンリーフ・鹿のローストビーフ・ホウレン草のおひたし)下段(舞茸とシソの天麩羅・厚揚げと蒟蒻と筍の煮物・鮎の佃煮)夕食はこれと、汁物とご飯です。夕食の席に案内されると、なんと同じ登山口で降りた人(Kとする)と再会をしました。そして、自分の隣にはアメリカ人のダニエルが。(誰だこいつ)ダニエルは特別にカレーを作ってもらったようですが・・・Oh・・・ダニエル。スプーンが付いているのに箸でぎこちなく食べるなんてクレイジーな奴です。何やらダニエルは宿には泊まらず、テント場で野宿するとのこと。テントもなしで、寝袋むき出しで寝るそうです。Oh・・・ダニエル。やっぱり君はクレイジーボーイだ。(おっさんだが)箸でカレーと格闘しているダニエルに気を取られていると、親友Sがそっと耳打ちをしてきました。 『向いの人(Kのこと)、たぶん隣の課の課長だと思うんだけど・・・』そんなまさか。しかしさりげなく住まいを聞いたところ、社員が多く住む地域でした。その課長と親友Sは課が違うので直接の面識はないけれども、気になるそうです。そして親友Sはもんもんとした気持ちで床に着きました。しかしそれだけでなく、親友Sはさらにもうひとつ心配事を自分の所為でかかえていたことが翌日判明しました。(続く)----------
2013.05.30
コメント(6)
-

雲取山 その1 ---東京都最高峰---
埼玉県・山梨県・東京都の境界三重点である標高2017メートルの雲取山は、東京都最高峰であり、日本百名山の一つです。その雲取山に親友のSと二人で一泊二日のプランで登ってきました。----------新宿駅から2時間程で、東京都最西端の奥多摩駅に到着です。到着時間は9時頃でした。土曜日でしたが思いのほか人が少なく、バス停から離れたところでのんびり朝食の駅弁をつついていると・・・図1 : 奮発した朝食蜂の巣をつついたように、突然駅から群衆が飛び出してきました。弁当を小脇に抱えてあわててバス停へ。図2 : 200人以上がバス停へ自分たちは無事に乗車できましたが、1台のバスに群衆が次々に乗り込み車中は阿鼻叫喚の巷に。屋根に人が乗っていれば、さながらインドのバスです。年配の方々のボヤキを聞きながら、登山口へ出発です。図3 : バス車内から奥多摩湖をのぞむ雲取山へは、鴨沢ルート・お祭りルート・日原ルートの3つがメインです。自分たちが選んだ親川ルートはマイナーであるためか、そこで下車したのは他に1人のみでした。(実はこの1人とは山小屋で再会し、友人を悩ませることになるが、それはまだまだ先の話)図4 : 親川ルートを登り始める (撮影・S)黄色のザックは自分です。図5 : 木に巻きつく木に巻きつく (撮影・S)大木に木が巻き付いていました。登山の撮影で困るのが、風景だけではスケールがわかりにくいことです。しかたないので、いやいや自分が木に巻きつきました。(現像してみると嬉しそうでしたが)図6 : 難所1図6の看板は、最初の目的地 『丹波天平』 を指しています。しかしここで道を間違えてしまいました。倒木に沿って右方向へ道が続いていたのですが、それは間違いでした。正しい道は、この倒木の向こう側だったのです。図7 : 難所1を右へ倒木に沿って道を右へ進むと図7にでます。ほんのりと道が続いているのですが、これまでに何人かが歩いたのでしょう。気が付くと身動きがとれないほどの斜面に立っていました。 『迷ったら引き返す』という山の鉄則に従い、苦労して来た道を引き返しました。そして、難所1の倒木の向こう側を覗き、正規ルートを見つけました。道が見えていたので、コンパスでの確認を怠ったのが迷いの原因でした。後人のために、間違いルートに枝でバツ印を組みました。また、赤いテープを巻いた丸太を倒木に縛り付け、正規ルートを示しておきました。図8 : 充電中・・・ (撮影・S) 「このまま撮影しても、木のうろの大きさがわかりにくいな・・・」 はいはい。わかりましたよ。図9 : 丹波太平図9が最初の目的地、『丹波天平』 です。 中央右に小さく自分が写っているスケールからわかるように、相当に広いです。ここは山の峰ですが、あまりにも平らな地面が広がっているので、ここが山の頂上だとはその場にいても実感できませんでした。だから 『天平』 なのでしょうけど。図10 : 丹波天平登山では、こういう平らな土地は要注意です。斜面がないために現在位置がわかりにくく、容易に道に迷います。必ずコンパスで現在位置と方角を認識して歩かなくてはいけません。こういう場所でガスに巻かれるともう最悪です。(続く)----------
2013.05.29
コメント(2)
-
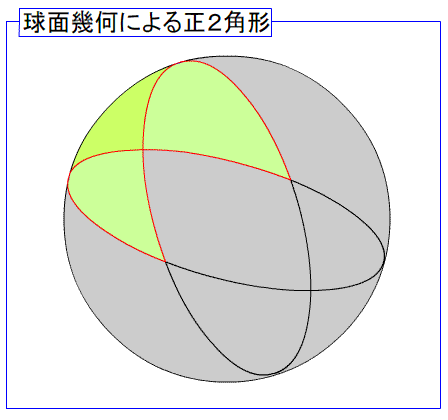
【数楽パズル】 夜長にパズル5-1 ---その知識は食えん酸---
正2角形とは図1のような図形です。図1球体表面でリングを2つ交差させてできる 『くし型』 が、正2角形となります。揚げ物に添えられたレモンのくし切りを手に取り、非ユークリッド幾何における正2角形の話でもすれば、食卓に興が添えられます。相手がすっぱい顔をしていても気にしてはいけません。おそらくレモンが沁みたのでしょう。----------この正2角形は、何か特別な利便性を持っているわけではなく、ただ、正2角形であるだけの図形です。面白い特性を無理やりひねり出すなら・・・ 『平行線が交わる』ということでしょうか。この 『平行線が交わる』 は、平面では決してあり得ない条件であり、また平面では決して許されない条件です。このことは、平面幾何つまりユークリッド幾何の 『公準5』 というルールでしっかりと(ぐだぐだと)要請されています。----------
2013.05.29
コメント(0)
-
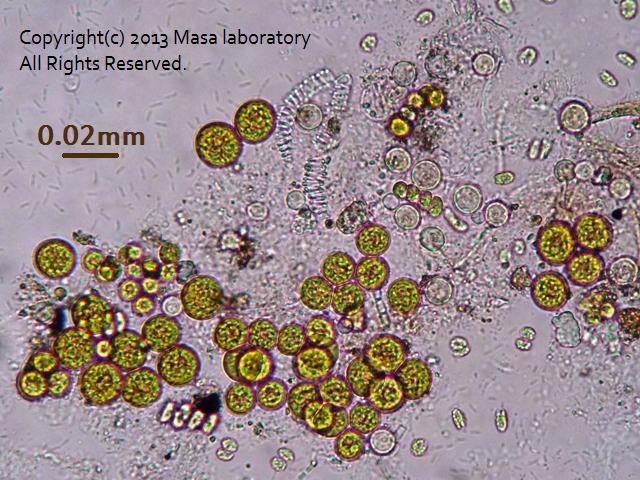
【ミクロの世界】 スプリング・スプリング・スプリング ---春の泉に沈むバネ---
和尚 「おい一休。そんなに豆を食べるでない。目上の者に譲らんか」一休 「わかりました。では私は1粒づつ食べますので、和尚さんは2粒づつ食べてください」和尚 「よかろう」・・・さて、どちらが豆を多く食べられたのでしょうか。正解は、箸で2粒の豆をつまむのは至難の業です。図1 : ヨツメモ(四目藻)の一種前話はいつも通り何の意味もありません。図1には様々な微生物が確認できます。 最初に摘まみたくなるのはどれでしょうか。図2 : ジュズモ(数珠藻)の一種数珠とはセンスあるネーミングです。ただ円形が連結しているから数珠。。というわけではないのです。図2のジュズモの真ん中部分でも確認できるように、ジュズモにはたびたび 『大きな玉』 が形成されます。(その役割は後日掲載予定)それはまるで、数珠でいうところの親玉ではないでしょうか! 自分 「そこまで考えてジュズモと名付けたのなら、もう感嘆するばかりです」 TH 「・・・数珠の親玉って何ですか?」----------植物の残骸としてよく見かけるものとして、維管束があります。図3 : 植物の維管束バネの中に微生物が挟まっていたら面白いのですが、そんな間抜けなやつは今のところ確認したことがありません。----------
2013.05.22
コメント(5)
-

【数楽パズル】 夜長にパズル5 ---ねじれた性格はゆがんだ世界の所為です---
三角形の3つの角度を全て足すと、180度 になることは誰しもが知っています。そうなると、ある問題が浮上します。 「三角形の3つの角度を全て足して、180度を超えることはないのだろうか」答えとしては、『ある』 です。例えば、3つの角度がすべて90度である三角形が存在します。さて、どのような三角形でしょうか。 解答は下にあるので、脳みそを刺激しつつ少し考えてみてください。勿論、三角形の辺はすべて直線です。----------【考慮中のおまけ画像】図1 : エウクレイデス----------3つの角度がすべて90度である三角形は、例えば次のような図形です。図2図2の三角形は、3つの角度がすべて直角です。このような、三角形の内角の和が180度を超えるような図形を、『非ユークリッド幾何学』 と呼びます。一方、三角形の内角和が180度であるいわゆる「普通の」図形は、『ユークリッド幾何学』 と呼びます。ユークリッド幾何学は、図1のおっさんの著書に由来しています。(ユークリッドは、エウクレイデスの英語読み)図2を見て分かるように、非ユークリッド幾何学は空間がゆがんでいます。空間がゆがむことにより、一見不可能な図形(例えば、3つの角度が直角の三角形)も存在し得ることができます。ただこれは取り立てて不思議な図形ではありません。私たちが持ってる『常識』が、非ユークリッド幾何学のような存在を奇妙に感じさせているのです。----------ここまでの話は、そのうち書くつもりの『例えば宇宙は11次元』の前話と、次のクイズのための布石でした。----------では、ここでクイズです。 正2角形はどのような図形でしょうか。正3角形の誤植ではありません。正2角形です。解答は、来週の月曜日の予定です。----------
2013.05.19
コメント(2)
-
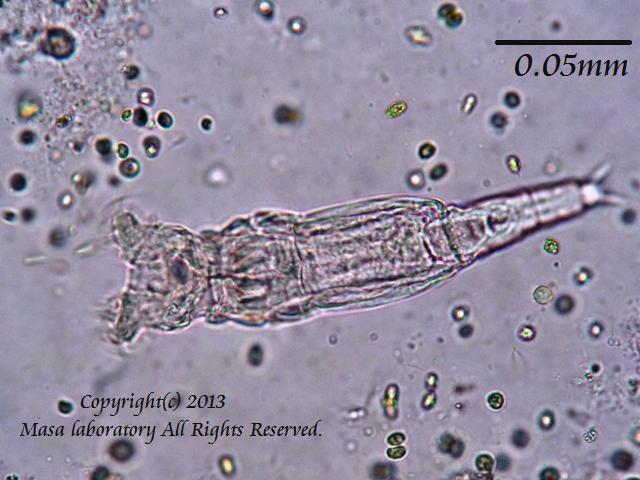
【ミクロの世界】 少数精鋭vs人海戦術 ---喰うか喰い残すか---
道路清掃車のごとく、二つのブラシを回しながら獲物を食らっているワムシがいました。緑藻プランクトンの集団に突進です。図1 : ヒルガタワムシ図1は、左側の頭部にある輪盤(りんばん)と呼ばれる器官を高速で動かしているところです。輪盤は頭部の左右でピントがぼやけている箇所です。移動中は輪盤を動かさず、移動を停止してから輪盤を動かします。図1 : ヒルガタワムシの頭部輪盤の繊毛の動きはあまりに早いので、うまく映りません。ずもももも。 と聞こえてきそうな動きでした。図2 : ヨツメモの一種4つセットの塊がいくつか集合しています。密集していればサイズが大きくなるので、捕食される可能性が減ります。普段は大繁殖して得意げな彼らですが、ビーカー内では圧倒的に少数派であり、ぽつぽつと小さなコロニーを作って遠慮がちでした。図3 : ゾウリムシビーカー内ではゾウリムシが跳梁跋扈していました。このビーカー内において、彼らの悪行を咎める者は存在しません。----------
2013.05.17
コメント(6)
-
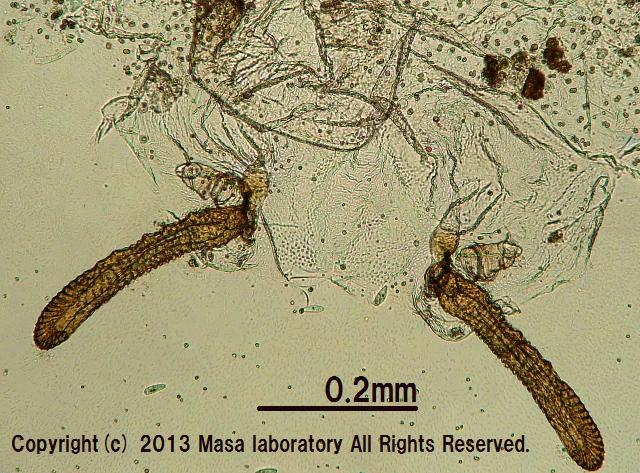
【ミクロの画像】 水面を歩く小虫 ---トビムシ---
蓋付きビーカー内で華麗にくねっていたボウフラもどき達が、旅から帰ってくると消えていました。日の当たる場所にうっかり放置してしまったため、水温が上昇し死んだようです。遺骸の痕跡すらない、見事な消滅振りでした。100匹以上のボウフラの遺骸は、1週間ほどでプランクトンたちに微塵も残さず喰われた様です。今回の舞台は、そんな集団失踪事件が起きたミステリーなビーカーです。図1 : トビムシの一種トビムシの外骨格です。中身があまりない触覚は人気薄だったようで、取りついている微生物は皆無でした。残っている外骨格も、やがて消滅します。ちらほらとゾウリムシが確認できます。図2 : トビムシの触覚図3 : トビムシの触覚確かに、堅そうで分解がしにくそうな部位ではありますが、素揚げにすると美味しそうです。----------
2013.05.16
コメント(2)
-
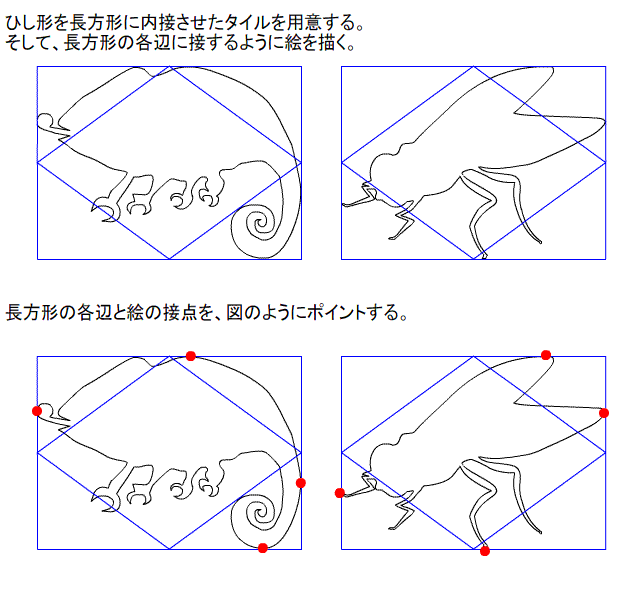
エッシャーの反転錯視タイリングの作り方 ---訂正版---
不思議絵で名の知られているエッシャーの作品に、『空と水』 というのがあります。空を飛んでいる鳥の絵が、画面下に行くにつれて魚に変化するという版画です。この作品は非常に数学的であり、簡単に言うと座標の平均値で求められます。今回紹介する手順は、上下の絵を2つ用意してから作るタイプです。エッシャーは中心の絵を用意してから作っていたようです。----------図形を別の図形に変形させることを、モーフィングと呼ぶことにします。この切りとった赤線を、もう一つの図にモーフィングさせれば完成です。以下は、モーフィング例です。今回は手作業でしたが、コンピューターを使えば綺麗に仕上がります。ここを仕上げれば、ほぼ完成です。途中で線の色が赤や黒になっていますが、2色のペンを用いてモーフィングした名残なので、色の違いに意味はありません。----------今回は手作業でしたが、コンピューターを使えばモーフィングが簡単にできます。*のように三方向からのモーフィングもできるはずです。----------
2013.05.12
コメント(3)
-

エッシャーの反転錯視タイリングの作り方 ---例えば、こう作れる---
----------(掲載後削除)掲載図に誤りがあったので記事を丸ごと削除しました。訂正したら、後日載せます。----------【替わりの小話】GWにとある山を、親友と二人で四泊五日の日程で走破するつもりでした。しかし二日目に遭難し、三日目に最初の道に出た為そのまま下山しました。どこで遭難したのかは恥ずかしいので秘密ですが、秋に再チャレンジします。その時にまた書きたいと思います。上の画像は、遭難したことにまだ気が付いていないときに遭遇した廃屋です。この廃屋の横を通り、およそ3時間後に遭難したことに気が付きました。----------
2013.05.11
コメント(4)
-
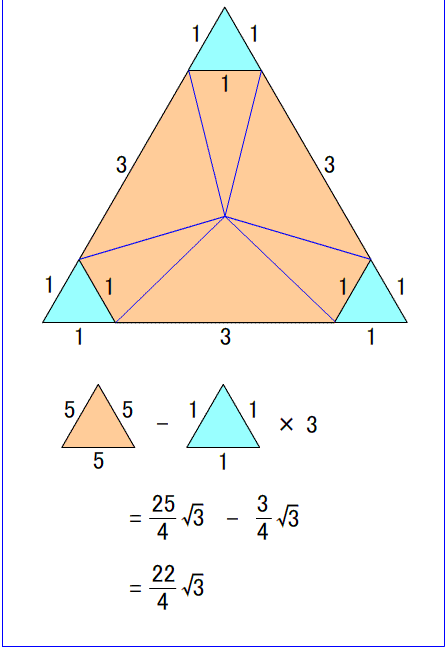
【数楽パズル】 夜長にパズル4-1 ---困難は分割せよ---
先週のパズルの補足です。再掲図正三角形の高さを導出します。図1図1の三角形は、それぞれの角度が30度、60度、90度であり、その辺の比が、1対2対ルート3 というお洒落な三角形となります。この三角形は色々と役に立つので、是非とも覚えておきたい三角形です。----------
2013.05.11
コメント(2)
全11件 (11件中 1-11件目)
1
-
-

- ラン好きです♪
- Zel.オナスタ、C.ワルケリアナfma.セ…
- (2025-11-17 15:59:22)
-
-
-

- グランドカバー
- クラピアに暗雲!主要サプライヤー撤…
- (2025-11-16 05:48:58)
-
-
-

- フラワーアレンジメント
- ビルのエントランスに ☆ アーティ…
- (2025-11-11 11:00:04)
-







