2022年02月の記事一覧 | ひできちの楽天ブログ

カシオの計算サイトでエラトステネスの篩をつくってみたとな？

カシオの計算サイトでエラトステネスの篩をつくってみましたよカシオと言えば関数電卓でございますのでこちらのサイトには沢山の計算プログラムが掲載されておりますよですがなぜか「エラトステネスの篩」による素数生成のプログラムはありませんでしたのでつくってみることにしましたよカシオの計算サイトは関数電卓でプログラムが組めるのと同じように自作の計算プログラムを作って公開して実行させることができるのですよしかも完全無料でございますよ私は計算が趣味という理系の変人でございますので1000桁の整数の計算などをしたくなってしまうのですがカシオの計算サイトは50桁の精度で計算が可能なプログラムを組むことができるのですよ今ではそういうプログラム言語はまったく珍しくもないのでございますがそれでも完全無料で計算プログラムの公開機能まできちんと日本語でいろいろと提供しているサイトはカシオの計算サイトくらいしかないと思いますな急になぜか思い立ってしまいましていくつか自作して公開しておりますがそのうちの１つがこちらの「エラトステネスの篩」でございますよカシオの計算サイトでは自作プログラムのソースコードを公開する機能がありませんのでどうしたもんかと思いましたが自作プログラムの説明欄に別サイトへのリンクを設定することは可能でしたのでこのブログ記事にリンクをしてソースコードを掲載したいと思いますよdo{MAXsieve;numeric sieve[0];numeric sieve[MAXsieve];maxdv = int(sqrt(MAXsieve));for (idx = 0; idx < MAXsieve ; idx=idx+1) { sieve[idx] = 1;}sieve[0] = 0;sieve[1] = 0;for(idx = 2; idx

2022/02/21

コメント(1)

全ての整数を3つの立方数の和で表すとな？

編集数を3つの立方数の和で表せるか？という数学クイズ的な問題がありますよ式で書くと任意の整数 nに対してn=x³+y³+z³ と書ける整数の組（x,y,z）を求めるということですなこの問題は立方となっているところがミソでございまして・・・負数の立方は負数となりまして和と言いつつ計算としては引き算になるために３つの立方の差し引きの計算となるために解を探索する範囲を無限にとる必要があるのですよとは言え解は簡単に見つかるケースも多いですよたとえば4^3+4^3+(-5)^3=3という感じでして3に対する解の組は（4,4,-5)ということになりますなこの問題のさらに奇妙なところは解が無限に存在するらしいと推測されておりますよ例えば1に対しての解は(1,0,0)というあほらしいくらい単純な組しか解にはならないだろうと考えてしまいますが実際には(-6,-8,9),(9,10,-12)という別解がありますよ1と2の場合では無限に解の組を生成できる以下の一般式が発見されておりますよ1に対しては(9a⁴,3a-9a⁴,1-9a³)2に対しては(1+6a³,1-6a³,-6a²)ほぉーまじかいな？と思ってしまいますが実際これらの組をx³+y³+z³ に代入して式変形してみると以下のように確かに1と2に式がまとめられてしまいますよ(9a⁴)³+(3a-9a⁴)³+(1-9a³)³=729a¹²+27a³-81a⁶+729a⁹+729a¹²-(1-27a³+81a⁶+729a⁹)=1そして1に対する2つの別解は一般式(9a⁴,3a-9a⁴,1-9a³)にa=1,a=-1を代入して得られるものですなこの問題は一般式が生成できるほど単純なもの思えないのございますがなかなか面白い問題ですな1と2以外の整数に対しても解の一般式が存在するのかどうかわかりませんがもしかするとあるのかもしれませんなというのは3に対する別解もはやり見つかっているのでございますよ別解があるということは解は無限に存在していてそれを生成する一般式も存在するのでは？と期待してしまいますな3に対しての別解ですが先の（4,4,-5)の組の他に(1,1,1)というあほらしいくらい単純な組も解になるわけですが他にも・・・(569936821221962380720,-569936821113563493509,-472715493453327032)という非常に大きな整数の組も解になるのでございますよこの整数を検算するにはエクセルや電卓では無理でございますので多倍長演算 web電卓のような桁の長い数字の計算を正確にできるものが必要になりますな569936821221962380720³+(-569936821113563493509)³+(-472715493453327032)³=185131426470358721030003064550489120286063150089838997749248000- 185131426364725746289073278168542399539619802127338908944671229- 105632974740929786381946720746443347962500088804576768 =3非常に大きな数値になりますが引き算の結果は正しく3になっておりますよこんな大きな数字が出てきてしまうのは予想できないことでありますな小さい数字の範囲で解の組が２つだけ存在するところで解は出尽くしたのかと思いきや探してみるとこのような大きな数字の組も解となっているということが最近わかったということなのでございますが数学の神様はこの大きな数字の組に一体どのような意味を持たせたのでしょうな？もしやこれはナンバーズ3を予想する鍵なのでしょうか？さて、私もこの謎解きに少し参加してみたくなりましてw³=x³+y³+z³ と書ける整数の組（x,y,z)の組を探してみましたよこれは(n,0,0)という自明な解が存在しますが意味ありませんのでこれ以外の別解を探したいと思いますよそれとn≦100については全ての自然数で解の組が発見されているということなのでn＞100の自然数を目標としたいですないろいろと調べているうちにこの問題の解を網羅しているページが見つかったのですがこのページにもw³=x³+y³+z³ の自明でない解は載っていませんでしたのでこれは別解を探してみる価値は少しあるかもしれないと思っておりますよただ前述の3の場合のように巨大な数字まで探索することはできませんので小さい値の組を見付けるという想定で調べておりますよではではまずは小さい数から確認していきますと・・・w=2 つまり n=2^3=8=x³+y³+z³ と書ける整数の組（x,y,z)の組でございますがネットで見つかる(9,15,-16) =9^3+15^3-16^3=という組がありますよ他にも(-16,-12,18)=-16^3-12^3+18^3= という組もありますよw=3 つまりn=3^3=27の場合となりますがネットで見つかる (-4,-5,6)=-4^3-5^3+6^3=27の他に(-10,-18,19)=-10^3-18^3+19^3=27も見つかりましたよw=4 つまりn=4^3=64の場合となりますがネットで見つかる (-3,-5,6)=-3^3-5^3+6^3=の他に(18,30,-32)=18^3+30^3-32^3=64も見つかりましたよなお小さい値で見つかってほしいという期待を込めてエクセルで巨大な掛け算の九九のような表を作って検索することで見つけておりますよw=5 つまりn=5^3=125の場合の解ですがネットでは見付けられませんでしたがエクセルで見つけることが出来ましたよ (-30,-40,45)=-30^3-40^3+45^3=125w=6 つまりn=6^3=216の場合の解もネットでは見付けられませんでしたがエクセルで見つけることが出来ましたよ (-32,-33,41)=-32^3-33^3+41^3=216w=7 つまりn=7^3=343の場合の解もネットでは見付けられませんでしたがエクセルで見つけることが出来ましたよ (-63,-70,84)=-63^3-70^3+84^3=343w³=x³+y³+z³ と書ける整数の組（x,y,z)の組がエクセルで探索した程度で簡単に見つかりましたので任意のw に対しても比較的小さな値として見つかると推測できますなそれから解が簡単に見つかるということは一般式があるだろうと言えますないろいろ探していたらKNOWN FAMILIES OF INTEGER SOLUTIONS OF x³ + y³ + z³ = nこちらのPDF の中に一般式がありましたよx³+y³=z³+w³ となる解の組は以下の式で表せるようですなx = 1 − (p − 3q)(p^2 + 3q^2),y = −1 + (p + 3q)(p^2 + 3q^2),z = (p + 3q) − (p^2 + 3q^2)^2,w = −(p − 3q) + (p^2 + 3q^2)^2次はこちらの検証と実際にプログラムを組んで解をリストさせてみようと思いますよというわけで今回は調べて得た解を表にしてまとめて終わりといたしますよww³xyzx³y³z³x³+y³+z³73436370-84250047343000-592704343→1に対する(9,10,-12) と同値6216-32-3341-32768-35937689212165125-30-4045-27000-6400091125125→1に対する(-6,-8,9) と同値4641830-32583227000-3276864→2に対する(9,15,-16) と同値464-3-56-27-12521664327-4-56-64-12521627327-10-1819-1000-583268592728915-167293375-4096828-16-1218-4096-172858328→1に対する(-6,-8,9) と同値ではでは。

2022/02/16

コメント(0)

多彩な機能を搭載した印刷ユーティリティソフト『LB 編集印刷3 Pro』の販売を開始 - 記事詳細｜Infoseekニュース

多彩な機能を搭載した印刷ユーティリティソフト『LB 編集印刷3 Pro』の販売を開始 - 記事詳細｜Infoseekニュース[画像1:https://prtimes.jp/i/17223/29/resize/d17223-29-759796-0.png]システムソフトウェア販売の株式会社ライフボート(https://www.lifeboat.jp/)は、印刷時に必要となる便利な機能を数多く搭載した印刷ユーティリティソフト…【全文を読む】[画像1: https://prtimes.jp/i/17223/29/resize/d17223-29-759796-0.png ]この新商品のソフトウェアがソースネクストでなんと32%Off の4480円にさらに2000円オフクーポンが適用できる限定セールを行っておりますよさらに！休日は楽天リーベイツの利率が大幅アップしますのでポイント還元も大きいですなこちらの商品は使いこなせばかなり便利なソフトウェアでございますな早速購入してみましたので別の記事にてご報告いたしますよ

2022/02/13

コメント(0)

韓国時代劇ドラマを無料で見るとな？

編集韓国時代劇ドラマに私はまったく興味はないのですが同居の家族が韓国時代劇ドラマに興味があるということでamazon prime でイ・サンが配信されているのを視聴しておりましたよ74話を約３か月かけて見終わっておりましたよamazon prime は過去の視聴履歴を参照するのも非常に快適でございますなmuscijp やvideo market も類似の動画コンテンツ配信サービスでございますがレンタル履歴や視聴履歴の表示に非常に時間がかかりましてかなり使い辛いですな話は戻りますが・・・amazon primeでのイ・サンの配信があと数日で終了となるようですな家族は全話を見終わったようですのでそれは別によいのですが次にまた韓国時代劇ドラマを見たいということになりまして・・・調べてみたところトンイがよいということになりまして早速視聴しておりますが・・・こちらもあと数日で終了となるようですなトンイも60話と非常に長いドラマでございましてさすがにあと5日で60話全てを視聴することは不可能でございますなそこで他の動画配信サービスで無料配信しているところはないか？と探してみるわけですがまず思いつくのはGYAO!ですなトンイが無料版GYAO!で配信されておりますなただ配信終了日が3月31日23:59までと設定されておりますな詳しく確認してみるとこの終了日は40話までの設定ですなトンイ　第41話 | 韓流 | 無料動画GYAO!その先の41話以降は明日から順次一話ずつ配信開始されていくようですな47話までは配信開始日が公開されておりますなおそらくですが48話以降もおなじように配信されるんでしょうなトンイ　第41話 | 韓流 | 無料動画GYAO!トンイ　第47話 | 韓流 | 無料動画GYAO!1～40話は3/31までということですななお他にもトンイが配信されているサービスがないか調べてみましたよ個人的にはmusicjp/videmarketでクーポンで無料視聴できたらと思いましたが弱小サービスでは配信できない人気作品ということのようですな【配信してない】musicjpvidemarketクランクイン！ビデオTELASA / テラサ（旧ビデオパス）DMM動画abema.tv【配信している】HuludTVU-NEXT楽天TV (見放題プラン)TSUTAYA TV (見放題プラン)

2022/02/13

コメント(0)

調和数と約数関数とは？

またまた数学についての記事でございますよ今回は調和数の値を46番目まで計算してみましたので調和数についての記事を書いてみたいと思いますよまずは調和数は英語ではharmonic numberというようですなwikipedia では Harmonic divisor number となっておりますなオンライン整数列大辞典に"Harmonic divisor number"に完全一致する記事はないようでございますが・・・まぁどちらでもいいでしょう調和数の意味でございますが{(全ての正の約数)の調和平均}が、整数値になる数ですな調和平均とは、{(逆数和の平均)の逆数}ですな【こういう説明も括弧を使ったほうが明確かなと思いますな】つまり6の場合ですと6の約数は、1,2,3,6の4つですので調和平均の計算値は2となりまして整数となり、つまり割り切れたので調和数ですな1/((1/1+1/2+1/3+1/6)/4)=2上の長い式の計算ですがwindows10 の電卓アプリに式を張り付ければ計算されますよ調和数かどうか確かめるには約数の調和平均を計算してみればよいのですが計算には約数を網羅する必要があるのでなかなか面倒でございますなまた調和平均が割り切れた場合には具体的な値も観たいですなそう考えると上記の計算式は少し変形しておいたほうが都合がよいですな1/((1/1+1/2+1/3+1/6)/4)=4/(1/1+1/2+1/3+1/6)=4/((6/1+6/2+6/3+6/6)/6)=4/((6+3+2+1)/6)=6*4/(6+3+2+1)=6*(6 の約数の個数)/(6 の約数の総和)調和数を計算するために約数を網羅するのは当然としてここまで式変形しておくと計算自体もかなり簡単になりますなこの変形した式を用いて調和数を計算して表示するPythonプログラムは以下となりますよimport sympydef main(): counter=0 for n in range(1, 10**7): ds0=divisor_sigma(n, 0) ds1=divisor_sigma(n, 1) if (n * ds0 ) % ds1 == 0: counter+=1 print(counter,n,ds0,ds1,(n * ds0 ) / ds1)main()quit()python のライブラリーに整数論用の関数が提供されておりますのでこちらを使って簡単に計算することが出来ますなソースコードの中で使用されているdivisor_sigma　は約数関数でございますな約数関数とは自然数 n の約数に関する関数でございましてdivisor_sigma(n, 0)は、自然数 n の約数の個数を返しますよ数学では、自然数 n の約数の個数は、関数d(n) で表記されることがありますなdivisor_sigma(n, 1)は、自然数 n の約数の総和を返しますよ数学では、自然数 n の約数の総和σ(n) と表記されることが多いですなちなみにdivisor_sigma(n, m)は、自然数 n の約数のm乗の総和を返しますよ計算結果は以下となりますよ番号調和数約数の個数約数の総和約数の調和平均111112641223286563414012336552701672066496109925767224201688163824436899297032864011106200241488010118128141625671281904826208151318600485952015141862036478801415278464878624171630240961209602417327609613104024185586072191520211910566428227584132011780048297600192116740096595200272217360072499968252323751096786240292424206072670320262533264019214515204426360360192157248044275394009617856002928695520192290304046297261801442681280393075348019231449604631950976842958592273210892701443734640423314212801925806080473415397201926289920473521785402168714160543622295009661152003537229026014480438404138245700025610483200603928458001921071360051404358600961130880037414713984160157132804842475488016817751552454357722001441696320049446051500144174283205045850640014424998400494688722001923214080053以降の調和数は最後尾にありますこちらの計算結果（調和数の列）はオンライン整数列大辞典にリストされている調和数と相違なく一致しておりますよ約数の調和平均の列はこちらと相違なく一致しておりますよ調和数の約数の個数と調和数の約数の総和がリストされているページはいまのところ見つけられませんでしたよ調和数の記事をネットで検索してみたところではこちらのPDFに大きな調和数がリストされておりましたので紹介いたしますよ調和数の素因子の個数についてこちらの記事は第9回福岡数論研究集会 in 別府の中で秀明大学の後藤丈志准教授が発表したものでございますなこちらの記事はタイトルの通り約数の個数ではなく素因子の重複を許した個数に着目した内容となっておりまして調和数の大きい順にはリストされておりませんな中身はまだ読み切れておりませんが・・・（省略いたしますよ）リストされている調和数の一番大きい値は82550232450186200の17桁の整数でございましたよ私は7桁の整数までの範囲でPCで計算しましたが数時間かかっておりますので上記のソースコードで17桁まで調べるのはちょっと無理でございますななおこの記事(PDF)のサーバー自体は愛知教育大学でございますな愛知教育大学の岸康弘教授が福岡数論研究集会の世話人ということでファイルが格納されているということなのでしょうなこちらのPDF記事にリストされたいる大きな調和数について抜き出してみましたよ私は46番目までしか計算することができておりませんのでありがたく利用させていただきますよ 44 605150045 850640046 887220047 1198197048 1430352049 1549548050 1616659251 1742832052 1815450053 2308880054 2396394055 2702700056 2941029057 3355033658 3703518059 4466007060 4553280061 4668300062 5040172863 5214132064 5651100065 6926640066 7125300067 7503860068 8083296069 8169525070 9040941071 11058320072 11504844073 11546262074 13789152075 14496300076 16339050077 19171152078 23310378079 25542809680 28742580081 30015440082 31817780083 32678100084 40085136085 40738698086 42318432087 45981824088 49997493089 51351300090 52648050091 54027792092 55990340093 62339760094 64427126495 67534740096 81913104097 82512080098 88640244099 900463200100 995248800101 1162161000102 1199250360103 1265532840104 1379454720105 1558745370106 1630964808107 1632825792108 1727271000109 2008725600110 2369162250111 2481357060112 2701389600113 2705020500114 2763489960115 2777638500116 2839922400117 2876211000118 2945943000119 3209343200120 3221356320121 3328809120122 3349505250123 3594591000124 3702033720125 3740553180126 4720896180127 4738324500128 5058000640129 5275179000130 5579121240131 5943057120132 7279591410133 7515963000134 8154824040135 8243595360136 8410907232137 8628633000138 8659696500139 8698459616140 10575819520141 10597041000142 10952611488143 11480905800144 12941019000145 13398021000146 13581986600147 13660770240148 14254365440149 14541754500150 15358707000151 18999981000152 20015559200153 20387256120154 21611457280155 23855232960156 24362612820157 26113432800158 27122823000159 27689243400160 27726401736161 31638321000162 32956953120163 35793412200164 42054536160165 43952044500166 50497467930167 54572427000168 54648009000169 57648181500170 59388963480171 73924348400172 80551516500173 83410119000174 87825283840175 89526646440176 93419333280177 108061356200178 110886522600179 126090783000180 142985422944181 147112449120182 150115204512183 151955343540184 156473635500185 159248314400186 164297299320187 169696449000188 221908282624189 236489897160190 250230357000191 280541488500192 311203567584193 321300067176194 350280184800195 428555439000196 470717137800197 494122282290198 583096381560199 765181053000200 819730138500201 888875820360202 888988066400203 950432517216204 995024181060205 997978703400206 1159571485800207 1161528261600208 1179832600464209 1253107608480210 1369947647250211 1413817996500212 1517389419000213 1584792261000214 2021976333000215 2096328767456216 2468667064500217 3356538237000218 3448576989000219 3622293071600220 4409499089268221 4903097162600222 5111051997870223 5914045683000224 6175225017000225 6764077878600226 9831938337200227 10256659997220228 10341947847528229 10461217539500230 14747907505800231 15337823806032232 16965637957800233 22047495446340234 29495815011600235 31094717121000236 43180427911400237 46013471418096238 47089809930800239 54934276752360240 56221571976570241 60876700907400242 71969788628304243 110204785627560244 127815198383600245 180789462659988246 181414595016200247 191722797575400248 274350998756016249 351362427945200250 352094693186600251 427721411658996252 510867516000912253 555874137793800254 685877496890040255 822207921882984256 899622357853800257 935607252167952258 1143129161483400259 1291983233155520260 1366639428870800261 2138607058294980262 3431346479682800263 6385843950011400264 61390229699943300265 82550232450186200

2022/02/13

コメント(0)

信仰治療師、男児望んだ妊婦の額に5センチのくぎパキスタン - 記事詳細｜Infoseekニュース

信仰治療師、男児望んだ妊婦の額に5センチのくぎパキスタン - 記事詳細｜Infoseekニュース【AFP＝時事】パキスタンの妊婦が、男児の出産を保証するという信仰治療師によって額にくぎを打ち込まれていたことが分かった。北部ペシャワル（Peshawar）にある病院の医師が9日、明らかにした。この医師によると、妊婦はペンチで自らくぎを抜こうとして失敗し、来院。「女性は、意識ははっきりしていたが、強…【全文を読む】

2022/02/10

コメント(0)

おもちゃのボタン電池誤飲の1歳男児、心臓に穴が開き2日後に死亡（スコットランド） - 記事詳細｜Infoseekニュース

【海外発！Breaking News】おもちゃのボタン電池誤飲の1歳男児、心臓に穴が開き2日後に死亡（スコットランド） - 記事詳細｜Infoseekニュース1歳5か月の男児が昨年末、両親の目の届かないところで小さなボタン電池を誤飲した。男児は2日後に死亡し、クリスマスイブで楽しい時を過ごしていた家族は一転、悲しみの底に突き落とされた。『TheSun』などが伝えている。スコットランド、マザーウェル在住のクリスティーン・マクドナルドさん（Christine…【全文を読む】ボタン電池（CR1616）ばら売り55円【代引き発送可】【送料無料】価格：70円（税込、送料無料) (2022/2/9時点)楽天で購入

2022/02/09

コメント(0)

数の分類

編集数の特長、性質を表す数学用語が沢山ありますが正直あまりマニアな用語は知らないなぁというものが結構あるようなのでそれらをとりあえずまとめてみようかなと思いましたよ対応する英語を把握しておきたいという目的もありますよどうせならかなり細かく網羅してみようかなと思っておりますよあと前提として数学マニア向けの分類ですので初歩的なものが抜けていると思いますよ追加が簡単なようにしたいので複雑な書き方にはしたくないのですがかと言ってもただ羅列するのもアレですからバランスとって階層図で表現して包含関係があるものは配置をネストさせてますよネストして配置しているもの和が親階層の数を完全一致するわけではないので若干ご注意くださいな（例 )また数の性質ではなくいくつかの数の組に対する性質を表す用語というものもありますが特にこだわらずに混ぜいれておりますよ数と数の関係を表す用語（逆数etc）もありますがそれは基本的には対象外にしておりますよ数(number)*多元数かどうか？→→→多元数*多元数ではない実数(real number)例　オイラーの定数(Euler-Mascheroni constant)有理数無理数(=有理数ではない)例　√2* 代数的かどうか？代数的数(algebraic number)例　√2+iプラスチック数(Plastic number)実代数的数例　∛3超越数(transcendental number)円周率π(pi)ネイピア数( Napier's constant),自然対数の底e()リウヴィル数(Liouville number)有理数(rational number)例　1.5 ,2/30(zero)正数(positive number)負数(negative number)分数(fraction)小数(decimal),有理小数純小数(pure decimal)例　0.1帯小数(mixed decimal)例　1.1* 小数表示部が有限かどうか？有限小数(terminating decimal)(無限)循環小数(recurring decimal , repeating decimal)例　0.11111...(=1/9)純循環小数(pure recurring decimal)例　1.11111...(=10/9)混合循環小数(mixed recurring decimal)例　1.3333...(=4/3)整数(integer)例　0,1,2奇数(odd number)偶数(even number)単偶数(singly even number),半偶数複偶数(doubly even number)正整数(positive integer)非負整数(Non-negative integer)自然数(natural number)* 完全数かどうか？完全数(perfect number)不完全数(imperfect number)擬似完全数(Pseudoperfect number)準完全数(quasiperfect number)概完全数(almost perfect number)乗法的完全数(multiplicative perfect number)倍積完全数(multiply perfect number)超完全数(Superperfect number)不足数(deficient number)過剰数(abundant number)不思議数(Weird number)友愛数(amicable number)社交数(sociable number)友愛的三対(amicable triple)準友愛数,婚約数(betrothed number)拡大友愛数(perfect number)サブライム数 (sublime number)* 素数かどうか？素数(prime number)双子素数(perfect number)三つ子素数(prime triplet)四つ子素数(prime quadruplet)五つ子素数(prime quadruplet)六つ子素数(prime sextuplet)いとこ素数(cousin primes)セクシー素数(perfect number)メルセンヌ素数(Mersenne prime)弱い素数(weakly prime number)極端に弱い素数(extreme weakly prime number)循環素数(Circular primes)ラマヌジャン素数(Ramanujan prime)置換可能素数切り捨て可能素数(Left truncatable prime)右切り捨て可能素数(right truncatable prime)ソフィー・ジェルマン素数(Sophie Germain prime)safe prime)安全素数(safe prime)ワグスタッフ素数(Wagstaff prime)<プロス素数(Proth prime)ピタゴラス素数(Pythagorean prime)ピアポント素数(Pierpont prime)第2種ピアポント素数一般化ピアポント素数第2種一般化ピアポント素数カルタン素数(Quartan prime)半カルタン素数(Half Quartan prime)メルセンヌ素数(Mersenne prime)二重メルセンヌ素数(double Mersenne prime)Cuban 素数(Cuban prime)キャロル素数(Carul prime)Kynea素数(Kynea prime)レイランド素数(Leyland prime)Thabit 素数(Thabit prime,321 prime)ニューマン–シャンクス–ウィリアムズ素数(Newman–Shanks–Williams prime,NSW prime)モツキン素数(Motzkin prime)合成数(composite number)確率的素数(probable prime)擬素数(pseudoprime)フェルマー擬素数(Fermat pseudoprime)オイラー擬素数(Euler pseudoprime)オイラー・ヤコビ擬素数(Euler–Jacobi pseudoprime)ペリン擬素数(Perrin pseudoprime)フロベニウス擬素数(Frobenius pseudoprime)強い擬素数(Strong pseudoprime)リュカ擬素数(Lucas pseudoprime)フィボナッチ擬素数(fibonacci pseudoprime)概素数(almost prime)多冪数(powerful number)素数冪(prime power)累乗数(perfect number)高度合成数(highly composite number)半素数(semiprimes,semiprime,biprime)完全数(perfect prime)素数階乗(Primorial)素数階乗素数(Primorial prime)四素合成数無平方数(squarefree integer)* その他の分類平方数(square number)多角錐数(pyramidal number)三角錐数(triangular pyramidal number)四角錐数(square pyramidal number)五角錐数(pentagonal pyramidal number)六角錐数(Hexagonal pyramidal number)七角錐数(Heptagonal pyramidal number)八角錐数(Octagonal pyramidal number)五胞体数(pentatope number)図形数(figurate number)多角数(pulygonal number)中心付き多角数(centered pulygonal number)三角数(triangular number)平方三角数(square triangular number)五角数(pentagonal number)六角数(hexagonal number)七角数(Heptagonal number)八角数(Octagonal number)九角数(Nonagonal number)十角数(Decagonal number)十二角数(Dodecagonal number)回文数(Palindromic number)回文素数(Palindromic prime)回文平方数(Palindromic squares)フェルマー数(Fermat number)ユークリッド数(Euclid number)クンマー数(Kummer number), 第二ユークリッド数リュカ数()シルベスター数()トリボナッチ数()カタラン数()ベル数(Bell number)スターリング数(Stirling number)メルセンヌ数(Mersenne number)二重メルセンヌ数(double Mersenne number)オイラー数(Euler Number)星型八面体数()パドヴァン数()幸運数()モツキン数(Motzkin number)ヤーコプスタール数()ウェダーバーン・エサリントン数()ゴロム数()ペラン数()カレン数()矩形数()ウラム数()カーマイケル数()ウッダル数()アルクィン数()アロンソン数()フォーチュン数()ユークリッド数()カプレカー数()楔数()ハッピー数()ファクトリオン(Factorions)魔法数()ベルヌーイ数(Bernoulli number)チャンパーノウン定数(Champernowne constant)起伏数()パンデジタル数()アキレス数()シェルピンスキー数()リーゼル数()ブリエ数()高度トーティエント数(highly totient number)タンジェント数(tangent number)セカント数(Secant Number)ピタゴラス数(Pythagorean triple)タクシー数(taxicab number)フィボナッチ数(fibonacci number)<プロス数(Proth number)ユークリッド・ムリン数(Euclid number)キャロル数(Carul number)Kynea数(Kynea number)レイランド数(Leyland number)第2種レイランド数()Thabit 数(Thabit number)ニューマン–シャンクス–ウィリアムズ数(Newman–Shanks–Williams number,NSW number)多元数(hypercomplex number),超複素数十六元数(sedenion number)八元数(octonion number)四元数(quaternion number)余四元数(coquaternion number)双余四元数(coquaternion number)双複素数(bicomplex number)二元数(binarion number)複素数(complex number)例　√2+i(√-1)* 代数的かどうか？代数的数(algebraic number)超越数(transcendental number)* 虚数かどうか？虚数(imaginary number)例　1+i(=1+√-1)純虚数(pure imaginary number)例　2i(=2*√-1)虚数単位(imaginary unit)例　i(=√-1)ガウス整数(Gaussian integer)ガウス有理数(Gaussian rational number)アイゼンシュタイン整数(Eisenstein integer)共役複素数(conjugate complex number)実数(real number)→→→実数の分類

2022/02/08

コメント(0)

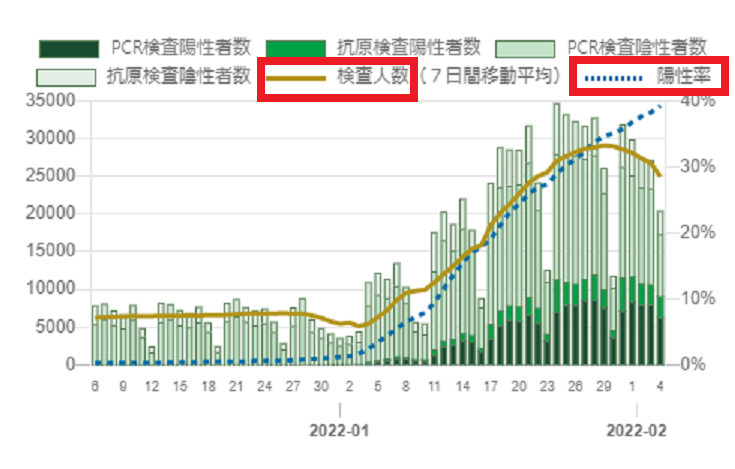
東京都のコロナ検査の陽性率 39.2 %

編集東京都が公開している情報によりますと2022年2月6日の数値（７日間移動平均値をもとに算出）東京都のコロナ検査の陽性率 39.2 %検査人数 24,934.1 人だそうですな人数でいうと同日(2/6)のデータはPCR検査陽性者数 2434人　PCR検査陰性者数2801人抗原検査陽性者数 784人抗原検査陰性者数994人検査人数(7日間移動平均)25046.3人となっておりますな人数から計算してみますと(2434+784)/(2434+784+2801+994)=0.458となりますな・・・・陽性率の値はデータファイルには0.392 とありますがこれがどういう算出方法なのか示されておらず意味不明です検査人数の2万5千人と陽性＋陰性の数が大きく違いますがこれはたぶんその日に検査結果が判明した分だけ計上されているからなのでしょうな検査の状況によっては検査日の翌日以降にもなるのでしょうなモニタリング項目(4)検査の陽性率,検査人数 | 東京都新型コロナウイルス感染症対策サイトこのグラフが示してることは検査する人数の増加と陽性率の増加には比例相関があるでございますな？違いますかね？ただ1月末から比例しなくなって陽性率がひたすら増加しておりますなどうしてそうなるの？と疑問に思いませんか？でも答えは単純にこれなのでは？ウィルスは毎年冬に大流行するのでございましてウィルスを100%回避することは不可能というか39.2 %が陽性の陽性になる検査って何を検出する検査なんですかね？それってただの確率1/2の子供相手の駄菓子屋のクジ引きでは？その39.2 %が医療崩壊を起こしているというならそれは納得迷惑な話ですなでも東京都民の39.2 %が咳してるわけじゃないでは陽性率39.2 %の意味って？病状の実態を表していない意味のない数字では？大流行してる状況では100%になってもおかしくはないという検査なのではないでしょうかね？で・・・その検査に意味はある？一方一番気になる数字である重症化の人数でございますな陽性でも自宅で待機して終わりというパターンもあればそもそも検査してない人が圧倒的に多いわけですが2万人以上検査して本当に怖い病気ならその人数が大きいはずだよね？ということになると思いますが・・・41人東京都の人口1400万人に対して陽性者の人数は先の陽性率から14,000,000*0.392=5,488,000となりまして、これに対する重症化人数の割合は41/5,488,000*100=0.00007%よくわからない％になってしまったので分数でいうと41/5,488,000=1/(5,488,000/41)=1/133853となりまして大雑把に言えば13万分のですないやグラフの傾向から見ると陽性率はもっと増加するように見えますので重症化人数の割合はもっと小さくなる可能性が高いでしょうな陽性者が重症化する割合ってこんなに低いってこと？と思いませんか？そうならPCR検査はもう意味がないと言えませんか？重症化するかどうかは年末ジャンボ宝くじを100枚大人買いして1等を当てるくらいの確率の低さなわけございますよ宝くじを買うことは叶わない夢を見るためですがPCR検査は起こりもしない悪夢をわざわざ見るための検査では？そんな検査もう終わりにしましょう重症化する確率の低さを無視してませんか？東京都で検査したら39.2%が陽性ですから笑都民全体で計算すると陽性者のうちのたった14万分の1が重症化しています一体なんの指標になるというの？PCR検査したところでそれは何も意味はないってことですよ国民の税金を使う意味のない医療行為は無料ではなく有料、保険適用外にすべきですな検査を無料だからと言って受けている人は税金の無駄遣いに加担しているように見えますよマスゴミに煽られている人冷静になりましょうよ大した病状でもないのにPCR検査して意味あるの？

2022/02/07

コメント(0)

Heart の演歌のようにしみる名曲

私が利用している音楽配信サービスはAmazon Music Unlimited でございますよ有料でございますのでそれなりの品質だったり付加価値が求められるものになりますな私は自宅で利用することはほとんどですのでPC用のデスクトップアプリを利用しておりますがお気に入りに登録しているアルバムやアーティストに関連のおすすめ情報がトップ画面に表示されるので自分が把握できていない情報を簡単に知ることができまして非常によいサービスだと思っておりますよ音質は有料サービスですので劣化した無料サービスとはやはりはっきりと違いますよ安いヘッドフォンで聴いても違いははっきりわかりますよ今回はおすすめに表示されていた2022/1/24リリースのHeart のライブアルバムの中から1曲を紹介いたしますよアルバムの視聴はこちらからできますよHeart Live In Las Vegasなんと14曲　69分のアルバムで600円というお得な価格でございますな1995/10/16のラスベガスでのライブをアルバム化したmp3のダウンロードでございますので決して話題性のあるものではありませんので安くないと困るのではありますがそれにしても600円とは・・・Amazon Music にはこのアルバムと全く同じものが複数のレーベルから公開されている状態ですのでおそらくは流出ものが普通に流通してしまっているということなのでしょうな？よくわかりませんが・・・それはさておき紹介したい曲はHeart　のアン・ウィルソンのボーカルによるヒット曲でございますよAll I Wanna Do Is Make Love To You (Live)この曲は1990年にヒットしたロック・バラードでございますよいわゆる80's の商業ロック・サウンドということになりますかなHeart　にアン・ウィルソンが加入したのが1971年ということでして今現在はなんと71歳（1950年6月19日生まれ）でございますなこの曲はHeart がスタジオ・アルバム制作をしないようになってから原曲のテンポをかなり落としてほとんど別の曲のようにリメイクされておりますなこのリメイク版が最初に音源化されたのもはやりライブ盤だと認識しておりますよこちらでございますなThe Road HomeこちらのアルバムにはHeartが大手レーベル（capital）から1995年に発表したライブアルバムですなそしてこちらにもテンポを落としたリメイク版のAll I Wanna Do Is Make Love To Youが収録されておりますよ同じ曲の2つの音源ですがライブで歌っているものの収録ですのでこの曲が好きなら聞き比べるのも楽しいことでございますなとにかく実力がありすぎる歌手なわけで歌い方も変えてきたりアドリブを入れてくれるだけでファンとしてはうれしいわけですなさてそのアン・ウィルソンですが71歳で今も現役でステージでばりばりに歌っておりますよ日本の歌手ではそういう歌手は演歌のジャンルにしかいないのではないでしょうか？そしてアン・ウィルソンほどのハリがあり太く伸びのある迫力の歌声を持つ歌手はそうは見つからないと思いますな年齢と実力の両方で比較できる日本の現役女性歌手を探してみますと・・・石川さゆりはまだ64歳ということで話になりません笑八代亜紀が71歳で現役のようでございますが実力はどうでしょうか？はっきりいって比較にならないと思いますが・・・声で勝負になるかもしれないというのは天童よしみが挙げられると思いますが67歳ということでこれも若干まだまだ青いなという感じですなそして身長147㎝というサイズではアン・ウィルソンと比較するのはそもそもちょっと無理があると思われるわけですななににろアン・ウィルソンは身長 170 cmもあるそうですし体重も相当なものと推測されますのでその身体的能力で勝負になる日本人女性歌手が簡単に見つかるはずがないのですなたしかに全盛期のHeartの二人の姉妹の見栄えはド派手でバンドの中の男性メンバーの中でも小さく見えませんでしたし相当なインパクトがありましたな身体的な比較でいうと和田アキ子が71歳でなんと174 cmということでございますな和田アキ子の全盛期のころの歌声も迫力があったように思いますがはやり実力ではアン・ウィルソンには全く及ばないでしょうなしかしまだ現役であり日本人でありながら身長でアン・ウィルソンに勝っている点はかなり評価できますなということでアン・ウィルソンを日本人女性歌手で例えるなら和田アキ子と天童よしみ　二人分という表現がいいのではないかと・・・・アン・ウィルソンはyoutubeチャンネルを開設しておりましてこの曲の動画もありますのでそちらも紹介いたしておきますよAnn Wilson of Heart - YouTubeAll I Wanna Do Is Make Love To You - Ann Wilson of Heart

2022/02/03

コメント(0)

異なる素数の平方の和となる最小の素数は?

前回の記事が異なる2つの素数のべき乗の和は素数になる？ならない？最小の素数は？というお話でございましたが今回は平方に限定して和を取る素数の個数を増やしてみたいと思いますよではではどんどん確認していきますよ異なる2つの素数の2乗の和となる最小の素数は？132 ^ 2 +3 ^ 2 =これは調べるまでもなく最小値且つ素数ですな異なる3つの素数の2乗の和となる最小の素数は？833 ^ 2 +5 ^ 2 +7 ^ 2 =これも調べるまでもなくという結果の式ですなちなみに2^2 を残してしまうと残りが奇数素数の2乗が偶数個となりますから式全体としては偶数になってしまいますので2^2は含めない形の式が最小値の候補となりますなその形の式ではこれが最小値ですので調べるまでもないですなこの考察から素数個数が奇数の場合には2^2を残さない式が最小値になりますなこの小学生レベルの結果でございますがなんととある大学の理系学部のHPに演習問題として掲載されておりますよ「異なる3つの素数の平方の和は素数になり得ない」という命題の証明問題でございますよもちろん83という素数が示す通りこの問題自体が間違っているのは明らかですな証明内容を読んでみましたが、いやいやちょっと待ってくれと突っ込みたくなる内容でしたよ大学の学問という数学は極めて受動的な態度で学習する傾向が高いので証明が間違っているという見方ができなくなってしまうことがありますよこの問題はまさにその典型と言えるでしょうな異なる4つの素数の2乗の和となる最小の素数は？1992 ^ 2 +3 ^ 2 +5 ^ 2 +7 ^ 2 =これも調べるまでもなくという結果の式ですなこれは単なる偶然であるはずですが興味深い結果ですな異なる5つの素数の2乗の和となる最小の素数は？373(9, 25, 49, 121, 169)3 ^ 2 +5 ^ 2 +7 ^ 2 +11 ^ 2 +13 ^ 2 =これも奇数個の場合の2^2を含めない最小値の式そのままですな異なる6つの素数の2乗の和となる最小の素数は？5692 ^ 2 +3 ^ 2 +5 ^ 2 +7 ^ 2 +11 ^ 2 +19 ^ 2 =ここで初めて最小となる式よりも大きい式が素数となる結果となりましたなまぁさすがに常に最小となる式が素数になるというようなことは考えられませんのでもう少し先まで調べてみたいと思いますよちなみにその次に大きい素数はちょっと面白いですぞ6172 ^ 2 +3 ^ 2 +5 ^ 2 +7 ^ 2 +13 ^ 2 +19 ^ 2 =2 ^ 2 +3 ^ 2 +5 ^ 2 +11 ^ 2 +13 ^ 2 +17 ^ 2 =この617という素数は2通りの素数の2乗の和の組み合わせができますよほんまかいな？ということで、２つの式をWindows10の電卓アプリにペーストしてみてましたが。確かに同じ617の値になりますな。このような特徴をもつ素数が他にもあるのかどうか？また別の機会に調べてみたいと思いますよまた２つの式を簡単にすると7 ^ 2 +13 ^ 2 +19 ^ 2 =11 ^ 2 +13 ^ 2 +17 ^ 2 =579ということですな両辺を比較しやすく少し書き足しますと…素数ｐ711131719ｐ²49121169289361579=7^2+13^2+19^2=11^2+13^2+17^2というなかなか美しい関係になっておりますな素数関連の小ネタとして覚えておきたい式ですなまたこの式の計算値である579も覚えやすいのですがしかし579は素数ではないのが非常に惜しいような気がしますな・・このような形が成り立つ素数の組み合わせは他にもあると思いますのでそちらも調べてみたいと思いますよ異なる7つの素数の2乗の和となる最小の素数は？15435 ^ 2 +7 ^ 2 +11 ^ 2 +13 ^ 2 +17 ^ 2 +19 ^ 2 +23 ^ 2 =この式は3^2を抜いて、素数の中で9個番目に大きい23を追加したという形ですので候補の式としては最小値ではないですなこの１つ抜く素数を選ぶ場合、大きい素数から選択したほうが式全体としては小さい結果になりますなですので7番目の19^2を抜いて、素数の中で9個番目に大きい23を追加した次の式ですな3 ^ 2 +5 ^ 2 +7 ^ 2 +11 ^ 2 +13 ^ 2 +17 ^ 2 +23 ^ 2 =こう考えると、1543の式は、8番目の最小値ということになりますな最小値候補の式の件数は少ないので実際に検証してみましょう最小値となる式は3 ^ 2 +5 ^ 2 +7 ^ 2 +11 ^ 2 +13 ^ 2 +17 ^ 2 +19 ^ 2 =1023(≠素数　3が約数)2番目の最小値となる式は3 ^ 2 +5 ^ 2 +7 ^ 2 +11 ^ 2 +13 ^ 2 +17 ^ 2 +23 ^ 2 =1191(≠素数　3が約数)3番目の最小値となる式は3 ^ 2 +5 ^ 2 +7 ^ 2 +11 ^ 2 +13 ^ 2 +19 ^ 2 +23 ^ 2 =1263(≠素数　3が約数)4番目の最小値となる式は3 ^ 2 +5 ^ 2 +7 ^ 2 +11 ^ 2 +17 ^ 2 +19 ^ 2 +23 ^ 2 =1383(≠素数　3が約数)5番目の最小値となる式は3 ^ 2 +5 ^ 2 +7 ^ 2 +13 ^ 2 +17 ^ 2 +19 ^ 2 +23 ^ 2 =1431(≠素数　3が約数)6番目の最小値となる式は3 ^ 2 +5 ^ 2 +11 ^ 2 +13 ^ 2 +17 ^ 2 +19 ^ 2 +23 ^ 2 =1503(≠素数　3が約数)7番目の最小値となる式は3 ^ 2 +7^ 2 +11 ^ 2 +13 ^ 2 +17 ^ 2 +19 ^ 2 +23 ^ 2 =1527(≠素数　3が約数)ということでどれも素数ではないので8番目の最小値の1543が最小の素数と確認できましたなちなみに検証した式は全て3が約数となっておりますがそれは証明が可能でございますな先に指摘した「大学の理系学部の演習問題」の証明の中の主張が適用できるケースとなりますな簡単に言うと3以外のすべての素数pについて　 p²≡1(mod.3)となるので3以外の「3の倍数となる個数の素数」の平方の和を考えるとp₁²+p₂²+p₃²+・・・・p²≡3n≡0(mod.3)となりますな。よって・・・3の平方と3以外の異なる6つの素数の平方の和（計７つの和）は必ず3が約数になりますな異なる8つの素数の2乗の和となる最小の素数は？15312 ^ 2 +3 ^ 2 +7 ^ 2 +11 ^ 2 +13 ^ 2 +17 ^ 2 +19 ^ 2 +23 ^ 2 =この式は5^2を抜いて、素数の中で9個番目に大きい23を追加したという形ですな最小値ではないですが他の最小値候補の件数は少ないのでまた検証してみましょう最小値となる式は2 ^ 2 +3 ^ 2 +5 ^ 2 +7 ^ 2 +11 ^ 2 +13 ^ 2 +17 ^ 2 +19 ^ 2 =1027(≠素数　13*79)2番目の最小値となる式は2 ^ 2 +3 ^ 2 +5 ^ 2 +7 ^ 2 +11 ^ 2 +13 ^ 2 +17 ^ 2 +23 ^ 2 =1195(≠素数　5が約数)3番目の最小値となる式は2 ^ 2 +3 ^ 2 +5 ^ 2 +7 ^ 2 +11 ^ 2 +13 ^ 2 +19 ^ 2 +23 ^ 2 =1267(≠素数　=7*181)4番目の最小値となる式は2 ^ 2 +3 ^ 2 +5 ^ 2 +7 ^ 2 +11 ^ 2 +17 ^ 2 +19 ^ 2 +23 ^ 2 =1387(≠素数　=19*73)5番目の最小値となる式は2 ^ 2 +3 ^ 2 +5 ^ 2 +7 ^ 2 +13 ^ 2 +17 ^ 2 +19 ^ 2 +23 ^ 2 =1435(≠素数　5が約数)6番目の最小値となる式は2 ^ 2 +3 ^ 2 +5 ^ 2 +11 ^ 2 +13 ^ 2 +17 ^ 2 +19 ^ 2 +23 ^ 2 =1507(≠素数　=11*137)ということで7番目の最小値の1531が最小の素数と確認できましたなちなみに8つの和の最小値の素数が、7つの和の最小値の素数よりも小さいという結果になるのですな・・・異なる9つの素数の2乗の和となる最小の素数は？23933 ^ 2 +5 ^ 2 +7 ^ 2 +11 ^ 2 +13 ^ 2 +17 ^ 2 +19 ^ 2 +23 ^ 2 +29 ^ 2 =この数字については前々回の記事で取り上げておりますなこの式も最小値であることは一目瞭然という形でございますな異なる10つの素数の2乗の和となる最小の素数は？38772 ^ 2 +5 ^ 2 +7 ^ 2 +11 ^ 2 +13 ^ 2 +17 ^ 2 +19 ^ 2 +23 ^ 2 +31 ^ 2 +37 ^ 2 =これは3^2と29^2を抜いてから31 ^ 2 と37 ^ 2を加えた10個となりますなちょっと簡単には最小値であると確認することは一見には難しいように見えますなですがプログラムによって組み合わせで考えられる式を元に値の小さい順から素数を探し出させた結果でございますので相違はありませんよまた7つのケースについて「大学の理系学部の演習問題」の主張の一部を用いて説明したことが10つのケースでも適用できますので最小値となる式は2^2を含める、かつ3^2を含めない形となりますなつまり2 ^ 2 +5 ^ 2 +7 ^ 2 +11 ^ 2 +13 ^ 2 +17 ^ 2 +19 ^ 2 +23 ^ 2 +29 ^ 2 +31 ^ 2 =が最小値でして3349となりますがこれは17*197 と素数ではありませんな答えとした3877はこの最小値式の次善となる最小値式ですので正しいということになりますなちなみに次の大きい素数は以下となりますよ43572 ^ 2 +5 ^ 2 +7 ^ 2 +11 ^ 2 +13 ^ 2 +17 ^ 2 +19 ^ 2 +23 ^ 2 +31 ^ 2 +43 ^ 2 =異なる11つの素数の2乗の和となる最小の素数は？47233 ^ 2 +5 ^ 2 +7 ^ 2 +11 ^ 2 +13 ^ 2 +17 ^ 2 +19 ^ 2 +23 ^ 2 +29 ^ 2 +31 ^ 2 +37 ^ 2 =この式は奇数個の和ですのでまず2^2を抜いて全て奇数だけにする必要がありますなその上で3からの連続する素数11個を並べた式ですので最小値であることは自明ですなこれが素数になるという結果ですのでなかなか興味深いですな異なる12つの素数の2乗の和となる最小の素数は？50392 ^ 2 +3 ^ 2 +5 ^ 2 +7 ^ 2 +11 ^ 2 +13 ^ 2 +17 ^ 2 +19 ^ 2 +23 ^ 2 +29 ^ 2 +31 ^ 2 +41 ^ 2 =これは12番目の素数37を抜いて13番目の素数41を追加した式ですので2番目の最小値となる式ですなちなみに最小となる式は以下でございますがこれは素数ではないですな2 ^ 2 +3 ^ 2 +5 ^ 2 +7 ^ 2 +11 ^ 2 +13 ^ 2 +17 ^ 2 +19 ^ 2 +23 ^ 2 +29 ^ 2 +31 ^ 2 +37 ^ 2 =4727(≠素数　=29*163)異なる13つの素数の2乗の和となる最小の素数は？104535 ^ 2 +7 ^ 2 +11 ^ 2 +13 ^ 2 +17 ^ 2 +19 ^ 2 +23 ^ 2 +29 ^ 2 +31 ^ 2 +37 ^ 2 +41 ^ 2 +43 ^ 2 +47 ^ 2 =この答えの計算に私のPCではちょっと時間がかかりましたよそれはさておきこの式は単純な話でいうと最小値の式ではないことになりますが素数となり得るかどうかを考慮して最小値となる和の式を考えてみますと・・・・13つと奇数個ですから2^2は必ず抜く必要がありますなさらに3^2を含めると残りは奇数素数が12つとなってその平方の和は必ず3が約数となってしまうので3^2も抜く必要がありますなつまり上記の式は素数の候補となる最小の式であるということになりますなそして実際に素数でありますよ5からの13個の素数を連続して並べた美しい形ですなこのような規則的に生成した式の値が素数であることにはちょっと驚きですないやただの偶然なのでしょうが不思議な結果でございますな世の中の不思議な現象というのはこういうただの偶然の結果なのだと考えるとなにが起きても全て納得するしかないような気がしますな

2022/02/02

コメント(0)