JINさんの陽蜂農遠日記

12321のように逆さから読んでも同じ数になる数を 回文数 といいます。
1桁の数から回文数を調べてみましょう。
1桁の数 は 0、1、2、3、4、5、6、7、8、9の10個 はすべて回文数になるのは当たり前です。
2桁の数 は 11、22、33、44、55、66、77、88、99の9個 です。
3桁の数 は1 01、111、121、131、141、151、161、171、181、191、202、212、222、
　　　　　232、242、252、262、272、282、292、…、909、919、929、939、949、
　　　　　959、969、979、989、999です。100の位から900の位までそれぞれ10個ずつ
　　　　　あるので90個 です。
4桁の数 は 1001、1111、1221、1331、1441、1551、1661、1771、1881、1991という
　　　　  ように 1000から2000までの中に10個 あります。3桁の数の場合と同じです。
　　　　  よって、 9999までの中に10×9＝90個 あることになります。

【回文数 】 の中で素数であるものを【回分素数】と呼びます。
回文数の中から回文素数を探してみましょう。
1桁の回文素数は2、3、5、7です。
2桁の回文素数は11だけです。
3桁の回文素数は101、131、151、181、191、313、353、373、727、757、787、797、
                       919,929の14個です。
このような回文素数には次の基本的性質があります。偶数個の数字からなる回文素数は
2個の数字からなる11が唯一である。
それは、偶数個の数字からなる回文数はすべて11で割り切れるからです。
2個の数字からなる
回文数11、22、33、44、55、66、77、88、99は11で割り切れますし、
4個の数字からなる
回文数1001、1111、1221、1331、1441、1551、1661、1771、1881、1991、…も
確かにすべて11で割り切れます。

【回分素数】が無数に存在するかどうかは分かっていない 2021年8月時点で知られている
最大の【回分素数】は 10＾490000 + 3 · (10＾7383 - 1)/9 · 10＾241309 + 1である

全ての整数が高々3つの回文数の和で表せることがアルゴリズムとともに示されています。
0も回文数に含んでいるので自明な組は多いのですが、
例えば23805であれば
  21012
    2662
+    131

   23805

のように3つの回文数の和で表せます。

「リクレル数」と「196問題」

ただしこれは一般的な名称ではないので注意して下さい。
ある整数に対して、自身とその逆順数との和を求める操作のことを「リクレルプロセス」と
呼びます。
例えば、56なら
56+65＝121となり、125なら
125+521＝646
となります。これが１回の リクレルプロセス に相当します。
多くの数は リクレルプロセス を繰り返し適用すると、いずれは 回文数 になります。
特に、1桁と2桁の数字は全て、リクレルプロセスを繰り返すと最終的に 回文数 になることが
知られています。
「 89 」が回文数になるまでは、 ２４回の操作 が必要である。実際に、演算結果のみ示すと、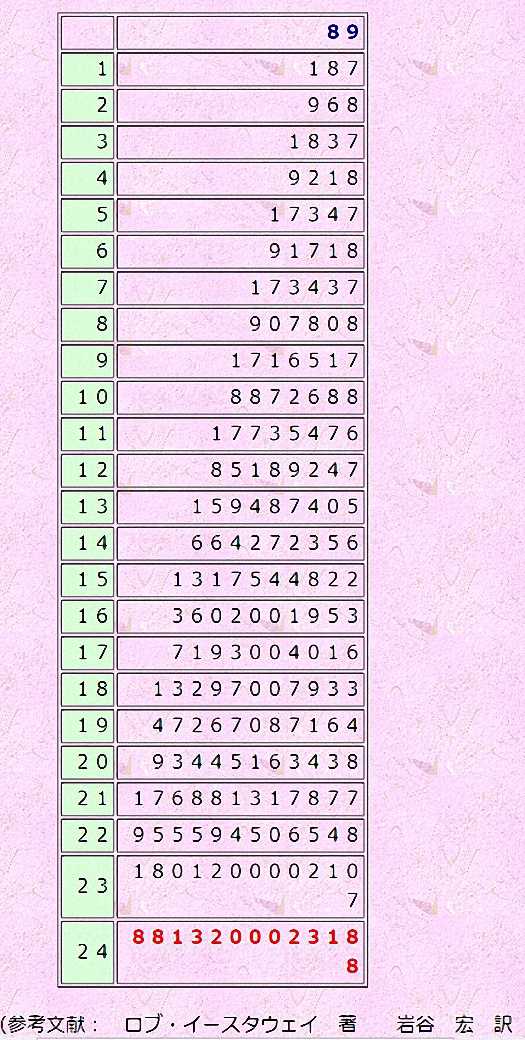



ここで、 何回リクレルプロセスを繰り返しても回文数にならない整数のことを「リクレル数」 と
呼びます。しかしこれはあくまでも定義でしかなく、十進数における
リクレル数の存在は証明されていません。
つまり 「十進数のリクレル数は存在するのか？」という問いは数学の未解決問題 なのです。
十進数の場合は証明ができていないだけで、リクレル数の候補は幾つか知られています。
例えば、 196 などはリクレル数であると予想されています。
196,295,394,493,592,689,691,788,790,879,887,978,986
十進数におけるは最小のリクレル数の候補であるため、リクレル数か否かについて特に
注目されています。 196 がリクレル数か否かを判断する問題には「 196問題 」と特別に
名前が付けられています。 数十億回の反復後でも未だに回文は得られていない ようです。

                                                                                        ・・・​ もどる ​・・・


　　　　　　　　　　　　　　　　　　・・・​ つづく ​・・・