問題2
図1に示すような長期鉛直荷重を受けるブレース付き鉄骨造門型骨組の柱の座屈等に関する次の設問に解答せよ。なお、圧縮材の座屈の長期許容応力度 fc は式(1)によるものとし、ブレースは圧縮力に対しても抵抗すると考える。柱及び梁は十分に横補剛されており、構面外座屈はしないものとする。各部材の断面形状及び材料特性は表1のとおりで、断面性能は表1の値を用いることとする。
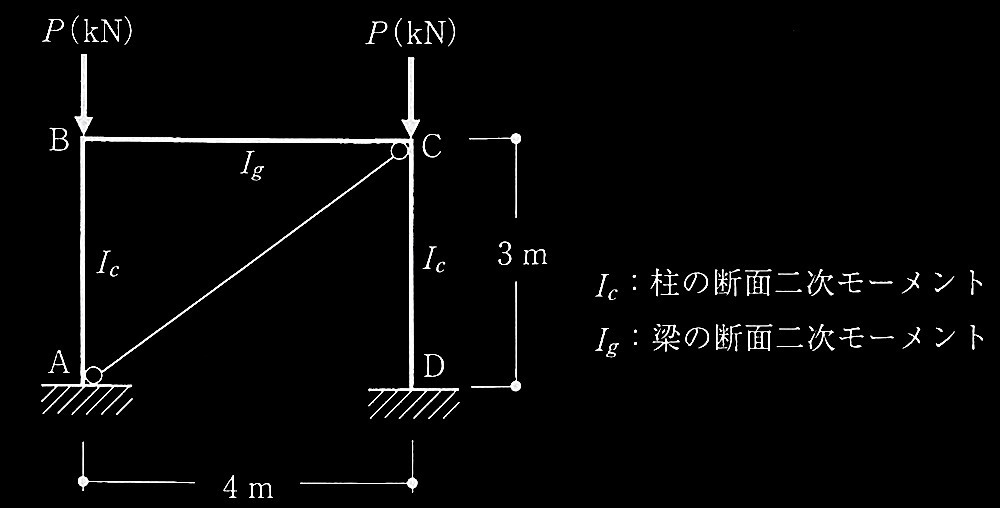
図1 ブレース付き門型骨組
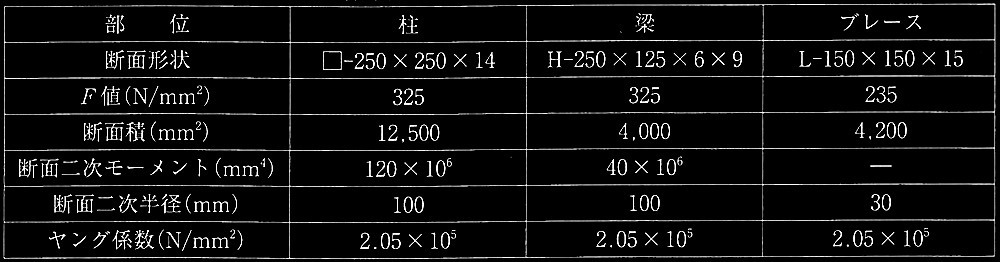
表1 各部材の断面形状・材料特性・断面性能

[ No.1 ]
本骨組において、柱が表1に示す角形鋼管、梁が剛体とみなせる場合について、以下の設問に解答せよ。
?@ 両端固定で節点の水平移動がないものとして、柱の座屈長さを求めよ。
答え
両端固定で接点の水平移動がない場合の柱の座屈長さは、
?k = 0.5 × ?c(柱の長さ) = 0.5 × 3.00m = 1.50m
となる。
?A 柱の長期許容圧縮応力度を求めよ。
答え
柱の長期許容圧縮度は
λ = 1500mm / 100mm(断面二次半径) = 15.0
Λ = 1500/ ( √325N/mm 2
(F値) / 1.5) = 102
λ ≦ Λより
長期許容圧縮応力度
fc = F × { 1 − 2/5 × (λ/ A) 2
} / {3/2 + 2/3 × (λ / Λ) 2
}
= 325× { 1 − 2/5 × (15/102) 2
}/{3/2 + 2/3 × (15/102) 2
}
= 213 N/mm 2
となる。
鋼材のF値:
基準強度 単位 N/mm 2
「降伏点の値と引張強さの70%のうち小さい方」と定義される設計用の数値であるが、通常の鋼材では降伏点の値となる。
鋼材の許容応力度:
長期 引張・圧縮・曲げ F/1.5
せん断 F/1.5√3
短期 長期に対する値の1.5倍
?B 柱1本の長期許容圧縮力を求めよ。
答え
柱1本の長期許容圧縮力は
N ac
= 12500mm 2
(断面積) × 213 N/mm 2
(長期許容圧縮応力度)
= 2660kN
となる。
※有効数字3桁とした
[ No.2 ]
本骨組において、柱が表1に示す角形鋼管、梁が表1に示すH形鋼の場合について、以下の設問に解答せよ。
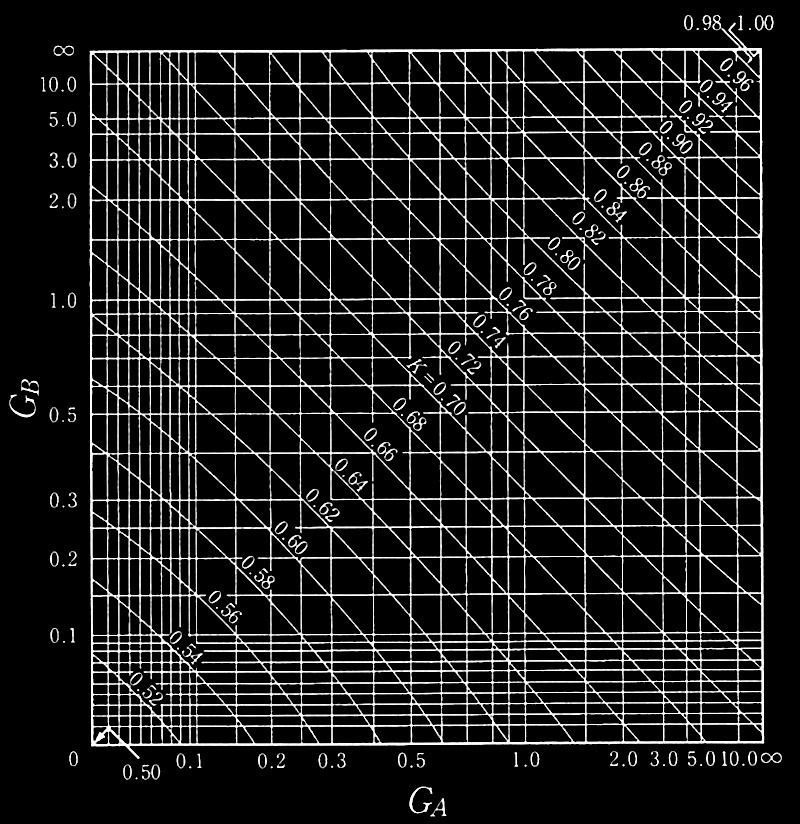
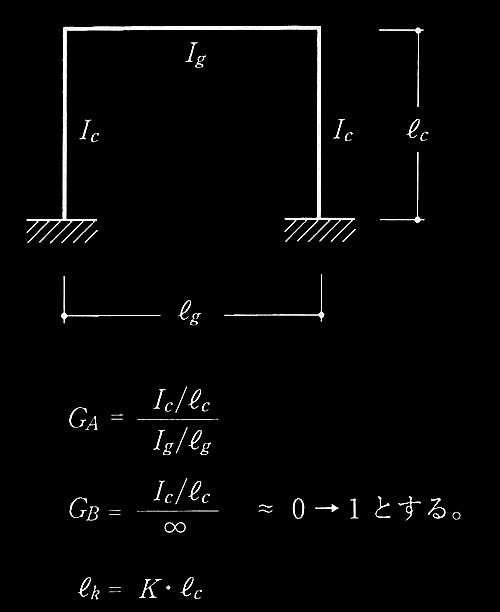
図2 柱頭の水平移動が拘束される場合の座屈長さ係数Kの算定図
(引用:日本建築学会「鋼構造座屈設計指針」(一部編集))
?@ 図2を用いて座屈長さ係数 Kを求める場合のG A 値を求めよ。
答え
G A
は
( Ic /?c) / ( lg /?g)
= (120 × 10 6
mm 4
/3000mm) / (40X10 6
mm 4
/4000mm)
= 4.00
となる。
?A 図2を用いて座屈長さ係数 Kの値を求めよ。なお、G B = 1とする。
答え
座屈長さ係数 Kは、G A
=4.00、G B
=1.0より下図から 0.840となる。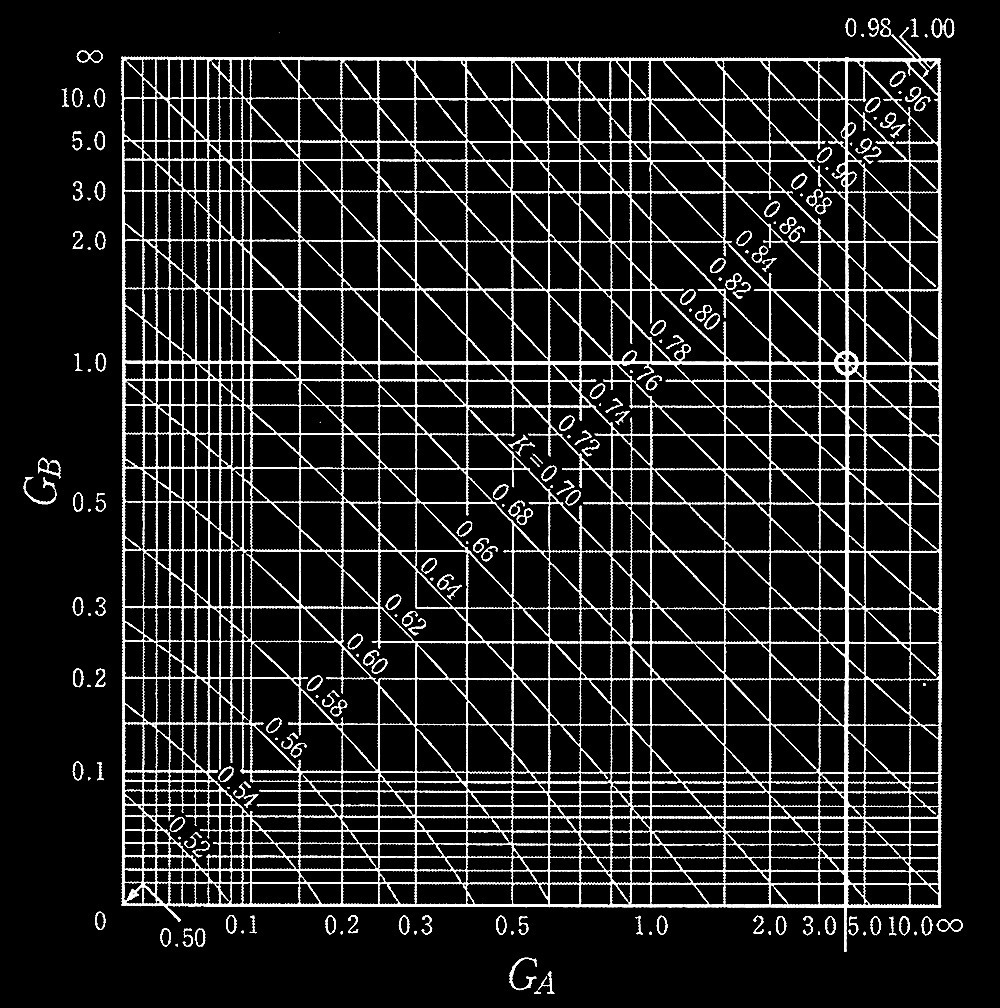
?B 座屈長さ係数Kを用いた柱の座屈長さを求めよ。
答え
柱の座屈長さ?kは
?k = K × ?c = 0.840 x 3000mm = 2520mm
となる。
?C 柱の長期許容圧縮応力度を求めよ。
答え
柱の長期許容応力度は
λ = 2520mm/100mm(断面二次半径)=25.2
Λ = 102
λ ≦ Λ
より
長期許容圧縮応力度
fc = F × {1-2/5 × ( λ/Λ) 2
} / {3/2 + 2/3 × (λ/Λ) 2
}
= 325× {1-2/5 × (25.2/102) 2
} / {3/2+ 2/3 × (25.2/102) 2
}
= 206 N/mm 2
となる。
?D 柱1本の長期許容圧縮力を求めよ。
答え
柱1本の長期許容圧縮力は
N ae
= 12500mm 2
(断面積) × 206N/mm 2
(長期許容圧縮応力度)
= 2580kN
となる。
※有効数字3桁とした
[ No.3 ]
本骨組において、ブレースが表1に示す等辺山形鋼の場合について、以下の設問に解答せよ。
?@ ブレースの長期許容圧縮力を求めよ。
答え
ブレースの長期許容圧縮力は、両端ピンとして母材断面で求めると
ブレース長さ
?v = √ (3m 2
+ 4m 2
)
= 5.0mm→5000mm
ブレースの座屈長さ
?k = 1.0 × 5000mm = 5000mm(両端ヒ°ン)
λ= 5000mm/ 30mm(断面二次半径)=167
Λ = 1500 / (√ 235N/mm 2
(F値)/1.5) =120
λ> Λより
長期許容圧縮応力度 fc = (18/65)/(λ/Λ) 2
× F
= (18/65)/(167/120) 2
× 235 N/mm 2
= 33.6 N/mm 2
ブレースの長期許容圧縮力
N ac
= A × fc = 4200 mm 2
× 33.6N/mm 2
= 141kN
となる。
?A [ No.2 ]の場合について、ブレースが柱頭の水平移動を拘束できるか否かを検討せよ。なお、ブレースが負担する水平力は、柱2本の長期許容圧縮力の2%とする。
答え
ブレースが負担する水平力は、No.2における柱の長期許容圧縮力Nac=2580kNの2本分に対して2%となるため、
2580kN × 2 × 0.02 = 103kNとなる。
この際のブレースの軸力Nは、
N= 103kN × (5.0m/ 4.0m)= 129kNとなり、ブレースの長期許容圧縮力Nac = 141kN以内であるため、
ブレースは柱頭の水平移動を拘束可能である
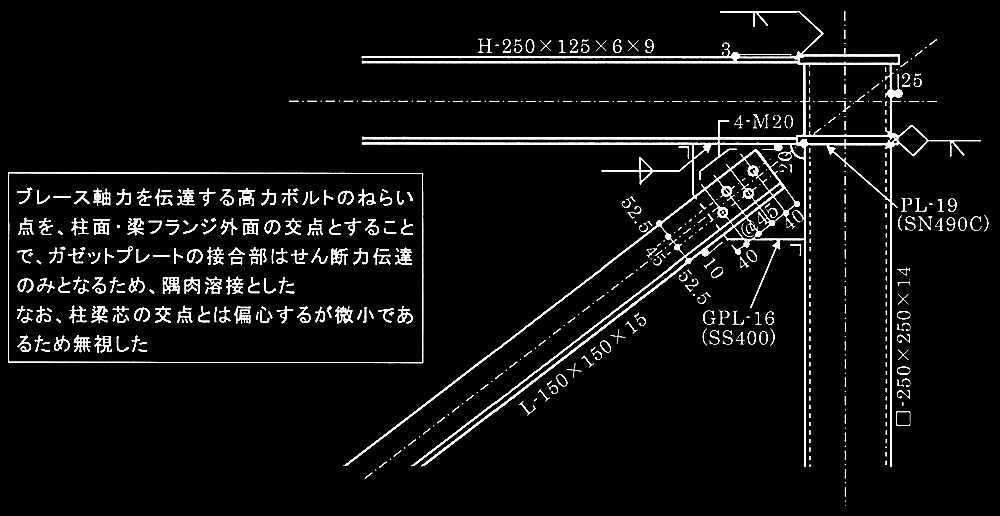
?B [ No.2 ]の場合について、節点Cにおけるブレースと柱梁接合部の納まりをスケッチせよ。使用するボルトは、M20(F10T)とし、1本当たりの1面摩擦に対する長期許容せん断力は、46.2 kNとする。
答え
ブレースは柱頭の水平移動を拘束するためにのみ働くものとし、ブレースの長期許容圧縮力
N ac
= 141kNに対して安全であるおさまりとする。
必要なボルト本数は、141kN/46.2kN= 3.05より4本とすると、収まりは以下となる。