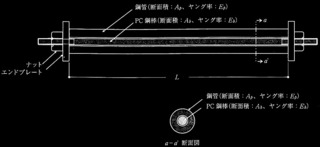
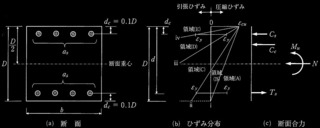
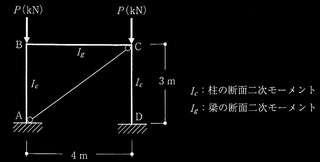
問題3
免震ピットの立上り壁に作用する偏土圧に関する設問 [ No.1 ]、及び建築物の直接基礎(べた基礎)の設計に関する設問[ No.2 ]に解答せよ。
[ No.1 ]
図1に示すような免震ピットの立上り壁に作用する土圧及び水圧に関する以下の?@及び?Aの設問に解答せよ。ただし、土の単位体積重量γは18 kN/m 3 、水の単位体積重量は10 kN/m 3 とし、地表面に作用する上載荷重 q は10kN/m 2 とする。
なお、地表面からの深さzの位置の土圧 p z は式(1)により求めるものとする。
p z = K (q + σ z ) (kN/m 2 ) 式(1)
ここに、
K:土圧係数
σ z :深さzの位置の上載荷重を除いた土圧で、σ z =γ•z(kN/m 2 )。
ただし、地下水位以深のγは水中単位体積重量を用いる。
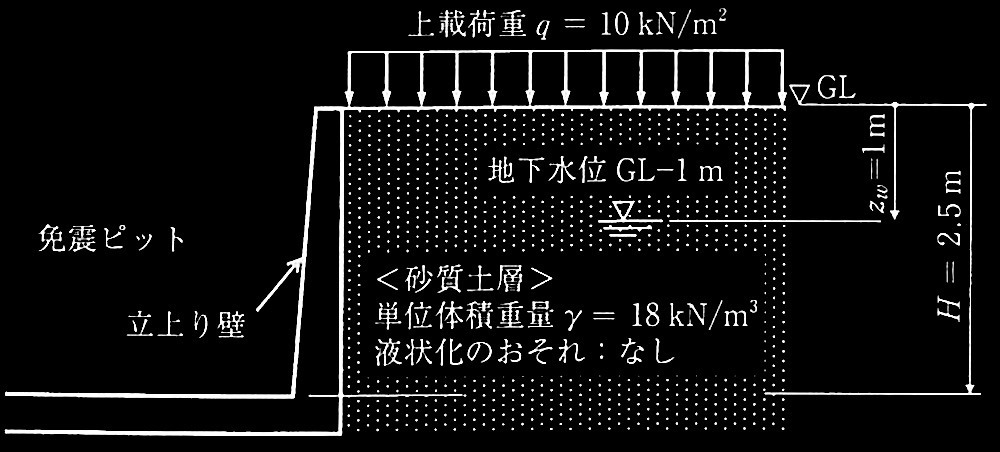
図1 土圧及び水圧が作用する免震ピットの立上り壁
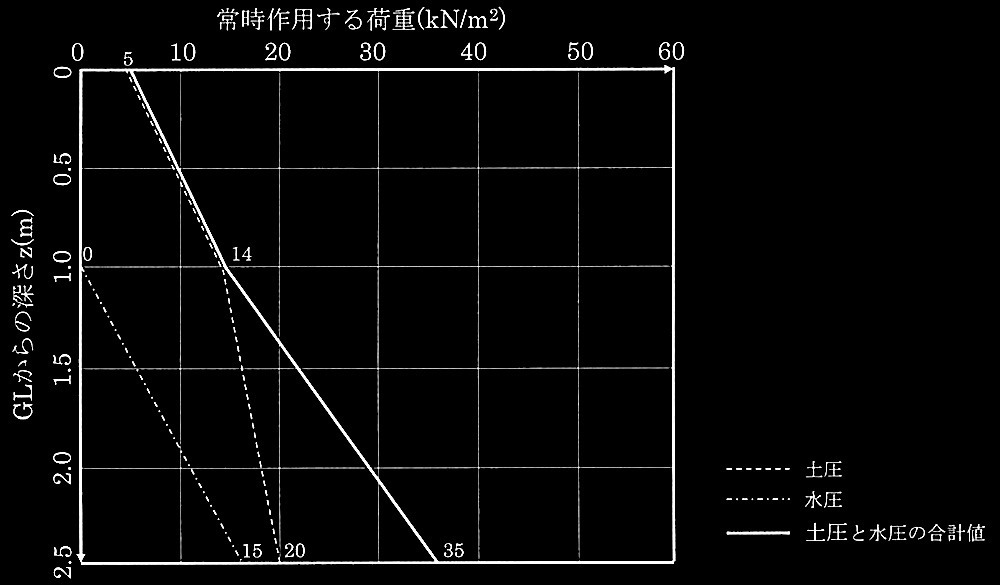
?@ 常時作用する土圧、水圧、及び「土圧と水圧の合計」を算定して、答案用紙のグラフ?@にそれぞれの深さ方向の分布を記入せよ。ただし、土圧は破線、水圧は一点鎖線、「土圧と水圧の合計」は実線で示すこと。それぞれの線には、深さ0m(地表面)、1.0m(地下水位点)及び2.5m(壁脚部)での土圧•水圧の値を記入すること。なお、常時作用する土圧は静止土圧で、静止土圧係数 Koは0.5とし、水圧は静水圧とする。
次に、立上り壁脚部の幅1mあたりに常時作用するせん断力Q L (kN/m)を求めよ。
答え
式(1) から土圧p z
は
p z
= K( q + σ z
)
で示され、各項目は下記による。
K = K o
= 0.5
q = 10 (kN/m 2
)
σ z
= γ•z
(地下水位以深いの場合は水中単位体積重量 18 – 10 = 8 kN/m 3
を用いる)
(a) 土圧p z
(z=0.0m):
p z
= Ko(q + γ•z )= 0.5(10kN/m 2
+ 0 ) = 5 kN/m 2
(z=1.0m):
p z
= Ko(q + γ•z )= 0.5(10kN/m 2
+ 18 kN/m3 × 1m ) = 14 kN/m 2
(z=2.5m):
p z
= Ko(q + γ•z )= 0.5(10kN/m 2
+ 18 kN/m3 × 1m + 8 kN/m3 ×1.5m) = 20 kN/m 2
(地下水位以深いの場合は水中単位体積重量 18 – 10 = 8 kN/m 3
を用いる)
(b) 水圧p w
(z=0.0m):
p w
= 0 kN/m 2
(z=1.0m):
p w
= 0 kN/m 2
(z=2.5m):
p w
= 1.0 × 10kN/m 3
× 1.5m=15kN/m 2
(c) 土圧と水圧の合計 p z
+ p w
(z=0.0m):
p z
+p w
= 5 + 0 = 5kN/m 2
(z=1.0m):
p z
+p w
= 14 + 0 = 14kN/m 2
(z=2.5m):
p z
+p w
= 20+15 = 35kN/m 2
(a) 〜(c)より、グラフにすると下図に示す通りとなる。
常時作用する荷重(kN/m 2
)
立上り壁脚部の幅1m当たりに常時作用するせん断力Q L
(kN/m)は下図に示すせん断力図より、
Q L
= ( 5kN/m 2
+ 14kN/m 2
) × 1.0m/2+ (14kN/m 2
+ 35kN/m 2
) × 1.5m/2
= 9.5+ 36.75 = 46.25kN/m → 46.3kN/m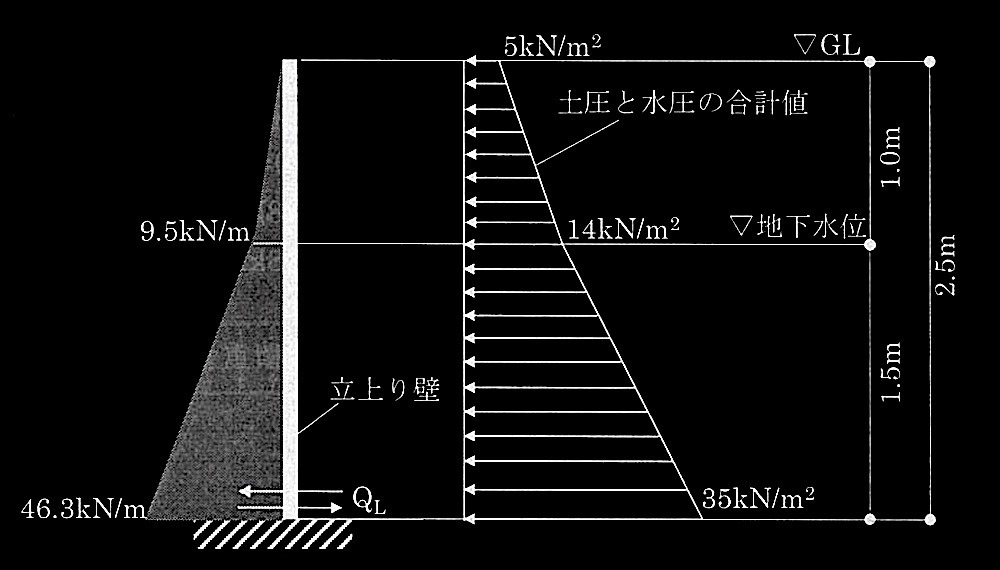
立上り壁のせん断力図
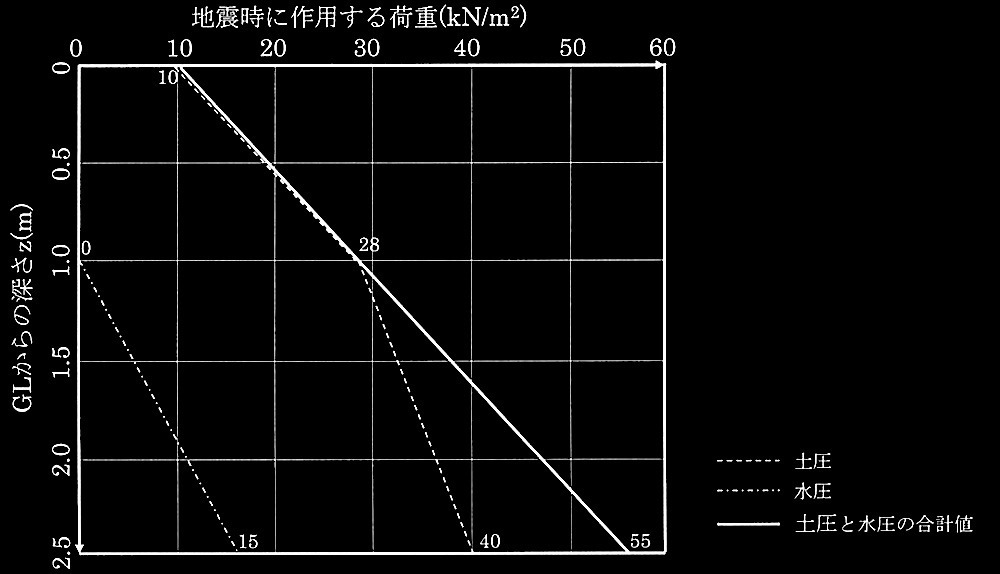
?A 地震時に作用する土圧、水圧、及び「土圧と水圧の合計」を算定して、答案用紙のグラフ?Aにそれぞれの深さ方向の分布を記入せよ。ただし、土圧は破線、水圧は一点鎖線、「土圧と水圧の合計」は実線で示すこと。それぞれの線には、深さ0m(地表面)、1.0 m(地下水位点)及び2.5m(壁脚部)での土圧•水圧の値を記入すること。なお、地盤は液状化しないものとし、極めて稀に発生する地震動を想定して、地震時土圧係数 K EA は1.0とし、水圧は静水圧とする。
答え
式(1) から土圧P z
は
p z
= K(q + σ z
)で示され、各項は下記による。
K = K EA
= 1.0
q = 10 (kN/m 2
)
σ z
= γ•z
(地下水位以深の場合は水中単位体積重量 18 −10= 8kN/m 3
を用いる)
(a) 土圧 p z
(z = 0.0m):
p z
= K EA
( q + γ’•z ) = 1.0 (10kN/m 2
+ 0) = 10kN/m 2
(z = 1.0m):
p z
= K EA
( q + γ’•z ) = 1.0 (10kN/m 2
+ 18kN/m 3
× 1m) = 28kN/m 2
(z = 2.5m):
p z
= K EA
( q + γ’•z ) = 1.0 (10kN/m 2
+ 18kN/m 3
× 1m + 8kN/m 3
× 1.5m)
= 40kN/m 2
(地下水位以深の場合は水中単位体積重量18-10 = 8kN/m 3
を用いる)
(b) 水圧P w
(z = 0.0m):
p w
=0kN/m 2
(z = 1.0m):
p w
=0kN/m 2
(z = 2.5m):
p w
=1.0 × 10kN/m 3
× 1.5m = 15kN/m 2
(c) 土圧と水圧の合計 p z
+ p w
(z = 0.0m):
p z
+ p w
= 10 + 0 = 10kN/m 2
(z = 1.0m):
p z
+ p w
= 28 + 0 = 28kN/m 2
(z = 2.5m):
p z
+ p was
= 40 +15 = 55kN/m 2
(a)〜(c)より、グラフにすると下図に示す通りとなる。
地震時に作用する荷重(kN/m 2
)
[ No.2 ]
建築物の基礎形式に直接基礎(べた基礎)を採用し、GL–2m以深に現れる砂質土層を支持層と想定して、以下のような条件を設定した。次の?@〜?Cの設問に解答せよ。
く基礎形式>
直接基礎(べた基礎:基礎底面B × L = 10 m × 20 m)
基礎の平均鉛直荷重度:50 kN/m 2
く基礎荷重状況と地盤概要> 図2参照
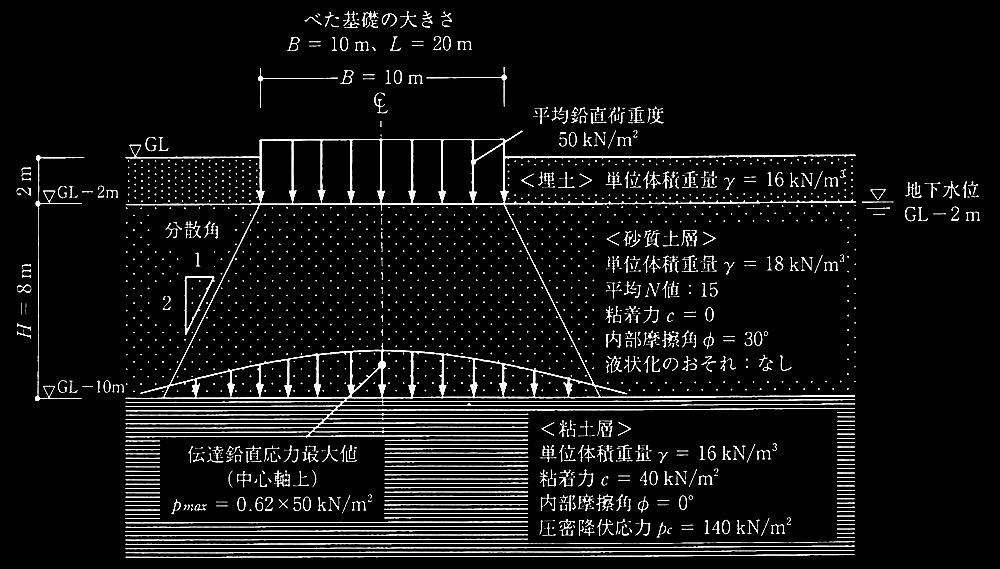
図2 基礎荷重状況と地盤概要
?@ 基礎直下の砂質土層の長期許容鉛直支持力度q α1 を、式(2)を用いて求めよ。ただし、根入れ深さD f には埋土部分は含まれないものとする。

表 支持力係数

答え
※数字の有効数字について、答えは3桁で表し、途中の計算も3桁で行った。最終桁の丸め方は四捨五入している。
基礎の形状係数:
α= 1.0 + 0.2•B/L =1.0 + 0.2•10/20 = 1.1
基礎の形状係数:
β = 0.5 – 0.2•B/L = 0.5 - 0.2•10/20 = 0.4
支持力係数(φ = 30°):
N c
= 30.1、N γ
= 15.7、N q
= 18.4
支持地盤の粘着力:
c = 0
支持地盤の単位体積重量:
γ 1
= 18 - 10 = 8 (kN/m 3
)
(地下水位以下のため水中単位体積重量)
根入れ部分の土の単位体積重量:
γ 2
= 16 (kN/m 3
)
根入れ深さ:
D f
= 0(m) (埋土は考慮しないため)
以上より、基礎直下の砂質土層の長期許容鉛直支持力度q α1
は式(2)より以下となる。
q α1
= (α•c•N c
+ β•γ 1
•B•N γ
+ γ 2
•D f
•N q
) /3
= (1.1• 0• 30.1 + 0.4•8•10•15.7 + 16•0•18.4) = 167 (kN/m 2
)
?A 直接基礎底面(GL −2m) に作用する鉛直荷重が、分散角1/2で粘土層表面(GL-10m)に ( B + H )•( L + H )の大きさに均等に載荷されるものとして、直接基礎底面 ( GL–2m )に換算した粘土層の長期許容鉛直支持力度q α2 を、式(3)を用いて求めよ。ただし、根入れ深さD f は砂質土層厚Hとし、埋土部分は根入れ深さに含まれないものとする。

答え
基礎の形状係数:
α= 1.0 + 0.2•(B + H)/(L + H) = 1.0 + 0.2•(10 + 8 )/( 20 + 8 ) = 1.13
基礎の形状係数:
β= 0.5 − 0.2•(B + H)/(L + H) = 0.5 – 0.2•(10 + 8 )/( 20 + 8 ) = 0.371
支持力係数(φ =0°) :
N c
= 5.1、N γ
= 0.0、N q
= 1.0
粘土層の粘着力:
c = 40 (kN/m 2
)
粘土層の単位体積重量:
γ 1
= 16 – 10 = 6 (kN/m 3
)
(地下水位以下のため水中単位体積重量)
根入れ部分(砂質土) の土の単位体積重量:
γ 2
=18 – 10 = 8 (kN/m 3
)
(地下水位以下のため水中単位体積重量)
根入れ深さ :
D f
= H = 8(m)
以上より、直接基礎底面(GL-2m)に換算した粘土層の長期許容支持力度q α2
は式(3)より以下となる。
q α2
=1/3 × (B + H)•(L + H)/B•L× { α•c•Nc + β•γ 1
•(B + H) •N γ
+ γ 2
•D f
•N q
}
=1/3 × (10+8)•(20+8)/10•20 ×(1.13•40•5.1 + 0.371•6•(10 + 8)• 0.0 + 8 •8 •1.0)
= 247 (kN/m 2
)
く参考>
2層地盤の検討を学会基礎指針2019(以下、基礎指針)に準拠して算出する。その概念図を下図に示す。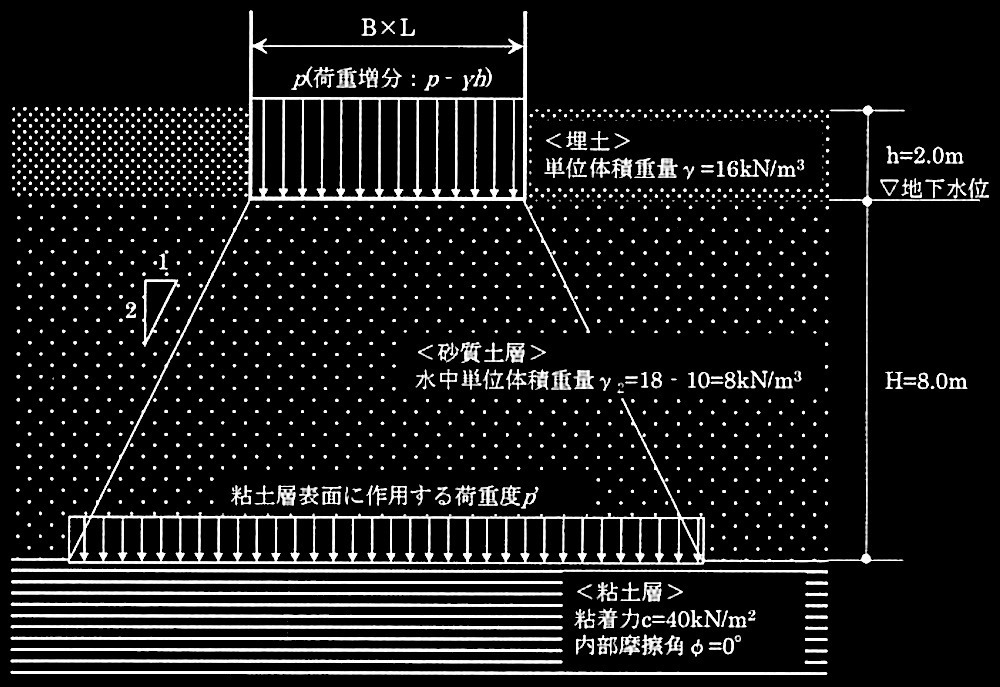
2層地盤の概念図
粘土層の極限支持力q’ u2
は基礎指針(5.2.2)式に準拠して下記のように示される。
ここで、埋土の単位体積重量をγ (=16kN/m 3
)、埋土の高さをh(=2.0m)とした。
q' u2
= a•c•Nc+β•γ 1
• (B + H)•N γ
+ (γ•h + γ 2
•H)•N q
= 1.13•40•5.1 + 0.371•6 •(10 + 8)•0.0 + (0 + γ2•H) •1.0
= 230.5 + γ 2
•H (kN/m 2
)
(極限支持力算定時には安全側となるように埋土の根入れ効果分のγ•hは無視した。)
根入れ底面に作用する荷重増分(p – γ•h)により、粘土層表面に作用する荷重度 p' は基礎指針(5.2.22)式に準拠して下記で示される。
p’ = B•L/{(B+H)•(L+H)} × (p – γ• h) + γ•h + γ 2
•H
ここで、p'= q' u2
として、pを求める。
B•L/{(B+H)•(L+H)} × (p – γ• h) + γ•h + γ 2
•H = 230.5 + γ 2
•H
p = (B+H)•(L+H) /B•L × (230.5 − γ•h) + γ•h
= (10+8)•(20+8)/10•20 × (230.5 − 16•2.0) + 16•2.0 = 532 (kN/m 2
)
以上より、q α2
=p/3で示されるため、q α2
は以下となる。
q α2
=p/3 = 532/3 = 177 (kN/m 2
)
?B 圧密沈下が発生するか否かを計算で求めよ。ただし、基礎の鉛直荷重度による粘土層の上面 ( GL-10m ) の中心軸上の伝達鉛直応力の最大値P max は、図2に示すように 0.62 × 50 kN/m 2 とする。圧密沈下の検討では埋土の重量も考慮するものとする。
答え
粘土層に作用する最大荷重 p d
と粘土層の圧密降伏応力 p c
の比較を以下に行う。
埋土の重量:
w b
= γ•2=16 × 2 = 32.0 (kN/m 2
)
砂質土層の重量 :
w s
= (γー10)•H = (18 – 10)• 8 = 64.0 (kN/m 2
)
伝達鉛直応力の最大値 :
p max
= 0.62 × (50 - 32) = 11.2 (kN/m 2
)
ここでは、基礎の平均鉛直荷重度 50 kN/m 2
は、接地圧(建物荷重)と考え、荷重増分は接地圧から埋土重量γ•hを減じている。また、粘土層にかかる最大荷重を求める際、周辺の粘土層からの影響係数が示されていないことからw b
に最大値を採用する。
粘土層にかかる最大荷重:
p d
= w b
+ w s
+ p max
= 32.0 + 64.0 + 11.2 = 107 (kN/m 2
)
< P c
= 140 (kN/m 2
)
以上より、粘土層にかかる最大荷重 p d
は107kN/m 2
であり、粘土層の圧密降伏応力 p c
= 140kN/m 2
未満であるため、圧密沈下は発生しない。
?C 以上の?@〜?Bの検討より、図2に示すような直接基礎(べた基礎)で設計することが可能か否かを判断せよ。あわせて、その理由を述べよ。
答え
以下の理由により、基礎の構造安全性に問題はなく、直接基礎(べた基礎)で設計することは可能である。
・?@の結果より、基礎直下の砂質土層の長期許容鉛直支持力度q α1
は167kN/m 2
であり、基礎の平均鉛直荷重度50kN/m 2
は砂質土層の長期許容鉛直支持力度以下であるため。
・?Aの結果より、直接基礎底面(GL−2m)に換算した粘土層の長期許容支持力度q α2
は247kN/m 2
であり、基礎の平均鉛直荷重度50kN/m 2
は、粘土層の長期許容鉛直支持力度以下であるため。
・?Bの結果より、粘土層にかかる最大荷重 p d
= 107kN/m 2
は、粘土層の圧密降伏応力p c
=140kN/m 2
未満であり、圧密沈下は発生しないため。