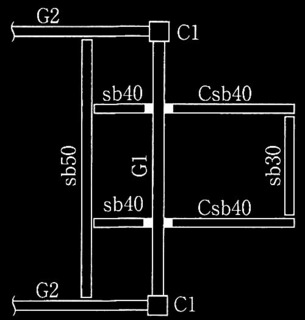
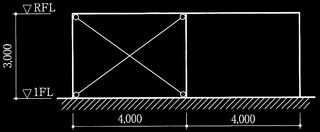
問題2
耐震計算ルート3により、異なる3つの鉄筋コンクリート造建築物を対象に静的弾塑性荷重増分解析(以下、「増分解析」という)を実施して、保有水平耐力を確認した。
次の [ No.1 ]〜[ No.3 ] の設問に解答せよ。なお、各層の層間変形角の最大値をR max と呼ぶ。
[ No.1 ]
計算対象の建築物は、5階建て鉄筋コンクリート耐力壁付きラーメン構造である。増分解析による保有水平耐力の計算に用いた条件及び計算結果等を以下に示す。
・架構は増分解析時に脆性破壊することなく、R max が1/60時点において全体崩壊形を形成した。
・架構の水平耐力はR max が1/100時点において必要保有水平耐力を上回っていた。
・R max が 1/100時点及び 1/60時点における1階の柱•耐力壁の種別ごとの負担水平力の和及び層せん断力を表1に示す。なお、表1に示す柱及び耐力壁の種別は、R max が 1/100時点、あるいは 1/60時点における応力等によりそれぞれ求めた。表1に示す以外の種別の柱及び耐力壁はなかった。
表1 1階の柱•耐力壁の種別ごとの負担水平力の和及び層せん断力
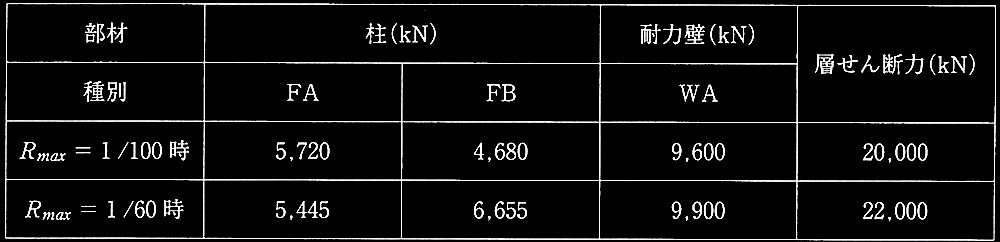
以上の条件及び計算結果を基に、必要保有水平耐力を算定するための次の?@及び?Aの設問に解答せよ。
?@ 1階の構造特性係数Dsの算出に用いる 柱の部材群としての種別を告示に従って判定し、その判定理由を簡潔に記述せよ。
答え
[ 解答解説 ]
全体崩壊形を形成したR max=1/60時を崩壊形とし、各部材の負担水平力から柱の部材群としての種別を判定する。
・部材の耐力の割合の算定
γ A
= 5,445/(5,445 + 6,655) = 0.45
γ C
= 0/(5,445 + 6,655) = 0.00
・部材群の種別の判定
次の表により判定する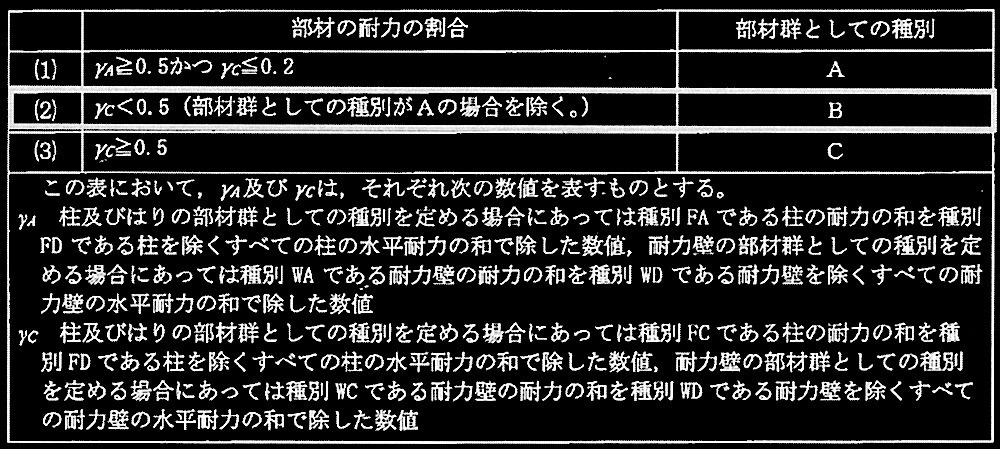
γ A
く0.5であることから部材群としての種別はAではない。
γ C
< 0.5であり、部材群としての種別はAでないことから、部材群としての種別はBの条件にあてはまる。
→ 部材群としての種別はB
?A 1階の構造特性係数Dsを告示に従って算出し、その算出理由を簡潔に記述せよ。
答え
[ 解答解説 ]
全体崩壊形を形成したR max
=1/60時を崩壊形とし、各部材の負担水平力から柱の部材群としての種別を判定する。
・β u
の算定
β u
= 9,900 / 22,000 = 0.45
・Dsの判定
次の表により判定する。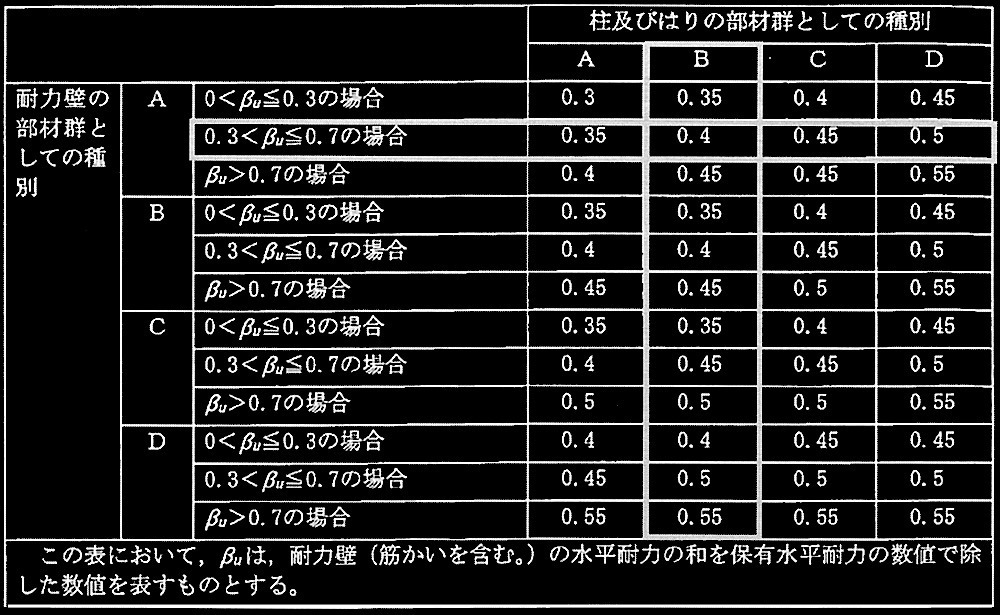
柱の部材群としての種別:B
耐力壁の部材群としての種別:A
β u
= 0.45
であることから、 Ds = 0.40となる
[ No.2 ]
計算対象の建築物は6階建て鉄筋コンクリート連層耐力壁付きラーメン構造である。次の枠内の文章は、増分解析に用いた条件及び増分解析結果の経過を述べたものである。
・せん断破壊した耐力壁は負担水平力を保持するとみなして、増分解析を行う。
・2階の構造特性係数Dsは鉄筋コンクリート構造の最大値である0.55として、必要保有水平耐力を計算する。
く増分解析結果の経過>
・R max が 1/250時点において、2階の連層耐力壁の一つが最初にせん断破壊した。
・R max が 1/200時点において、2階の連層耐力壁の過半(耐力壁の負担せん断力の合計が層せん断力の50%以上)がせん断破壊した。
・R max が 1/170時点において、2階の連層耐力壁の過半(耐力壁の負担せん断力の合計が層せん断力の70%以上)がせん断破壊した。
・R max が 1/100時点において解析を終了した。解析終了時には、全ての連層耐力壁がせん断破壊、あるいは曲げ破壊した。
以上の経過を基に、2階の保有水平耐力として、 R max がどの時点の層せん断力を採用するのが適切か、その理由も含めて簡潔に記述せよ。
答え
[ 解答解説 ]
R maxが1/250時点の層せん断力を採用するのが適切。
理由は以下の通り。
・耐力壁はせん断破壊後に構造耐力上支障のある急激な耐力低下を起こすことから、Rmax=1/250時点より変形が進むと、架構は耐力を維持できる状態でなくなっている。
・上記より、以降のそれ以降の解析で得られた層せん断力は実際の架構の耐力を反映できていない。
[ No.3 ]
計算対象の建築物は8階建て鉄筋コンクリートラーメン構造である。増分解析に用いた条件・仮定及び計算結果を以下に示す。
・使用した増分解析プログラムでは、N ≧ 0.4bDFc のときの1階外柱の曲げ終局モーメント(Mu)の算定式として、式(1)が用いられている。

く計算結果>
・荷重の増大にともない1階外柱の柱脚に塑性ヒンジが発生し、その後、柱脚の曲げ終局モーメントが最大になり、脆性破壊することなく、R max が 1/40時点において全体崩壊形を形成した。
・全体崩壊形が形成されるまで、柱脚には塑性ヒンジが生じた状態が継続され、柱頭には塑性ヒンジは生じなかった。
・1階外柱の曲げ終局モーメントが最大になった時点(ステップA)及び全体崩壊形の形成時点(ステップB)における1階外柱のモーメントを図1及び表2に示す。図1及び表2中の記号は式(1)と同じである。
・ここでは、柱頭の曲げモーメントは、柱脚に塑性ヒンジが発生した後は一定としている。
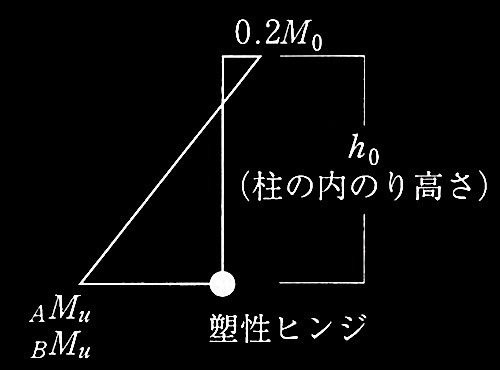
図1 1階外柱の曲げモーメント
表2 ステップA及びステップBの1階外柱の応力表
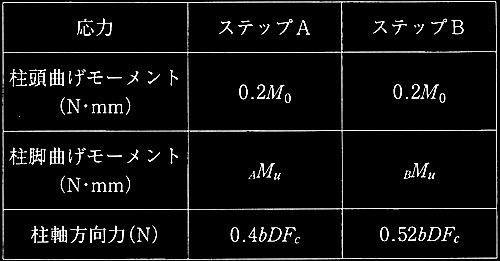
以上の条件・仮定及び計算結果を基に、1階外柱に関する以下の?@〜?Bの設問に解答せよ。
?@ ステップBにおける柱のせん断力(Q B )を、M 0 及び h 0 を用いて表記せよ。
答え
[ 解答解説 ]
・ B
Muの算定
B
Mu = M o
× (bDFc − 0.52bDFc)/(bDFc − 0.4bDFc) = 0.8 Mo
・Q B
の算定
Q B
= (0.2Mo + BMu) /ho = (0.2Mo + 0.8Mo)/ho= Mo/ho
?A 柱の破壊モードを、せん断終局耐力(Qsu)が式(2)を満足する場合は曲げ破壊、満足しない場合はせん断破壊とする。
Q su ≧ 1.25 Q M 式(2)
ここに、Q M :柱脚に塑性ヒンジ発生以後の柱の最大せん断力
式(2)の条件より、当該柱の破壊モードを曲げ破壊とするために必要なせん断終局耐力(Q su )の下限値( min Q su )を、M0及び h0を用いて表記せよ。柱のせん断終局耐力(Q su )は軸方向力やシアスパンの変動にかかわらず一定とする。
答え
[ 解答解説 ]
・Q M
の算定
ステップAの時の柱せん断力 Q A
を算定する。
A
Mu = Mo × (bDFc − 0.4bDFc) / (bDFc − 0.4bDFc) = Mo
Q A
= (0.2Mo + AMu)/ho = (0.2Mo + Mo) /ho= 1.2Mo / ho
Q A
> Q B
につき、柱脚に塑性ヒンジが発生以後の柱の最大せん断力Q M
は下記となる。
Q M
= Q A
= 1.2Mo / ho
・ min
Q su
の算定
破壊モードを曲げ破壊とするためには式(2)を満足する必要があることから、 min
Q su
は以下となる。
min
Q su
= 1.25Q M
= 1.50 Mo/ho
?B 当該柱について、構造特性係数Dsの算出に用いる種別を告示に従って判定せよ。なお、当該柱は下記の条件によるものとし、取り付く梁の種別は考慮しなくてよい。
・上記?Aの min Q su 以上のせん断終局耐力(Q su )が得られる帯筋が配筋されている。
・柱のせい(D)に対する内のり高さ(h 0 )の比は2.8である。
・主筋の引張鉄筋比(pt)は1.0%である。
・増分解析におけるコンクリートの設計基準強度(Fc)に対する柱の平均せん断応力度(τ u )の比の最大値は0.125である。
答え
[ 解答解説 ]
これまでの回答及び、問題文中の値から、下表に従って判定する。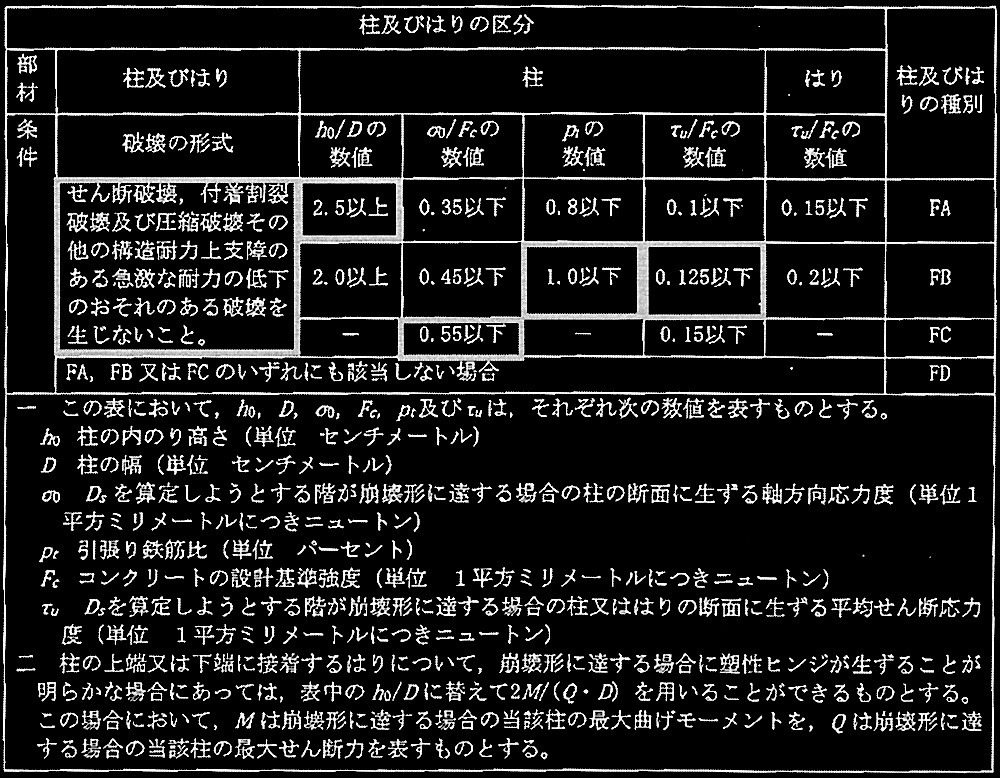
問題文の条件では、せん断破壊、圧縮破壊以外の構造耐力上支障のある急激な耐力の低下のおそれのある破壊の有無は確認できないが、そのような破壊が生じない条件においては、上記より当該柱の種別はFCと判定される。
- no image