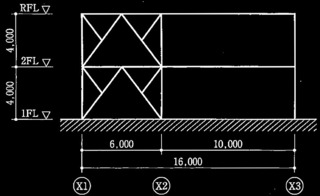
図1に示す2層の鉄骨造ラーメン構造の建築物の崩壊メカニズムに関する次の設問について解答せよ。柱及び梁の断面、材種、基準強度F及び塑性断面係数Zpは、表のとおりとする。なお、H形鋼の柱 C2は、図の面内に強軸を有するものとする。
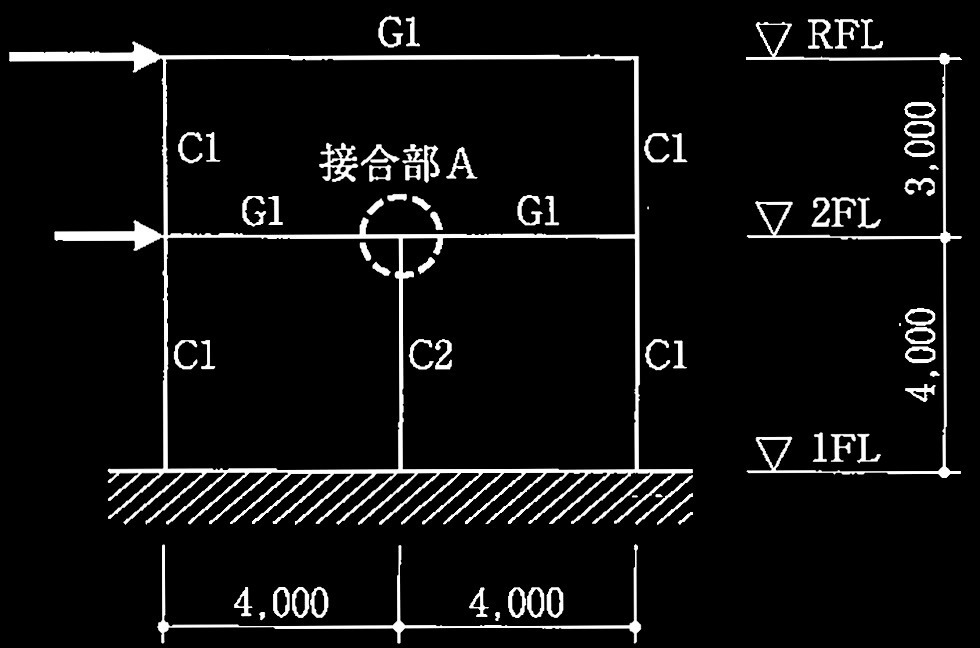
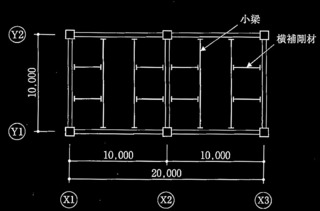
図1 骨組の解析モデル図 (単位:mm)
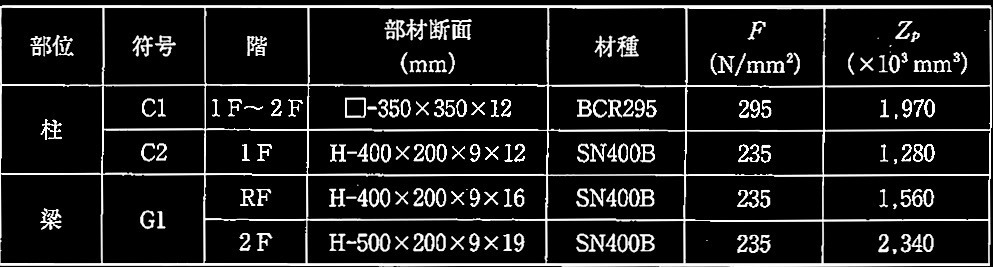
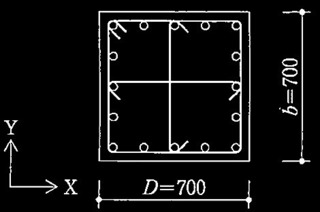
表 柱及び梁の諸元
[ No.1 ]
図1のように左方向から水平力が作用した場合の、全体崩壊形のメカニズム形成時の塑性ヒンジの発生位置を示せ。ただし、梁は保有耐力横補剛されており、柱梁接合部及び部材の中間部に塑性ヒンジは発生しないものとし、柱には柱脚部に塑性ヒンジが発生するものと仮定する。また、柱及び梁の全塑性モーメントは全断面有効と仮定して算定し、柱の全塑性モーメントの軸力による低減はないものとし、柱及び梁の長期荷重による曲げモーメントは無視できるものとする。
答え
[ 解答解説 ]
・全塑性モーメントの算定
(降伏強度は基準強度の1.1倍とする)
柱 1,2F
C1,cMp = cF × cZp
= 295 × 1.1 × 1,970 × 10 3
/10 -6
= 639 kN・m
柱 1F
C2 cMp = cF× cZp
= 235 × 1.1 × 1,280 × 10 3
/10 -6
= 331 kN・m
梁 R
G1 bMp = bF× bZp
= 235 × 1.1 × 1,560 × 10 3
/10 -6
= 403 kN・m
梁 2
G1 bMp = bF× bZp
= 235 × 1.1 × 2,340 × 10 3
/10 -6
= 605 kN・m
・ヒンジ位置の発生位置
RF 側柱 cMp( 2
C1) > bMp( R
G1)
につき、梁端部にヒンジが発生する
2F 側柱 cMp( 2
C1)+cMp( 1
C1) > bMp( 2
G1)
につき、梁端部にヒンジが発生する
2F 中柱 cMp( 2
C2) く2 × bMp( 2
G1)
につき、柱端部にヒンジが発生する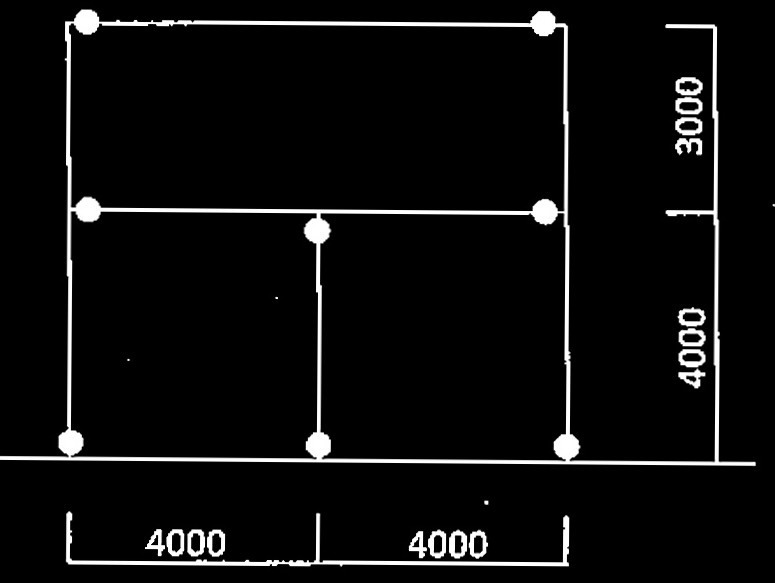
骨組のヒンジ発生位置を示す図(●がヒンジ発生位置)
[ No.2 ]
[ No.1 ]の崩壊メカニズム形成時における左側の柱C1について、2階の軸力 2F(C1-L) Nu及び 1階の軸力 1F(C1-L) Nuを求めよ。ただし、柱軸力は圧縮を正とし、左側の柱C1の2階の長期軸力は150kN、 1階の長期軸力は 300kNとする。なお、全塑性モーメント算定時の鋼材の降伏強度は基準強度の1.1倍とし、塑性ヒンジの発生位置は節点位置としてよい。
答え
[ 解答解説 ]
問題 [ No.1 ]で求めたヒンジ位置から軸力を算定する。
・2階軸力の算定
梁端部にヒンジが発生することから、崩壊メカニズム形成時の柱付加軸力は下式となる。
2F(C1-L)
N E
=2 × bMp ( R
G1)/梁スパン= 2 × 403kN・m/ 8m = 101kN
2F(C1-L)
N u
= 2F(C1-L)
N L
− 2F(C1-L)
N E
=150 kN –101 kN = 49 kN
・1階軸力の算定
側柱は梁端部、中柱は柱頭にヒンジが発生することから、崩壊メカニズム形成時の柱付加軸力は下式となる。
1F(C1-L)
N E
= ( bMp( 2
G1) + cMp( 1
C2) /2) / 梁スパン=(605 kN・m + 331 kN・m/ 2) /4m
= 193 kN
1F(C1-L)
N u
= 1F(C1-L)
N L
− ( 2F(C1-L)
N E
+ 1F(C1-L)
N E
)=300 kN − (193 kN + 101 kN)
= 6 kN
梁の曲げモーメント・せん断
[ No.3 ]
[ No.1 ]の崩壊メカニズム形成時の2階の保有水平耐力 2F Q u 及び1階の保有水平耐力 1F Q u を求めよ。なお、 2階側柱の曲げモーメントの反曲点高さは、階高の0.3倍とする。
答え
[ 解答解説 ]
問題 [ No.1 ]で求めたヒンジ位置から保有水平耐力を算定する。
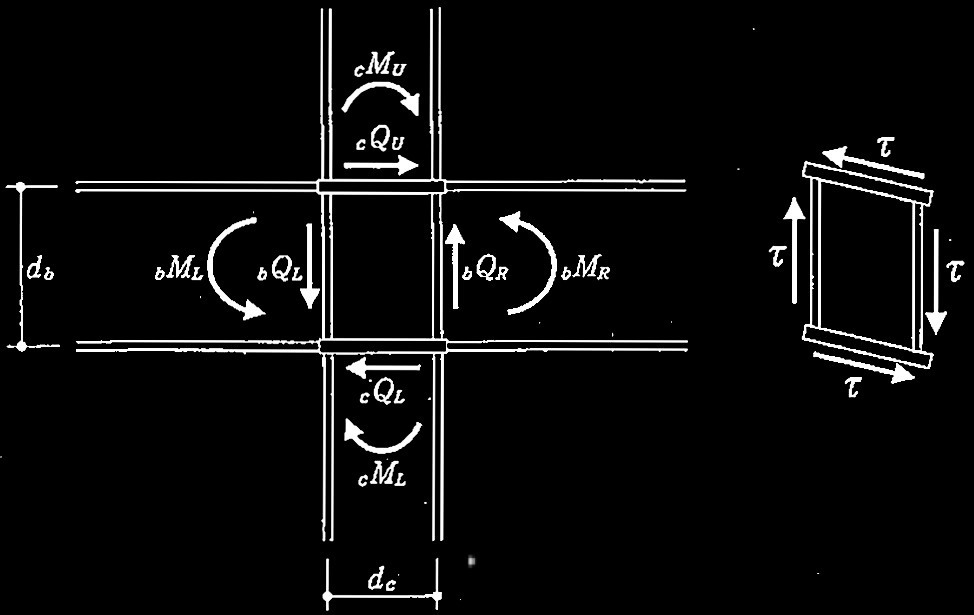
・崩壊メカニズム時の曲げ応力及びせん断力分布は下図となる。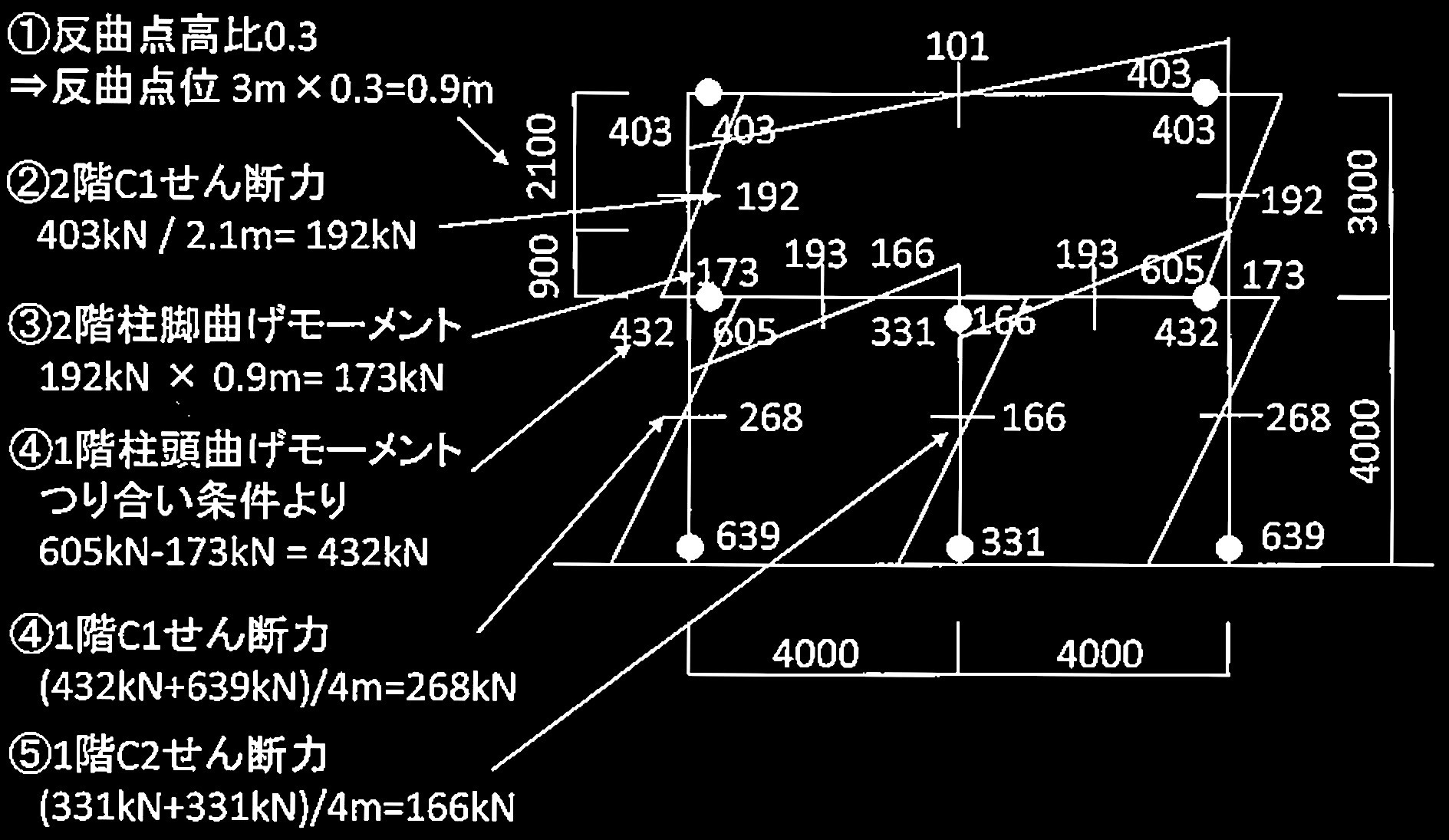
・保有水平耐力は下式となる。
2F
Q u
= 192 kN + 192 kN = 384 kN
1F
Q u
= 268 kN + 166 kN + 268 kN = 702 kN
[ No.4 ]
[ No.1 ]の崩壊メカニズム形成時の中柱C2の接合部パネル(図1の接合部A)のせん断応力度 p τを式(1)により、接合部パネルの終局せん断強度 p τ u を式(2)により求め、それらの値の比較により、接合部パネルが塑性化するか否かを判断せよ。なお、接合部パネルの板厚及び基準強度は柱ウェブと同じとし、接合部パネルの終局せん断強度に与える柱軸力の影響は無視できるものとする。
次に、接合部パネルを塑性化させないための構造設計上の対策を2点挙げよ。なお、柱及び梁の断面寸法(部材せい、部材幅)の変更はできないものとする。

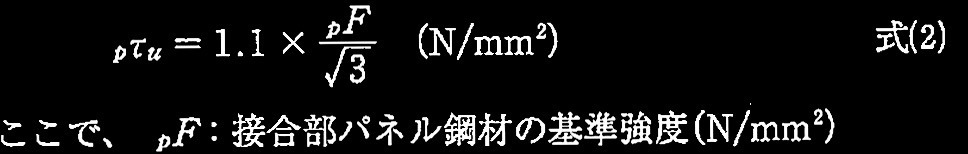
(引用:日本建築学会「鋼構造接合部設計指針」一部編集)
答え
[ 解答解説 ]
問題文中の「pMp:接合部パネルの全塑性モーメント」は「鋼構造接合部設計指針(日本建築学会 2012)」の「pM:接合部パネルモーメント」として計算式を用いる。また図中の接合部パネルの図は、指針の図と異なり、せん断力が卓越した場合を示している。
d c
= 0.4m – 0.012m = 0.388m
d b
= 0.5m – 0.019m = 0.481m
t p
= 0.009m
[ No.3 ] 解答の応力図より
p
M p
= 331 kN・m − (193 kN + 193kN) × 0.388 m/2 = 256 kN・m
V e
= 0.388m × 0.481m × 0.009m = 0.00168m 3
p
τ = 256 kN・m/ 0.00168m 3
×10 -3
= 152 N/mm 2
p
τ u
= 1.1 × 235 kN/mm 2
/ √ 3 =149 N/mm 2
< p
τ = 152 N/mm 2
以上より、接合部パネルは塑性化する
接合部パネルを塑性化させない構造設計上の対策(例)
・柱梁仕口部を組立材とし、接合部パネル厚を確保する。
・接合部パネルにカバープレートやスチフナプレートを溶接することにより補強する。
・接合部パネルの鋼材強度を大きくする。