問題1
図1に示す筋かい付き鉄骨架構及び座屈補剛モデルについて、以下の[ No.1 ]〜[ No.3 ]の設問に解答せよ。なお、本架構の接合部は保有耐力接合されており、柱及び梁の耐力は十分に大きく、柱及び梁の座屈は生じないものとする。
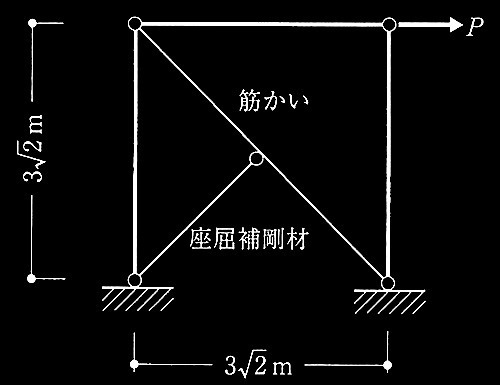
図1 筋かい付き鉄骨架構
[ No.1 ]
図1に示す鉄骨架構の筋かい材はH形鋼で、断面積 A = 6,000 mm 2 、断面二次半径 i x = 100mm、i y = 40mmであり、構面内が弱軸曲げになるよう、フランジ面と紙面が平行に配置されている。鋼材はSN400材(F値235 N/mm 2 )であり、圧縮材の座屈の 長期許容応力度fcは式(1)で得られるものとする。座屈補剛材は筋かいの中央に取り付き十分な強度と剛性を有しているものとして、筋かいの 短期許容圧縮耐力Ncを求めよ。

答え
[ 解答解説 ]
(筋かいの強軸側)
筋かい強軸に対する座屈補剛はないので、筋かいの圧縮座屈長さ?は、
?= 3√2 × √2 = 6m
圧縮筋かいの両端部は面内並びに面外方向にも材軸直行方向の移動が拘束されたピン固定とすると、筋かい強軸側の細長比λは
λ = ? /i x
= 6,000mm/100mm = 60
(筋かいの弱軸側)
筋かい弱軸に対して、十分な剛性と耐力を有する補剛材により、座屈補剛されていることから、筋かいの圧縮座屈長さ?は、
? = 3√2 / √2 = 3m
座屈補剛区間内の圧縮筋かいの端部は面内並びに面外方向にも材軸直行方向の移動が拘束されたピン固定とすると、筋かい弱軸側の細長比λは
λ = ?/i y
= 3,000mm/40mm=75
以上より細長比は弱軸側の方が大きいため、弱軸側の座屈性能で決まる。
限界細長比Λは問題文の式よりΛ = 1,500/ √ (235N/mm 2
/1.5) = 120
となる。
以上より
λ = 75 ≦ Λ =120
であるため、fcは式(1)の上段に示された式を用いて
fc = {1 - (2/5)(75/120) 2
/ (3/2+ (2/3)(75/120) 2
)} × 235N/mm 2
= 112.6 →113 N/mm 2
Nc = 1.5 × A × fc
= 1.5 × 6000mm 2
× 113 N/mm 2
= 1,017,000N = 1,017kN →1,020kN
[ No.2 ]
日本建築学会「鋼構造許容応力度設計規準(2019年版)」では、必要補剛力は圧縮力の2 %、補剛材の剛性は実験と解析に基づき、4N/?k以上としている。
これを本問題の記号で示すと以下のようになる。
Fr = 0.02Nc (kN)
K ≧ 4Nc/? (kN/m)
この式を用いて図1に示す座屈補剛材に要求される必要補剛力Fr 及び必要補剛材剛性 K を求めよ。ここで、?とは補剛間長さである。
答え
[ 解答解説 ]
必要補剛力Fr及び必要補剛材剛性Kは問題文中の式より、
Fr = 0.02 Nc = 0.02 × 1,020 = 20.4 kN
K = 4Nc/? = 4 x 1,020 / 3 = 1,360 kN/m
[ No.3 ]
図2は、元たわみがある場合の座屈補剛材に要求される剛性と補剛力を求めるための簡単なモデルである。以下の問いに答えよ。
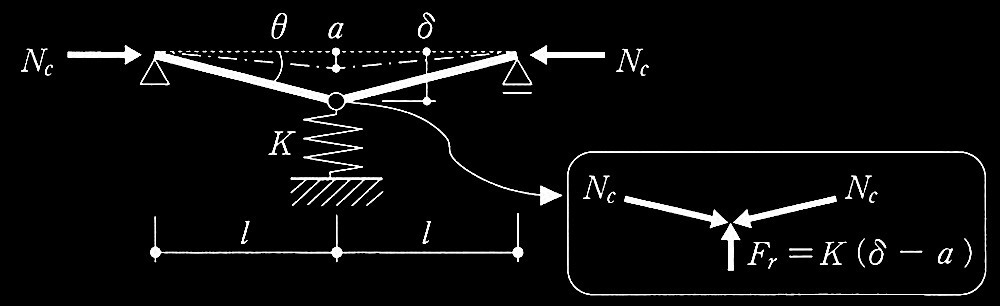
図2 元たわみがある場合の座屈補剛モデル
?@ 元たわみがある場合の座屈補剛モデルについて、必要補剛力及び必要補剛材剛性の関係を誘導した以下の文中の空欄[ ア ]〜[ ウ ]に入る記号、数式または数値を解答欄に記入せよ。
図2に示すように、座屈する部材と補剛材を、部材中央で剛性Kのばねで補剛され、両端と中央でピン接合された剛棒でモデル化している。元たわみをaとすると、中央点の鉛直方向のカのつり合い式は、式(2)となる。
2Ncθ = Fr = K( δ − a ) = K( [ ア ]•θ − a ) 式(2)
式(2)よりθを消去して、必要補剛力比 Fr/ Nc と必要補剛材剛性比K?/(2Nc)の関係を求めると式(3)となる。
Fr / Nc = 4K? / (2Nc)/{ K?/(2Nc) − [ イ ] } ・ [ ウ ] 式(3)
答え
[ 解答解説 ]
θが微小の場合、δ ≒ ?・θ ・・・ ア:?
式(2)よりθについて解くと、
θ = Ka/(K? − 2Nc) ・・・ 式(2-a)
とする。
一方、同じく式(2)の左側から、
Fr/Nc = 2θ ・・・ 式(2-b)
とする。
式(2-a)を式(2-b)に代入し、分母と分子を2Ncで除すと、
Fr/Nc = 2Ka / (K?− 2Nc)
=2Ka / (2Nc)/(K?/(2Nc)−1)
右辺について、式(3)の分子である4K?/(2Nc)を出して整理すると、
Fr/Nc = {4K?/(2Nc)/(K?/(2Nc)−1)} ・a/2?
以上より、 イ:1、 ウ:a/2?
?A 式(3)より、元たわみaが ?/250の場合(aが全長の1/500の場合)の必要補剛材剛性比 Fr/ Ncと必要補剛力比 K?/(2 Nc)との 関係曲線を答案用紙に描け。また、[ No.2 ]で示した必要補剛力、必要補剛材剛性に相当する点をその 図中に黒丸(●)で示せ。
答え
[ 解答解説 ]
式(3)において、K?/2Nc=X、a=?/250とすると、
Fr / Nc = 4X/(X −1) × (?/250)/2? = (4/500)X/(X-1)
Xを横軸、Fr/Ncを縦軸として、グラフを下記に示す。
問題No.2の必要補剛力、必要補剛材剛性に関する諸数値は以下の通りである。
X = K?/2Nc = 2
Fr/Nc = 0.02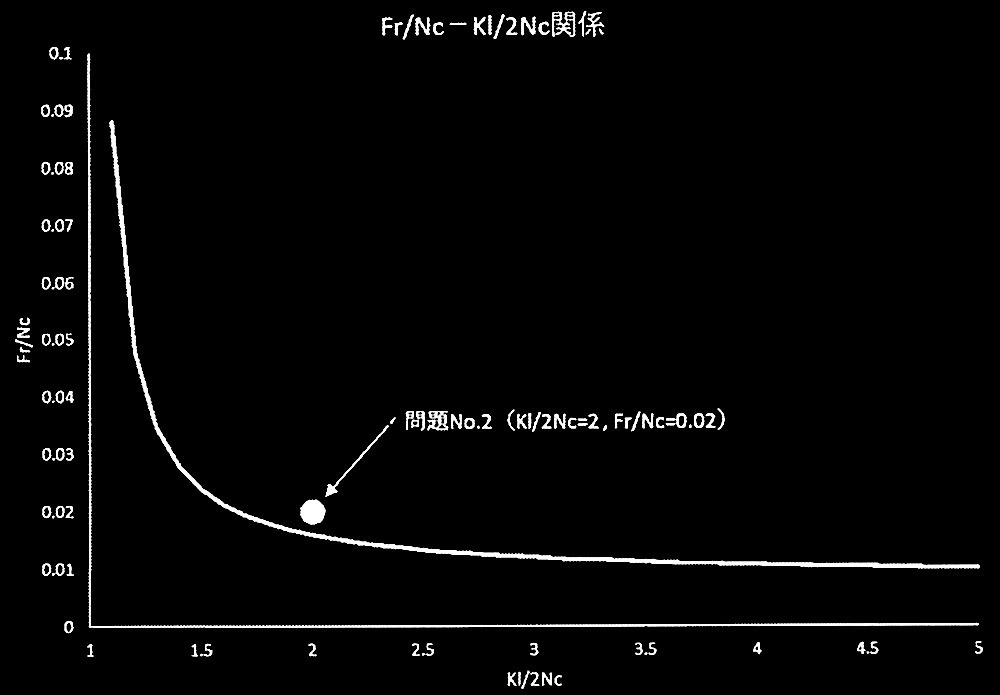
?B 日本建築学会「鋼構造限界状態設計指針•同解説」では、必要補剛力 Fr = 0.03 Nc 及び必要補剛剛性 K=4Nc/?が与えられている。この場合、 どの程度の元たわみまで耐えうるかを、補剛区間長さ?に対する比で解答せよ。
答え
[ 解答解説 ]
式(3)において、左辺=Fr/Ne= 0.03
またK = 4Nc/?より、K?/2Nc = 2
以上を式(3)に代入すると、
0.03 = 4 × 2 / (2 − 1) × (a/2?)
a = (3/400) •?
以上より、 耐えうる元たわみaの補剛区間長さ?に対する比は3/400である。