問題2
鉄筋コンクリート造連層耐力壁に関する次の[ No.1 ]及び[ No.2 ]の設問に解答せよ。
[ No.1 ]
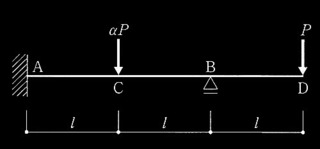
図1に示すスパン?w、各階高さHの3層の連層耐力壁の各階に水平力が作用している。水平力の大きさは、2階床で P、3階床で2P及び屋上階で3Pである。
耐力壁の水平断面は図2に示すような I形断面で、柱中心間距離は?wである。各階の引張側柱と圧縮側柱の断面と配筋は同一で、1階耐力壁には圧縮軸力Nが作用している。基礎と基礎梁は剛強とし、諸性能の算定を簡略に行えるよう基礎梁の効果は無視して、1階柱脚部をピン支持(図1の△印)とする。
この架構の耐力を求めるための以下の記述の空欄[ ?@ ]〜[ ?E ]に入る数式を、また、[ ?F ]〜[ ?H ]に入る数値を解答欄に記入せよ。
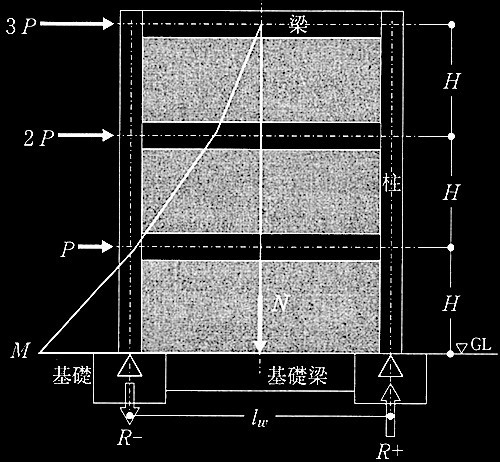
図1 水平力を受ける連層耐力壁の曲げモーメント図


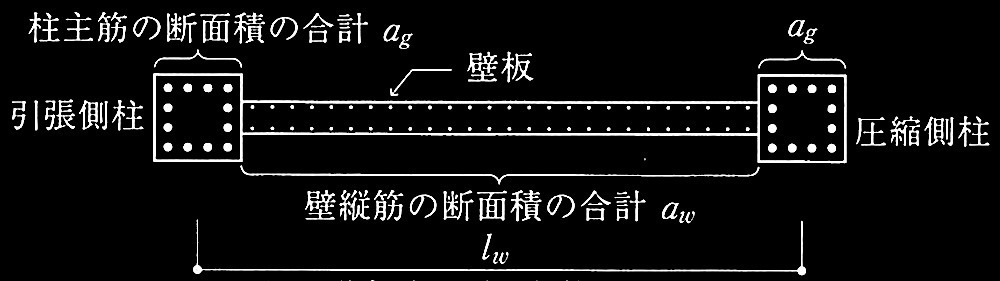
図2 耐力壁の断面と柱中心間距離
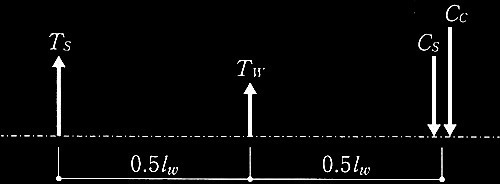
図3 曲げ終局強度Mu時の各断面力の大きさと向き
連層耐力壁の曲げモーメント分布が図1に示すようになり、1階壁脚部で曲げ終局強度Muとなるときを考え、このMuの算定式を導く。曲げ終局強度Mu時の断面力は図3に示すように、引張側柱の全主筋が引張降伏したときの引張力Ts、耐力壁の全縦筋が引張降伏したときの引張力Tw、圧縮側柱の全主筋が圧縮降伏したときの圧縮力Cs、及び圧縮側柱のコンクリートの圧縮合力Ccからなるものとする。 Ts、 Cs、及びCcは柱中心に作用し、 Twは壁板中心に作用するものとする。
断面に下向きに作用する軸力Nは、 Ts、 Tw、 Cs、及びCcを用いて、N =[ ?@ ]と表される。
また、両柱の断面寸法及び配筋は等しいためCs =[ ?A ]となる。よって、軸力Nは、コンクリートの圧縮合力Cc及びTwだけを用いて、N=[ ?B ]と表せる。これらの関係から、曲げ終局時強度Muは、図3に示す断面力による壁の断面中心に対するモーメントとして計算でき、 Ts、 Tw、N、及び ?wだけを用いて、Mu = [ ?C ]と表せる。
一方、図1に示すような水平力が作用しているときに、連層耐力壁の脚部に発生するモーメントMの大きさは、水平力の基準値P及び各階の階高 Hを用いて、M =[ ?D ]と表せる。また、そのときに1階に作用しているせん断力Q B はPを用いて、 Q B =[ ?E ]と表せる。
ここで、?w = 6,000 mm、H =3m、N = 2,100 kN、a g = 4,900 mm 2 、a w = 4,200 mm 2 、σ y = σ wy = 350 N/mm 2 とすると、曲げ終局強度 Muは[ ?F ]kN•m、Pの大きさは[ ?G ]kN、1階に作用しているせん断力Q B は[ ?H ]kNとなる。
答え
[ 解答解説 ]
Ts、Tw、Cs、Ccは図の矢印の方向を正とする 曲げは壁脚部において時計回りを正とする。
計算は有効数字3桁で行い、結果も有交数字3桁で示す。処理は、四捨五入とする。
?@Ts、Tw、Cs、Ccの合力は軸力Nとなるため、
N = −Ts −Tw + Cs + Cc
となる。
?A配筋量が同じであり、全主筋が圧縮降伏したときの圧縮力Csと引張縮降伏したときの引張力圧縮力Tsは大きさが同じため、
Cs = Ts
となる。
?B ?Aより−Ts + Cs = 0となるため、?@の式よりTsとCsが消え、
N = −Tw + Cc
となる。
?C曲げ終局強度Muは、壁脚部中心位置でTs、Tw、Cs、Ccにより算定すると、
Mu = Ts × 0.5 ?w + Tw × 0.0 ?w + Cs × 0.5 ?w + Cc × 0.5 ?w
となるが、?AよりCs = Ts、
?BよりN = −Tw + Ccのため、Cc = Tw + Nにより、
Mu = Ts × ?w + Tw × 0.5 ?w + N × 0.5 ?w
となる。
?D連層耐震壁の脚部に発生するモーメントMは、
M = 3P × 3 × H + 2P × 2 × H + P × Hより、
M = 14 × P × H
となる。
?E 1階に作用しているせん断力 Q E
は、
Q E
= 3P + 2P + Pより、
Q E
= 6 × P
となる。
?F曲げ強度Muは、
耐力壁の柱中心間距離 ?w = 6,000mm = 6.0m
各階の高さH = 3m
1階の耐震壁に作用する圧縮軸力 N = 2,100kN
柱1本の主筋の断面積の合計 a g
= 4,900 mm 2
壁縦筋の断面積の合計 a w
= 4,200mm 2
柱主筋の降伏強度σ y
= 壁縦筋の降伏強度 σ wy
= 350N/mm 2
より、
Ts = a g
× σ y
= 4,900 mm 2
× 350N/mm 2
/1,000
= 1,715kN→1,720kN
Tw = a w
× σ wy
= 4,200mm 2
× 350N/mm 2
/1,000
= 1,470kN
を用いて、?Cの式より、
Mu = 1,720kN × 6.0m+ 1,470kN × 0.5 × 6.0m +2,100kN × 0.5 × 6.0m
=21,030 kN•m→ 21,000 kN•m
となる。
?G Pの大きさは?Dの式より、
P = M/(14 × H)となるため、
P = 21,000kN•m/(14 × 3.0m)
= 500 kN
となる。
?H 1階に作用しているせん断力Q E
は、?Eの式QE = 6 ×Pより
QE = 6 × 500kN
= 3,000 kN
となる。
[ No.2 ]
[ No.1 ] のような応力状態で、1階の耐力壁がせん断破壊を生じないようにするためには、?Hで求めた曲げ終局強度時のせん断力に対して、せん断終局強度は1.25倍以上の余裕度を有することが求められている。一方、梁部材の両端でヒンジが形成される場合は、両端ヒンジ状態でのせん断力に対して、1.1倍以上の余裕度を有することが求められている。連層耐力壁が両端ヒンジ状態の梁よりも、大きなせん断余裕度が求められている 主たる理由を1つ述べよ。
答え
[ 解答解説 ]
く主たる理由>
保証設計において、梁の両端ヒンジ状態のせん断破壊に対する余裕度は材料強度のばらつきを考慮したものであるが、連層耐震壁では曲げ終局状態時のせん断力に対して、材料強度のばらつきと、外力分布のばらつきにより連層耐震壁に生じる曲げモーメントとせん断力の関係が変化する分も加えた余裕度を用いてせん断破壊を生じないようにする必要があるため。