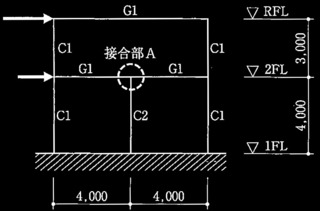
図1に示す2層2スパンの鉄骨造骨組の設計に関する次の設問について解答せよ。耐震計算ルートは3とし、柱、大梁及び筋かいの材料特性及び断面性能等の諸元は表1〜表3のとおりである。なお、筋かいは、構面内曲げが弱軸回りとなるように配置され、部材中央部を筋かいと同断面の部材により座屈補剛されているものとする。
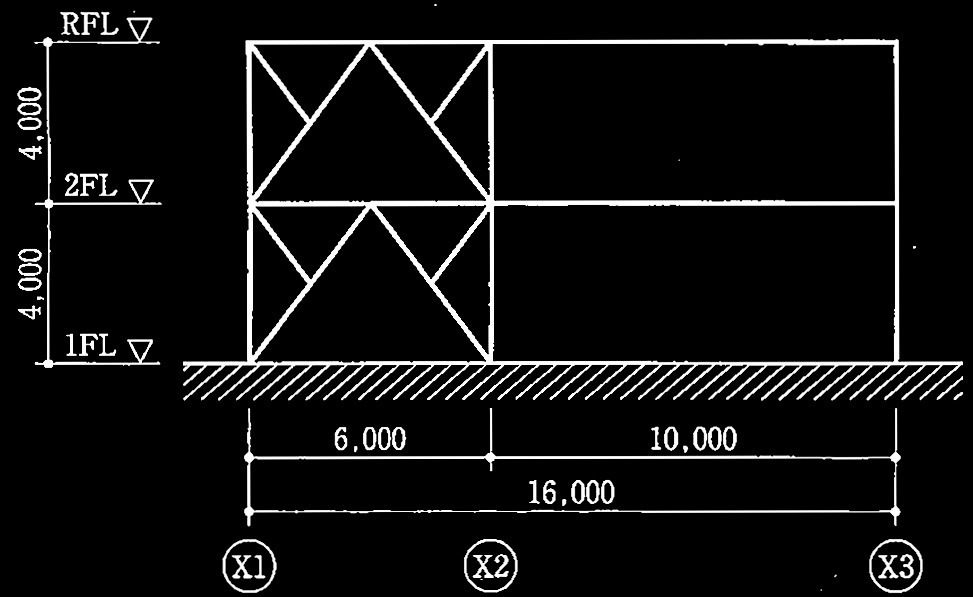
図1 骨組のモデル図(単位:mm)
表1 柱の諸元

表2 大梁の諸元

表3 筋かいの諸元


[ No.1 ]
地震時に高レベル応力を繰り返し受ける柱梁接合部の仕口部の溶接部には、瞬間的な亀裂の伝搬を伴う脆性破壊を避けるため、強度の他に靱性も要求される。大梁端部での脆性破壊を防止し、安定した塑性変形能力を確保するため、柱梁接合部の仕口部の溶接について、「構造設計」及び「鉄骨製作」それぞれの段階で特に留意すべき点を簡潔に述べよ。
答え
[ 解答解説 ]
「構造設計」で留意すべき点(例)
・切欠き状の欠陥の回避(応カ・ひずみ集中源の除去)
ノンスカラップ工法の採用など
・高い靱性材料の採用
・梁端部拡幅工法などにより、塑性ヒンジが溶接位置で発生しないようにする
「鉄骨製作」で留意すべき点(例)
・熱影響部などの品質を確保するための入熱・パス間温度の管理
・ショートビードの回避や予熱の併用
[ No.2 ]
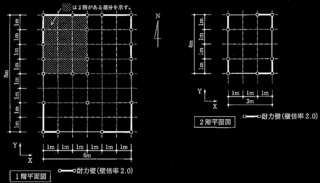
図1に示す鉄骨造骨組が下記(a)~(c)の条件にある場合について、次の?@及び?Aの設問に解答せよ。
(a) 各部材の接合部は保有水平耐力接合を満足している。
(b) 柱及び大梁の幅厚比は、全て種別FAを満足し、大梁は全て保有耐力横補剛されている。
(c) 柱脚部は露出柱脚であるが、保有水平耐力接合を満足している。Ds値の割増しは必要ない。
?@ 1階の筋かいについて、部材としての種別を昭和55年建設省告示第1792号(以下、「告示」という。)に従って判定し、種別判定の根拠を簡潔に記述せよ。
答え
[ 解答解説 ]
1階の筋交い長さ L = √(4,000 2
+ 3,000 2
) = 5,000 mm
筋交いの細長比
強軸 座屈長さ 5,000 mm
λ x
= L / i x
= 5,000 mm / 86.2 mm = 58.0
弱軸 座屈長さ 5,000 mm/ 2 = 2,500 mm
λ y
= L / i y
= 2,500 mm/ 50.2 mm = 49.8
部材の細長比 λ = max(λ x
, λ y
) = 58.0
?昭和55年建設省告示第1792号・第3 (最終改正平成19年5月18日国土交通省告示第596号)より
(495 / √ F = 32.3) < ( λ= 58.0) < (890/√ F =58.1)であるから、
部材種別BB
?A 1階の部材群としての種別を告示に従って判定し、各階の構造特性係数D s 値を求めよ。また、部材群としての種別判定の根拠及びD s 値の算定根拠も簡潔に記述せよ。なお、B u は 0.4とする。
答え
[ 解答解説 ]
柱及びはりの部材群としての種別 A
柱及びはりの全部材がFA材であることから、γ A
=1.0 ≧ 0. 5
∴ 柱及びはりの部材群としての種別はA
筋交いの部材群としての種別 B
筋かいの全部材がBB材
∴ 筋かいの部材群としての種別はB
柱及びはりの部材群としての種別A、筋かいの部材群としての種別B、0.3く(β u
= 0.4) ≦ 0.7
? 昭和55年建設省告示第1792号・第3 (最終改正平成19年5月18日国土交通省告示第596号)より
D s
値 0.3
[ No.3 ]
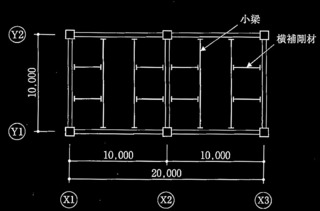
図2のように2階のX2~X3通りの大梁は、中央部分に吹抜けを設けるプランであるため全長にわたり均等間隔で横補剛をすることができない。その対応策として、両梁端部に1箇所ずつ横補剛する場合について、次の?@及び?Aの設問に解答せよ。
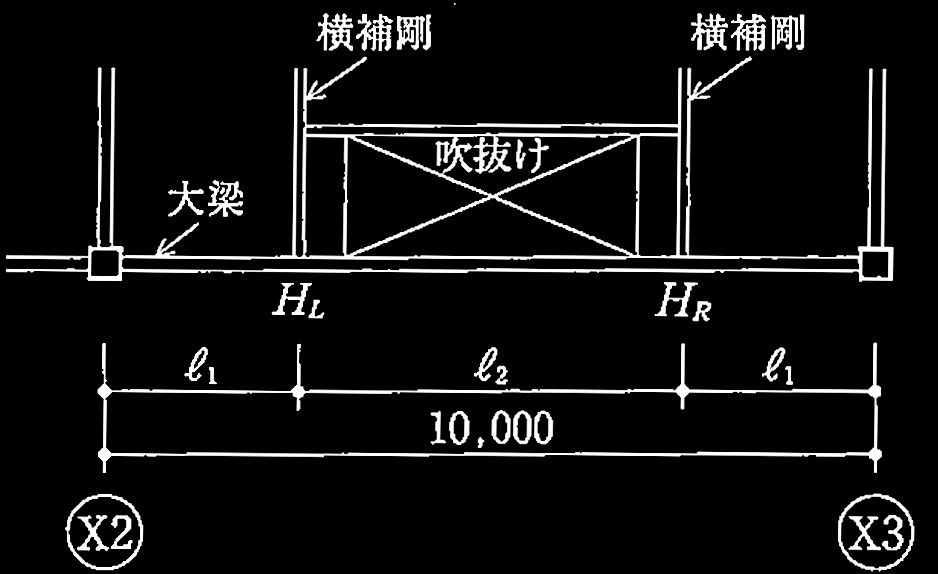
図2 2階X2〜X3通りの大梁周囲の平面図(単位:mm)
?@ X2通りから横補剛材の位置までの最大距離 ?1を下式により求めよ。なお、下式は 400ニュートン級炭素鋼の梁の横座屈を防止するために、梁の端部に近い部分に横補剛を設けるときの条件式である。

(出典:2015年度版建築物の構造関係技術基準解説書)
答え
[ 解答解説 ]
i y
= 47.4 mm
A f
= 200 × 22 = 4400 mm 2
h = 500 mm
? b
≦ 250 × A f
/h = 2200 mm
かつ
? b
≦ 65 × i y
= 3081 mm
柱フェイス位置にヒンジができるとした場合、
? 1
=2200 + 350/2 = 2375 mm
?A 左右の横補剛材の位置を?@で求めた ? 1 で決定し、その位置をそれぞれH L 、H R とするとき、H L 〜H R 間には横補剛が不要であることを計算により示せ。ただし、横補剛検討用の曲げモーメント分布には、安全率 α= 1.2を乗じたものを用いるものとし、M p の算定に用いる材料強度は、基準強度 F値の1.1倍とする。また、長期荷重は無視するものとする。なお、H形断面部材の長期許容曲げ応力度は次により求めるものとする。

(平成13年国土交通省告示第1024号第1第三号ハ表1(1)(抄))
答え
[ 解答解説 ]
両端降伏時の梁端部の曲げモーメント
αM p
= 1.2 × Z p
× 1.1F
=1.2 × (2,600 × 10 3
)mm 3
× 1.1 × 235N/mm 2
× 10 -6
= 8.07 × 10 8
N・mm = 807kN・m
柱フェイス位置で両端がαM p
となるときの梁端部から? 1
の位置での曲げモーメント
梁内法スパン 10,000mm −350mm = 9,650 mm
M ?1
= 807 kN・m × (9,650 mm − 2,200 mm × 2) / 9,650 mm= 439 kN・m
H L
〜H R
間の端部曲げモーメントが上述のM 1
= M 2
となるときのH L
〜H R
間の短期許容曲げモーメントM s
M 1
= M 2
= 439 kN・m
曲げモーメント分布が複曲率なのでM 2
/M 1
= 1.0
∴ C = 1.75 + 1.05 × 1.0 + 0.3 × 1.0 2
= 3.10
→ C= 2.3
Λ = 1500/√ (235/1.5) = 120
? b
= 10,000 mm – 2,375mm × 2
= 5,250mm (H L
〜H R
間の長さ)
i b
= 54.0mm
A f
= 200mm × 22 mm = 4,400 mm 2
h= 500 mm
f b1
= 235 x (2/3 – 4/15 × (5250 / 54.0) 2
/ (2.3 × 120 2
)) = 139 N/mm 2
f b2
=89000/(5250 x 500 / 4400) = 149 N/mm 2
f b
= max(f b1
,f b2
) = f b2
=149 N/mm 2
よって短期許容曲げモーメントM s
は、
M s
= Z x
× 1.5 × f b
= (2,330 × 10 3
) mm 3
× 1.5 × 149 N/mm 2
= 4.89 × 10 8
N・mm = 521 kN・m
M ?1
(439kN・m) < M s
(521 kN・m)となり、梁の両端がαM p
に達するときの梁端部から? 1
の位置での曲げモーメントM ?1
は、短期許容曲げモーメントM s
より小さい。
H L
~H R
間には横補剛は不要である。