問題2
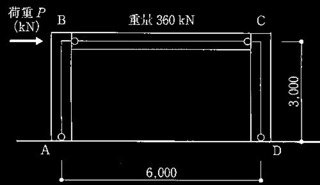
図1に示す偏心K形筋かい付き鉄骨架構の柱頭部に水平力が作用した場合について、次の[ No.1 ]〜[ No.4 ]の設問について解答せよ。各部材の断面形状、材料特性、断面性能の諸元を表1に示す。部材の終局耐力の計算にはF値を用いることとし、1.1倍しない。なお、節点B、節点Eは、構面外拘束されているものとする。
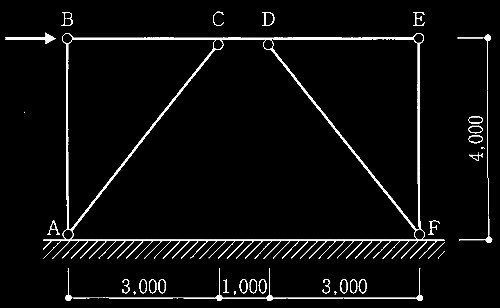
図1 偏心K形筋かい付き門形骨組(単位:mm)
表1 各部材の断面形状•材料特性•断面性能

計算は有効数字3桁で行い、結果も有効数字3桁で示す。処理は、四捨五入とする。
[ No.1 ]
梁の全塑性モーメントM p を求めよ。なお、軸力の影響は考慮しなくてよい。
答え
[ 解答解説 ]
M p
= Z p
(塑性断面係数)× 材料強度(= F値)
=2.1 × 10 6
× 235
= 4.94 × 10 8
(Nmm)
= 494 (kNm)
[ No.2 ]
筋かいACと筋かいDFは座屈せず圧縮・引張が同一軸力で降伏する座屈拘束ブレースとし、軸降伏耐力は 1,200 kNである。梁にせん断降伏や横座屈が生じないものと仮定した場合のメカニズム時のモーメント図及びせん断力図を描け。また、その値を記入し、モーメントは引張側に描くこと。
答え
[ 解答解説 ]
水平力を受ける架構の曲げモーメントは下図のようになる。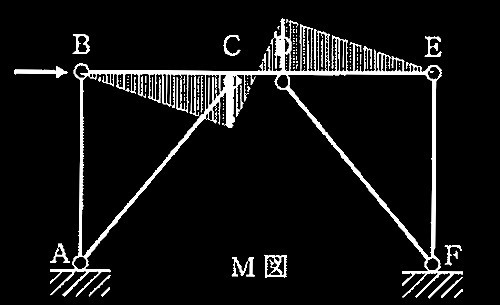
この際、筋かいが軸降伏せずC点、D点において塑性ヒンジが形成されるメカニズムを仮定すると
C点、D点における M = M p
=494(kNm)
BC間ならびにDE間のせん断力は
(M 右
– M 左
)/L
= (494 – 0.0) /3.0 (m)
= { 0.0 – ( –494)} /3.0 (m)
=165(kN)
CD間のせん断力は
(M 右
– M 左
)/L
= {( –494) – 494} /1.0(m)
= –988 (kN)
となる。
この際、C点ならびにD点でのせん断力の変化より、AC筋かい軸力の鉛直成分は、
C点{165 – ( –988)} = 1150 (kN)、
D点{( –988) – 165) = –1150 (kN)であり
筋かいの軸力Nは、
N =1150 (kN) /4.0 (m) × √(3.0 2
+ 4.0 2
)
= 1438 (kN)
となるため、筋かいの軸降伏耐力1200 (kN)を超えている。
以上より、メカニズムはAC筋かい、DF筋かいの軸降伏で生じていることが確認された。
上記の計算結果より、AC筋かいおよびDF筋かいの軸降伏によるメカニズム時の応力は
C点、D点における曲げモーメント、494 × (1200/1438)= 412 (kNm)
BC間ならびにDE間のせん断力、165 × (1200/1438) = 138 (kN)
CD間のせん断力、-988 × (1200/1438) = −824 (kN)となる。
なお、柱AB、EF、ならびに筋かいAC、DFは両端ピンで中間荷重が無いため、曲げモーメントならびにせん断力は生じていない。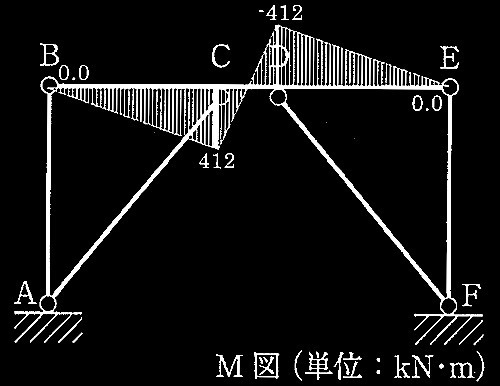
M図(単位:kN•m)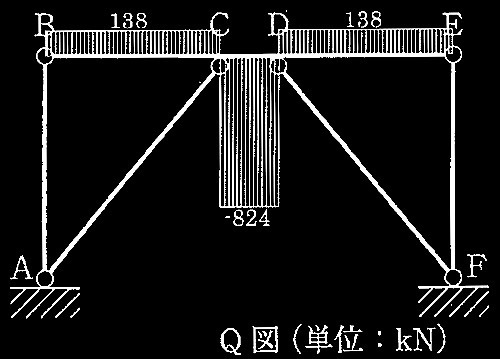
Q図(単位:kN)
[ No.3 ]
梁CDのウェブの降伏せん断力Q y を求めよ。また、梁CDは曲げ降伏するかせん断降伏するかを判定せよ。
答え
[ 解答解説 ]
終局せん断耐力を算定する際の材料強度は、
F/ √3 = 235/√3 =136 (N/mm 2
)
ウェブ断面積
A w
= (500 − 2 ×16) × 10 =4680 (mm 2
)
Q y
=136 × Aw =136 × 4680 = 636000 (N)
= 636 (kN)
[No.2]より、C点、D点において塑性ヒンジが形成されると仮定した場合の、CD間のせん断力は 988 (kN)であり、
上記 Q y
= 636 (kN)より大きい。
よって、 梁CDはせん断降伏する。
[ No.4 ]
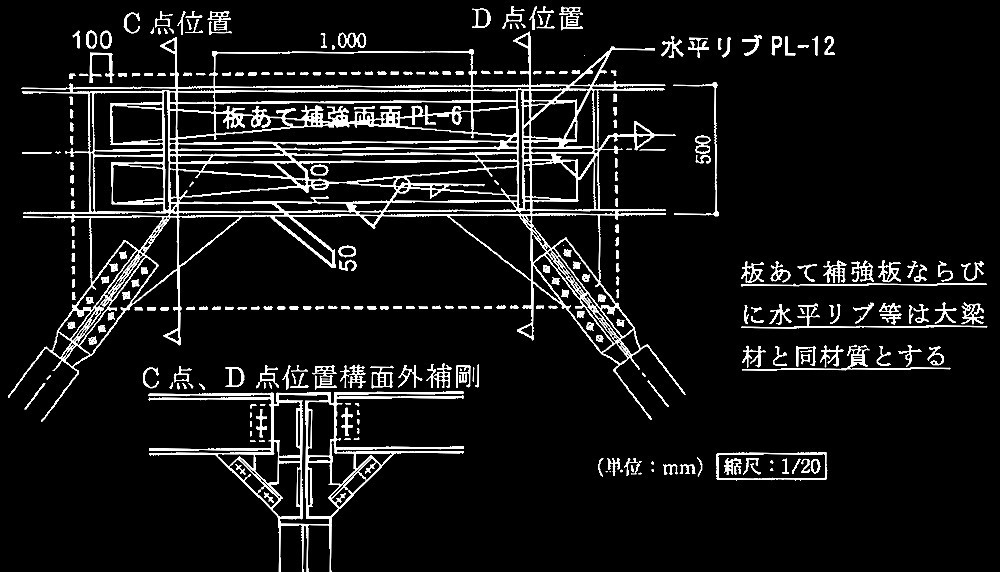
以上の解答を踏まえて、ブレースと梁の接合部が答案用紙の架構図のような場合、座屈拘束ブレースが安定してエネルギー吸収を行うために、 構面外の安定性に対する補剛とせん断耐力に対する補強を行った梁CDの接合部の 納まりをスケッチせよ。ただし、補剛・補強範囲は破線枠内とする。
答え
[ 解答解説 ]
[ No.3 ]より、ウェブ降伏せん断耐力は Q y
= 636 (kN)であり、
[ No.2 ]の、ブレース軸降伏によるメカニズムにおけるせん断力823 (kN)より小さい。
よって、CD間のウェブ降伏せん断耐力を大きくするための補強が必要である。
また、梁ウェブの幅厚比は(500 −16 × 2) /10=46.8となっており、
幅厚比(43√ (235/F) = 43)を満足していないため、中断に水平リブを設ける。
補強方法として板あて補強を採用した際の必要補強断面積および補強板の板厚は以下となる。
必要補強断面積={ (823 – 636) × 1000/136} = 1375 (mm 2
) → 1380 (mm 2
)
1枚の補強板のせいを
(500mm – 50mm × 2 – 100mm) /2 =150 (mm)
とすると、
補強板の必要板厚は、
1380mm 2
/150mm/ 4枚=2.30 (mm)
となる。
必要補強量は上記のように少ないが、十分に安全とするため、ウェブ両側に t=6 (mm) の板を溶接により接合して補強する。
また、梁下フランジにブレースが接合する位置の構面外への変形を防止するためC点、D点位置に対して補剛を行う。