PR
Keyword Search
Comments
 New!
Gママさん
New!
Gママさんイチョウの大木、サ…
 New!
隠居人はせじぃさん
New!
隠居人はせじぃさん新磯地区の寺社史蹟… New! オジン0523さん
2024年はムベが不作
 noahnoahnoahさん
noahnoahnoahさんエコハウスにようこそ ecologicianさん
Calendar
しています。
4月から始まった「3か月でマスターする」シリーズ。 世界史に続く第2弾「数学」 が
6月26日から始まったのです。
「学生時代、数学の授業やテストに苦しみ、良い思い出がないという人も多いのでは。
でも大丈夫です!」と。
全12回からなるこのシリーズ、題材は基本的に中学校の数学の教科書から選定していると。

MCはNHK・塚原愛アナウンサー
秋山仁さん(東京理科大学栄誉教授)、横山明日希さん(数学教育者)、ヨビノリたくみさん
(教育系YouTuber)3人の数学教育のプロ が、それぞれのアプローチで数学の楽しさや奥深さを
じっくりレクチャー。数学の歴史的背景や生活との関わりなど、幅広い話題を提供します。
目指すは「数学との仲直り」。あなたも一緒に大人の学び直しをしませんか!? 」と。

そして、この日は「 水平線はどれくらい先? 」と。

この日の 教材部分 。
『海岸に立って』!!何もしないでのんびり海を眺めるのはリフレッシュの一つでは。
見渡す限りの広い海の先に水平線が見える場所があります。
水平線とは空と海が接する線で、文字からするとまっすぐ、水平であるべきですが、地球が
丸いため、実際の水平線は曲がって見える・・・と。
すなわち、「水平線を眺めると地球が丸いのが分かる」という表現は、ある程度正しいですが、
条件が伴うのです。
肉眼で見た際、地平線や水平線がわずかに湾曲していることを感じることができるのは、高い
場所にいる場合や、広大な水面を見ているときです。例えば、飛行機の高度や、高い山、
あるいは海上などの広い場所であれば、地球の丸みを実感しやすいです。
ありません。
よって、 地球の丸さを水平線を見て完全に理解するのは難しい ものの、特定の条件下では湾曲が
感じられるため、部分的には正しいと言えます。すなわち、 地球の水平線の湾曲を肉眼で
感じられるのは、約10,000メートル(10km)以上の高度に達したとき です。この高度に
達すると、水平線の湾曲が肉眼でもはっきりと見えるようになります。一般的な旅客機の
巡航高度(約10,000メートル~12,000メートル)では、機窓から水平線・地平線が
湾曲しているのが確認できることがあります。
一方で、山や建物の上から地平線・水平線を見ても、通常はその湾曲を感じ取ることは難しく 、
飛行機のような高度が必要です と。
下の写真の如き場所からは、水平線は直線にしか見えないので、水平線・地平線が湾曲している
のは確認できないと。
下の写真の水平線上に、 青い直線ーーーー を引いて見ました。

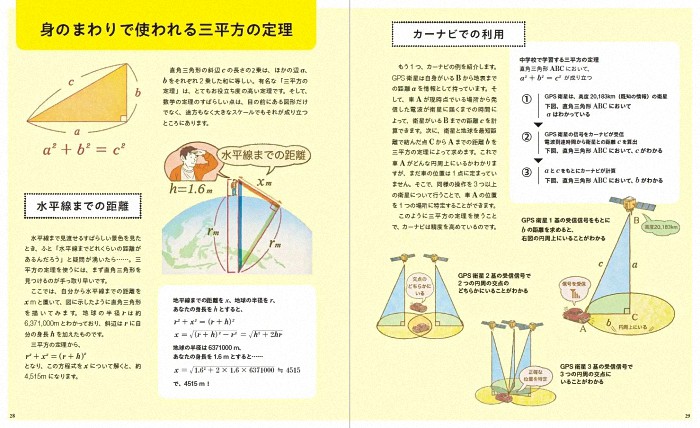
写真の右の水平線に沈んで行く船は海岸からどのくらい離れているでしょうか?

そして 水平線に浮かぶ街並みはどのくらい離れた場所 ?。

光は直進 しますから水平線より下は見えません。 A点から見れば遠くの船ほど上部しか
見えないのは 地球の曲率によって見えなくなると昔の人は既に考えていた とのこと。
また周囲を海で囲まれた島の高い山に登って四方をみわたせば、なんとなく地球が丸いことを
感じる事ができたのです。船乗りなど漠然とではあっても知っていたはずなのです。
皆既月食の時、月に写る地球の影が丸い ことから地球が丸いことも知っていました。

さて、この日の学習テーマに戻りますが、
人が海岸線に立ち、そこから見える水平線までの距離 は、 目の高さがわかれば計算することが
できる のです。
地球は丸いので、その断面は円で近似することができます。 その円の半径をrとして、図のように
地面から高さhのところに目の位置があるとしましょう。そして、そこから見た水平線
までの距離をxとすると、xは目の位置から地球に引いた接線の長さになります。
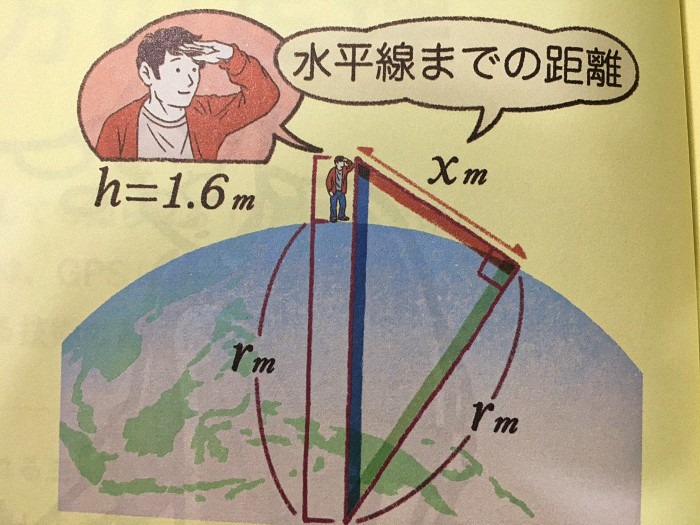
地球の半径rを6371000m、海岸に立ったときの海面からの目の高さが
h=1.6m(目の高さ)とすると、下記の如き計算となるのです。
下図の如く『 三平方の定理 』から計算します。
そしてx=4515m= 4.515km となります。
「 水平線の彼方 」と言うほどなので、はるか遠いイメージがあるかも知れませんが、
たった 4.5km先しか見えていない のです。みなさん、もっと遠く数十km先と思っていた
のでは!!もしも、 自転車で海の上を進めるとしたら20分で着くくらいの距離 なのです。
丘の展望台などに立って、 海面から150mの高さに目を置いて海を見ているという場合は、
目の高さが100倍になりますから、水平線までの距離は10倍の45.15km となるのです。

この 船舶の動画
👈️リンクは、見えている水平線の僅か遠方を航行しているものです。
船の下部は隠れており、上部のみ見えています。
さらに水平線の先を航行する船舶。
船の最上部しか確認できません。
江戸時代に歌川広重によって描かれた浮世絵「 冨士三十六景伊勢ニ見か浦
」が下の絵。
水平線のはるかかなたに富士山が描かれています。
描かれているのはいいとして、これを描いた場所が問題なのです。
約4.5km先しか見えないはずの水平線に、富士山が見えるわけがない?。
ということは、歌川広重は、想像で富士山を描いたのでしょうか。

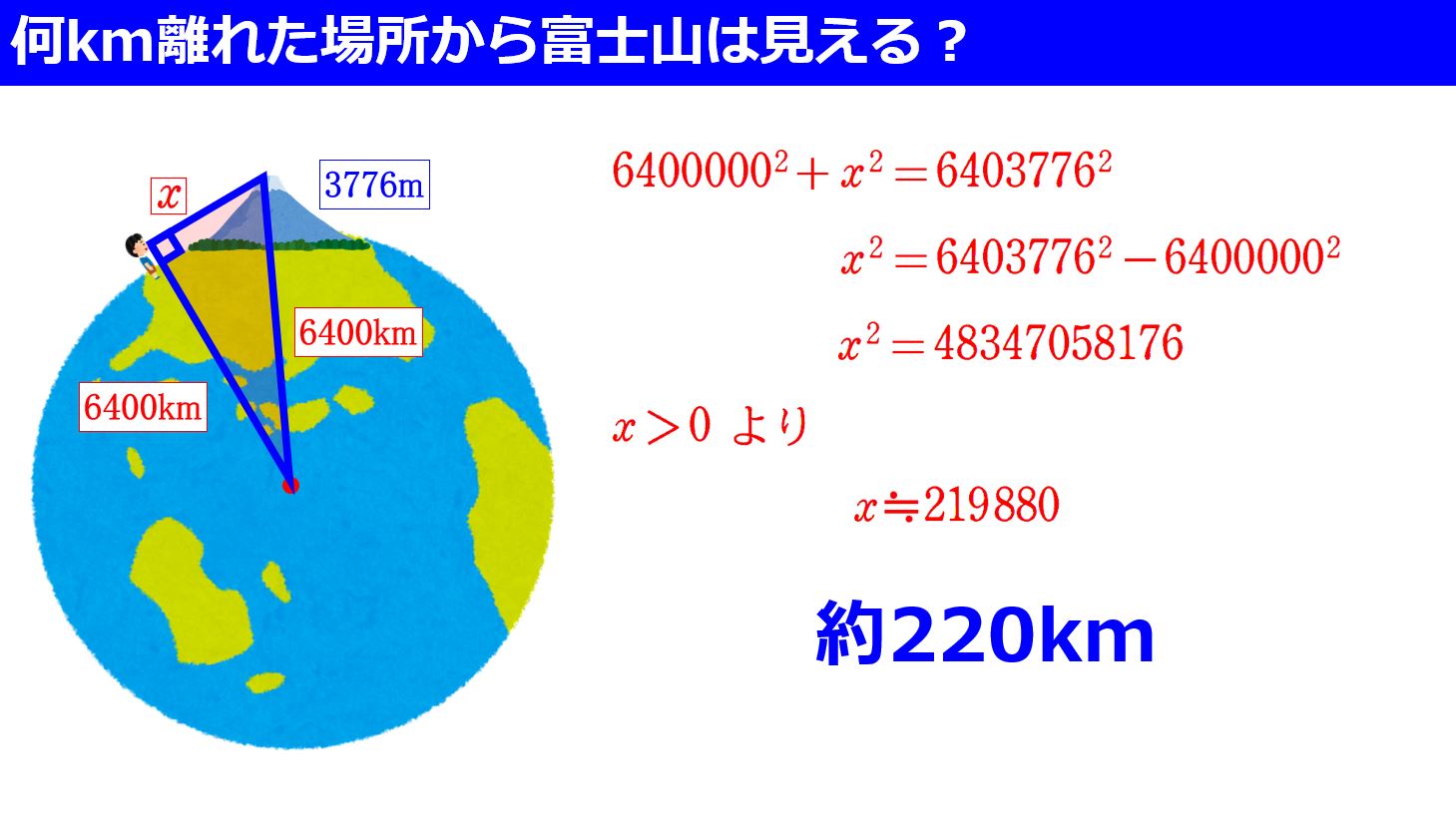
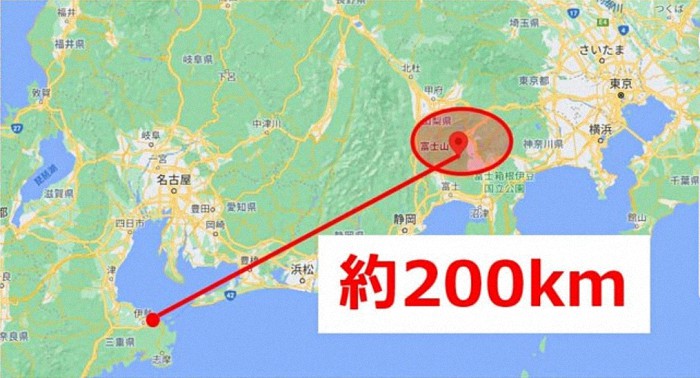
ところで「 何km離れた場所から富士山は見える? 」👈️リンク
計算の結果は、 約220km以内であれば富士山は見える と。
そして、三重県伊勢市の二見浦。
富士山までの距離は、約200km !!。
よって、 浮世絵の富士山も想像ではなく、実際に見えていたのだと推測 できるのだと。
逆に言うと、 富士山の頂上から見れば、計算上では、三重県の二見浦まで見える ということ。
高さが高ければ高いほど、遠くまで見えるということなのです。
当たり前のような話ですが、遠くまで見える距離が一気に伸びるのです。
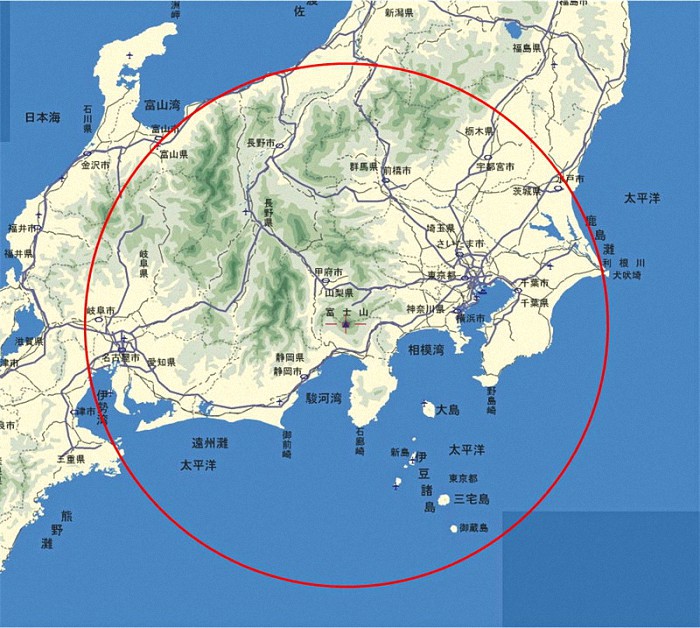
下図が、理論上、富士山頂から見える日本国内の範囲
です。
纏めて見ます
と
●始めに登場した 自分の1.6mの目の高さからは、4.5km
● 富士山の3,776mだと、約220km
● 東京スカイツリーの展望台の450mだと、約76km
まで見えるようです。
これは、富士山の麓くらいまでの距離。
● 世界一のエベレスト。8,848.86mだと、約337km
まで見える。
ちなみに、日本までの距離は4,000km以上。よって全然見えない!!。
世界一とはいえ、地球の丸さには勝てないわけです!!。
● 上空10,000m、飛行機の機窓からは約380km
羽田空港上空10,000mからは名古屋くらいまで見えるということです。
スカイツリーから見える富士山の姿
をネットから。
ケータイやカーナビなどでは、さまざまな方法を利用して位置情報を取得しているのだ。
次にその仕組みを見ていきましょう。
その中心になるのが GPS(Global Positioning System/汎地球測位システム)。
「もう1つ、カーナビの例を紹介します。
「 GPS衛星
」👈️リンクは自身がいるBから地表までの距離aを情報として持っています。
そして車Aが現時点でいる場所から発信した電波が衛星に届くまでの時間によって衛星がいる
Bまでの距離cを計算できます。次に、衛星と地球を最短距離で結んだ点CからAまでの距離bを
三平方の定理によって求めます。これで車Aがどんな円周上にいるかわかりますが、まだ車の
位置は1点に定まっていません。そこで同様の操作を 3つ以上の衛星について行うことで車Aの
位置を1つの場所に特定
することができます。
このように 『三平方の定理』を使うことで、カーナビは精度を高めている
のです。」

4機以上の衛星で衛星測位は可能ですが、安定した位置情報を得るためには、より多くの衛星が
見えることが望ましいです。しかし、GPS衛星は 都市部や山間部ではビルや樹木などに電波が
遮られて可視衛星数が減り、位置情報が安定的に得られない
ことがあります。
2018年11月から、「 みちびき・QZSS(Quasi-Zenith Satellite System)
」は4機体制で
運用を開始しており、このうち3機はアジア・オセアニア地域の各地点では常時見ることが
できます。みちびきはGPSと一体で利用できるため、安定した高精度測位を行うことを可能と
する衛星数を確保することができます。GPS互換である「 みちびき・QZSS
」は安価に受信機を
調達することができるため、地理空間情報を高度に活用した位置情報ビジネスの発展が期待
できます と。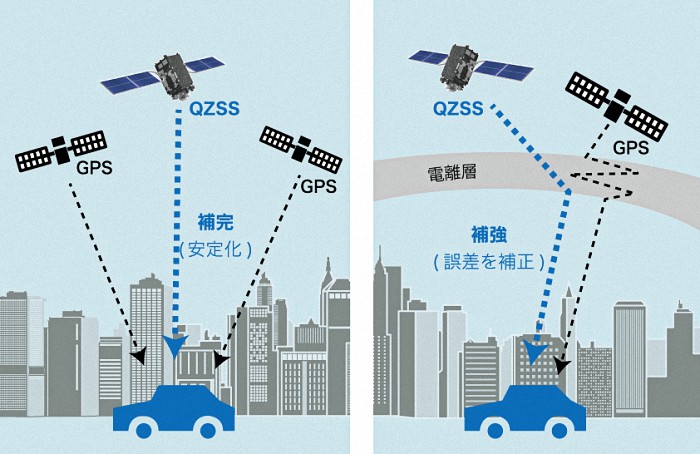
順序が逆になりましたが、
ところで『 三平方の定理
』とは、
2辺の長さをa、b、斜辺の長さをcとする直角三角形において成り立つ、次の定理です。
斜辺cの2乗は、他の辺a、bをそれぞれ2乗した数の和に等しい
のです。
直角三角形では、2つの辺の長さがわかると、三平方の定理を使って他の1辺の長さが計算できる
ことを覚えていますか??
また、三平方の定理の逆も成り立ちます。3辺の長さがa,b,cの△ABCにおいて、
a^2+b^2=c^2が成り立つならば、△ABCは直角三角形である
ということも言えるのです。
※「^2」は自乗・2乗の意味。

この『 三平方の定理 』は下記のごとく証明できるのです。
まず、三角形の内角の和は180°=90°+x°+y°
内接する小さな正方形の赤く示された角度 ┓ +x°+y°=180°なので
=180ー(x°+y°)=180°-90°=90° よって 内接する四方形も正方形 なのです。
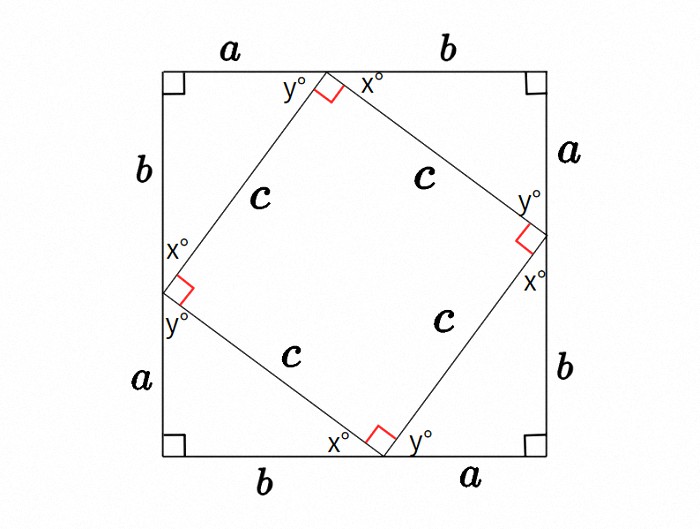
中の正方形の面積を計算しますと『三平方の定理』が導けるのです。

そして、 昔の人はどのように地球の大きさを求めたか?
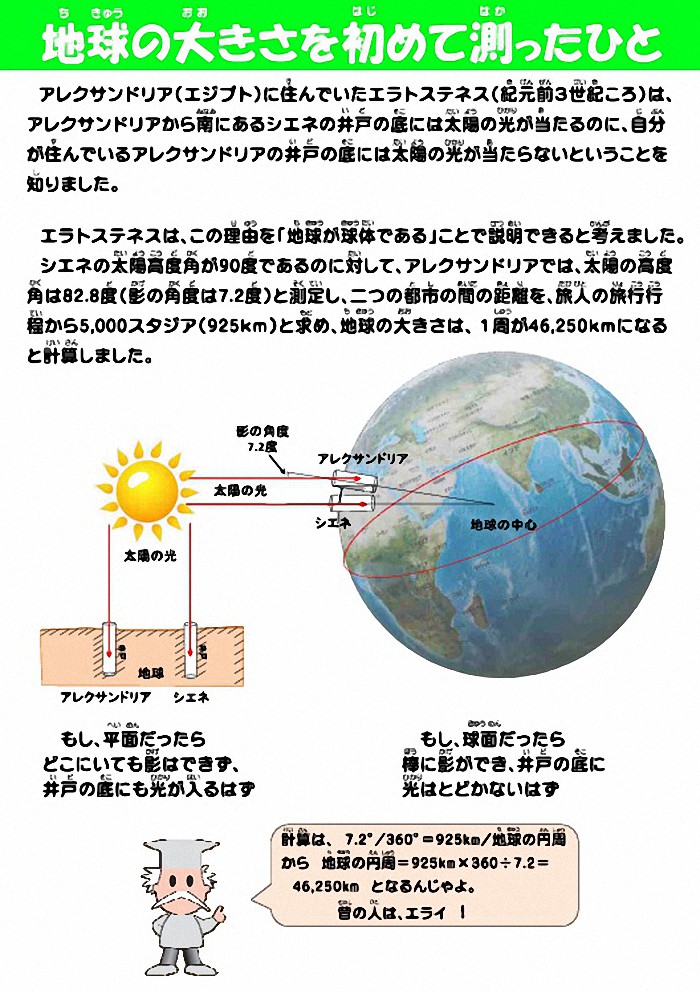
「 地球の大きさを初めて測ったひと
アレクサンドリアから南にあるシエネの井戸の底には太陽の光が当たるのに、自分が
住んでいるアレクサンドリアの井戸の底には太陽の光が当たらないということを知りました。
工ラトステネスは、この理由を「地球が球体である」ことで説明できると考えました。
シエネの太陽高度角が90度であるのに対して、アレクサンドリアでは、太陽の高度角は82.8度
(影の角度は7.2度)と測定し、ニつの都市の間の距離を、旅人の旅行行程から5,000スタジア
( 925km )と求め、地球の大きさは、1周46,250kmになると計算しました。」
繰り返しになるが、さらに詳細を。
キャラバンが50日かかって歩いていたことから、シエネからアレキサンドリアまでの
距離を求めた。
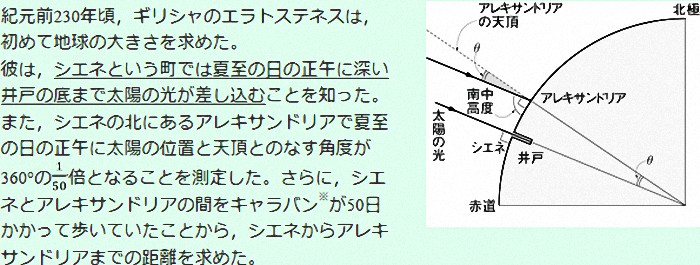
シエネからアレキサンドリアまでの距離は925kmとなることから
地球の全周は46250kmと。
よって地球の半径は7400kmを導き出したと。
ウィキペディアによると地球の半径: 6,371 kmである ので、 誤差約16%の精度 で
紀元前でも算出していたのであった。

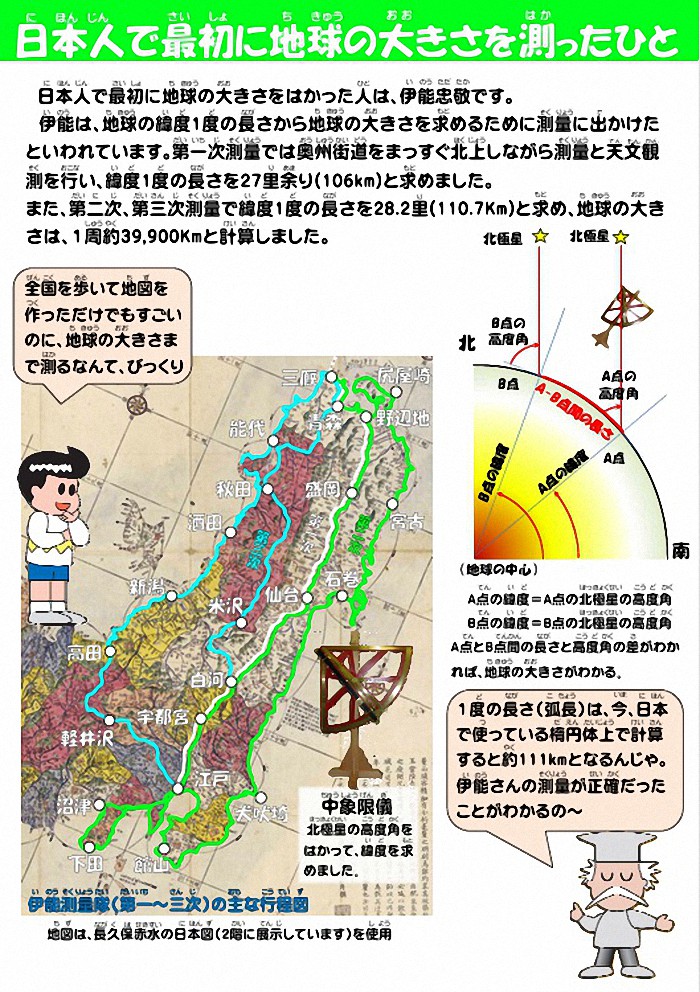
「 日本人で最初に地球の大きさを測ったひと
います。第一次測量では奥州街道をまっすぐ北上しながら測量と天文測量を行い、緯度度1度の
長さを27里余り(106km)と求めました。
1周約39,900Kmと計算 しました。」
北極と南極を通るように南北に一周する場合で約40009km となり、少しだけ赤道の方
よって 約220年ほど前に伊能忠敬は、99.5%の精度で測量 していたことになるのだ。
そして最後に、 月面から「地球の出」 の写真を。
「地球の出」とは、月の地平線から、地球が上ってくるようにみえる現象をいいます。
月の自転周期と公転周期は同じなので、月はいつも同じ面を地球に向けています。
これは逆にとらえると、 月の表側のある地点に立って地球を見た場合、いつも同じ場所に
地球が浮かんでいるように見えることになります。 月の表側の真ん中付近ではいつも頭の真上に
地球は見えますし、月の南極や北極、裏に近い端の方では月の水平線上に見えるでしょう。
このため、南極や北極を飛行している宇宙船から、月の地平線上に地球が出てくる「地球の出」
や、逆に地球が地平線の下に消えていく「地球の入り」をみることができるのです
と。
月周回衛星「かぐや(SELENE)」が2008年9月30日、「 満地球の出 」 👈️リンクの撮影にも成功。

そして「 満地球の入り 」👈️リンクも
・・・ つづく ・・・
-
小田原城下を歩く-3(その60):妙泉寺 2024.11.28
-
小田原城下を歩く-3(その59):徳常院~妙… 2024.11.27
-
小田原城下を歩く-3(その58): … 2024.11.26










