受験数学って暗記！？(仮)～高校受験・大学受験～

無限級数～別解～

サッカー少年さんから頂いたコメントを元に無限級数の問題の別解を作ってみました．もう一度問題から．予備知識としては次の「ド・モアブルの定理」．思考の過程が分かるように解答ではなく，解説を書きます．ここまでくればあとは簡単．余計なものまで求めたから長くなってしまったが・・・これで良いのかな・・・？ド・モアブルの定理って複素数平面をしなくなったから現行過程では習わないか．う～ん・・・まぁ良いか・・・（笑）せっかく書いたのでアップ！サッカー少年さん，ありがとうございましたm(_ _)m

部分分数分解 その3

部分分数分解を速くする方法の第3弾です．(第1弾と第2弾を読んでから読んでください)分母に1次式の3乗を含む場合の部分分数分解の方法の解説をします．※3乗以上でも同じ方法で対応できます．

部分分数分解 その2

部分分数分解を速くする方法の第2弾です．以前は分母が異なる1次式の積になっている最も簡単な場合の解説をしました．今回は分母に1次式の2乗を含む場合の部分分数分解の方法の解説をします．※係数比較以外の方法で，bを求めるには分数関数の微分法(数3)を知らないといけません．a,cは前と同じように求めることができます．bはcを求める式を微分してから代入すれば求めることができます．※分母に1次式の3乗以上の式を因数に含む場合も同じですが，係数に気をつけないといけません．これについてはまた別の記事にしたいと思います．練習問題をつけておきます．答えはコメント欄に書きます．

無限級数

基本は「第n部分和をnで表し，n→∞として極限を求める」方法．kの値を1から1ずつ増やしていくと，cos(k-1)π/4の値は1，1/√2，0，-1/√2，-1，-1/√2，0，1/√2，1，・・・と周期8で変わっていく．したがって，まずは考えやすい「n=8m (m=1，2，3，・・・)の場合」を考え，それぞれの値で分けて部分和を求める．なんか分かりにくい表現だ・・・お許しを・・・それでは解答～式が長くて嫌・・・もっとスッキリした解答があるような気がする．

漸化式～nの1次式が付いてるタイプ～

今回は後ろにnの1次式がついているパターン．前にも書いたけど，左辺を「n+1 に関する式」，右辺を「n に関する式」にすればよい．つまり，4n-1 を上手い具合に両辺に分けることができればいいってこと．nの1次式を両辺に分けることを考えるから，右辺の「n に関する式」は「αn+β」とおくことにする．左辺は「n+1 に関する式」を考えないといけないからどのようにすればよいか？「αn+β」が「n に関する式」だから，それに対応する「n+1 に関する式」は「α(n+1)+β」となる．つまり「n」を「n+1」に変えれば良いってこと．それでは解答．後ろにnの1次式がついているパターンの解法を示したが，後ろについてるのがnの2次式や3次式であっても同様に解ける．例えばnの2次式がついているようなというタイプなら，とおいて係数比較をすることにより，α，β，γを求めればよい．

漸化式～n乗のタイプ～

漸化式特集の続き．今回は後ろに「n乗」がついてるパターン．ここで「n乗」って書いてるけど，別に「n+1乗」でも「n-2乗」でも構わない．n乗に関連するものならすべて同じパターンだ．それでは次の例題を使って説明する．この「後ろがn乗の形」になっているときの処理方法は決まっている．両辺を 2^{n+1} で割れば前のパターンに変形することができる．また次のような考え方もある．要するに左辺が「n+1に関する式」，右辺が「nに関する式」にすればよい．つまり 5・2^{n-1} を両辺にうまい具合に分けることができれば問題ないということだ．

反比例の変化の割合

まさとさんからの質問にお答えします．コメントで頂いた質問ですが，結構古い記事へのコメントだったため，記事で回答させていただきます．＜質問内容＞今日、子供に反比例の変化の割合ってあるの？と聞かれました・・・・私としては、一定の割合で変化する物と考えると、あえて考えるなら・・・２次関数のように点と点を直線で結び、その傾きと考えたらいいのかと思う気持ちと、またはとぎれていることと、著しい変化の違いがあることから、変化の割合じたいがないのでは？？？という気持ちがあります。よければ教えてください。＜回答＞僕自身，反比例の変化の割合というものを考えたことがありませんでした．変化の割合は「ｘが増える量に対してｙがどれくらい増えるかを表したもの」と定義されています．反比例の場合，ｘ＜０の部分とｘ＞０の部分にグラフが分かれています．このような場合に変化の割合を考えるなら，ｘ＜０の部分とｘ＞０の部分に分けて考えなければならないと思います．y=1/xにおいてｘが２から５まで変化するときの変化の割合について考えると・・・（ｘの増加量）＝５－２＝３（ｙの増加量）＝1/5-1/2＝-3/10となるため，（変化の割合）＝-3/10÷３＝-1/10 と求めることができます．ｘの変化する範囲がｘ＜０の部分のみ，またはｘ＞０の部分のみならば上記のように計算することができます．しかし，ｘがｘ＜０の部分からｘ＞０の部分へ変化するときの変化の割合は，単に数値だけの計算なら可能ですが，求めた数値に意味はないと思います．しかもｘをｘ＜０の部分からｘ＞０の部分へ少しずつ変化させるとわかりますが，ｙ軸の部分で途切れているため変化させることができません．ということで僕の考えは，ｘ＜０の部分やｘ＞０の部分に分けて考えるなら反比例の変化の割合を考えるのもアリだと思います．

閃きが話題になってる♪

Dr.NERO先生のコメント欄にも書いたけど，こっちにも書いておこう．別解が豊富な問題ほど「解く価値」があると思う．逆にいくら「テクニカルな手法」であっても，その問題でしか使えないような手法ではその問題を解く価値があまりないと思う．ここから追記．いわゆる「閃く」ためには，既存の解法パターンを「常識」として頭の中に保存していつでも取り出せる状態にしておかなければならない．ネジとドライバーを例にとって話してみよう．今目の前に一つのネジがある．そして用意されてるドライバーは1本．この場合はそのドライバーを使わざるを得ない．もしそのドライバーが使い物にならないくらい合わないものであれば，ネジを締めるのを諦めるしかない．あるいは手である程度まで無理矢理締めるくらいしか出来ない．ある程度ネジを締めることができたら部分点GETと言った感じか．それではドライバーが5本用意されていたらどうなるだろうか？ネジを目で見て大きさを確認した後，ドライバーを手にすることになる．初めは大体これがちょうどいい大きさだろうと思って手にする．しかし微妙に合わないことがある．仮にドライバーが小さかったとすると，次は必ず大きいドライバーを選ぶはずだ．少しでもピッタリ合うドライバーを使っていく．そして持っているドライバーの中にネジにピッタリ合うものがあればそれでネジを締めることが出来る．これが完答できた状態だろう．あと変わった方法としては，ドライバーの他に道具を持っていて，持っているドライバーに合うように「ネジやま」自体を変えてしまう方法がある．ある意味反則的手法であるが，ネジ自体を変えてしまうというのは賢い方法であると言える．この状態が「そんなの思いつかない！」という「テクニカルな手法」？ネジ自体を変えるなんて思いもよらない発想かもしれないが，1回見てしまえば次に困ったときにも「過去にこんな方法があったな」とネジ自体を変えることを考えるかもしれない．そしてそれがうまく行った場合，その方法を知らなかった人が見れば「なんてすごいんだ！それは思いも付かない！すごい閃きだね♪」となるのではないだろうか？ネジを締めるためにはドライバーを一杯持ってれば明らかに有利だし，ネジとは結びつかない道具ももしかしたらネジ自体を変えるのに使えるかもしれない．もう分かるとは思うが，ネジとは「問題」のことで，ドライバーや他の道具とは「公式や知識・解法パターン」のことである．色々と試行錯誤できるように道具は一杯持っておくにこしたことはない．ただし，その道具を腐らせてはいけない．いつでも使えるように磨いておくことが必要だ．せっかく手に入れた素晴らしい道具でも1回使ったきり，全く使わず引き出しの奥で埃をかぶっているような状態では非常に勿体無い．今学校や塾で教えてもらっている公式や知識・解法パターンは一つ一つが問題を解くための素晴らしい道具になる．一つ一つその道具を大切にして，いつでも使えるように磨いておこう！更には，道具の組み合わせによっては別の力を発揮できるものもある．そういうことを考えるのも面白いかもしれない．こんな風にゲームっぽく考えると数学も面白くなるのではないだろうか？ん～～ならないか・・・(笑)またダラダラと書いてしまった・・・

受験数学には閃きは必要か？

そもそも「閃き」とは何なのか？閃きの定義について検索したけど，はっきりとこうってのが見つからない．調べ方が甘いのかもしれないけど・・・仮にひらめきとは「人が思いつかないような解法を思いつく」ということにする．ここで「人が思いつかない」とあるが「どれくらいの割合の人が思いつかなければそう判断されるのか？」ということも問題である．100人に1人しか思いつかないようなことなら閃きと判断されるのか？1000人に1人しか思いつかないようなことなら閃きと判断されるのか？数学の場合，人が思いつかない解法は習っていないものと決め付けることができる．もし学校などで習う解法であれば，大抵の人が「思いつく」ことになり，「閃き」とは言わないだろう．というか人が思いつかない解法というのはあり得ない．入試問題は解けることが前提で作られていて，必ず少なくとも一つの解法が存在する．既に解法が存在する以上，人が思いつかない解法ではない．未解決問題を入試問題として出題した場合，それを解くためには「閃き」が必要だと思うが・・・ということで閃きの定義を変えてみよう．閃きとは「人が思いつかないような解法を思いつく」ではなく，「問題を見て解法に至るまでの過程を思いつく」ということにしよう．問題と解法を結びつけるものが見つからなかったときに，「そんなの思いつかない！閃かない！」となるのではないだろうか？また，問題と解法を結びつけるものが見つかったときに，「思いついた！閃いた！」と言ってるのではないだろうか？しかし，その問題と解法を結びつけるものを知ってる者から見れば「当たり前の思考の流れ」であって決して「閃いている」わけではない．今までの経験に基づいて考えた結果，解法に行き着いたというだけで，「そんなの閃かない」と言ってる人を見て「それはその人が知らないだけ，単なる経験不足」と判断を下すだろう．ある問題に対して正解となる思考の過程が偶然に生まれることはない．まずは今まで解いてきた膨大な量の問題と今解いている問題を比較し，似ている問題を脳内検索する．その検索結果として出てきた問題の解法を次々と当てはめると言った「試行錯誤」をし，いくつかがその問題に合った解法にたどり着く．「経験豊富な人」はその一連の動作が高速で行われるため，問題を見た瞬間に手が動くという「経験不足の人」にとっては不思議な現象が起こるのではないだろうか？したがって，一般に言われている受験数学における閃きとは・・・「偶然の出来事ではなく，情報の蓄積と結びつきの結果」ではないだろうか？ただ，こういう定義をしてしまうと，僕のブログのタイトルを「受験数学は閃きだ！」に変えないといけない．すべての問題において「閃き」が必要となるからだ．一般に言われる「閃き」とはそういうものではなく，「偶然の出来事」のように扱われてるような気がする．しかし，厳密に「閃き」の定義が分からないので，ブログのタイトルは「受験数学って暗記！？」と「？」を付けている．あとは「暗記」もどこまでを「暗記」というかも問題になってくる．僕が言う「暗記」は「単純暗記」ではなく「理解を伴う暗記」である．そんなの暗記と言わないと言われればそうなるだろう．「理解を伴う知識の蓄積」とでも言うしかないだろう．ブログのタイトルが「受験数学とは理解を伴う知識の蓄積だ！」と書いても当たり前すぎて誰も見ない気がする．ということで「暗記！？」となっている．要するに，自分でも何が「閃き」で何が「暗記」と言われるものなのか分かっていないということ．なんだそれ？全然まとまってないやん・・・(笑)とまぁこんな感じです．いかがですかシンバ先生？

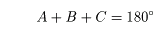
平面図形の証明

[問題]半径が1である円がある．その円に内接する三角形の各辺の2乗の和が8より大きいとする．このとき，その三角形は鋭角三角形であることを証明せよ． 今回は(も？)僕が考えた順番に書いていきます．つまり僕の思考回路の曝け出しってことですね．う～ん・・・恥ずかしい．（今更何を言ってるのか・・・）と冗談を言ってる暇はない・・・ではいきます！まずは扱う三角形を△ABC（3辺の長さは a,b,c）とする．この時点で一つの条件式が作られる．当たり前の式であるが忘れないようにしよう．それでは条件を式で表そう．△ABCが半径1の円に内接している，つまり△ABCの外接円の半径が1．「外接円」とくれば使うものは「正弦定理」！ということで次式が得られる．さらに「△ABCの各辺の2乗の和が8より大きい」をそのまま不等式で表すと次のようになる．以上の3つの式が問題文の条件である．次に示すべきことを式で表すことを考える．示すべきことは「△ABCが鋭角三角形」ということだ．鋭角三角形とは何か？3つの角がすべて鋭角である三角形のことだ．条件文を式で表したことからsin，cosで表すことは予想できる．sinは鋭角でも鈍角でも正で変わらないから符号が変わるcosを使おう．「 cosA>0　かつ　cosB>0　かつ　cosC>0 」この状態ではまだ「かつ」という言葉が残っているので消して1つの式にすることを考える．3つの数がすべて正だから，3数を掛けても正（原則として和ではなく積を考える）ってことで出てくるのは次の式である．「 cosAcosBcosC>0 」しかし，一つの疑問が生じる．逆が成り立つかどうかという疑問である．3数を掛けて正だからと言って，3数すべてが正であるとは一般には言えない．しかし，今扱っているのは単なる3つの数ではなく，三角比である．cosAcosBcosC>0 が成り立つ例として，仮に 「 cosA>0,　cosB0 かつ cosB>0 かつ cosC>0 ⇔ cosAcosBcosC>0が成立することが分かり，示すべきことを式で表すことができた．ちなみにこのこと自体は僕の中では公式となっている．色々な問題集に証明問題として載っているので，いつでも出来るようにしておこう！さて，話を戻します．あとは条件からこの不等式を導くだけ！ということで初めの問題は次のようになる．とりあえずは a, b, c を消去し，次数を2次から1次に下げる．その後，和積の公式を使い，積の形に仕上げていくという感じ．上記の解答で解説は終わりだけど，ついでなので証明を載せておこう．

漸化式～特性方程式～

前回の問題において，右辺を展開して同類項整理すると次のようになる．実際見かける問題もこの形になっていて，前回のような形では出題されない．この漸化式を解くためには，変形する前の状態（前回の問題の形）に戻さなければならない．どのようにして変形するかがポイントとなる．与えられた漸化式がと変形できたとしよう．(a_n の係数は 2 だから，その部分は変えない)「+1」という定数を上手い具合に両辺に振り分けてやるのだ．ここで注意することは，左辺が「n+1 に関する式」右辺が「n に関する式」と添え字を一つだけずらした「同じ形」でなければならない．それではこの式を展開・整理すると，となり，係数比較によって c=-1 となることが分かる．したがって，この問題は前回の問題と変形でき，解けることが分かる．では，この定数 c を求めるために，いちいちとおいて係数比較をしなければならないのか？という疑問が生じる．そこでよくあるのが，次に示す特性方程式を用いて求める方法である．この説明をすると，ほぼ確実に次のような質問を受ける．「a_{n+1} と a_n は違うものなのに，同じ文字でおいても良いのですか？」確かに異なる値をとるものを同じ文字で置いてしまうところが納得いかないだろう．それでは考え方を変えてみよう．「そもそもこの定数 c にはどのような意味があるのか？」この問題では c=-1 である．では，数列{a_n}の初項を -1 と仮定しよう．つまり次のような問題を考える．この場合の一般項はどうなるだろうか？n = 1, 2, 3,・・・のときを実際に計算すると次のようになる．上の計算からも分かるように，数列{a_n}の一般項は a_n=-1 となることが分かるだろう．つまり，a_{n+1}=a_n となるような a_n の値が -1 だったということで，同じ文字において方程式を解けばその値が得られることも分かるだろう．-1 は特性方程式の解であるから，-1=2・(-1)+1 を満たす．この等式と元の漸化式から次のように変形することができる．これで解けるはず．答案には特性方程式によって -1 を求める過程を書く必要がない．したがって，解答は次のように書けばよい．

漸化式～基本形～

まずは漸化式の基本形から．上が等差数列だと判断できる形．下が等比数列だと判断できる形．しっかり理解してこの形になればすぐに一般項を求められるようにしよう．では問題．左辺と右辺の括弧内が「同じ形」であることに注意．違いは左辺が「n+1 に関する式」で右辺が「n に関する式」となっていること．分かりやすくするために置き換えてみよう．次のことが分かるかな？分かりにくければ次のように n=1,2,3,・・・の場合を考えてみよう．つまり，a の添え字と b の添え字が等しいってこと．数列 {b_n} で置き換えた場合，初項は b_1=a_1+1=2 だから，与えられた漸化式は次のようになる．こうなれば「等比数列を表している形」だと分かるよね？ということで解答は次のようになる．一般項を求めた後は，n=1のときの値を求めて，a_1と初項が一致することを確かめておこう．もし一致しなければ，どこかで間違っているので見直そう．見直した結果，どこにも間違いがなかった場合，考えられるのは次の2つ．[1] 確認のために求めた a_1 の値が間違っている．（確認の計算間違い）[2] 問題を見間違えている．どちらにせよ，単なる「ケアレスミス」「つまらないミス」では済まされない．masa/k先生が書かれているようにそれが実力だと思うようにしないといつまでもミスはなくならない．1問1問丁寧に解く癖をつけよう．

2006年 神戸大・文系

高1の授業で少し説明したので具体例を挙げておきます．この問題を見て「点Pってどこ？っていうか『点Pを通る直線 l_t はただ1つであるとする』の意味が分からない！」となってどうしたらいいのか分からなくなる人がいると思う．数学の問題は「～のとき，・・・を求めよ」となっているものが多い．言うまでもなく，条件や求めるべきものをしっかりと理解することが大切．条件が数式で表されている場合はまだ楽．言葉で表されている場合は，その言葉が表す内容を普通は数式で表して解くことになる．また，求めるべきものも数式ではどういうものを求めるのかということを知っておく必要がある．それでは一つ一つ整理していこう．この問題で求めなければならないのは「点Pの軌跡」．点Pは直線・放物線・円・楕円・双曲線や3次関数などの何かしら曲線を描くわけで，「その方程式を求めなさい」と言われている．「軌跡を求めよ」と言われれば，通常は，軌跡を描く点の座標を(X,Y)とおいて，X,Yの満たす関係式(方程式)を求めることになる．ということで，点Pの座標を(X,Y)とおくことにする．では次に条件とされている「点Pを通る直線 l_t はただ1つであるとする」について考えよう．とりあえず「ただ1つである」という部分は一旦無視して考える．「点Pを通る直線 l_t」は「直線 l_t は点Pを通る」と言い換えることができる．つまりは点Pの座標を直線 l_t の式に代入すると成り立つということ．実際に代入すると，Y=2tX-t^2 となる．では「ただ1つである」の部分について考えよう．何がただ1つ，言い換えると何が1つしかないかというと，「直線 l_t が1つしかない」のである．では直線 l_t は何によって決まるのか？問題文にもあるように「実数 t」の値が決まれば，それに応じて直線 l_t が1つだけ決まる．「直線 l_t が1つしかない」ということは，「実数 t が1つしかない」と言ってるのと同じことである．つまり「Y=2tX-t^2 を満たす t が1つしかない」のである．Y=2tX-t^2 は t についての2次方程式と見ることができるから，「t についての2次方程式 t^2-2Xt+Y=0 がただ1つの実数解をもつ」ということである．ここまで言い換えればもう分かるよね？2次方程式がただ1つの実数解をもつ条件について考えればよく，それは判別式が0ということだ．以上のことを踏まえて解答を書くと次のようになる．ちなみにこの問題は「包絡線」に関した問題．包絡線とは・・・与えられた曲線族と接線を共有する曲線，すなわち与えられた（一般には無限個の）全ての曲線たちに接するような曲線のことである．

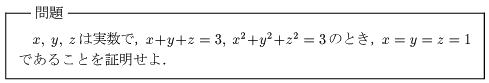
再び等式の証明～第6弾～

この等式の証明では，条件が式で与えられていて示すべきものも式で与えられている．しかし，示すべきものは1本の式とはいえない．「x=1 かつ y=1 かつ z=1」と書けば分かるように「かつ」という言葉でつながれている．その部分にこの証明の難しさがある．ということは，示すべきものを「かつ」を使わずに1つの等式で表すことができればかなり楽になる．問題を単純化してみよう．「x=0 かつ y=0」 を1つの等式で表せ．この逆の操作はかなりやっていると思う．それは「実数の性質」でやっているはず．元に戻してみよう．「x=1 かつ y=1 かつ z=1」基本的には「0」と等しくなるようにしたほうが良い．ということで書き換えてみよう．「x-1=0 かつ y-1=0 かつ z-1=0」これで分かるかな？つまり，問題は次のように書き換えることができる．ここまでくれば，左辺を計算していって，条件を使うことによって0になるということを示せばいいことが分かる．

二項係数～式が表す意味～

さっきの記事の続き．もう一度問題を表示しておく．ただ計算して証明できてもイマイチという感じ．ということで，この式がどういうものを表しているかを考えてみよう．いつもは「言葉で表されたものを式で表せ」と言ってきたが，これは全く逆の操作．とりあえずは「なるほど．そう捉えることも出来るね．」と軽く捉えてもらえばいいと思っている．突然であるが，次の問題を考えることにしよう．n 人の中からリーダー1人を含む k 人を選ぶ方法は何通りあるか？この問題を解くために，次の2通りの方法で考えてみる．(i) n 人から k 人を選んだ後で，その中からリーダー1人を選ぶ．(ii) n 人からリーダー一人を選んだ後で，残りの n-1 人からリーダー以外の k-1 人を選ぶ．それぞれの場合の数を考えるんだけど，その際に必要なのが次の「積の法則」．それではそれぞれの方法について．(i)の方法を考える．n 人から k 人を選ぶ方法は nCk 通り．その選んだ k 人からリーダーを1人選ぶ方法は k 通り．積の法則によって，等式の左辺が得られる．(ii)の方法を考える．n 人からリーダー1人を選ぶ方法は n 通り．残りの n-1 人からリーダー以外の k-1 人を選ぶ方法は (n-1)C(k-1) 通り．積の法則によって，等式の右辺が得られる．(i)と(ii)は考え方が異なるだけで，「n 人の中からリーダー1人を含む k 人を選ぶ」ことに変わりはないので等しいはずである．ということで等式が成り立つことが証明された．このような具体例を挙げることにより，一見無意味な等式にも意味があることがわかるだけでなく，単なる計算のみの証明だけでは与えられない「なるほど感」を与えられると思う．

二項係数～頻出問題～

今回は二項係数の性質としてよく出題される問題について．等式の証明の問題．この場合，両辺をともに同じ形になるように変形して等しくなることを示せばよい．ってことで解答です．これで証明はできているけど，生徒の反応はイマイチ．「分かるけど，何これ？計算させたいだけ？」と言った感じ．ではどうすれば良いだろうか？

2次方程式の重解について

今回は2次方程式が重解をもつ条件とその解について書きます．問題自体は難しくないですが，よく質問されるので書いておこうと思いました．まずは2次方程式の解の公式．次に判別式について．判別式って単に「解の公式の根号の中身」ってことだからね．そして，よくされる質問とは・・・「重解が x = -b/(2a) となるのが分からない」解の公式と判別式の関係をしっかり理解しておこう．重解をもつということは，判別式が0になる．つまり，根号内が0になるということ．どうも忘れやすい事項みたいなので，しっかり理解して使えるようにしよう！最後に解答です．計算の途中の掛け算はわざと計算してません．両辺を9で割るのも楽だし，どっちにしろ，素因数分解して根号の外に出せるものは出さないといけない．それなら計算するだけ時間の無駄ってこと．掛け算の形になっているんだから，その形を最大限利用しよう．この問題ではたまたま4の2乗になったが，そうでない場合でも有効だと思う．そして最後は問題集などの答えでよく書かれている式で，よく質問されるポイント．「2次方程式の重解」が問題になったときはいつでも使えるようにしよう！

2次方程式の重解について

今回は2次方程式が重解をもつ条件とその解について書きます．すべてを携帯用で書くのはきついので，今回は問題だけは携帯でも見れるようにしておきます．[問題]～携帯用～2次方程式2x^2-3kx+18=0が重解をもつようにkの値を定めよ．また，そのときの重解を求めよ．とりあえず問題だけアップ．解答・解説はまた後で．

第5弾・第6弾をまとめて解く方法

今回は相加・相乗平均の関係に関する問題の第5弾・第6弾をまとめて解く方法について書きます．[問題]～携帯用～x/(x^2+x+1)の最大値と最小値を求めよ．考え方としては，分母も分子も好き勝手に動かれては，全体の動きなんてさっぱり分からない．ということで，全体を一つの文字においてしまえば動きがみやすくなります．つまり，与式を k とおいて，k の最大値・最小値を求めようということです．[解答]～携帯用～x/(x^2+x+1)=k とおくと，kx^2+(k-1)x+k=0 ・・・(1)となる．x は実数であるから，(1)が実数解をもつ条件を求める．(i) k=0 のとき(1) ⇔ -x=0 ∴x=0(ii) k≠0 のとき(1) の判別式を D とすると，D=(k-1)^2-4k^2=-3k^2-2k+1(1) は実数解をもつから，D≧0 より，-3k^2-2k+1≧0⇔ 3k^2+2k-1≧0⇔ (3k-1)(k+1)≧0∴ -1≦k≦1/3，k≠0(i)，(ii)より，-1≦k≦1/3k=-1 のとき，x=-(k-1)/(2k)=-1k=1/3 のとき，x=-(k-1)(2k)=1であるから，求める最大値・最小値は次のようになる．最大値 1/3 (x=1 のとき)，最小値 -1 (x=-1 のとき)

第6弾～変数変換の重要性と定義域の変化～

相加・相乗平均の関係に関する問題の第6弾．今回は「変数変換の重要性と定義域の変化」について書きます．[問題]～携帯用～x＜0のとき，x/(x^2+x+1)の最小値とそのときのxの値を求めよ．前回と同じ問題ではないですよ．分数式における最小値を求める問題．ということは「相加・相乗平均の関係」を使うだろうと予測．しかし，今までの問題とは大きく異なる点がある．x＜0という条件に要注意．これでは「相加・相乗平均の関係」が使えない．じゃあどうするか？「負」だから使えない．なら「正」にしてしまえばよい．というか，「負」って考えにくい！「正」の方が考えやすくない？ってことで無理やり正にしてしまいましょう！そして，これが今回の最大のポイント！「x＜0のときは，t を正の数として，x＝-t と置き換えて考える！」何回も言ってると思うけど，これは思いついているのではない．こうすれば考えやすいから・解けるからこうするのだ．こういう一つ一つの考え方を理解し，覚えていくことが重要だ．「答え」を理解・暗記するのではなく，「考え方」を理解・暗記するのだ．見たことのない問題を解く際には，まず自分が解いた問題の中で「似たような問題」を探す．脳内検索によって類似問題が見つかった場合，その問題で使った解法を当てはめてみる．それで解ければ問題なし．解けなければ，また脳内検索をして次の手を考える．それでも解けない場合，その問題を解くための「知識」がないか，「道具の使い方」が分からない（気付いてない）かどちらかだろう．どちらの場合でもその問題を解くための「知識」や「道具の使い方」を吸収して忘れないようにすればよい．それでは実際に変数変換してみよう．[改題]～携帯用～t＞0のとき，-t/(t^2-t+1)の最小値とそのときのtの値を求めよ．これで解けるかな？前回と同様，分数式の変形における原則が満たされているので，分母・分子を同じ式で割ることを考える．つまり，分母・分子を t で割れば解決！改題の解答は，元の問題の解答とほとんど重複するため，元の問題の解答を書きます．[解答]～携帯用～tを正の数として，x=-t とおくと，（与式）=-t/(t^2-t+1)となる．分母・分子をt(≠0)で割って（与式）=-1/(t+1/t-1)t＞0だから，相加・相乗平均の関係より，t+1/t≧2√(t・1/t)=2⇔ t+1/t-1≧1⇔ 1/(t+1/t-1)≦1∴ -1/(t+1/t-1)≧-1（等号成立は，t＝1 ⇔ x=-1 のとき）したがって，求める最小値は-1（x＝-1 のとき）

第5弾～相加相乗平均の関係と最大値～

相加・相乗平均の関係に関する問題の第5弾．今回は「分数式の変形におけるもう一つのポイント」について書きます．[問題]～携帯用～x＞0のとき，x/(x^2+x+1)の最大値とそのときのxの値を求めよ．この問題の分数式は「（分子の次数）＜（分母の次数）」を満たしているので，別の変形を考える．さてどうしよう？もう一度問題文を見てみよう．「最大値」を求めよ．ってある．今までは「積が一定」となるように変形して，「最小値」を求めてきた．ところがこの問題では「最大値」が知りたいらしい．じゃあ「逆数の最小値」を求めればよいってことになる．aが最大となるとき，aの逆数1/aが最小となるってことね．[改題]～携帯用～x＞0のとき，(x^2+x+1)/x の最小値とそのときのxの値を求めよ． こうなれば分数式の変形における原則「（分子の次数）＜（分母の次数）となるように変形する」に従って変形することができる．[改題の解答]～携帯用～（与式）=x+1/x+1x＞0だから，相加・相乗平均の関係より，x+1/x≧2√(x・1/x)=2∴ x+1/x+1≧3 （等号成立は x＝1 のとき）したがって，求める最小値は3 （x＝1のとき）「逆数をとって問題を変える」ことをせずに解答を書いてみよう．そこで分数式の変形において，もう一つのポイントがある．「分母・分子を同じ数(式)で割る」ということだ．つまり，この問題では分母・分子を x で割ることによって，改題と同じ操作を行うことができる．まぁ同じことなんですけどね・・・利点は「逆数の最小値を求めればよい」と書かずに済むくらいですね．[解答]～携帯用～分母・分子をx(≠0)で割って（与式）=1/(x+1/x+1)x＞0だから，相加・相乗平均の関係より，x+1/x≧2√(x・1/x)=2∴ x+1/x+1≧3∴ 1/(x+1/x+1)≦1/3（等号成立は，x＝1 のとき）したがって，求める最大値は1/3（x＝1のとき）

第4弾～分数式の変形における原則～

相加・相乗平均の関係に関する問題の第4弾．今回は「分数式の変形における原則」について書きます．では問題です．[問題]～携帯用～(x^4+7x^2+19)/(x^2+2) の最小値とそのときの x の値を求めよ．ここで，「a^b」は「a の b 乗」を表すことにします．またまた分数式の最小値を求める問題．しかし，今までとは異なり，積が一定というのが見えない．何とか積が一定になるように変形しなければならない．どのように変形するか？その変形方法がポイントである．分数式の変形における原則というものがある．それは「（分子の次数）＜（分母の次数）となるように変形すること」である．これは具体的には「割り算」をすることによって可能である．[重要事項]～携帯用～整式 A を整式 B で割ったときの商を Q，余りを R とすると，A=BQ+R　← 7=2×3+1 という感じと表すことができる．両辺を B で割るとA/B=Q+R/B ← 7/2=3+1/2 という感じとなる．この問題の場合，(x^4+7x^2+19)÷(x^2+2)をすることによって，分子の次数を分母の次数より低くすることができる．割り算の結果，x^4+7x^2+19=(x^2+2)(x^2+5)+9 となるから，(x^4+7x^2+19)/(x^2+2)=x^2+5+9/(x^2+2)と変形できる．ここから前回同様，積が一定になるようにするにはどうすればいいか？を考えると，(x^4+7x^2+19)/(x^2+2)=(x^2+2)+3+9/(x^2+2)となる．この後は相加・相乗平均の関係が使える条件に気を付けるだけです．[解答]～携帯用～(x^4+7x^2+19)/(x^2+2)=(x^2+2)+9/(x^2+2)+3x^2+2>0 だから，相加・相乗平均の関係より，(x^2+2)+9/(x^2+2)≧2√{(x^2+2)・9/(x^2+2)}=6∴ (x^2+2)+9/(x^2+2)+3≧9（等号成立は，x^2+2=9/(x^2+2)，すなわち x=±1 のとき）したがって，求める最小値は9（x=±1のとき）

第3弾～式変形における工夫～

相加・相乗平均の関係に関する問題の第3弾．今回は「相加・相乗平均の関係を使える形に式を変形する」ことについて書きます．では問題です．[問題]～携帯用～x>-1のとき，x+3/(x+1)の最小値を求めよ．分数式の最小値を求める問題．ということでほぼ「相加・相乗平均の関係」を使うだろうと予想．初めから「相加・相乗平均の関係を使う問題」とは見ていないということを前提としているのでこういう書き方になります．「相加・相乗平均の関係」を使って，最小値を求めるには，公式の形から考えると「積が定数」になるようにしなければならない．分母が x+1 であるから，積が定数になるためには，x+1 が分子にもなければならない．ここで分母を x にすることも考えることも出来るが，分数の分母を変えるなんて難しすぎるので分子で「調整する」ということです．x+3/(x+1)=x+1+3/(x+1)-1 と変形しよう．x を x+1-1 と変形していることがポイント．この変形はよく使うので覚えておこう．それでは解答です．[解答]～携帯用～x>-1 より，x+1>0 だから，相加・相乗平均の関係より，　x+1+3/(x+1)≧2√{(x+1)・3/(x+1)}＝2√3　∴ x+3/(x+1)≧2√3-1（等号成立は，x+1=3/(x+1) すなわち x＝√3-1 のとき）したがって，求める最小値は 2√3-1（x＝√3-1 のとき）

第2弾の解説

現在福井校舎で TeX が使えないが、書けそうなので解説を書いてみよう。実際には TeX の図の方が見栄えは良いが、携帯からは見れないという欠点もある。見栄えを気にしなければ、TeX を使わずに書いたほうが良いのだろう。それでは解説です。二つの答案のうち、答案 I が間違っています。ではどこが間違っているのか？ポイントは「その等号は本当に成り立つの？」である。まずは、次の事項は分かるだろうか？A≧B＞0，C≧D＞0 のとき，AC≧BD が成り立つ．（等号成立は，A＝B かつ C＝D のとき）証明は次の通り。A≧B＞0 の辺々にC(＞0)を掛けると，　　　AC≧BC（等号成立は，A=B のとき）・・・(1)となる．　また，C≧D＞0 の辺々にB(＞0)を掛けると，　　　BC≧BD（等号成立は，C=D のとき）・・・(2)となる．　(1),(2)より，AB≧BC≧BD が成り立つ．　したがって，AC≧BD となる．等号成立は，A=B かつ C=D のとき．答案 I の等号が成立する条件について考えてみよう！1 の等号成立条件は、a=2/b ⇔ ab=2 のとき。2 の等号成立条件は、b=3/b ⇔ ab=3 のとき。1,2 をまとめた最後の式における等号成立条件は、ab=2 かつ ab=3 のときである。これを満たす a, b は存在しない。つまり、1,2 をまとめた最後の式の等号は a, b をどのような値にしたとしても成り立つことはない。では、次に答案 II について考えてみよう。答案 II における等号成立条件は、ab=6/ab のとき。すなわち、ab=√6 のときである。ということで、ab=√6 のとき、与式は最小値 5+2√6 をとる。今回の例からも分かるように、常に「等号が成立するかどうか」を考えることが大切である。したがって、「～の最小値を求めよ」という問題文のあとに「また、そのときの～の値を求めよ」となくても、最小値をとるときの変数の値を考えるようにしたほうが良い。

第2弾～よくある誤答例～

この問題に対して，次の二つの答案があります．この二つの答案のうち，どちらか一方が間違っています．どちらが間違っているのか？どこが間違っているのか？

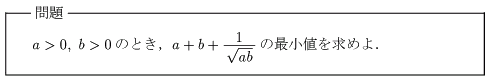
第1弾～相加・相乗平均の関係～

「相加・相乗平均の関係」は最大・最小問題によく使われる．数3の微分を学習する前に，分数式の最大・最小問題が出題されれば，必ずと言っていいほど「相加・相乗平均の関係」を使う．では次の問題を考えてみよう．最小値の求め方には「グラフを描く」という視覚化する方法もあるが，2変数では無理．さらに，分数で表されているから数3の微分を知らないとグラフさえ描けない．こうなれば間違いなく「相加・相乗平均の関係」を使う．ここで，最小値の捉え方を変えてもらいたい．「y の最小値を求めよ」と言われれば，「y≧m」という不等式を導けばよい．そうすることによって，m が y の最小値ということになる．最大値と言われれば，不等号の向きが逆になるだけ．最小値を不等式と関連付ければ，「相加・相乗平均の関係」とも結びつきやすくなる．今回の問題の場合，一発でその不等式を導くのは困難．ということで，次がポイントとなる．A≧B かつ B≧C のとき，A≧C．等号成立は，A=B=C のとき．こんなの当たり前と思うだろうが，結構重要．A と C をつなぐためのワンクッションが非常に重要．不等式の証明などではこの考え方をかなり使う．ということで解答は次のようになる．

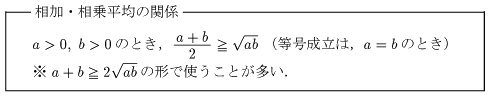
相加・相乗平均の関係

不等式の証明や最大・最小問題に用いられて，使いどころが良く分からないとされている「相加・相乗平均の関係」について．証明に入る前にちょっと余談．相加平均とは，ごく普通の平均のこと．a と b の相加平均とは，同じ2数を足して a+b になるものだから，(a+b)/2 となる．相乗平均とは，掛け算の平均のこと．は？何のこっちゃ？ってなるけど，分かれば簡単．a と b の相乗平均とは，同じ2数を掛けて ab になるものだから，ab の平方根．つまり，√ab となる．ってことで証明いってみよう！

第5弾の証明

この問題は等式の証明に必要な考え方を知らないと解けない．当然であるが，何を証明すればよいのかが分からないと証明なんてできるわけがない．この場合は，「x, y, z のうち少なくとも1つが1に等しいこと」を証明すればよいのだが，それは問題文を見れば分かることであって，僕が言いたいこととは違う．条件として式が与えられていて，示すものが式で書かれているならまだ楽である．しかし，今回は条件として式が与えられていて，示すものが言葉で書かれている．この場合は条件式を言葉で表して，「言葉→言葉」の論証で攻めるか，示すものを式で表して，「式→式」で攻めるかどちらかである．論証より「式→式」の方が楽だと思う．つまり「x, y, z のうち少なくとも1つが1に等しい」ことを数式で表すことを考えなければならない．「3つのうち少なくとも1つは1」ということは，最低でも1つは1ということ．つまり，1つが1でもいいし，2つが1でもいいし，3つとも1でもいいということ．x, y, z のうち少なくとも1つが1に等しい ⇔ x = 1 または y = 1 または z = 1となる．しかし，これではまだダメだ．「または」っていう言葉が入ってるからね．このままでは難しいので次の問題を考えてみよう．この逆はよく使っていると思う．2次方程式を解く際に絶対使っている事項だ．a, b のうち少なくとも一つは 0 ということは，a = 0 または b = 0 ということ．つまり，積が 0 ということ．次にこれを発展させていく．a, b の少なくとも一方が 1 に等しい⇔ a = 1 または b = 1⇔ a - 1 = 0 または b - 1 = 0ここまで来れば分かりますね．a, b の少なくとも一方が1に等しい ⇔ (a-1)(b-1)=0元の問題に戻ります．x, y, z のうち少なくとも1つが1に等しい⇔ x=1 または y=1 または z=1⇔ (x-1)(y-1)(z-1)=0ということですね．これで示すべき等式が得られました．あとは書く量を減らすために，「文字の置き換え」という工夫をします．具体的には，x-1, y-1 z-1 をそれぞれ他の文字，例えば a, b, c とおきます．x+y+z=3 は a+b+c=0 と書き換えることができます．この結果，次のように問題を単純化できます．こうなればかなり簡単ですね．前にも書いた公式 を利用することは見え見え．ってことで証明は次のようになります．

等式の証明 第5弾

次の問題を考えてみてください．

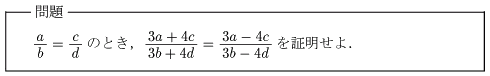
比例式

等式の証明の第4弾！今回は「比例式」について．比例式って何？っていう人の為に．この問題で与えられている条件式のことを比例式って言います．つまり，「比の値」が等しいことを示す式のこと．比例式は k とおくのが鉄則！ということで証明です．

因数分解公式の導出～3次式～

さっきの記事で使った因数分解公式の導出をします．

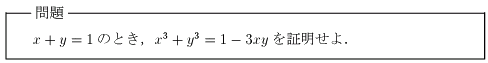
どうせ書くなら格好良く♪～等式の証明～

それでは等式の証明の具体例第3弾．条件式が1次式だから，原則の一文字消去．x と y についてはどちらも次数が同じなので，どちらを消去しても構わない．しかし，y の式より x の式の方が見慣れているため，y を消去して x の式にする．あとは x の方が y に比べて書く時間が短くて済む．スピードは重要ですよ～！次は式を見て左辺はすぐに「対称式」と分かるので，基本変形を元にした証明．次は前の記事で書いた「0」に着目する証明方法．ここで，因数分解が難しいと思うかもしれないが，実は因数分解公式そのまんま．この公式において，a=x, b=y, c=-1 とすればよいが，そんなの気付かないと言われそうなのでもう一度言います．x+y-1=0 なんだから，（左辺）-（右辺）=(x+y-1)×□ となるはず．で，3次式の因数分解で片方が3項式ということは上記の公式でいけるんじゃないの？という感じです．ただ，実際にはこの問題では，証明2を選びますね＾＾；だって書く量少ないし，格好良いからね♪

2文字の対称式

次の具体例を出す前に必要な事項を一つ．「対称式」について．x,y の対称式とは，x と y を入れ替えても元の式と同じ式になる式のこと．その中で最も簡単な x+y, xy を基本対称式という．x+y において，x と y を入れ替えると y+x となりこれは元の式と同じ．xy において，x と y を入れ替えると yx となりこれも元の式と同じ．そして，次が対称式の最大のポイント．全ての対称式は基本対称式のみで表すことが可能．つまり，2文字の場合，次のように表すことができる．(4),(5)については x+y, xy で表されていないが，(1),(2)を用いればよいので通常はここで変形を止める．

等式の証明～条件つき～

条件がある場合の等式の証明の具体例．条件式が1次式であれば，原則は一文字消去．文字数が少ないほど，式はより簡単になります．だから一文字消去することによって，式を簡単にして証明しやすくするということ．この場合，a=-b-c, b=-c-a, c=-a-b の3通りから選ぶことができます．どれにするか？どれでもいいということはなく，見るべきところがあります．各文字の次数に着目しないといけない．最も次数が低い文字を消去するべきですね．なぜか？a=-b-cを代入してaを消去するとなると，2乗の展開をしないといけない．2乗くらいなら良いのかもしれないが，5乗ならどうだろう？好きな人はいないと思う．ってことで最低次数の文字であるcを消去ってことです．一文字消去の場合，証明方法は両辺ともに同じ式に変形する(ii)の方法を選ぶことになります．次にテクニカルな証明の紹介．大抵の問題集には別解として書かれている方法です．しかし，何故そのような証明ができたのか？ということにはほとんど触れられていません．この証明方法は決して思いつきや行き当たりばったりでたまたま成功したわけではありません．証明できる理由があります．ということでその部分を説明します．ここからは超重要部分！ってことで口調を変えて説明する！今しようとしていることは「等式の証明」．つまり，左辺と右辺が等しいことの理由を述べなければならない．証明方法(iii)を選べば，（左辺）-（右辺）=0 になる理由を述べなければならない．ここで，条件なるものが存在し，それが a+b+c=0 となっている．「0」っていう数字に着目だ！この条件がなければ，（左辺）-（右辺）が0になる理由はなくなる．この条件があるからこそ，（左辺）-（右辺）=0 となる．つまり，（左辺）-（右辺）=(a+b+c)×□ とならなければならない！これ以外の形では，絶対に（左辺）-（右辺）=0 とはならない．したがって，（左辺）-（右辺）を因数分解すれば必ず a+b+c が出てくるという自信を持って計算していけばよい．決して思いつきやひらめきで証明2があるわけではない．ただ，この1問だけだと，やっぱたまたまじゃないの？って思われるので違う例も紹介していきます．お楽しみに♪

等式の証明～条件がない場合～

とりあえず具体例一発目．前の記事で書いた「簡単な式」「複雑な式」とはどういう式なのか？ここで言う「簡単な式」とは「手を動かさなくても容易に展開できるような因数分解された式」や「非常に単純な単項式(この表現は許して欲しい)の和や差で表された式」のこと．「複雑な式」とは「累乗(2乗とか3乗のこと)の和や差で表された式」で展開するのも嫌になるような式のこと．この問題で言えば，左辺が簡単な式(ここはあえて突っ込まないで下さいm(_ _)m)で，右辺が複雑な式ということになる．基本に従えば，(i)の方法ですることになる．つまり，複雑な式である右辺を因数分解することによって左辺を導くという方針．等式の証明で行う因数分解はこうなるという「答え」が見えているから，自分で考えなくても良いという意味で「簡単」ですね♪そんなわざわざ因数分解しなくてもいいんでは？ってなるのは分かります．でも「因数分解されている式に向かって変形していく力」は絶対必要だと思います．あとは実際に分かっていなくても，所々省略して正しい証明として見せることができます(笑)ってこんなこと書いたらまずいかもしれませんが，「見せる解答」もテクニックの一つですからね．ただ，これくらいの等式であれば展開してしまった方が速いです・・・だから大抵は次の証明IIでするでしょう＾＾；

訂正

先ほどの記事で，等式の証明方法は3通りしかないと書きましたが，実はもう一つあります．僕の中で，勝手に範囲を「数2」としていました．「数B」を範囲に含めると「数学的帰納法」という方法もあります．まだ忘れている方法があるかもしれません．お気づきの方はコメントかメールして下さいm(_ _)mとりあえずは数2で扱う等式の証明について書きます．

等式の証明方法

等式の証明方法について書きます．ある等式を証明せよと言われれば，上記の3通りしか方法はありません．(i)の方法は，左辺を変形して右辺を導く方法．当然であるが，右辺を変形して左辺を導いてもよい．等号なんて「左辺と右辺が等しい」という意味しかないからね．一般的には，片方が複雑な式で，もう一方が簡単な式のときに使う方法である．複雑な式をもう一方の式を見据えて簡単な式に変形していくと証明が完了する．(ii)の方法は，両辺をそれぞれ変形して同じ式を導く方法．一般的には，両辺とも複雑な式で，(i)の方法では難しい場合に使う方法である．両辺ともにできるだけ簡単な式に変形すると証明が完了する．(iii)の方法は，両辺が同じ式って言ってるんだから引けばなくなって0になるだろっていう方法．条件が付いていない等式の証明では(i)か(ii)の方法で解決できるため，一般的には，条件が付いている場合の証明に用いる方法である．テクニカルな証明をしたいときに良く使われる．

条件付き最大値問題

E'z先生の記事で扱われた問題．まずは一般的な解法から．範囲は数I．なぜx+2yをkをおくのか？「xとyがバラバラに動いて困るから」ですね．2文字が動くより，1文字が動いた方が考えやすいでしょ？これによりx+2y=kと一次方程式の形になるから，することと言えば一文字消去．ということで与えられた条件がyに関する二次方程式になります．ここで問題文の「実数」というのがポイントとなってきます．「ある実数が2次方程式を満たしている」 ⇔ 「判別式が0以上」これで解けますね．次は数IIで円と直線を使った解法．解Iと同じようにx+2y=kとおきますが，捉え方が異なります．一次方程式の形だから直線と捉えることができます．さらに，与えられた条件は円と捉えることができます．両方同時に満たさないといけないから，直線と円が交わらないといけない．ということで直線が円と共有点をもつ条件を考えれば解けますね．解IIIは解IIと同じように与えられた条件を円として捉えますけど，パラメータ表示にもちこみます．x=cosθ，y=sinθとおいたあとは三角関数の最大値問題に帰着できる．あとは「三角関数の合成」を使えば解けますね．範囲は数II．解IVは是非使えるようになって欲しい解法．範囲は数B．

放物線と接線と面積

1998年一橋大学の第4問でも出題されている有名問題．この問題に関して，導出方法・結果をしっかり覚えておこう．

放物線と直線で囲まれる図形の面積

前の記事を発展させるために必要な問題．ここで，上記の積分計算では次の公式を使っています．その証明です．厳密には数3の積分計算を使ってますが，数2までの生徒も覚えておくべきでしょう．結局xの2乗の係数と2交点のx座標だけが分かれば，放物線と直線で囲まれた図形の面積は次のようにして求めることができる．

放物線の接線の交点

放物線の接線に関する問題でいろいろなところで見る問題．「交点Rのx座標が2点P,Qの中点のx座標と等しい」ことを覚えておこう．

放物線上の点における接線

放物線について，変化の割合，直線の方程式，三角形の面積(証明)と扱ってきました．今回のテーマは接線．まずは一般的な解答から．以前書いた「2点を通る直線の方程式」を用いて点Pにおける接線を求めます．これを使うと「放物線上の2点を通る直線」でも「放物線上の点における接線」でも同じように求めることができます．

センター試験の感想

IAは正直，平均点が下がった理由が分からない．第2問の最後と第3問でつまづいた人が多数いる？IIBもそれほど難しいわけではないが，とにかく計算が鬱陶しい．計算スペースがなければ辛いかも？結果として難しくなったという感じか・・・(IAについて)第1問[1]は去年と同じ．特に言うことなし．[2]は「コ」に少し戸惑う？第2問(1)の頂点の座標，x軸と2点で交わる条件は定番問題．(2)の最大最小問題は得意技が使えないように工夫されていたが，問題ではない．最小値が6のときの最大値Mの求め方によっては差が出るか．第3問(1)の角度は図を描けば瞬解．半径は正弦定理で終わり．(2)の設定に少し戸惑うかもしれないが，面積による設定は2002年センター試験に出ている．ソ～ツに梃子摺った人がいるかも？第4問何度もやっているだろう問題．(IIBについて)第1問[1]はわざわざaとbにおいてるのがミスを誘う．[2]は対数関数の基本が出来ていれば大丈夫．第2問初めのg(x)-f(x)で間違えると全滅を喰らう恐ろしい設定．(3)の面積は公式が使える．最後のtanθは微分係数と加法定理でさっくり出そう．第3問(1)はいきなり漸化式だけど最も簡単なパターン．Sn>0を満たす最小のnは適当に値を代入して確認．(2)は久々にこのタイプを見たという感じ．一度経験してないと苦しいか？(3)は(2)が分からないとお手上げ状態．逆に(2)が出来ていれば，ひたすら計算するのみ．そういう点ではバランスは取れている？第4問ひたすら面倒な計算が続くだけ．計算スペースがあるのか？

整数問題～考え方～

今回は前の記事で扱った整数問題の解答に至るまでの考え方について書きます．どうやって考えたか思い出しながら書きます．q, 2q+1, 4q-1, 6q-1, 8q+1 がすべて素数という条件から，まず分かることは何か？「q」がある以上，qが2以外の偶数のときは不適だと分かります．というかq自体が素数でないといけない．それを踏まえて，とりあえず「実験」です．q=2のときは順に，2, 5, 7, 11, 17となりすべて素数であるから解．q=3のときは順に，3, 7, 11, 17, 25となり「25」が素数でないから不適．q=4は偶数だから飛ばす．q=5のときは順に，5, 11, 19, 29, 41となりすべて素数であるから解．q=6は偶数だから飛ばす．q=7のときは順に，7, 15, 27, 41, 57となり「15, 27, 57」が素数でないから不適．q=8,9,10は素数でないから飛ばす．q=11のときは順に，11, 23, 43, 65, 89となり「65」が素数でないから不適．これ以上は数が大きくなるから調べる時間が無駄．q=2, 5 が解？でも他にあるかもしれない．第一，問題が「すべて求めよ」ということから場合分けが絶対必要．問題はどのようにして分けるか？qは奇数と決まっている以上，偶数，奇数の2つの場合分けは出来ない．ではどうするか？あまり場合分けが多くても嫌だから，次に少ない3つの場合分けで済む3の倍数で分けてみる．(I)q=3n(n≧2)のときqが3の倍数となるから，明らかに不適．(II)q=3n+1(n≧1)のときとりあえず2q+1から順にどうなるか計算．2q+1=2(3n+1)+1=6n+3=3(2n+1)初めに調べた2q+1がたまたま3の倍数となり不適．結構調子良く進む．このまま終わったら楽だなと思いながら次へ・・・(III)q=3n+2(n≧1)のときこれも2q+1から順にどうなるか計算．2q+1=2(3n+2)+1=6n+54q-1=4(3n+2)-1=12n+76q-1=6(3n+2)-1=18n+118q+1=8(3n+2)+1=24n+17なんだこれ・・・うまく行かない．他の場合分けって言っても，q=3n+2のときだけが問題だからこのまま行きたい．ってことで，nを偶数・奇数の2通りに分けてみることに・・・(i)n=2m(m≧1)のときq=3×2m+2=6m+2=2(3m+1)となり偶数となるから不適．あとはnが奇数のときのみ！(ii)n=2m+1(m≧1)のときq=3(2m+1)+2=6m+52q+1=2(6m+5)+1=12m+114q-1=4(6m+5)-1=24m+196q-1=6(6m+5)-1=36m+298q+1=8(6m+5)+1=48m+41あらま・・・うまく行かない・・・ここから更に場合分けは答案が汚くなりすぎて嫌．でもq=2,5以外に解があるとは考えにくい．ってことはどれかが必ず何かの倍数になるはず．ということでここでまた実験．とは言え，そのままの数字を書くと大変．倍数で見分けやすいのは何か？5の倍数なら一の位が0か5になるからすぐ分かる．しかもq=11(=3×3+2)のときに5の倍数が実際に存在することから，どれかが必ず5の倍数になるのではないか？と予想．とにかく実験．一の位のみ考える．　　　　q=6m+5・・・1, 7, 3, 9, 5, 1, ・・・2q+1=12m+11・・・3, 5, 7, 9, 1, 3, ・・・4q-1=24m+19・・・3, 7, 1, 5, 9, 3, ・・・6q-1=36m+29・・・5, 1, 7, 3, 9, 5, ・・・8q+1=48m+41・・・9, 7, 5, 3, 1, 9, ・・・一の位に注目すると，必ずどれかが5になっている．これで解はやはりq=2, 5以外にないことが分かるけど，解答としては汚くて仕方がない．もう一度一の位に注目．すべてが周期5になっていることが分かる．周期が5・・・ってことは初めから5の倍数で分ければいいんじゃないの？ということで5の倍数で分けました．

整数問題

三角形の面積-証明

先ほどの記事の公式の証明です．ベクトルを用いて求めます．途中のベクトルを用いた面積公式の導出は，入試問題にもなっていますね．中学生にはこの解説はできないので，結果のみ教えてます．

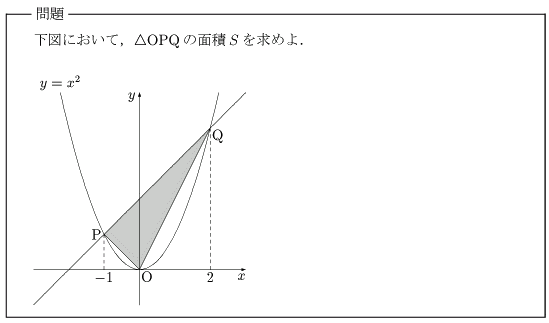
三角形の面積

変化の割合，直線の方程式と続いて今回扱うのは「三角形の面積」です．では問題．通常ならy軸で二つの三角形に分割して面積を計算します．その際にはy切片が必要．前の記事で扱った「直線の方程式」からy切片は一瞬で求まりますね．具体的には，-1×(-1)×2＝2となるので，底辺を2として計算すれば良いですね．今回は便利な面積公式を紹介します．この公式を使うときの注意点は「3点のうち必ず1点は原点でなければならない」ということです．もし一つも原点でない場合は，一つが原点に来るように平行移動してしまいましょう．この公式を使うと，次のように面積を計算することができます．

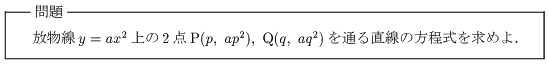
放物線上の2点を通る直線

昨日書いた「変化の割合」を発展させます．直線の方程式を求めるときに必要になるものは何か？「傾き」と「通過する1点」である．つまり次の公式を活用する．この問題の場合，傾きは前の記事で書いたことを覚えていれば一瞬で出る．通過する1点は点Pか点Qを使えばよい．したがって，解答は次のようになる．ここで重要なのは，この直線の方程式を公式として覚えてしまうことだと思う．

中学数学～変化の割合～

今回は中学生向けの記事ですが，高校生で知らない人はしっかり理解して使えるようにして下さい．今回は文字の大きさを少し大きくし，枠で囲んでみました．ではいきます．簡単に解ける問題ですが，3秒で出来ますか？まずは普通の解答から．この方法だとyの値を求めないといけないので3秒で解くのは無理だし面倒．yの値を求めないと変化の割合が出ないのかというとそんなことはない．ということで次の公式を覚えましょう．この公式を知っているのと知らないのでは全然解く時間が違ってきます．記述式なら最初の解答のように書いた方がいいですが，答えのみでも良い場合は次の別解のようにしてさっさと求めてしまいましょう！

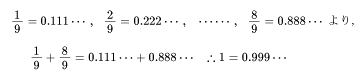
0.999・・・=1

マキバオー先生の記事でも扱われてますが，別解を示しておきます．まずは小中学生向き解答です．と言ってもマキバオー先生が中学生のときに聞いたもの(あの解法は僕も聞きました)の足し算版です．続いて数3で学習する「無限級数」に関する証明を示します．