2008年10月の記事
全17件 (17件中 1-17件目)
1
-
3日間合宿
忙しくなりそうw帰ってくるまでしばらく日記書けません。せっかくの3連休なのになぁ。まあ、ネタ探しも込めてちょっと行ってきますね!
2008.10.31
コメント(1)
-
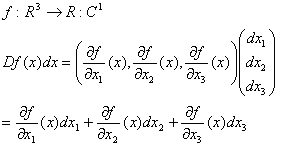
線形近似と変数変換による体積比の図式化
微分によって得られた導値で、局所的に線形近似をする様子を図式化してみた。ちなみに値域が3次元ユークリッド空間の場合には図式化はここまで上手くいかない。実際、fの値域は1次元ユークリッド空間であるが、三次元的に近似を表現している。続いて、変数変換で重要になるヤコビ行列による体積変化について。ここでは次元が下がらないように、ヤコビ行列式は0にならないと仮定する。微少体積dx・dy・dzが関数によって図のような3つのベクトルの張る平行六面体に写される。と言っても、これは局所的に見ればの話で、大域的には平行六面体にならない。ただ、gが線形写像の場合は、どんな体積の大きい図形に対しても、完全な平行六面体となる。また時間があれば、今度はヤコビ行列が0とならない点で局所的に逆行列が存在することを図式化したいと思う。
2008.10.30
コメント(0)
-
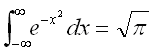
へこみますw
私がセミナーで使っている教科書からの引用。《普通の人にとって2掛ける2が4であることがあたりまえであると同じくらいにこの等式があたりまえに見える人こそ数学者と呼ぶに値する。リウヴィルは数学者であった》 -ケルヴィン卿(ベクトル解析より)う~ん、当たり前では無いと思うんだが。
2008.10.28
コメント(3)
-
曲線(解答)
原点中心に回転していますから、まずは極座標表示を使います。Arctantは、実数全体から(-π/2,π/2)への関数です。なのでまず、1/π倍して、値域の動く範囲を幅1にします。1/π*Arctantこれで値域は(-1/2,1/2)ですね。続いて、上に3/2平行移動しましょう。1/π*Arctant+3/2値域は(1,2)になりました。これが半径1の円と半径2の円に巻きつく曲線を作るポイントです。最後に、x,y軸に射影します。x=(1/π*Arctant+3/2)costy=(1/π*Arctant+3/2)sintこの媒介変数表示が答えになります。他にも有界な範囲に値域を持つ関数なら、できるんじゃないでしょうか。
2008.10.25
コメント(0)
-

曲線
今日、学校の授業で出てきた変わった曲線。どうやって描いたかわかりますか?ヒントはタンジェントの逆関数です。
2008.10.23
コメント(4)
-
被害妄想
今日、夜にマックに行ったとき、たまたま線形代数の双対空間の性質を頭の中で考えながら店員と応対していたのだが、その時の会話。店員「店内でお召し上がりですか」私「ああ~、どうしましょうかねぇ」・・・。私「Take offで!!」店員「テイクアウトですか(; ̄Д ̄)!?」私「そうです」店員「料金880円になります」私「あれ?高くないですか?だってバーガーとポテトだけですよ?」店員「ああ、失礼しました。会計560円です」多分、私が上手く伝えなかったから料金が880円になったんでしょうが、そんなことはまあどうでもいいとして。問題は、私がTake offしてしまったことだorz直訳して離陸。旅立つ気でしょうか?もう英語を中高生に教える自信がないですwきっと厨房の裏でクスクス笑ってるに違いねぇ。
2008.10.18
コメント(4)
-
PS
友達からPSのソフトを借りました。PS3でやりました。スペックを異常に持て余しておりますw日本の歴代ゲーム機(ハード)を一気に解説してみた↑この動画、ちと長いのですが、こうして見てみると、少し前までは、ほんとに数多くのマニアックなハードが発売されていたわけです。最近では独占化が進んで任天堂、SCE、マイクロソフトくらいですが、当時は1年に1機のペースでゲーム機が発売されていました。こんなので50000円代かよ!!ってくらいのスペックのゲーム機もあります。それにくらべて今は大分ハードも進化して、これ以上のハード革新が見込めるのかなって思いますが、まあPS4とかは出るかもしれないですね。現状、俄然PCゲームのほうがスペックは上ですから。ゲーム機の未来予想図↑これみると、まあ確かに次世代って感じがしますけど。洗脳する気ですか?まあ今後に期待ですね。
2008.10.17
コメント(1)
-
ユークリッド空間と、一般位相空間における定義の比較
例えばR^nでは、closed set Aを、S:sub set,∀xk∈A,lim(k→infinity)xk=x⇒x∈Aで定義しますが、位相空間では、Acがopen setであることを定義とします。続いてclosureの定義Aa:=A∪{x∈R^n|∃xk st lim(k→infinity)xk=x,∀k∈N,xk≠x}で定義しますが、位相空間では、Aa:=intersection{F:closed set|F⊃A}で定義します。やはりどちらも前者のほうが幾何的でイメージがつかみやすいのではないかと思います。R^nだと通常の位相で、内点は集積点になる、これは開球体が連続濃度なので問題無いと思うのですが、一般の位相の場合は離散位相の場合、内点は集積点にはならないです。実際Aから一点集合{x}を除いたclosureはその集合と一致するからです。この場合は明らかにAの点、というかSの任意の点がAの集積点にはならないです。
2008.10.15
コメント(0)
-
数学教授名言集
私の所属する大学の数学の講義にて、その1 講義中に入ってきた事務員の事務的要請に対する反論「今、空間の次元を考えるのが必死でして…」 F先生その2 教授の大学2年時の体験「寝ているときに夢の中に位相空間の証明が出てきて、頭の中がグルグルになって…。起きたら汗でビッショリでした!」 N先生その3 講義中の失言「大体数学者は頭イッっちゃってますが、…」 F先生ウチの教授はマニアック揃いで面白いですね。
2008.10.15
コメント(0)
-
ポジティブシンキング
人見知り≒shy≒ツンデレこれはあると思います。ツンデレの認知度が上がれば、社会はもっとよくなると思います。
2008.10.13
コメント(3)
-
絶望先生
なんかDVD出るらしいです。2.5期とか書いてあります。公式HPもあるので詳しくはコチラ。人気アニメの続編がどんどん決定して本当に嬉しいですね~。みなみけ3期も期待ですね!ハルヒも早く出してくれないかな~、ゲームはもういいから。
2008.10.10
コメント(1)
-
今日の5の2を見た感想
先日、友人から勧められたので見ました。みなみけと同じ作者の作品らしいので期待していました。結果・・・。3人の女子生徒が俺の嫁になりました!・・・・・・・・・・・・・・・・・・。ということで今日の5の2は面白いです。にしても最近の小学生ってのはオシャレですね。かなりジェネレーションギャップを感じてしまうのですが、それは単に私が田舎育ちだからでしょうか?非常に独特の作風を持っていて、場の空気の演出がとても凝っていると思い、関心しました。最近、ゼロ魔とテレ蘭を挫折しかけている中で、これほど魅力的なアニメがあるとありがたい。
2008.10.07
コメント(0)
-
予想外
「あずきちゃん」という恋愛アニメが昔NHKでやってて、それの劇場版なるものが存在するらしくて、ニコ動で見てみました。あずきちゃんの弟、タママ二等兵!!これはおそらく昔聞いてたんだろうけど予想外でしたねwちなみにあずきは俺の嫁だが、俺はロリコンではない。古代の律令制の元では17~20歳を少女と定義してましたから。When in Rome,do as the Romans do(郷に入っては郷に従え)とは言うが、諺であるだけで別に根拠はないでしょう。開区間は必ずしもopen setにならないでしょう。密着位相だったらそうでしょう。
2008.10.06
コメント(1)
-
Life with PlayStation?
Folding@home?が一新されてLife with PlayStation?になったみたいですが、何か思いっきりGoogle earthっぽい。Wiiの地球儀とほとんど一緒みたいなもんです。唯一違うのはリアルタイムで画像が変化していることくらい。でもずっと見てるわけじゃないからそんなの気にしねぇ。あとタンパク質のシュミレーションは継続されるようですが、終了予定が翌朝の5時とか、どんだけ点けっぱなしにするんだよって話ですwとりあえず体験版で遊んでます。
2008.10.05
コメント(0)
-

勉強法
勉強のコツ、そう、こなたの下敷きである!!集中力250%UP、これは大きい。ただ大学では勇気が無いので使えないw
2008.10.03
コメント(1)
-

集合・位相入門
4つあった参考書のうち、あえて教授が”あまり一般にはオススメできない”と言ったものを注文してみた。集合・位相入門面白い。線形の100倍は面白い。
2008.10.01
コメント(0)
-
本末転倒
ネットで調べたら変換コネクタ3万以上。だったら安い液晶かったほうがええ。下宿するようになってから傘を5回くらい盗まれたのでそろそろ鍵をかけます。傘に鍵なんて俺も聴いたことは無いが、もうキレる一歩手前なので実施します。でも鍵の値段は傘の値段の3倍です。はぁうぅ~、高かったよぉ~w
2008.10.01
コメント(4)
全17件 (17件中 1-17件目)
1










