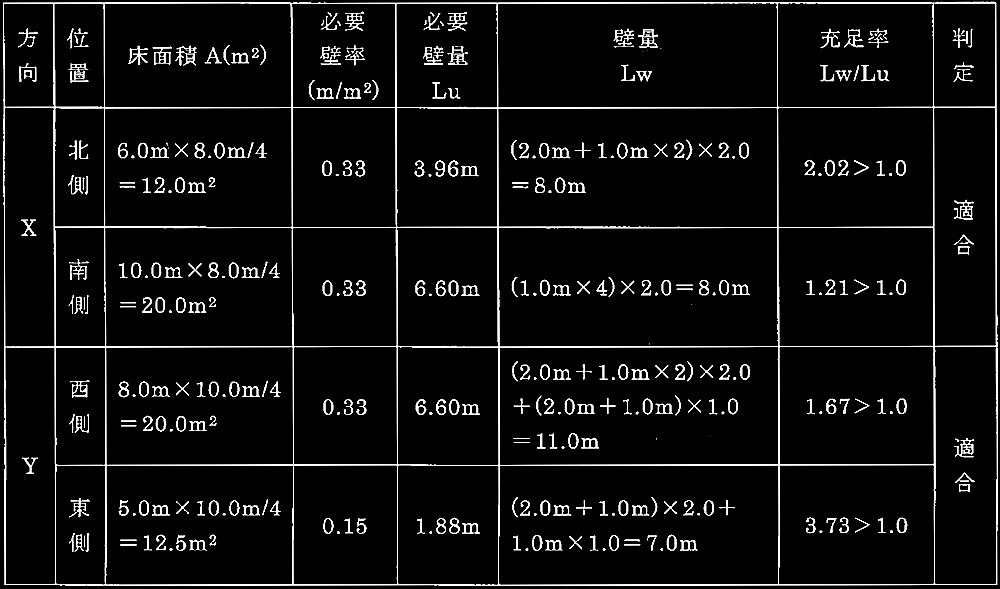
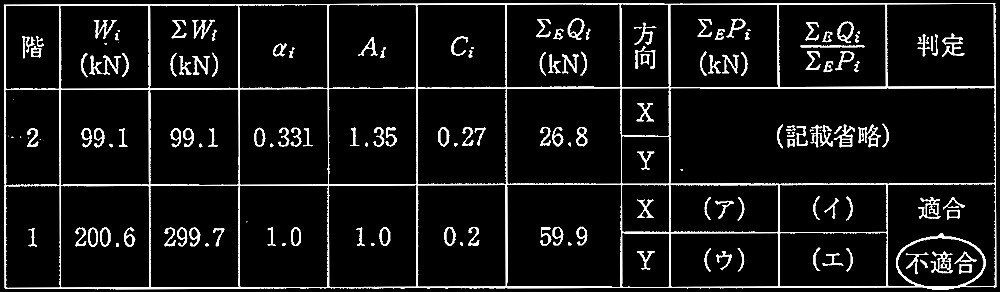
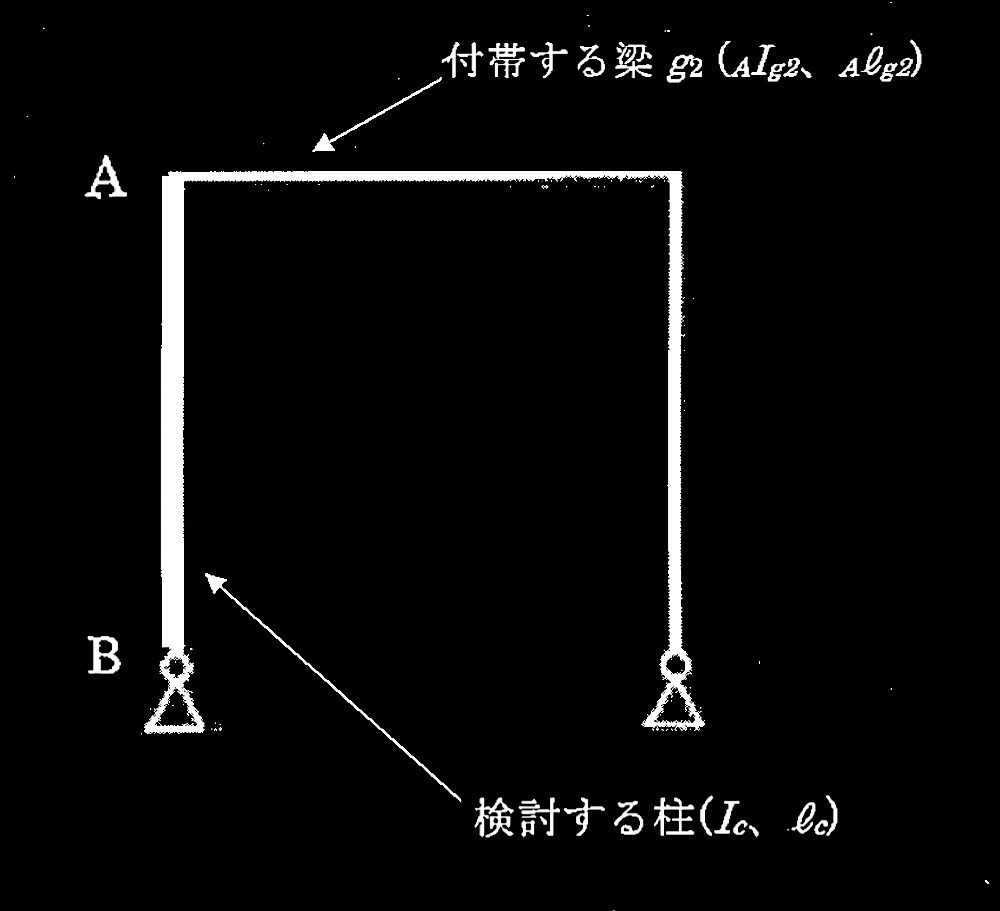
同一敷地内に鉄筋コンクリート造地下1階、地上8階建ての事務所棟と、鉄骨造地上3階建ての付属棟を計画する場合の基礎の設計に関する以下の設問に解答せよ。当該敷地の地盤調査の結果から想定される地盤概要を図1に示す。
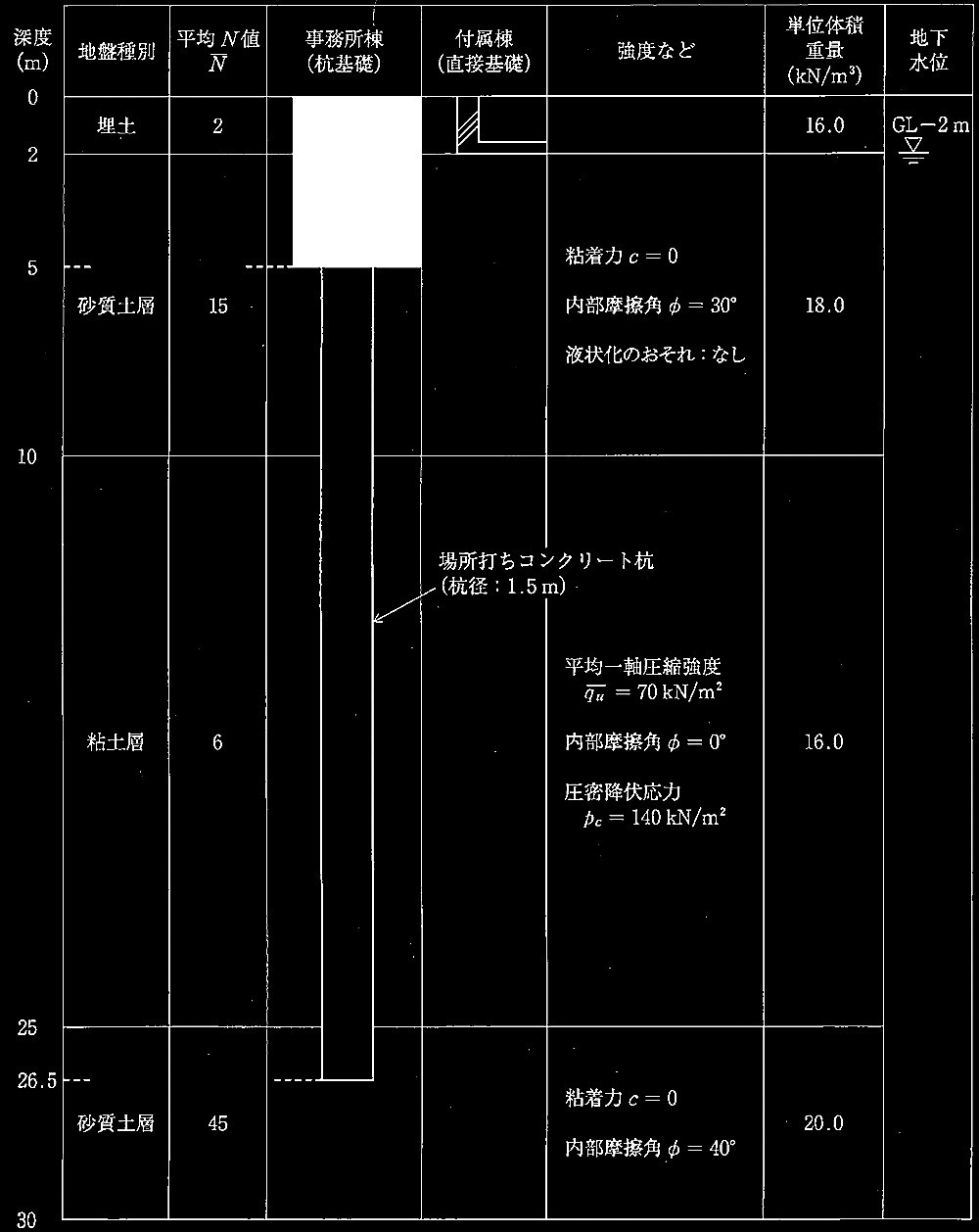
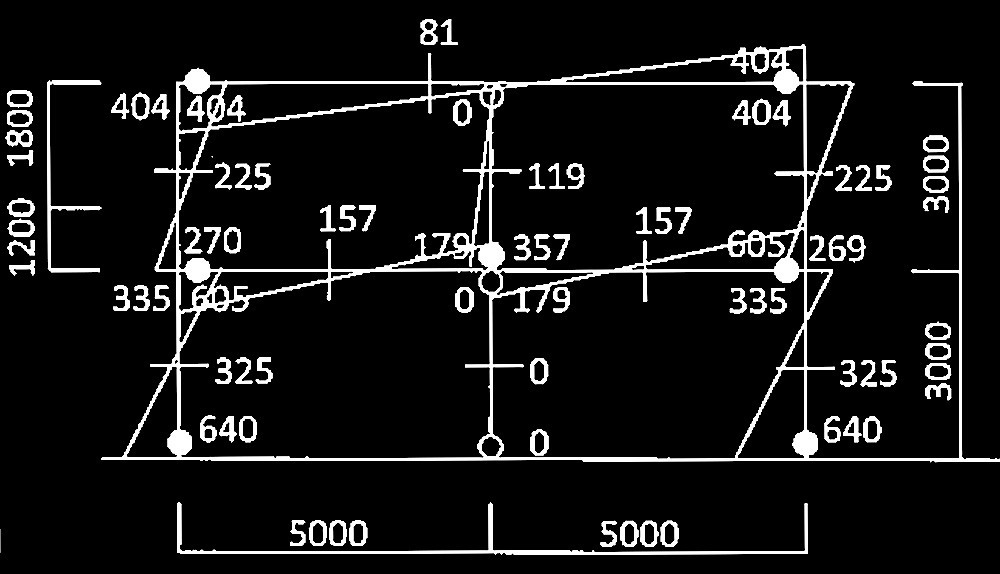
図1 地盤概要
[ No.1 ]
事務所棟の基礎形式は杭基礎を採用し、GL-25m以深に現れる砂質土層を支持層と想定して、以下のような杭の条件を設定した。次の?@〜?Bの設問に解答せよ。
<杭の種類> 場所打ちコンクリート杭(直杭)
<杭 径> 1.5m
<杭 長> 21.5m(杭先端深さGL-26.5m)
く基礎スラブ深さ> GL-5m
?@ 当該杭の1本当たりの極限先端支持力R p を式(1)より求めよ。

答え
[ 解答解説 ]
※数字の有効数字について、答えは3桁で表し、途中の計算も3桁で行った。最終桁の丸め方は四捨五入している。
?@ 平均N値:N =45
杭の先端支持力度 :q p
= 120・N
= 120・45 = 5400 (kN/m 2
)
杭 径:d = 1.5 (m)
杭先端の閉塞断面積:
A =πd 2
/4 = 3.142・1.5 2
/4 =1.77 (m 2
)
以上より、極限先端支持力R p
は式(1)より以下となる。
R p
= q p
・A= 5400・1.77 = 9558 → 9560(kN)
?A 当該杭の1本当たりの極限周面抵抗力Rfを式(2)より求めよ。ただし、杭先端の根入れ部分の周面抵抗力は無視するものとする。

答え
[ 解答解説 ]
砂質土部分の N値平均値:
N s
= 15
砂質土部分の周面抵抗力度:
τ s
= 3.3・N s
= 3.3・15 = 49.5 (kN/m 2
)
砂質土部分の長さ:
L s
= 5(m)
粘性土部分の周面抵抗力度:
τ c
= c u
= q u
/2 = 70/2 = 35.0 (kN/m 2
)
粘性土部分の長さ:
L c
= 15 (m)
杭の周長:
φ = π d = 3.142・1.5 = 4.71 (m)
砂質土部分の周面抵抗力:
R fs
=τ s
・ L s
・φ = 49.5・5・4.71 = 1170 (kN)
粘性土部分の周面抵抗力:
R fc
= τ c
・L c
・φ = 35・15・4.71 = 2470 (kN)
以上より、極限周面抵抗力R f
は式(2)より以下となる。
R f
= R fs
+ R fc
= 1170 + 2470 = 3640 (kN)
?B ?@及び?A で求めたRp及びRfを用いて、当該杭の1本当たりの長期許容鉛直支持力Raを求めよ。ただし、杭の自重は考慮しないものとする。
答え
[ 解答解説 ]
長期許容鉛直支持力R a
は極限先端支持力R p
及び極限周面抵抗力R f
より、以下となる。
R a
=( R p
+ R f
)/3 = (9560 + 3640)/3 = 4400 (kN)
[ No.2 ]
付属棟の基礎形式は直接基礎(べた基礎)を採用し、GL−2m以深に現れる砂質土層を支持層と想定して、以下のような条件を設定した。次の?@〜?Cの設問に解答せよ。
く基礎形式>
直接基礎(べた基礎:基礎底面 B × L=10m × 30m)
基礎の平均鉛直荷重度:40kN/m 2
く基礎荷重状況と地盤概要> 図2参照
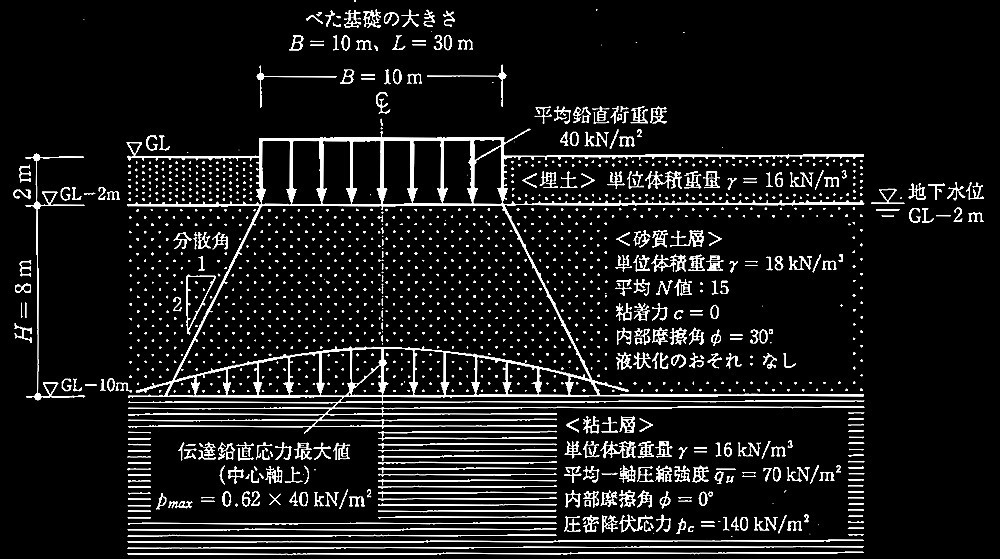
図2 基礎荷重状況と地盤概要
?@基礎直下の砂質土層の長期許容鉛直支持力度 q a1 を、式(3)を用いて求めよ。ただし、根入れ深さD f には埋土は考慮しないものとする。

表 支持力係数

答え
[ 解答解説 ]
※数字の有効数字について、答えは3桁で表し、途中の計算も3桁で行った。最終桁の丸め方は四捨五入している。
基礎の形状係数:
α= 1.0 + 0.2・B/L =1.0 + 0.2・10/30 = 1.07
基礎の形状係数:
β = 0.5 – 0.2・B/L = 0.5 - 0.2・10/30 = 0.433
支持力係数(φ = 30°):
N c
= 30.1、N γ
= 15.7、N q
= 18.4
支持地盤の粘着力:c = 0
支持地盤の単位体積董量:
γ 1
= 18 – 10 = 8 (kN/m 3
)
(地下水位以下のため水中単位体積重量)
根入れ部分の士の単位体積重量 :
γ 2
= 16 (kN/m 3
)
根入れ深さ:
D f
= 0 (m) (埋土は考慮しないため)
以上より、基礎直下の砂質土層の長期許容鉛直支持力度q α1
は式(3)より以下となる。
q α1
=(α・c・N c
+ β・γ 1
・B・N y
+ γ 2
・D f
・N q
)/3
= (1.07・0・30.1 + 0.433・8・10・15.7 + 16・0・18.4)/3
= 181 (kN/m 2
)
?A 直接基礎底面(GL-2m)に作用する鉛直荷重が、分散角1/2で粘土層表面(GL-10m)に(B + H)・( L + H )の大きさに均等に載荷されるものとして、直接基礎底面(GL-2m)に換算した粘土層の長期許容鉛直支持力度q α2 を、式(4)を用いて求めよ。ただし、根入れ深さD f は砂質土層厚Hとし、埋土は根入れ深さに考慮しないものとする。

答え
[ 解答解説 ]
基礎の形状係数:
α= 1.0 + 0.2・(B + H)/(L + H)
= 1.0 + 0.2・(10+ 8)/(30+ 8)
= 1.10
基礎の形状係数:
β= 0.5 – 0.2・(B + H)/(L + H)
= 0.5 – 0.2・(10+ 8)/(30+ 8)
= 0.405
支持力係数(φ =0°):
N c
= 5.1、N γ
= 0.0、N q
= 1.0
支持地盤の粘着力:
c =q u
/2 = 70/2 = 35 (kN/m 2
)
支持地盤の単位体積重量:
γ 1
= 16 – 10 = 6 (kN/m 3
)
(地下水位以下のため水中単位体積重量)
根入れ部分の土の単位体積重量:
γ 2
= 18 –10 = 8 (kN/m 3
)
(地下水位以下のため水中単位体積重量)
根入れ深さ:D f
= H = 8 (m)
以上より、直接基礎底面(GL-2m)に換算した粘土層の長期許容支持力度q α2
は式(4)より以下となる。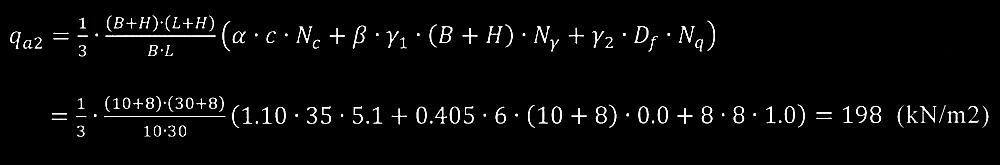
く参考>
通常、基礎底から存在している砂質土層下の2層地盤としての粘土層の許容支持力から砂質土層の重量を引く必要があり学会基礎指針2019に準拠して算出する。粘土層の長期許容支持力度q’ α2
は式(3)より以下となる。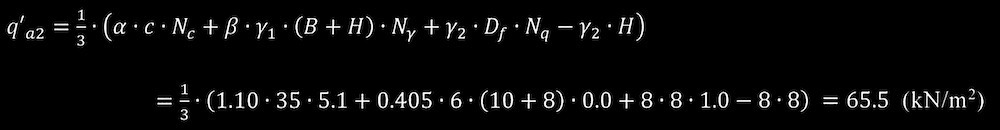
粘土層の長期許容支持力度q'a2から直接基礎底面(GL-2m)に換算した粘土層の長期許容支持力度q a2
は以下となる。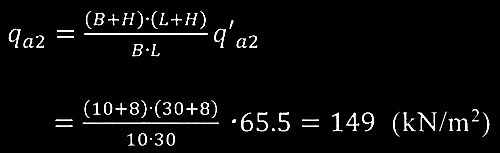
?B 圧密沈下が発生するか否かを計算により判定せよ。ただし、基礎の鉛直荷重度による粘土層の上面(GL-10m)の中心軸上の伝達鉛直応力の最大値P max は、図2に示すように 0.62 × 40 kN/m 2 とする。圧密沈下の検討では埋土の重量も考慮するものとする。
答え
[ 解答解説 ]
埋土の重量:
wb =γ・2 =16・2 = 32.0 (kN/m 2
)
砂質土層の重量:
w s
= (γ − 10) ・H = (18 − 10)・8 = 64.0 (kN/m 2
)
伝達鉛直応力の最大値:
P max
= 0.62 × (40 − 32) = 4.96 (kN/m 2
)
粘土層にかかる最大荷重:
P d
= w b
+ w s
+ p max
= 32.0 + 64.0 + 4.96 = 101 (kN/m 2
)
くPc= 140 (kN/m 2
)
以上より、粘土層にかかる最大荷重pdは101kN/m 2
であり、粘士層の圧密降伏応力度
p c
= 140kN/m 2
未満であるため、圧密沈下は発生しない。
?C 以上の?@〜?Bの検討より、本付属棟を図2に示すような直接基礎(べた基礎)で設計することが可能か否かを判断せよ。あわせて、その理由を述べよ。
答え
[ 解答解説 ]
基礎直下の砂質土層の長期許容鉛直支持力度q α1
は181kN/m 2
、直接基礎底面(GL-2m)に換算した粘土層の長期許容支持力度q α2
は198kN/m 2
であり、直接基礎底面の長期許容鉛直支持力度q α
は両者を比較して小さい方を採用し、181kN/m 2
となる。基礎の平均鉛直荷重度は40kN/m 2
であり、長期許容鉛直支持力度以下である。?Bの検討により、圧密沈下も発生しない。以上より、基礎の構造安全性に問題はなく、本付属棟を直接基礎(べた基礎)で設計することが可能である。