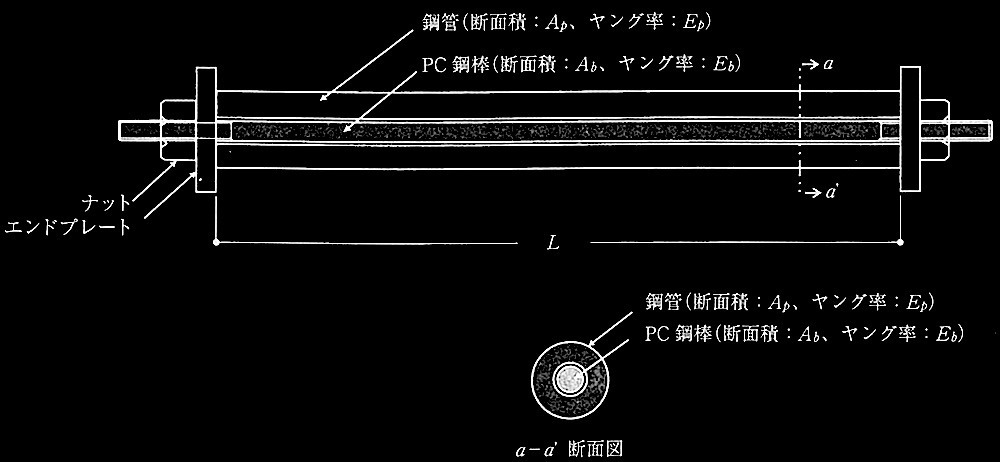
問題3
鉄筋コンクリート造の3棟の建築物を対象として、耐震計算ルート3により静的荷重増分弾塑性解析(以下、「増分解析」という)を実施し、保有水平耐力を確認した。次の[ No.1 ]〜[ No.3 ]の設問について解答せよ。
[ No.1 ]
計算対象の建築物は、 5階建て鉄筋コンクリート造耐力壁付きラーメン構造である。以下の ?@〜?Dの設問について解答せよ。なお、解答に用いる建築物の地震力算定用諸元を表1に、増分解析の条件及び解析結果を表2に示す。
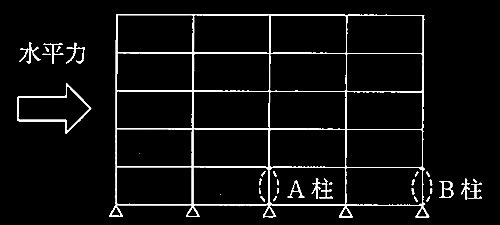
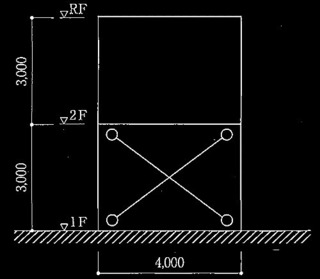
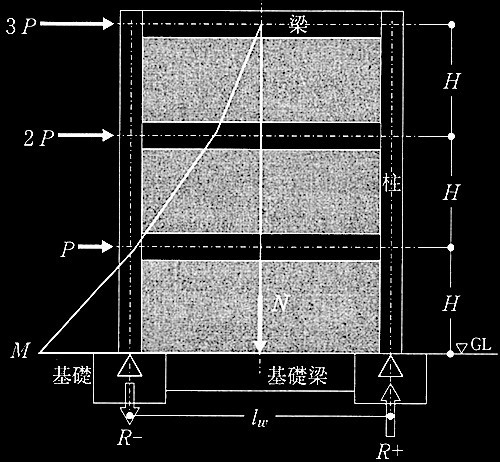
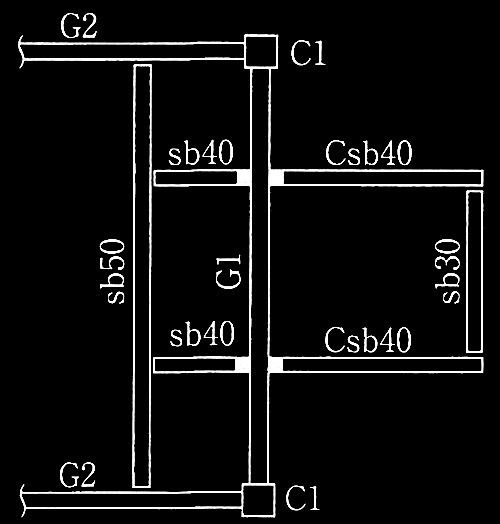
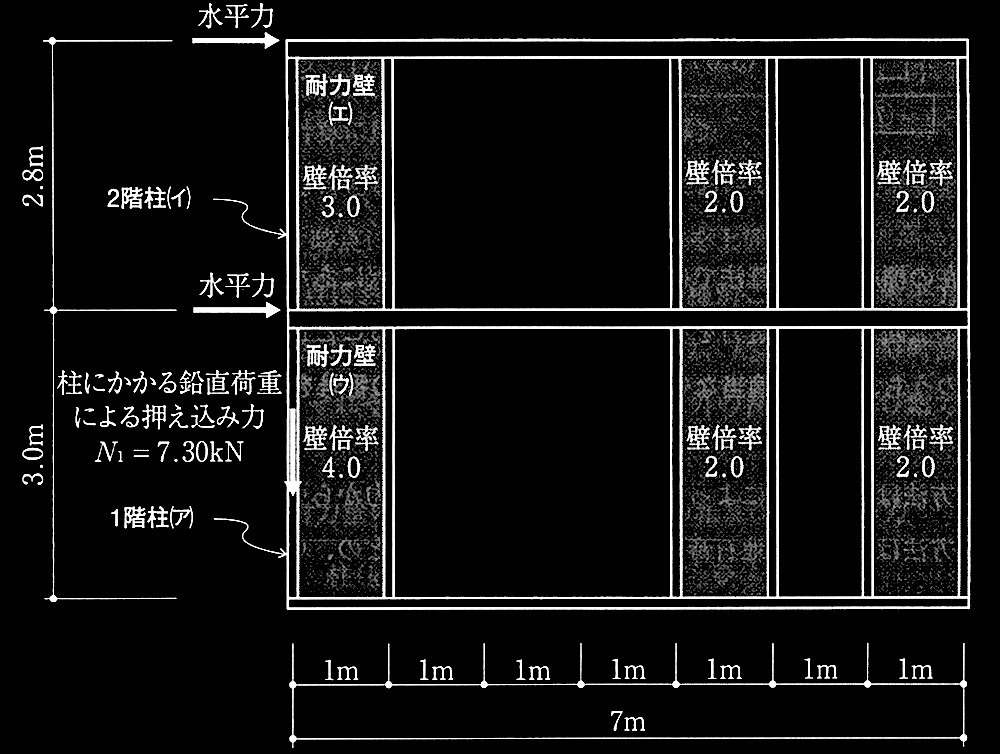
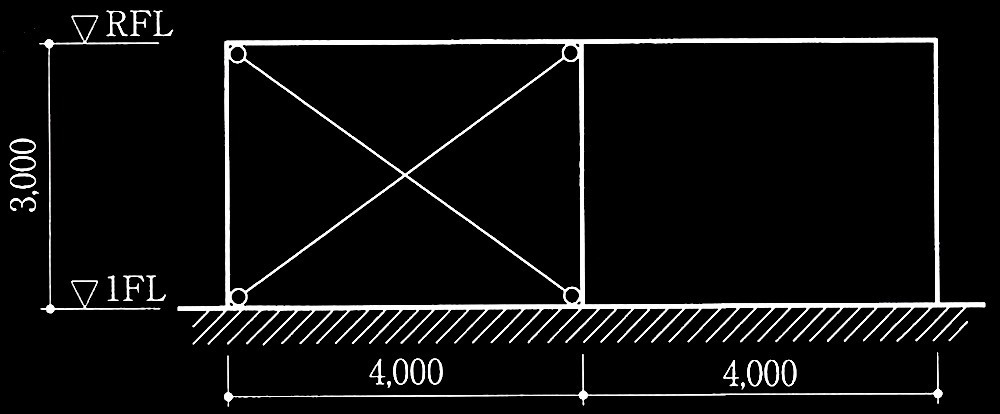
図1 架構とA柱•B柱(耐力壁は他の架構にある)
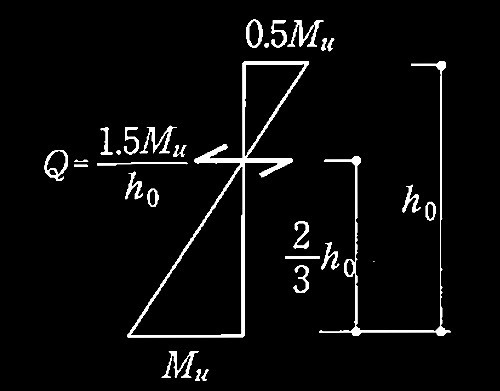
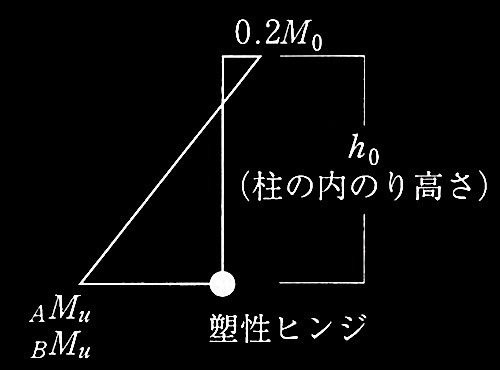
図3 1階柱の曲げモーメント分布
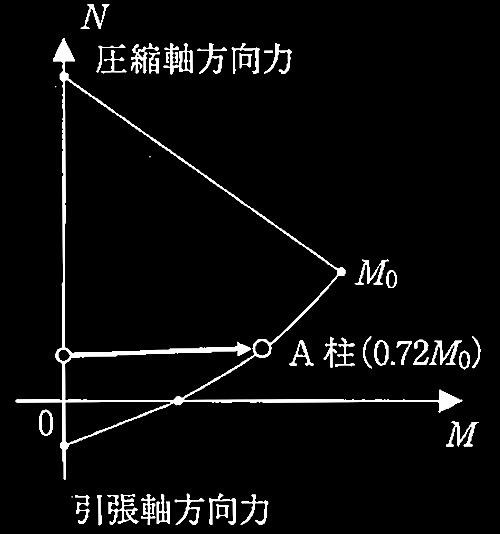
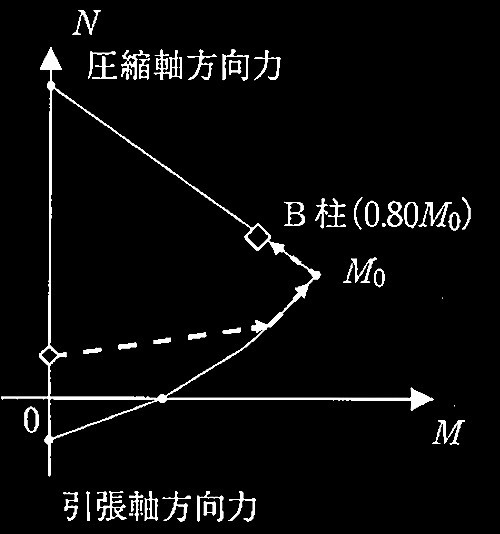
図2 柱の軸方向力(N)と曲げモーメント(M)との関係
表1 対象建築物の地震力算定用諸元
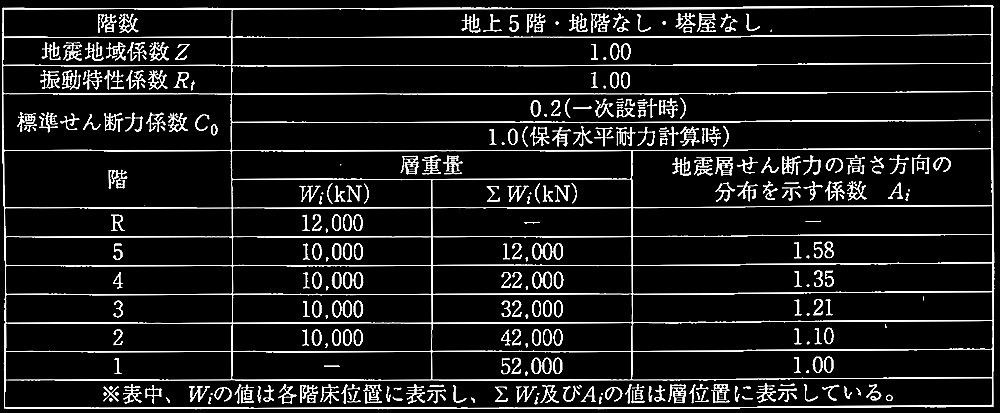
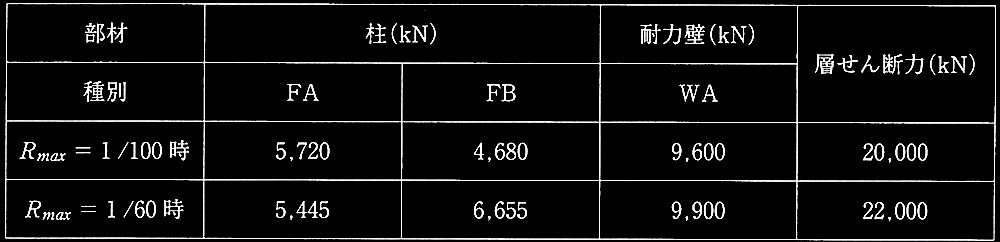
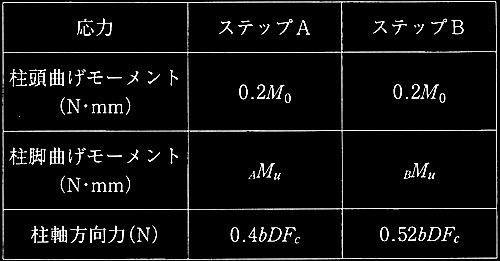
表2 増分解析の条件及び解析結果
(b) 増分解析では、柱の軸方向力N 曲げ終局モーメントMuとの相関関係(N-Mu関係)を考慮した。
1階におけるA柱及びB柱の N-Mu関係を図2に示す(圧縮軸方向力を正、引張軸方向力を負とする)。図2には、 A柱及ひB柱の柱脚について、増分解析の各ステップにおける軌跡をそれぞれ示す。なお、図中の括弧内の値は増分解析終了時における柱脚の曲げ終局モーメントである。
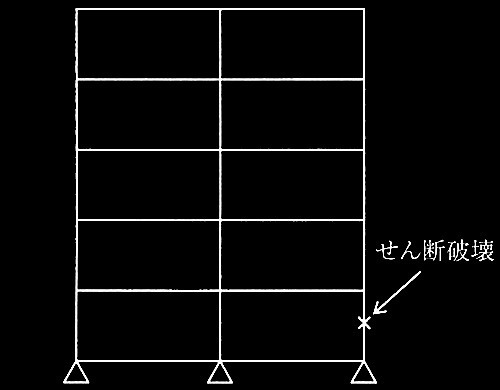
(c)増分解析終了時には、全体崩壊形を形成した。なお、1階柱脚は曲げ破壊したが、1階柱頭は曲げ破壊しなかった。
(d) 保有水平耐力は、増分解析終了時の水平耐力とした。
1 階の保有水平耐力は、 22,100kNであった。保有水平耐力時には、種別FAの柱が負担する水平耐力の合計が6,188kN、種別FBの柱が負担する水平耐力の合計が7,735kN、種別FCの柱が負担する水平耐力の合計が1,547kNであった。また、耐力壁群の種別はWAであり、耐力壁が負担する水平耐力の合計が6,630kNであった。
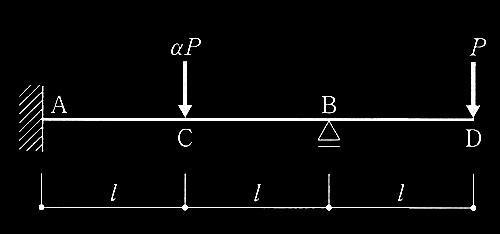
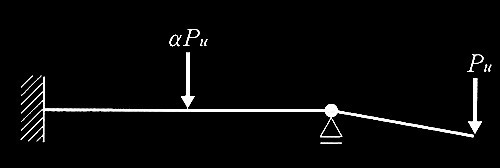
(e) 柱の破壊モードは、柱のせん断終局耐力Q su が式(1)を満足する場合には曲げ破壊、満足しない場合にはせん断破壊とする。ここでは、1階柱の柱脚塑性ヒンジ発生時せん断力 Q M は、式(2)による。その際、 1階柱の曲げモーメントの反曲点高さは 2/3ho(ho:柱の内法高さ)とする(図3)。
Q su ≧ 1.25 Q M ・・・式(1)
Q M = 1.5Mu/ho ・・・式(2)
?@ 5階の保有水平耐力Q u を求めよ。 Q u の単位はkNとし、小数第1位を四捨五入して表記せよ。
答え
[ 解答解説 ]
増分解析の水平力を一次設計用地震力の分布としているので、各階の保有水平耐力の比は 各階の一次設計用地震力の比と等しくなる。
一次設計用地震力は、表1の値を用いて、 Qi = Z・Rt・Ai・Co・ΣWi により求めるので、
1 階:Q 1
=1.00×1.00×1.00×0.2×52,000=10,400 kN
5 階:Q 5
=1.00×1.00×1.58×0.2×12,000= 3,792 kN
従って、 5階の保有水平耐力は、
Q u5
= Q u1
・Q 5
/Q 1
= 22,100 × 3,792/10,400 = 8058 kN
?A 1階のA柱及びB柱の破壊モードを曲げ破壊とするために必要なせん断終局耐力の下限値 min Q su について、下記の空欄に該当する数値を記入せよ。その際、柱のせん断終局耐力Q su は軸方向力の変動に関わらず一定としてよい。
A柱のせん断終局耐力の下限値
min Q su = [ ]Mo/ho
B柱のせん断終局耐力の下限値
min Q su = [ ]Mo/ho
答え
[ 解答解説 ]
1階柱の柱脚塑性ヒンジ発生時のせん断力 Q M
は式(2)により与えられ、破壊モードは式(1) を満足する場合に曲げ破壊とするので、破壊モードを曲げ破壊とするために必要なせん断 終局耐力の下限値は、
min
Q su
= 1.25Q M
= 1.25×1.5Mu/ho =1.875Mu/ho
図2より A柱及びB柱の増分解析終了時の曲げ終局モーメントMuが与えられているので、
これを上式に代入し、
A柱のせん断終局耐力の下限値
min
Q su
= 1.875×(0.72Mo)ho = 1.35Mo/ho
B柱のせん断終局耐力の下限値
min
Q su
=1.875×(0.80Mo)/ho = 1.50Mo/ho
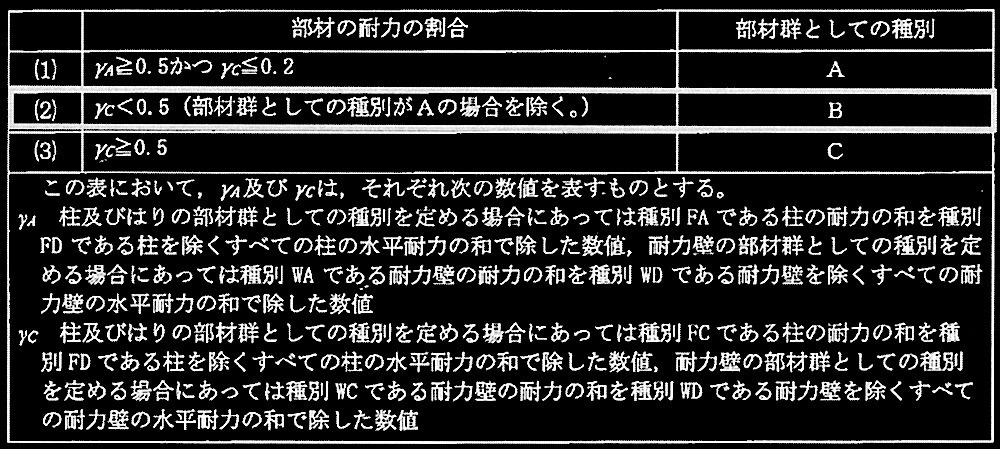
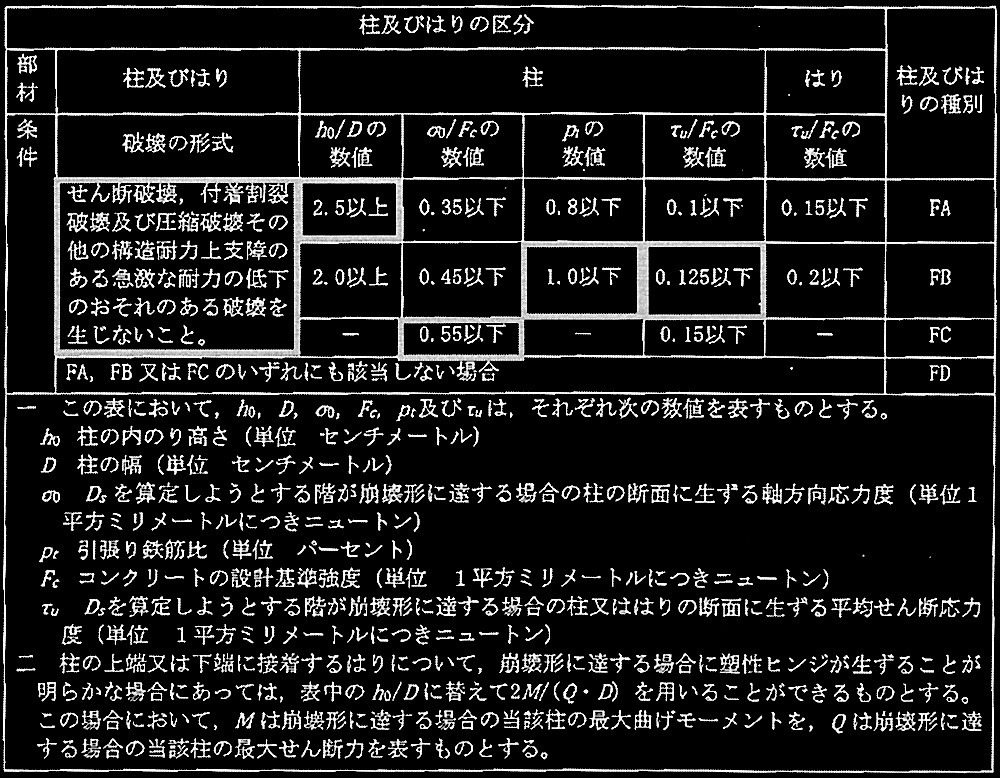
?B 1階柱の部材群の種別を昭和55年建設省告示第1792号第4に従って判定し、その種別及び判定理由を簡潔に記述せよ。
答え
[ 解答解説 ]
部材群の種別の判定は昭和55年建設省告示第 1792号第4第三号の表による。 各種別毎の1階の柱が負担する水平力は表2(d)の文中で与えられているので、
γ A
= 6,188/(6,188 + 7,735 + 1,547 ) =0.40
γ C
= 1,547/(6,188 + 7,735 + 1,547 ) =0.10
従って、 1階柱の部材群の種別は Bである。
判定理由:
γ A
= 0.40 < 0.5 のため A とはならず、γ C
= 0.10 < 0.5 により 1階柱の部材群の種別はB と判断できる。
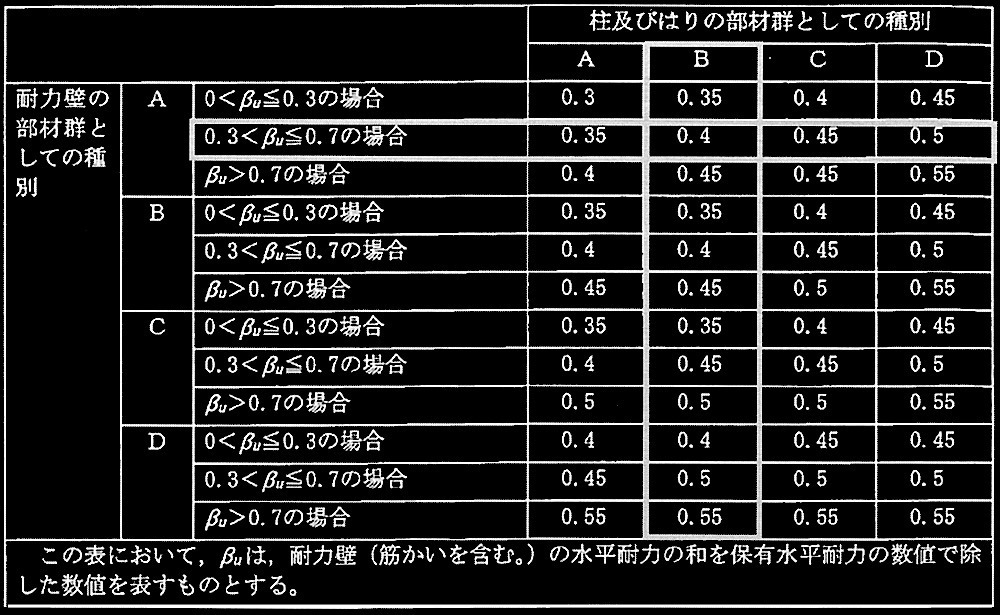
?C 1階の構造特性係数D s を昭和55年建設省告示第1792号第4に従って判定し、構造特性係数 D s 及び判定理由を簡潔に記述せよ。
答え
[ 解答解説 ]
検討建物は鉄筋コンクリート造耐力壁付きラーメン構造のため、 D s
の判定は昭和55年建設省告示第1792号第4第四号ハの表による。
1階の保有水平耐力 22,100 kN、耐力壁が負担する水平耐力の合計6,630kN、及び耐力壁群の種別WAは表2(d)の文中で与えられおり、耐力壁の水平耐力の分担率β u
は
β u
= 6,630/22,100 = 0.30
1階柱の部材群の種別は?Bの解答より Bとなる。
従って、 1階の構造特性係数はD s
= 0.35である。
判定理由:柱の部材群の種別はB、耐力壁の部材群の種別はWA、耐力壁の水平耐力の分担率 βu = 0.30 より D,=035 となる。
?D 1階の必要保有水平耐力 Q un は、20,020kNであった。1階の形状係数F es を求めよ。
答え
[ 解答解説 ]
必要保有水平耐力は Q un
= D s
・F es
・Q ud
で求められる。 ここで、Q un
= 20,020kN
Q ud
= 52,000 kN
D s
= 0.35
従って、
F es
= 20,020/(0.35 × 52,000) = 1.10
[ No.2 ]
表3の文章は、全体崩壊形の形成を設計目標とした、 14階建て鉄筋コンクリート造ラーメ ン構造の建築物に対して、増分解析により保有水平耐力を確認したときの構造設計者の所見である。この文章中の二重下線部分について、この対応が適切か、不適切かを答えよ。なお、不適切とした場合には、最も適切と考えられる対応を簡潔に記述せよ。
表3 対象建築物の構造設計者の所見
13階以上の階については解析終了時点の応力をそのまま用いて 、部材種別を判別し、各階の構造特性係数を算定した。
答え
[ 解答解説 ]
不適切
[最も適切と考えられる対応]
部材種別は、構造特性係数を算定しようとする階が崩壊形に達する場合の応力に基づき定めなけれぱならない。
本設問の建物のように増分解析において十分な変形まで至り、かつ変位増分に対して荷重増分が十分小さくなったが一部の部材に塑性ヒンジが生じず崩壊形が形成されない場合は、増分解析終了時の部材耐力に対する部材応力の比(部材応力/部材耐力)を用いて破壊形式を求め(余耐力法)、部材種別を判定し、構造特性係数を算定する。
[ No.3 ]
表4の文章は、直接基礎形式による 10階建て鉄筋コンクリート造連層耐力壁付きラーメン構造の建築物に対して、増分解析により保有水平耐力を確認したときの構造設計者の所見であ る。この文章中の二重下線部分について、この対応が適切か、不適切かを答えよ。なお、不適切とした場合には、最も適切と考えられる対応を簡潔に記述せよ。
表4 対象建築物の構造設計者の所見
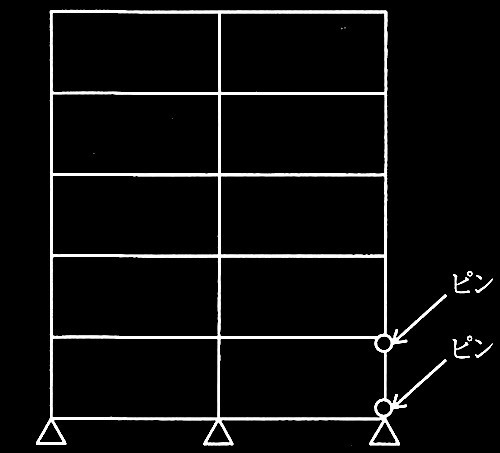
連層耐力壁は脚部の浮き上がりや沈み込みによる基礎回転形式の崩壊形として 、部材種別を判別し、
各階の構造特性係数を算定した。
答え
[ 解答解説 ]
不適切
[最も適切と考えられる対応]
連層耐力壁脚部の浮き上がりや沈み込みを許容した解析モデル(バネ支点モデル等)による増分解析では各階の構造特性係数が実際より小さく評価されることがあり望ましくない。
基礎をピン支点として連層耐力壁脚部の浮き上がりや沈み込みを拘東して増分解析を行い、部材種別を判別し、各階の構造特性係数の算定を行う。なお、この場合は保有水平耐力も浮き上がりや沈み込みを拘東した同じモデルで計算することとなる。
- no image